基于积分反步法的四旋翼飞行器轨迹跟踪控制

石 川

(四川理工学院自动化与信息工程学院，四川 自贡 643000)

基于积分反步法的四旋翼飞行器轨迹跟踪控制

石 川

(四川理工学院自动化与信息工程学院，四川 自贡 643000)

四旋翼飞行器的姿态动力学模型是多输入多输出(MIMO)、强耦合和非线性的。首先，对四旋翼飞行器动力学进行了数学建模。接着，提出了一种基于积分型的反步控制方法应用于四旋翼飞行器的稳定飞行及轨迹跟踪控制。通过引入跟踪误差的积分项，从而降低飞行器进行轨迹跟踪时的稳态误差。整个控制系统采用双闭环回路结构，内回路用于稳定飞行器的姿态角，而外回路用于控制飞行器的高度和水平方向的位移。最后，通过与传统的反步(Backstepping)控制法做实验对比，结果表明，应用积分反步(Integral Backstepping，IB)控制算法的飞行器能够较为精确地完成飞行器轨迹跟踪的任务。

积分反步；四旋翼飞行器；轨迹跟踪

引 言

四旋翼飞行器因其具有高度的机动性，且可以根据工作需求改变机身大小，成为了越来越受欢迎的研究平台[1]。为了执行各种任务，如对自然灾害的监视或军事监视，轨迹跟踪是四旋翼飞行器的基本功能。

反馈线性化方法[2-3]是为克服四旋翼飞行器的非线性和欠驱动而提出的。相较于自适应滑模控制器[2]，线性化反馈在嘈杂环境下显示出良好的效果。文献[3]提出了一种线性化H∞控制器，其对参数和扰动的不确定性具有鲁棒性。反步法[4-12](Backstepping)是以Lyapunov控制理论为基础，要求系统方程为严反馈形式，一种由前向后递推的设计方法。文献[13-15]分别将自适应控制方法和模糊控制方法与传统的反步控制相结合，使控制器更具鲁棒性与抗干扰性，从而更好地完成对飞行器的轨迹跟踪任务。

本文提出的积分反步法(Integral Backstepping，IB)，是在传统的反步法基础上添加了跟踪误差的积分项，以此来弥补稳态误差，用于控制飞行器稳定飞行及飞行器的轨迹跟踪。

1 四旋翼飞行器的建模

四旋翼飞行器的动态建模在很多方面得到了很好的解决。首先，定义飞行器的参考系。通常认为惯性坐标系固定于地球，即E(OE,X,Y,Z)。机体坐标系则是以飞控板为重心、以XYZ为轴向定义的，即B(OB,x,y,z)，如图1所示。

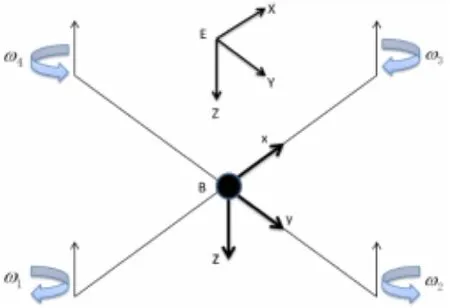
图1 四旋翼飞行器的参考坐标系

四旋翼飞行器可以看作是一个具有六个自由度和四个输入项的欠驱动的刚体，其动力学模型则是描述其空间姿态和位置信息的一个数学方程组。这四个输入项Ui(i=1,2,3,4)与四个电机的旋转角速度ωi(i=1,2,3,4)的关系为：

(1)

本文中，做出了如下假设：(1)结构体是呈刚性且对称的；(2)螺旋桨也是刚体；(3)电机的推力和阻力正比于转子转速的平方；(4)电机转动轴平行并平行于Z轴方向；(5)忽略地面效应；(6)惯性矩阵时不变；(7)忽略飞行器的弹性变形和所受冲击。

为了便于后续对飞行器的位置、航向、速度和角速度的研究。根据上述假设，通过Newton-Euler方程，可以获得飞行器的空气动力学方程：

(2)

其中，fB、τB分别是飞行器机体坐标系的外力和扭矩，I表示惯性矩阵，即：

(3)

图1中，机体主轴与机体坐标系坐标轴互相重合，所以式(3)改写成：

(4)

通过以上公式以及配置空间的运动方程[8]，可以针对四旋翼飞行器的线性运动和旋转运动进行数学建模。因为在惯性坐标系中，列写飞行器的线性运动方程式简单，而且在机体坐标系中列写飞行器的旋转运动方程也很方便，所以可以围绕飞行器的重心来表示旋转：

(5)

式中，ωd=ω4+ω2-ω1-ω3。

2 基于积分型的反步控制

2.1 四旋翼飞行器的状态方程

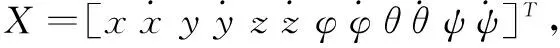
(6)

其中,

其中，Xi(i=1～12)分别对应状态向量X中的12个具体状态。

2.2 控制策略

四旋翼飞行器是一个强耦合、非线性以及欠驱动的系统。本文采用的控制策略如图2所示。

图2 控制流程结构图

2.3 控制器设计

本文采用的积分型反步控制法是在传统的反步控制[7-12]算法基础上引入跟踪误差的积分项，以此更好地消除稳态误差。

2.3.1 高度控制器

首先设计基于积分型的反步控制器的四轴飞行器高度位置控制器。

针对二阶系统：

(7)

首先，定义一个跟踪误差以及其积分项：

(8)

定义一个Lyapunov函数：

(9)

可以很明显看出V(K5,e5)≥0，即正定，对式(9)进行求导可得：

(10)

其中，f1是虚拟控制量，令

(11)

其次，定义一个二阶的跟踪误差：

(12)

则

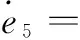
(13)

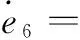
(14)

定义一个Lyapunov函数：

(15)

显然是正定的，同样求导可得：

(16)

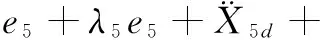
(17)

系统稳定。此时可得：

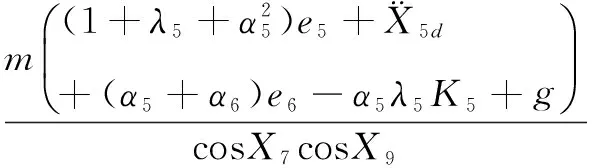
(18)

2.3.2 水平位置控制器

水平位置控制器分为X方向控制与Y方向控制，由于两者算法推导类似于Z方向。故这里只给出X与Y方向控制方法的结论：

(19)

(20)

其中

最后，通过反解模块就可将俯仰角和横滚角的期望值求出，即：

(21)

其中

2.3.3 姿态控制器

内环的姿态控制中，亦采用基于积分型的反步控制，且由于对俯仰角、航向角和横滚角的算法推导近似，故只列写俯仰角θ的推导公式。

假设二阶虚拟系统：

(22)

同理可定义并推导得：

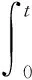
(23)

(24)

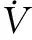
(25)

(26)

(27)

X8X12a3-X8a4ωd-b2U3

(28)

定义一个Lyapunov函数：

(29)

显然是正定的，求导可得：

(30)

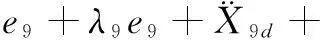
(31)

同理可知，该系统是稳定的。由式(31)可得：

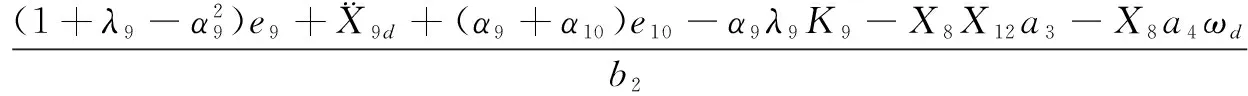
(32)

同理可得：

(33)

其中

最后通过式(1)反解并开方可得飞行器的四个电机的运转速度，即：

(34)

3 仿真与分析

本文实验仿真平台为MATLAB，程序以m文件的形式进行编写。四轴飞行器的相关物理参数见表1。为了验证本文控制算法的收敛性以及控制性能，设定的期望轨迹如式(35)，初始状态为：X=[012×1]。

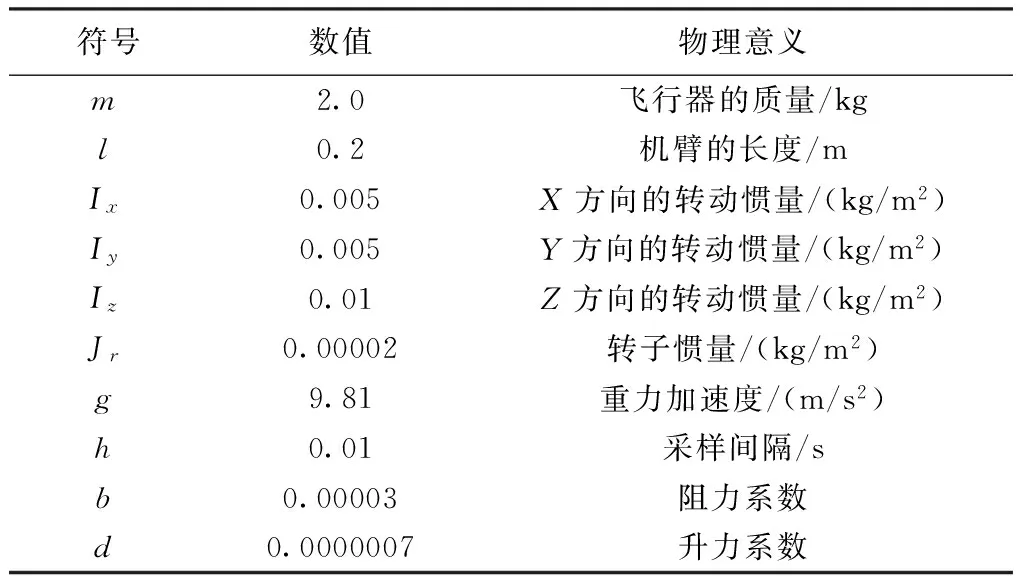
表1 四轴飞行器参数

(35)

经过反复调试，最终运用仿真参数见表2与表3。仿真结果如图3～图12所示。

表2 IB法仿真参数

表3 Backstepping法仿真参数

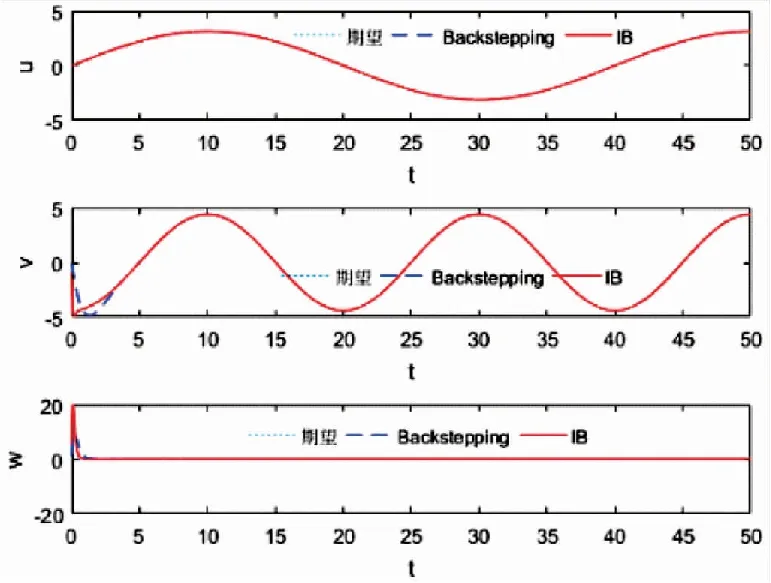
图3 飞行器的速度

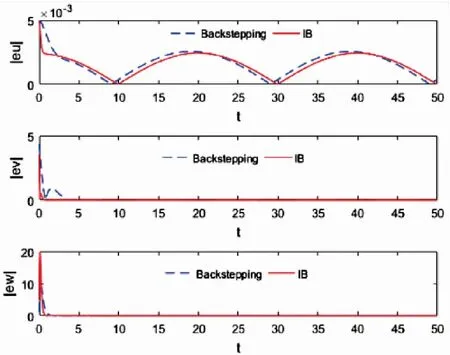
图4 飞行器的速度绝对误差

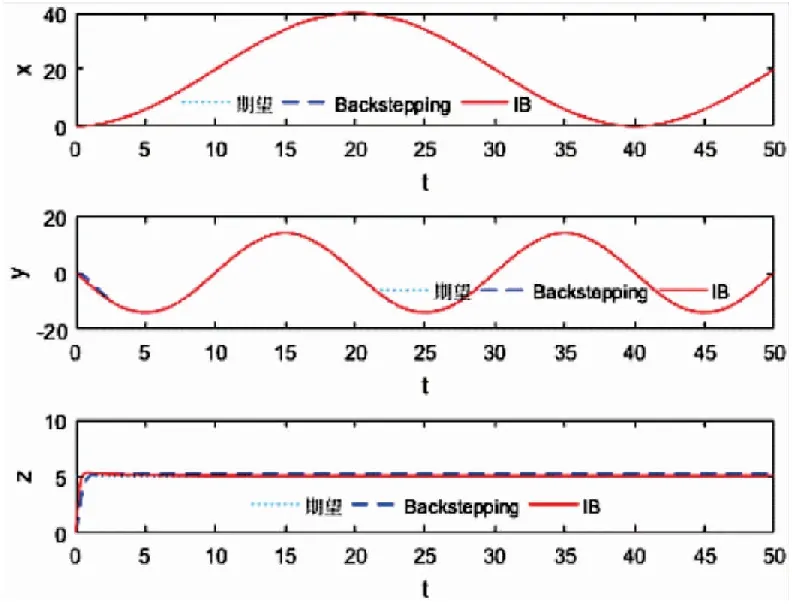
图5 飞行器的位置

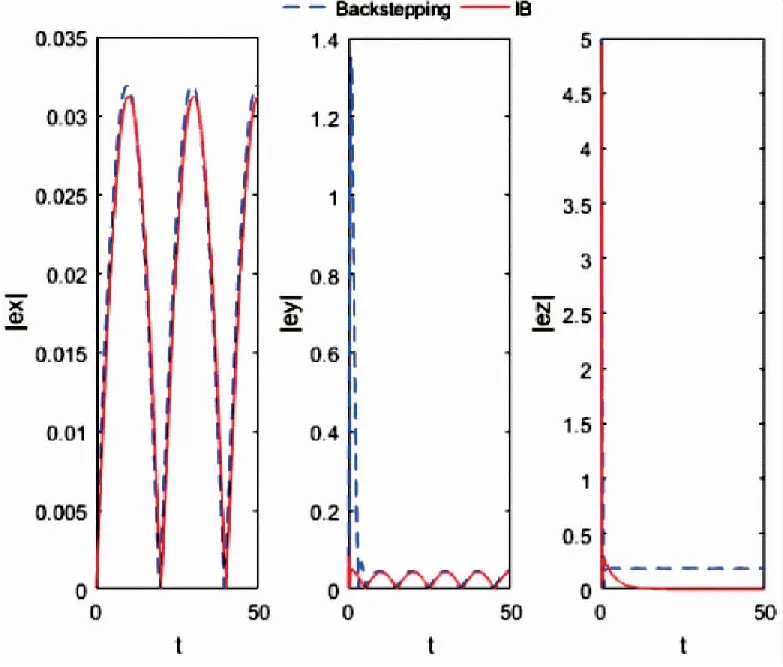
图6 飞行器的位置绝对误差

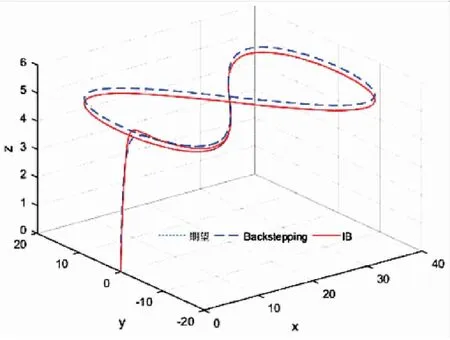
图7 三维轨迹

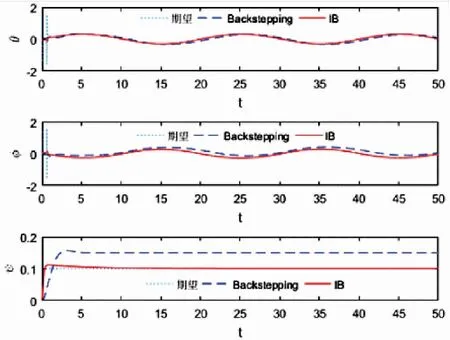
图8 飞行器的姿态角

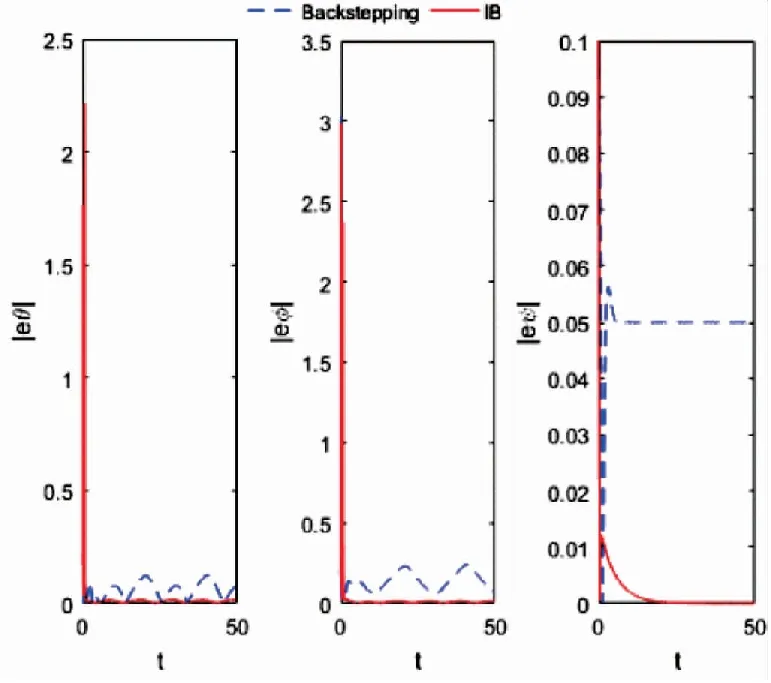
图9 飞行器的姿态角绝对误差

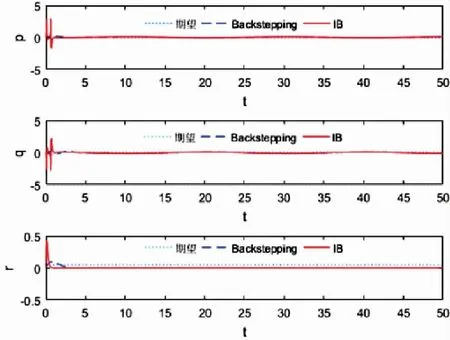
图10 飞行器的角速度

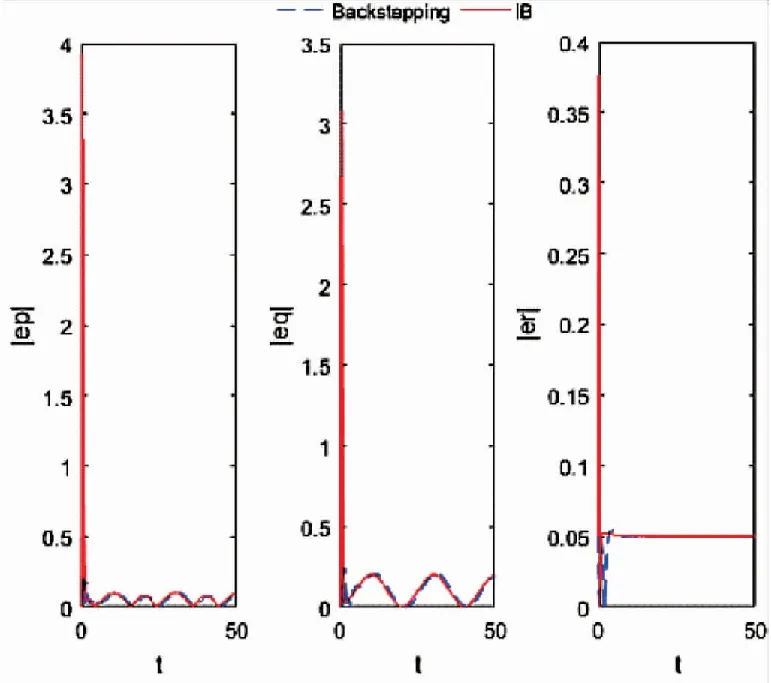
图11 飞行器的角速度绝对误差

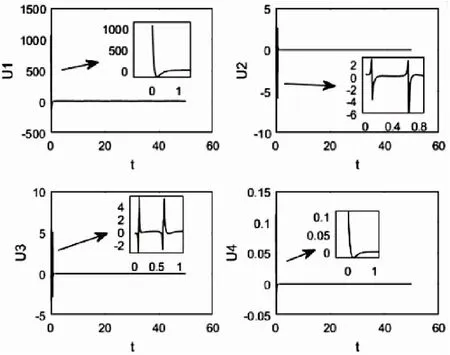
图12 飞行器的控制输入

从图5～图9可知，采用传统的Backstepping控制算法时的Z方向位置和航向角均存在一定的稳态误差，值分别为0.2和0.05，其余姿态角也存在小幅波动的稳态误差，而IB控制效果较为理想，无论是速度、位置还是姿态和角速度，跟踪的绝对误差极小，且保持在很小的范围内。图12给出飞行器的四个控制输入仿真图。实验证明，应用本文提出的IB控制算法的飞行器，飞行更加稳定，轨迹跟踪性更好。

4 结束语

本文提出的基于积分型的反步的控制算法应用于MIMO且呈非线性强耦合的四旋翼无人机飞行控制系统中，能有效减小稳态误差。通过与Backstepping算法进行实验比较，充分证明了系统收敛性好且稳定，稳态误差极小，控制效果较为理想，轨迹跟踪特性较强。后续工作将考虑阵风等外界干扰因素，对参数进行自适应调节，提高抗干扰性能与鲁棒性。

[1] KUMAR V,MICHAEL N.Opportunities and challenges with autonomous micro aerial vehicles[J].The International Journal of Robotics Research,2012,31(11):1279-1291.

[2] LEE D, KIM H J,SASTRY S.Feedback linearization vs. adaptive sliding mode control for a quadrotor helicopter[J].International Journal of control,Automation and systems,2009,7(3):419-428.

[3] Mokhtari A,Benallegue A,Daachi B.Robust feedback linearization and GH∞ controller for a quadrotor unmanned aerial vehicle[J].Journal of Electrical Engineering,2006,57(1):20-27.

[4] MATOUK D,GHEROUAT O,ABDESSEMED F,et al. Quadrotor position and attitude control via backstepping approach[C]//Proceedings of the 8th International Conference on Modelling,Identification and Control(ICMIC),Algiers,Algeria,September 15-17,2016:73-79.

[5] 王宏健,陈子印,贾鹤鸣,等.基于滤波反步法的欠驱动AUV 三维路径跟踪控制[J].自动化学报,2015,41(3):631-645.

[6] LU H,LIU C,COOMBES M,et al.Online optimisation-based backstepping control design with application to quadrotor[J].IET Control Theory & Applications,2016,10(14):1601-1611.

[7] BOUADI H,BOUCHOUCHA M,TADJINE M.Modelling and stabilizing control laws design based on backstepping for an UAV type-quadrotor[J].IFAC Proceedings Volumes,2007,40(15):245-250.

[8] YU Y L,JIANG C H J,WU H.Backstepping control of each channel for a quadrotor aerial robot[C]//Proceedings of 2010 International Conference on Computer,Mechatronics,Control and Electronic Engineering(CMCE),Changchun,August 24-26,2010:403-407.

[9] LEE H, KIM S,RYAN T,et al.Backstepping control on SE(3) of a micro quadrotor for stable trajectory tracking[C]//Proceedings of 2013 IEEE International Conference on Systems,Man,and Cybernetics(SMC 2013),Manchester,United Kingdom,October 13-16,2013:4522-4527.

[10] RASHAD R,ABOUDONIA A,ELBADAWY A.Backstepping trajectory tracking control of a quadrotor with disturbance rejection[C]//Proceedings of 2015 XXV International Conference on Information,Communication and Automation Technologies (ICAT),Sarajevo,Bosnia & Herzegovina,October 29-31,2015:1-7.

[11] ALTUG E,OSTROWSKI J P,MAHONY R.Control of a quadrotor helicopter using visual feedback[C]//Proceedings of 2002 IEEE International Conference on Robotics and Automation (ICRA'02),Wasington,D.C,May 11-15,2002:72-77.

[12] ASHFAQ A M,WANG D B.Modeling and backstepping-based nonlinear control strategy for a 6 DOF quadrotor helicopter[J].Chinese Journal of Aeronautics,2008,21(3):261-268.

[13] DONG Z,FAN H,WANG Y,et al.Adaptive backstepping controller design for quadrotor aircraft with unknown disturbance[C]//Proceedings of the 14th International Conference on Control,Automation,Robotics and Vision(ICARCV 2016),Phuket,Thailand,November 13-15,2016:1-5.

[14] YACEF F,BOUHALI O,HAMERLAIN M.Adaptive fuzzy tracking control of unmanned quadrotor via backstepping[C]//Proceedings of the 23rd International Symposium on Industrial Electronics (ISIE 2014),Istanbul,Turkey,June 1-4,2014:40-45.

[15] BASRI M A M,HUSAIN A R,DANAPALASINGAM K A.Fuzzy supervisory backstepping controller for stabilization of quadrotor unmanned aerial vehicle[C]//Proceedings of 5th International Conference on Intelligent and Advanced Systems (ICIAS 2014),Kuala Lumpur,June 3-5,2014:1-5.

Trajectory Tracking Control of Quadrotor Based on Integral Backstepping

SHIChuan

(School of Automation & Information Engineering, Sichuan University of Science & Engineering, Zigong 643000, China)

The attitude dynamics model of the quadrotor is multi-input multiple output (MIMO), strong coupling and nonlinear. The dynamics of quadrotor is modeled firstly. Then, a kind of backstepping control method based on integral type is proposed to apply the stable flight and trajectory tracking control to the quadrotor aircraft. By adopting the integral term of the tracking error, the steady-state error of the trajectory tracking is reduced. Double closed loop structure is used in the entire control system. The inner loop is used to stabilize the attitude angle of the aircraft, and the outer loop is used to control the height and horizontal displacement of the aircraft. Finally, by comparing with the traditional backstepping control method, the results show that the application of Integral Backstepping (IB) control algorithm can complete the task of vehicle trajectory tracking more accurately.

Integral Backstepping；quadrotor；trajectory tracking

2017-05-05

四川省教育厅自然科学重点基金(2016JY0179)

石 川(1992-),男,河北邯郸人,硕士生,主要从事无人机自适应控制方面的研究,(E-mail)1102sc@sina.cn

1673-1549(2017)04-0029-07

10.11863/j.suse.2017.04.06

TP242; TP391.9

A