静电场边值问题中唯一性定理的应用

郑 伟, 高天附

(沈阳师范大学 物理科学与技术学院, 沈阳 110034)

静电场边值问题中唯一性定理的应用

郑 伟, 高天附

(沈阳师范大学 物理科学与技术学院, 沈阳 110034)

在电磁场理论中,关于静电场边值问题的求解是重要而基本的。关于静电场边值问题的求解,在一般情况下可归结为在给定边界条件下求解场方程的问题,唯一性定理是求解静电场边值问题的理论基础。在电磁场相关课程中,静电场边值问题的求解都是教学中的重点和难点,但是作为判断场解正确性和唯一性的唯一性定理却经常被忽视。针对静电场边值问题的几种典型解法,以典型习题为例,深入分析了在各种解法中唯一性定理的应用及其重要意义,说明了在静电场边值问题中应用唯一性定理解题的思路和技巧。结合教学实践,指出了加强唯一性定理教学对于静态场教学的重要性,给出了关于唯一性定理教学的具体建议。

唯一性定理; 静电场; 边值问题

静电场的求解方法和特殊函数是动态电磁场的边值问题求解的基础,关于静电场的求解在电磁场理论中是重要而基础的。静电场求解问题可归结为在给定边界条件下求解场方程的问题,通常情况下可化为一定边值条件下解二阶偏微分方程的问题,一般统称为静电场边值问题。对于静电场边值问题已有许多解法,而其所得解是否唯一皆由唯一性定理[1]给出。静电场的唯一性定理是确立静电场有唯一正确解的标准,是关于求解静电场的各种方法的理论基础。

在相关电磁场理论课程的教学中,静电场的边值问题的求解是教学中的重点[2-6],同时也是教学难点,教师在教学中关注点多在具体的各种解法上,而学生在学习中对多种解法应接不暇,在教与学的过程中大多会忽略作为基础的唯一性定理。实际上,唯一性定理对于求解静电场边值问题有极其重要的指导意义,对唯一性定理的理解和应用常常在解决实际问题时有事半功倍的效果。本文从教学实践出发,针对静电场边值问题的常见解法进行分析,讨论唯一性定理在其中的重要应用,希望能为唯一性定理的教学提供一点思路。

1 唯一性定理

关于此定理的应用需注意:1)在满足唯一性定理的条件下,解是唯一的,但是不同情况下解的具体表述形式可以是不同的;2)区域的边界条件可以分为3种,第1类为Dirichlet边界条件即给定边界电势;第2类为Neumann边界条件即给定边界电势的法向导数;第3类为混合边界条件即已知一部分边界电势,已知一部分边界电势的法向导数[7-9]。

2 定理的应用

静电场的唯一性定理可以用来直接或间接求解静电场[10-13],如常用的试探法、镜像法求解静电场,而其他求解静电场的常规方法如分离变量法和格林函数法,在求解静电场时以解析法直接解场方程的方式得到场解,似乎无需用到唯一性定理,但实际求解时,唯一性定理的应用解决了所得解的正确性和唯一性的问题。以下以典型的静电场求解问题为例阐明定理的应用和重要性。

2.1 唯一性定理在镜像法中的应用

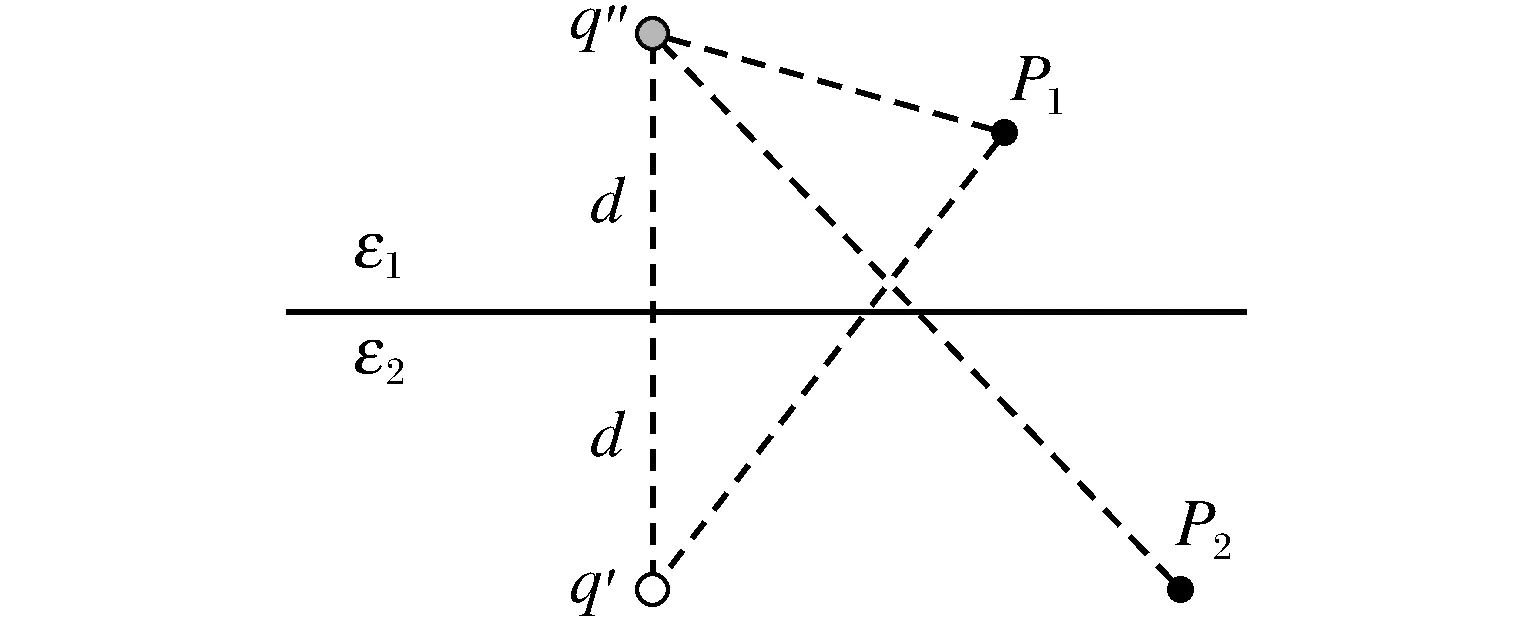
图1 镜像电荷设置示意图Fig.1 Schematic diagram of the setting for image charge

镜像法是求解静电场边值问题较为直观的方法。

典型习题1 在2种不同的均匀介质分界面的一侧有一自由电荷q,距界面距离为d,求空间的场。解此问题需选择直角坐标系。介质交界面处的边界条件为

如图1,在介质2和介质1中分别放置镜像电荷q′和q″,则两介质中的电势分别可以写为

将此解代入边界条件,可得

由以上求解过程并不能发现唯一性定理的应用,但此问题的解决唯一性定理起了非常重要的作用,分析如下:1)由题干可知,介质1中有一个点电荷,介质2中无自由电荷,由唯一性定理,即求解区域中自由电荷分布给定,故在介质1中电势满足泊松方程,在介质2中满足拉普拉斯方程;2)由题干可知,由于两种介质中只有一个自由点电荷,故区域有一边界条件为无穷远处电势为零;3)尝试解的点电荷表达式满足场方程和全部边界条件,由唯一性定理,此解是该问题的唯一正确的解。

在使用镜像法求解静电场时,镜像电荷的设置和场解的具体形式必须在满足唯一性定理的前提条件下提出,即镜像电荷不能放置在待求场区,否则影响场方程,解的形式除了满足介质交界面上的衔接条件外,还要满足其他边界处的条件,这样才能保证场解是唯一正确的。故唯一性定理的应用是镜像法解题的核心思想之一。在教学中要强调唯一性定理的思想,这样学生在学习镜像法的时候思路会更加明确,实际应用此解法时镜像电荷的设置和试探场解的提出才更加有的放矢。

2.2 唯一性定理在分离变量法中的应用

分离变量法是较为严格的数学解析求解场方程的方法。

典型习题2 在均匀外场E0中放一半径为R的的接地导体球,求空间的场。解此问题需选择球坐标系。考虑对称性球外电势φ的通解形式为勒让德函数

边界条件为

利用边界条件可得通解中的系数

故场解为

以上解题过程为利用分离变量法,结合边界条件,在球坐标系中解得最终结果。该解法表面看来不需要应用唯一性定理,仔细分析会发现唯一性定理的思想深入整个解题过程。分析如下:1)由题干可知,待求解区域中无自由电荷,满足拉普拉斯方程,故由对称性可以分离变量;2)由题干可知,此问题满足第一类边界条件,即已知边界处的电势;3)实际计算时代入边界条件的计算过程,只要对应系数相同即可,由此得到的解满足场方程和全部边界条件,由唯一性定理可知,是唯一正确的解,在计算时无需严格解析求解,大大简化了计算过程,降低了解题难度。

在使用分离变量法得到静电场场解的过程中,使用唯一性定理分析问题可以使解题思路明确,数学计算简化,场解的唯一正确性得到理论上的保证。在教学过程中,分离变量法较为严格的数学解析过程较容易为学生接受,故如果先由分离变量法开始,分析唯一性定理的应用思想,深入剖析问题的物理本质,进而尝试使用其他解法更容易令学生接受,在教学中会起到良好的效果。

2.3 应用唯一性定理直接求解静电场

试探法是直接应用唯一性定理求解静电场的方法。

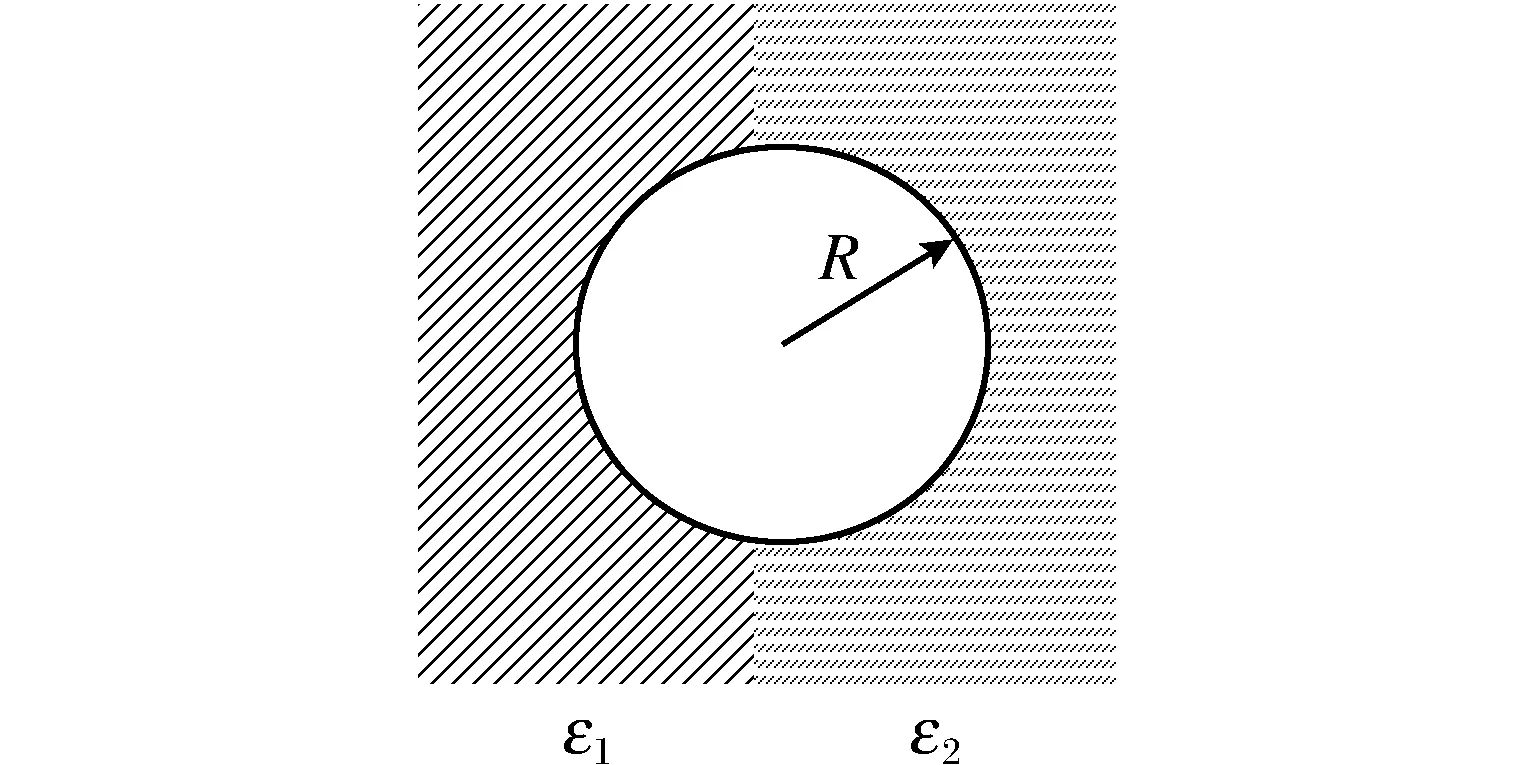
图2 位于介质中的带电圆柱Fig.2 Charged cylinder in the medium

典型习题3 如图2,一半径为R的无限长导体圆柱上均匀分布着电荷,电荷线密度为λ,柱外空间均匀充满两种介质。求空间电场。

分析空间电场可知,圆柱外空间的电场由均匀分布在圆柱体上的自由电荷和两介质中各自均匀分布的极化电荷共同激发,故柱外的电场具有柱对称性,方向沿柱坐标系中的er方向。故对柱外电场提出试探解:

边界条件为

由此边界条件可得场解为

验证可知,此解满足场方程和介质交界面处边值关系E1θ=E2θ, E1t=E2t,故为唯一正确的解。

前面例示的典型习题2也可以用试探法解题。分析该问题的物理实质,当该导体球置入均匀外场时,空间的电场由均匀外场和导体球上的感应电荷共同激发,导体球上的感应电荷分布具有对称性,相当于许多电偶极子。故对于球外电场提出尝试解:

其中前一项为均匀外场的电势,后一项为电偶极子的电势,此解必然满足泊松方程。同样可由边界条件得到场解的具体形式。可以发现,用试探法解此静电场问题比分离变量法更为方便,极大地简化了解题过程,很容易得到正确的场解。

试探法在静电场边值问题中的应用直接体现了唯一性定理在求解静电场时的重要意义和价值。表现为当静电场的场方程和边界条件确定时,无论通过何种途径得到的解,只要满足场方程和边界条件,所得解必为唯一正确的解。分析如下:1)提出适当的尝试解的形式满足场方程;2)场解的具体形式由边界条件决定;3)无需严谨的数学推导,得到的场解必是唯一正确的。

看似简单的试探法实际是教学中最难为学生掌握的一种方法,究其根本原因,一是因为在教学内容安排上,在讲述唯一性定理后马上安排试探法的教学,学生无法深入理解定理的深刻内涵,也就无法灵活应用;二是学生对静电场边值问题的物理本质分析不够透彻,无法提出合适的尝试解。鉴于这两点,在教学中更要注重唯一性定理的教学,重视对每一典型例题和习题引导学生深入把握唯一性定理的思想,逐步加深对定理的理解,从而达到熟练应用。

3 结 语

在教学中,任何一个教学难点都是教学研究中值得重视和深入思考的,静电场的唯一性定理的教学也不例外。对静电场的唯一性定理的认识不能仅仅局限于静电场的求解,定理的思想在求解静磁场时同样具有指导意义,因此对于定理的正确认识和深刻把握对于整个静态场求解都具有非常重要的意义,进而对动态电磁场的求解带来裨益。

建议在唯一性定理的实际教学时,教学重点放在定理的应用而非证明上,在教学内容的安排上,不仅单纯讲解定理,更要注重在静电场边值问题各种求解方法的教学中引导学生体会、运用唯一性定理的思想,进而在静磁场的边值问题时运用唯一性定理试探法解题,层层深入,使学生对该定理在思想上足够重视,运用上熟能生巧,从而达到真正掌握这一重要定理,在应用时发挥定理的应有作用。

[ 1 ]郭硕鸿. 电动力学[M]. 3版. 北京:高等教育出版社, 2008:43-46.

[ 2 ]李江芬. 如何在电动力学中讲解“惟一性定理”[J]. 中央民族大学学报, 2005,14(1):69-76.

[ 3 ]白卫峰,何伟,张勇. 基于Schur分解的比例边界有限元方法求解环形域静电场[J]. 四川大学学报(自然科学版), 2013,45(1):175-182.

[ 4 ]郑伟,吕嫣. 电动力学网络教学平台建设的研究[J]. 沈阳师范大学学报(自然科学版), 2013,31(4):531-534.

[ 5 ]钱林建,吴飞飞,邓平,等. 静电场的求解方法探讨[J]. 中国西部科技, 2013,12(4):121-124.

[ 6 ]黄煌. 用镜像法求解几类典型静电场问题的教学研究[J]. 湖南文理学院学报, 2013,25(1):68-73.

[ 7 ]尹真. 电动力学[M]. 3版. 北京:科学出版社, 2010,48-71.

[ 8 ]ROBERT R G, YANG T W．Electromagnetic Fields and Waves[M]. 北京:高等教育出版社, 2006:97-99.

[ 9 ]郑家奎. 三种描述类型静电场唯一性定理的证明[J]. 山东师范大学学报(自然科学版), 2003,18(1):110-112.

[10]肖峻,杨洪平. 电磁场的基本方程及其定解条件[J]. 电气电子教学学报, 2012,34(2):50-52.

[11]张婷玉,胡扬洋. 高师物理师范生电动力学学习困难的成因与对策[J]. 首都师范大学学报(自然科学版), 2015,36(6):30-34.

[12]张勇,林皋,刘俊,等. 静电场问题的等几何分析方法[J]. 大连理工大学学报, 2012,52(2):870-877.

[13]朱峰,成晟. 恒定磁场中镜像法叠加结果的矛盾分析[J]. 电气电子教学学报, 2015,37(6):53-54.

Application of uniqueness theorem in boundary value problem of electrostatic field

ZHENGWei,GAOTianfu

(College of Physical Science and Technology, Shenyang Normal University, Shenyang 110034, China)

The solution of the boundary value problem for electrostatic field is important and essential in the electromagnetic field theory. Normally, the solution comes down to the problem of solving the field equations based on the given borderline condition. Moreover, the uniqueness theorem is the theoretical basis for solving the boundary value problem of the electrostatic field. In the interrelated courses of electromagnetic field, the solution of the boundary value problem in electrostatic field is the key and difficult point for teaching. But the uniqueness theory, which is used to judge the correctness and uniqueness of the solution, is often ignored. This paper is aimed at several typical solutions of the boundary value problem in electrostatic field, for example, the application and significant meaning of the uniqueness theorem are analyzed in various solutions of typical exercises. Moreover, this article intends to explain the solution ideal and techniques for applying the uniqueness theorem in the boundary value problem of the electrostatic field. Based on the teaching practice, it points out the importance of uniqueness theorem in static field teaching, and gives some specific suggestions for the teaching of uniqueness theorem.

uniqueness theorem; electrostatic field; boundary value problem

2016-03-10。

辽宁省教育厅科学研究一般项目(L2014442)。

郑 伟(1975-),女(蒙古族),内蒙古赤峰人,沈阳师范大学讲师,硕士。

1673-5862(2017)03-0370-04

O442

A

10.3969/ j.issn.1673-5862.2017.03.022