非共识项目的立项决策研究

刘文波, 钮晓鸣

(1.同济大学,上海 200092； 2.上海新能源科技成果转化与产业促进中心，上海 200001；3.上海科学院，上海 201203； 4.上海产业技术研究院，上海 201203)

非共识项目的立项决策研究

刘文波1,2, 钮晓鸣3,4

(1.同济大学,上海 200092； 2.上海新能源科技成果转化与产业促进中心，上海 200001；3.上海科学院，上海 201203； 4.上海产业技术研究院，上海 201203)

非共识项目在初期难以达成一致意见，但由于存有潜在的创新价值，对非共识项目的研究越来越多，逐渐引发社会的广泛关注。从创新项目的特点以及管理上存在的问题入手，构建了模糊评价模型，用模糊评价的方式对非共识项目进行甄选，望能引起有关专家学者的指点和建议，以期对非共识项目的认识和管理日益完善。

非共识项目; 立项; 决策; 模糊评价

非共识项目通常是指具有较强的创新性，但在同行评议中多数评审专家认为不应当予以资助的申请项目[1]。针对这类非共识项目难以得到资助、但是又很有必要资助的问题，在立项决策问题上值得进行深入的研究探索。

1 非共识项目的特点

1.1 很高的不确定性和不可预测性

非共识项目因为创新性强，且与传统科技比较而言有很强的颠覆性，也就意味着非共识项目有很高的不确定性，或者说有很大的风险。这其中有技术的风险，技术能否达到预期的目标，同时创新往往涉及跨学科、跨团队等多要素组合，能否达到预期的效果，以及创新成功之后，能否达到预期的市场反应，这些都构成了创新的不确定性。中国本土企业康佳、TCL等都在20世纪90年代切入手机业务，但被后起之秀华为、小米等取代，这些创新路上后来者居上的案例，都是不可预测的。创新之路，不进则退，因为创新的不确定性和不可预测性，创新路上没有永远的王者，这也意味着只要我们坚持创新理念，我们面前就充满了希望。

1.2 有很强的颠覆性，且初期难以形成共识

非共识项目是一种颠覆性的全新行为，不仅涵盖思想文化创意，还包括各类创新资源的汇聚，以及技术层面的突破。或者可以说，创意已从经济学概念延伸到社会学概念。非共识项目还有一个很重要的特点就是初期可能不被广泛接受和认可。美国思科公司是斯坦福大学毕业的一对夫妇1984年创办的，当时需要投资的时候他们去找风投，找了72家风投没有一家愿意给钱，因为都不看好它，只是到了第73家才拿到一笔钱[2]。风险投资家是些非常聪明的人，削尖脑袋找有利可图的项目，但也经常眼拙！这意味着，如果选择73个专家评选这个项目，只有一个专家赞成，显然无法立项。阿里巴巴创始人马云创业初期怀揣商业设想却四处碰壁，正是处于创新创业初期，创新理念难以被多数人认可。同样的道理，如果按照我国现行的专家评审和行政审批制度，类似初创时期的阿里巴巴也是难以获得资助的。

2 目前存在的一些问题

2.1 缺乏针对颠覆性创新项目立项的非共识机制

发达国家已经探索了针对非共识项目的专用立项方式[2]，如美国国家科学基金会(NSF)和国立卫生研究院(NIH)经过十多年的探索，已形成了一套较为完善的评价制度和流程[1]。

目前，我国针对非共识项目缺乏有针对性的管理办法和实施细则，有不少非共识项目仍然混同于一般科研项目遴选，依然是职能部门交给专家遴选。专家遴选就是遵循少数服从多数的规则，在这种遴选决策机制下错失创新项目的案例并不鲜见，创新项目在最困难时候如果得不到雪中送炭的支持，就可能悄无声息地夭折。

2.2 对体制内鼓励扶持创新的主体缺乏激励

美国国家科学基金会(NSF)和国立卫生研究院(NIH)针对非共识项目的立项有不少都由主管的行政官员决策立项，他们立项前与申请者进行充分的交流沟通，同行评议的意见仅仅作为参考。比较而言，我们对行政官员在决策非共识项目成功时的激励以及失败时的宽容还不够。这里所提鼓励创新、宽容失败，指管理方面的创新，是针对体制内决策创新、配置资源的执行者，包括相关职能的政府官员、国企领导。

2.3 对创新性强的非共识项目缺乏有效的专用通道

一些科研项目的评审中，对创新性强或者说具备颠覆性的创新项目，在同行评议中如果因为综合成绩落选而未能立项，还缺乏进一步的评判通道。科学上，对真理的认识往往首先是从个别人开始，有个循序渐进被大众认可的过程。对创新性强的非共识项目在决策立项的过程中，非常有必要增加对话机制、复议机制、增加深入评审、数学定量分析等专用通道，以免错失有潜在重大价值的创新性强的非共识项目。

2.4 缺乏对非共识项目的数学方法定量分析研究

由于非共识项目在专家评议过程中，有人说好有人说坏，在此过程中，有必要用数学的方法深入分析。比如，对非共识项目重点分析创新性，增加综合评判的权重，对对立的评审意见建立数学模型，分析其对立的数学性质，筛选出潜在的有价值且创新强的非共识项目，本文利用模糊评价方法引入数据离散度分析进行探索。

3 模糊评价模型构建

综合评判分析是一个复杂过程，研究方法甚多，应用极其广泛[3]。由于模糊决策方式在概念与运算上更贴近人的思维过程，故模糊综合评判方法在实际应用中被大量采纳[4]。然而，无论哪种评判方式都涉及人的参与，主观因素不可避免地会出现在评判过程中，或多或少地会影响到最终的评判结果。通过方差分析，引入“数据离散度”因子表征各评判者之间判断结果的差异性，经综合后作为一个重要的人为因素指标与综合评判结果配对，以进一步提供决策信息。通过均方差与“最大均方差”之间的分析比对，提出数据离散度是否可接受的一个判据。数据离散度分析可作为筛选“非共识性项目”的一种方法。

3.1 模糊综合评判模型

设评判对象(项目)为P：其中评判因素集U={u1,u2,…,un},评判指标集V={v1,v2,…,vm}。评判者s，s=1,2,…k，对U中的每个元素ui，i=1,2,…,n,对照V中每个指标vj，j=1,2,…,m，作一次评判得评判系数rij。如果ui选中vj则rij=1，其余为0。rij可看作ui相对于vj的“隶属度”。取遍ui，vj，i=1,2,…,n，j=1,2,…,m，得评判矩阵：

(1)

(U，V，Rs)构成评判者s的一个模糊评判模型。如有k个评判者，则评判矩阵为：

(2)

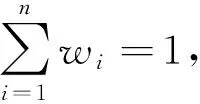
AA=W·R={a1,a2,…,am}

(3)

归一化得A={a1,a2,…,am}。按最大隶属度原则，对照评判集V，便可确定评判对象P的评价指标。

确定权重的方法一般可采用集值迭代法或层次分析法(AHP)[3,5]。式(3)中的运算一般可采用(×，+)或(∧，∨)等方式。

3.2 数据离散度的确定与分析

一般而言，评判指标集V中的每个元素vj，j=1,2,…,m，都是由语言或字符表达，如“优、良、中、差”“A，B，C，D”等。为对V作出定量描述，可将V在实轴上作反向投影。不失一般性，假设V在实轴上的反向投影落在[0，10]区间中。将[0，10]作m-1次划分，形成m个子区间，使得vm落在第一个子区间中，vm-1落在第2个子区间中，依次类推，v1落在第m个子区间中。在实际应用中可将[0，10]作m个等分子区间。将vj转化成三角模糊数表达，按最大隶属度取vj所在子区间的中值对vj进行表征。如当m=5时，5个子区间分别为[0，2]、[2，4]、[4，6]、[6，8]、[8，10]，v2=7、v5=1，如图1所示。

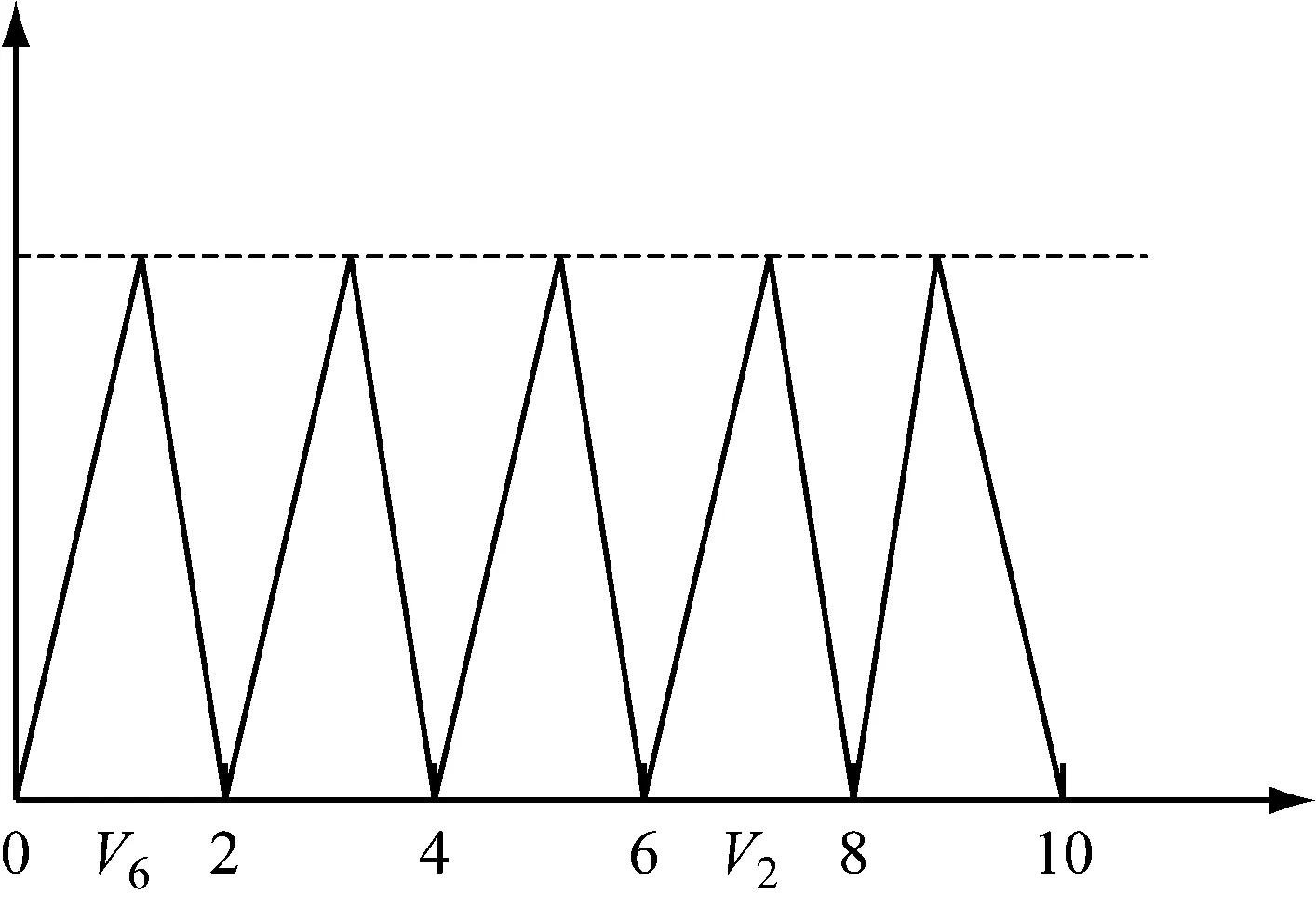
图1 用三角模糊数对vj进行表征

当k个评判者随机挑选并分别独立评判时，vj，j=1,2，…,m，为随机变量，式(2)中的元素，在不混淆的前提下为方便起见仍记为rij，表示第i次试验中vj出现的概率。故期望值为：

(4)

均方差为：

(5)

i=1,2,…,n

定义1 当U，V确定后，均方差σi(V)表示k个评判者就评判因素ui相对于V作出评判的数据离散度。

对式(5)作加权平均，则有

(6)

定义2 当U，V确定后，σ(V)称为总均方差，表示k个评判者就U相对于V作出评判的数据总离散度。

显然，σ(V)越小，数据越集中，反之数据越分散。σ(V)多大会超出接受程度是一个值得深入研究的问题。当U，V确定后，vj，j=1,2,…,m，可通过[0，10]中的数值唯一表征。因此，对每个ui存在最大均方差，即maxσi(V)，i=1,2,…,n。显然，总的最大均方差maxσ(V)=maxσi(V)。如，当=5时，对[1，10]作5等分，分别有v1=9、v2=7、v3=5、v4=3、v5=1。当k为偶数且评判值取两个极端v1和v5，容易算得maxσ(V)=4。

通过大量实例比对试验研究，本文给出判据如下：

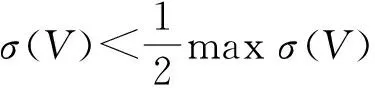
当数据离散度超出阈值，可考虑采用增设评判者等方式对P进行重新评估，也可将P作为“非共识性项目”进行处理。

4 案例应用与分析

设由15名专家参与对某科研项目P1和P2的综合评价，为项目立项进行论证。建立项目P1、P2的评判因素集U如下：

u1-技术和产品的先进性分析；

u2-项目中涉及的关键技术及工艺的创新性；

u3-技术工艺路线和相关制造标准的可行性；

u4-产品的市场容量和产业化前景；

u5-投入产出比分析和财务预算情况；

u6-承担项目的基础条件状况。

确定评价指标集V={v1,v2,…,v5}如下：

V={好，较好，一般，较差，差}

(7)

本例采用集值迭代法确定权重W。事先邀请5名专家相互独立地从因素集U中挑选出4个被认为最重要的因素组成因素子集，依次为

U1={u1,u2,u3,u4}

(8)

U2={u2,u3,u4,u5}

(9)

U3={u2,u3,u5,u6}

(10)

U4={u2,u4,u5,u6}

(11)

U5={u1,u2,u4,u6}

(12)

由式(8)～(12)可以看出u1～u6被选中的次数分别为2，5，3，4，3，3。归一化得

W={0.1,0.25,0.15,0.2,0.15,0.15}

(13)

由上述讨论可确定V的反向投影区间及表征值，即v1=9、v2=7、v3=5、v4=3、v5=1。

统计15名专家对P1、P2的评判票数得评判矩阵R1，R2如下：

(14)

(15)

式中，R1，R2中的rij代表第i个评判因素获得第j个评价指标的个数占比。例如：R1中的r23中的数字2/15，代表15个专家对评判因素u2投出“一般”票的有2个，在15个专家中占比2/15。

取(×，+)运算，得

归一化得

A1=0.437,0.367,0.124,0.054,0.018)

(16)

同理可得

A2=(0.287,0.186,0.088,0.128,0.311)

(17)

按最大隶属度原则，P1综合评价为“好”，P2综合评价为“差”。

进一步作数据离散度分析。容易算得P1的期望值和均方差分别为:

E1(V)=7.4,σ1(V)=1.81

E2(V)=6.9,σ2(V)=2.36

E3(V)=7.0,σ3(V)=1.79

E4(V)=7.8,σ4(V)=1.42

E5(V)=6.9,σ5(V)=1.86

E6(V)=8.2,σ6(V)=1.27

加权平均得

(18)

数据总体离散度可接受，评价者意见比较趋于一致。项目P1的最终评价为“好”。

同理，P2的期望值和均方差分别为:

E1(V)=5.9,σ1(V)=3.42

E2(V)=4.2,σ2(V)=3.49

E3(V)=4.7,σ3(V)=3.17

E4(V)=5.5,σ4(V)=3.38

E5(V)=5.4,σ5(V)=2.75

E6(V)=4.7,σ6(V)=2.91

加权平均得

(19)

数据总体离散度大，评判者意见相异性明显。虽然P2综合评价为“差”，但其专家评审意见中离散度较高，或者说专家评判的对立性较高，考虑到专家意见冲突，可建议考虑P2为“非共识性项目”，或增加评判者数量进行补充评议，以不错过创新性强的非共识项目。

综合评判过程中因各种原因必然会产生数据离散现象，甚至会产生对立的评判数据，这给决策带了困扰。一般取平均的做法有时不够严谨科学。例如有人说“好”,有人说“差”，中庸一下变成“一般”,往往会造成对问题的误判。本文提出了总均方差与最大均方差之间的比值作为衡量数据离散度大小的一个新判据，作为决策者评估最终结果的重要参考指标。如何优化总均方差与最大均方差之间的比值作为数据离散度可接受的阈值，有待进一步研究。

5 结束语

颠覆性创新项目初期可能未必能够被众人所认可，难以形成共识，这就引出如何从管理层面上设计好建立非共识项目的立项机制。通过建立对话机制或者复议方式，或者通过引入更多专家的多次评审，通过分析同行评议评审意见的数据离散度遴选，还可以专家署名的方式为非共识项目推荐。建立和完善主体责任和激励并重的机制，鼓励行政官员与非共识项目的申请者深入沟通交流，敢于负责任、敢于决策。

非共识项目在同行评议中，往往出现专家对立现象，如上述的P2项目由于专家评审中的对立意见较多，综合评审成绩低于P1而不能立项，在这种情况下，对他们的评审意见的数据离散度进行分析，发现P2的离散度较高，可能是潜在的非共识项目，有必要进一步增加数学定量方法的应用进行深入分析，或者增加评审专家再次评议。

出于不错过颠覆性创新项目的考虑，建立非共识项目立项机制，必须要同时引入动态管理，随时跟踪该创新项目的进展，如有偏差随时终止，如有进展则适时加大支持力度，这样的动态管理可以考虑由法人单位进行跟踪管理。其次，要引入社会监督与过程管理，对过程中发现的造假不诚信动态纠偏终止。另外，适时运用市场机制，引入资本关注，为创新主体提供条件并共担创新失败的风险。

[1] 黄鑫.NSF和NIH非共识项目选择和支持的经验和启示[J].科技发展研究,2010(6).

[2] 周光中.基于D-S证据理论的科学基金立项评估问题研究[J].2009.

[3] 郭亚军.综合评价理论与方法[M].北京:科学出版社，2002.

[4] 汪培庄.模糊集合论及其应用[M].上海:上海科学技术出版社，1983.

[5] SaatyT L.The Analytic Hierarchy Process[M].McGraw-Hill,1980.

Research on Non Consensus Porject Establishment and Decision-Making

LOUWenbo1,2,NIUXiaoming3,4

(1. Tongji University， Shanghai 200092, China; 2. Shanghai New Energy Center for Technology Transfer and Industry Promotion, Shanghai 200001, China; 3. Shanghai Academy of Science & Technology, Shanghai 201203, China; 4. Shanghai Industrial Technology Institute, Shanghai 201203, China)

It’s difficult for Non consensus project to reach consensus in initial stage. But for their potential innovative values, researches in Non consensus project are increasing quantitatively and drawing more and more social attention. This article starts with the properties of innovative programs and the problems in their management, elaborates on fuzzy evaluation model and utilizes the model to screen Non consensus project. Hope this article can attract the advice from relevant scholars and experts and help modify the knowledge and management of Non consensus project.

non consensus project; project establishiment; decision-making; fuzzy evaluation

2017-03-14

刘文波(1970-)，男，上海人，上海新能源科技成果转化与产业促进中心主任、书记，高级工程师，在职在读博士，研究方向：科技管理。Email:wbliu@snec.sh.cn

1005-9679(2017)04-0064-05

G 304

A