基于Matlab PDETOOL的渗流力学可视化教学与上机实验

苏关东， 顾 勋， 赵兰苓， 孙德永， 韩贝宇， 陈林辉

(1.中国石油大学(北京) a.石油工程学院； b.理学院,北京 102249；2.新疆医科大学 基础医学院,乌鲁木齐 830011)

基于Matlab PDETOOL的渗流力学可视化教学与上机实验

苏关东1a， 顾 勋1a， 赵兰苓1b， 孙德永1a， 韩贝宇1a， 陈林辉2

(1.中国石油大学(北京) a.石油工程学院； b.理学院,北京 102249；2.新疆医科大学 基础医学院,乌鲁木齐 830011)

为提高渗流力学的课堂效率，针对渗流力学学科自身的特点及其在教学实践中普遍存在的问题，提出了将MatlabPDE工具箱引入课堂的教学方法：介绍了利用Matlab中的PDE工具箱(PDETOOL)对渗流力学中经典数学模型进行求解的方法和步骤，归纳了常见的油气渗流数学模型和边界条件，并利用PDETOOL对渗流力学中一源一汇、两源两汇、稳定渗流、弹性不稳定渗流等经典的模型进行了数值模拟，实现了各经典渗流模型压力场、流场的可视化，有利于帮助学生理解流函数、压力波、导压系数等抽象概念，加深学生对压力波传播，不稳定渗流压力衰竭等抽象过程的感性认识，提升学生上课的兴趣和热情；同时提出了在渗流力学教学过程中增设上机实验内容的教学建议，充分发挥可视化教学的优势，为数值模拟、油藏工程等课程打基础，使学生对石油工程整个专业的知识体系产生宏观的认识，提高教学质量。

PDE工具箱； 渗流力学； 偏微分方程； 数值模拟； 可视化； 教学

0 引 言

渗流力学(fluid flow in porous media)是研究流体在多孔介质中运动规律的学科，是流体力学的一个重要分支[1], 主要研究油气水等在岩石这种多孔介质中的流动规律以及血液在毛细血管及微毛细血管网络中的流动规律。石油工程专业，渗流力学课程属于专业主干课和专业基础课，这门课程主要研究地下油、气、水及其混合物在地层中的流动规律[1-2]，它在石油工程专业课程体系中处于承上启下的重要地位，类似于材料力学在土木工程专业知识体系中的地位，它以高等数学、油层物理等课程为基础，同时又为油藏工程、采油工程、数值模拟等课程提供理论基础和依据。

渗流力学对石油工程专业知识体系而言，其重要性毋庸置疑，但是它的教学难度也不可忽视：从研究对象来看，由于渗流力学所研究的油气水赋存于地下，其运动状态无法观察，使得学生缺乏对渗流的形象认识；从研究手段来看，渗流力学主要以欧拉方法(场论)来描述地下油气水的运动，以微分方程为数学工具对地下油气水的流动进行研究，因为微分方程理论本身就具有一定的学习难度，使得渗流力学的学习难上加难，以至于渗流力学课程具有理论性强、逻辑性严密、公式多等特点，在教学实践中出现了教师教学难、学生学习效果差等教学现状[3]。

PDETOOL是Matlab中一个基于有限元方法求解偏微分方程的工具箱，由于其具有操作简便，可视化效果好，而被广泛用于热传导[4-5]、油气管道集输[6]、煤层气扩散[7]、电磁场[8]、应力场[8-11]、地下水渗流[12]等领域的数值模拟。本文将其运用到渗流力学的教学中，不仅可有针对性地从教学方法和教学手段上解决目前渗流力学教学实践中普遍存在的问题，同时还可以开阔学生在本专业的知识面，培养研究型人才。

在教学形式上， 教师不仅可以在课堂上展示可视化仿真结果，还可以根据课时安排，以上机实验或者课后大作业的形式进行仿真可视化教学，增加学生对仿真过程的体验，以期达到最好的教学效果。

1 基于PDETOOL的偏微分方程的解法

偏微分方程数学模型包括：四类偏微分方程模型和两类边界条件。这四类偏微分方程分别是椭圆型(Elliptic)、抛物型(Parabolic)、双曲型(Hyperbolic)，本征值方程(Eigenmodes)，其中双曲型偏微分方程和抛物型偏微分方程涉及到时间变量，可用于动态的数值模拟；两类边界条件包括：狄里克雷边界条件(Dirichlet)和诺曼边界条件(Neumann)，偏微分方程模型及其边界条件的基本形式归纳如表1所示[6,13-15]

表1 偏微分方程基本类型及边界条件

解偏微分方程的方法主要有3类[4]，包括：有限差分法、有限元法和谱方法。其中，使用有限元法时可以直接利用MATLAB中的PDE工具箱(PDETOOL)进行求解，操作简单易学，可视化效果好，运用在教学中有利于帮助学生理解各种抽象的渗流场，激发学生们的学习兴趣，提高教学质量。

2 油气渗流的数学模型

流体在多孔介质中的渗流按照流体的压力场是否随时间变化可以分为两大类：稳定渗流和非稳定渗流，分别对应不同的微分方程数学模型，它们的基本形式和在Matlab PDETOOL中的参数设置及模型的适用条件归纳如表2所示[16-17]。表2中p,K,μ,Ct,t分别为压力、渗透率、黏度、综合弹性系数和时间。对于具体的问题还需要知道边界条件和初始条件才可以得到偏微分方程的解。

油藏的边界条件分为两类：外边界条件和内边界条件，外边界条件指的是处于油藏外部，一般由地质作用形成的边界所满足的水力学条件，由油藏的成藏过程决定，主要分为供给边界和封闭边界；而内边界条件指的是在油藏内部、一般由人工钻井而形成的边界所满足的水动力学条件，由生产制度决定，可分为定压边界条件和定产边界条件。外边界的数学表达形式以及其对应的地质条件和内边界的数学表达形式及其对应的生产制度如表3所示。表3中pe,pw,A,Q分别为供给压力，井底流压，渗流截面积和产量。

表2 渗流力学的数学模型

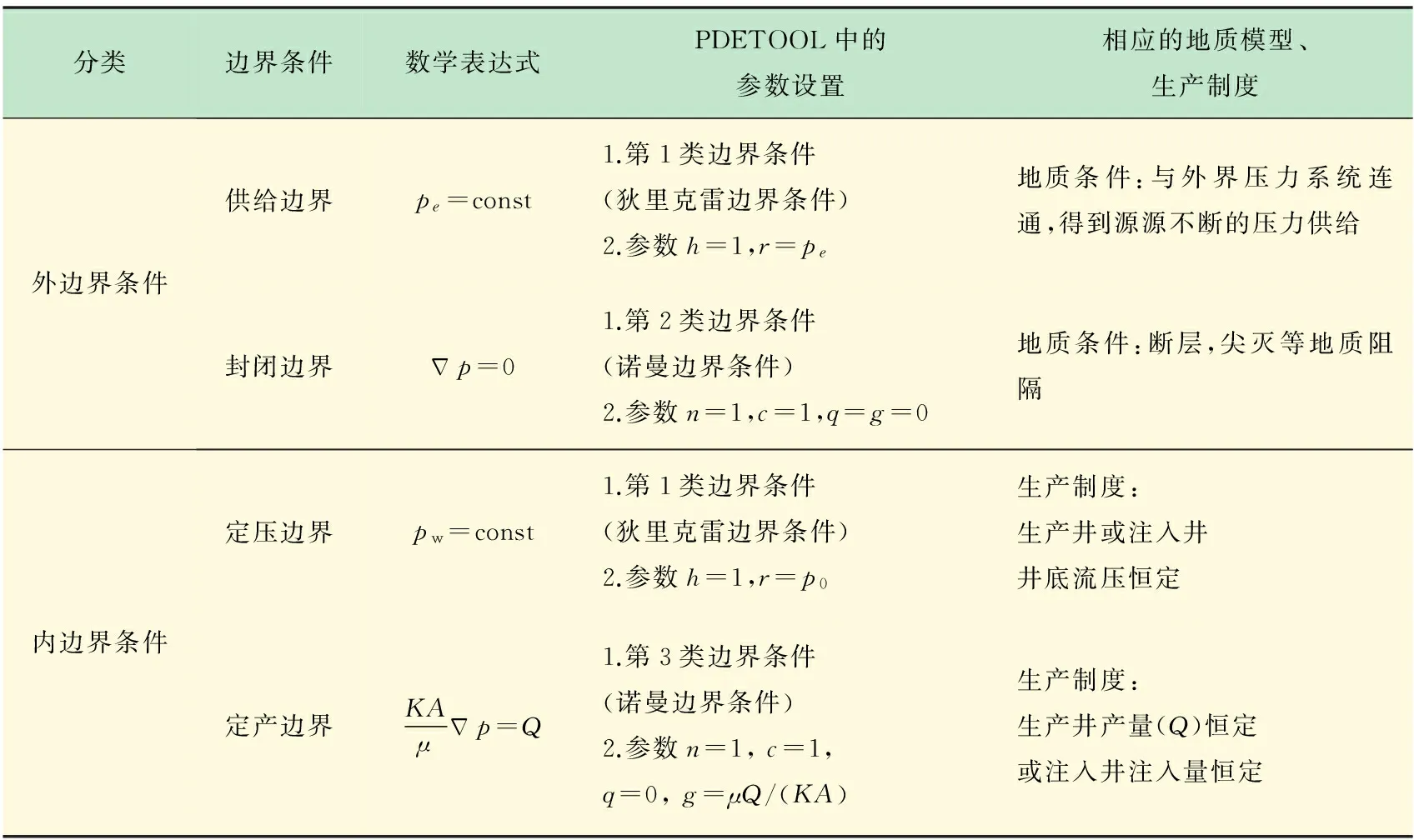
表3 渗流力学数学模型的边界条件

根据渗流力学的基本模型，结合Matlab PDE工具箱的功能特性，并借鉴文献[6-12]所用的相关方法，设计流程框图，得到利用PDE工具箱解渗流数学模型的流程图，如图1所示。

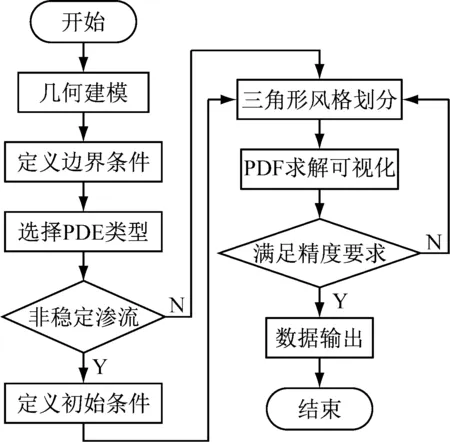
图1 PED工具箱解渗流数学模型流程图

3 算 例

算例部分通过3个典型的案例，进一步介绍使用PDETOOL求解二位渗流场的方法，同时为教师课堂教学实践提供教案参考。这3个经典案例分别是：一源一汇、两汇、水平井开发油藏渗流模型，无解析解的渗流模型，五点井网法开发油藏动态模型。

3.1 经典稳定渗流场数值模拟

算例1 如图3所示，一均质地层供给边界为半径1 000 m的圆(可近似看作无限大地层)，在距离圆心400 m处，以圆的直径为对称轴，打两口井，分别求出两口井都是生产井(两汇)时，以及一注一采(一源一汇)时的压力分布。用水平井段为1 000 m的水平井生产压力分布又如何？

解 用一源一汇、两汇、水平井3种方式生产油藏的压力分布图分别如图2～4所示。

由图2(b)可见：在注水井和生产井处分别产生一个高压峰和低压谷，对应图2中流线由注水井指向生产井；图2(a)中，在近井地带，等压线较密，压力梯度大，与图2(b)对应，可见近井地带的压力漏斗，根据达西定律可推断两井中心的连线流量最大，为主流线所在的位置，对应图2(b)中明显可见：两井连线的中轴线上的压力分布与外边界的供给压力一致，因而可等效为供给边界；在油藏的外围等压线较疏，压力梯度较小，对应图2(b)中的压力坡降平缓，甚至几乎没有明显变化。

(a)

(b)

由图3(b)可知，与以一源一汇的方式相比，当以两汇的方式生产时，同样可见压力漏斗，不同的是出现了两个低压谷，同时在两井连线的中轴线上，出现了一个极值点(高压中心)，此时在该点附近的流体由于压力相对较低，势能相对较小而无法跨越该点，从一口生产井流向另一口生产井，因而使该中轴线成为分流线，等效于断层，对应图3(a)中的中轴线附近的流线只沿着中轴线流动而无法穿越中轴线，而处于该点的流体也因此无法被采出而形成死油点。

同时，通过图2、图3的对比可以看出：在一源一汇、一注一采情况下，压力场是以两井连线的中垂线为中心对称轴，中心对称分布的；而在两汇的情况下，压力场是以两井连线的中垂线为对称轴，轴对称分布的。这也是在渗流力学中，用镜像原理来求解渗流数学模型的事实依据。

由图4与图3对比可知，采用水平井生产时，井壁与油藏的接触面积增大，蓝色部分的低压中心区域面积明显扩大，即泄油面积扩大，从而增大了单井产量；同时，低压区的扩大也可以解释当水平井作为注入井时，相对于直井具有较低的注入压力的原因。

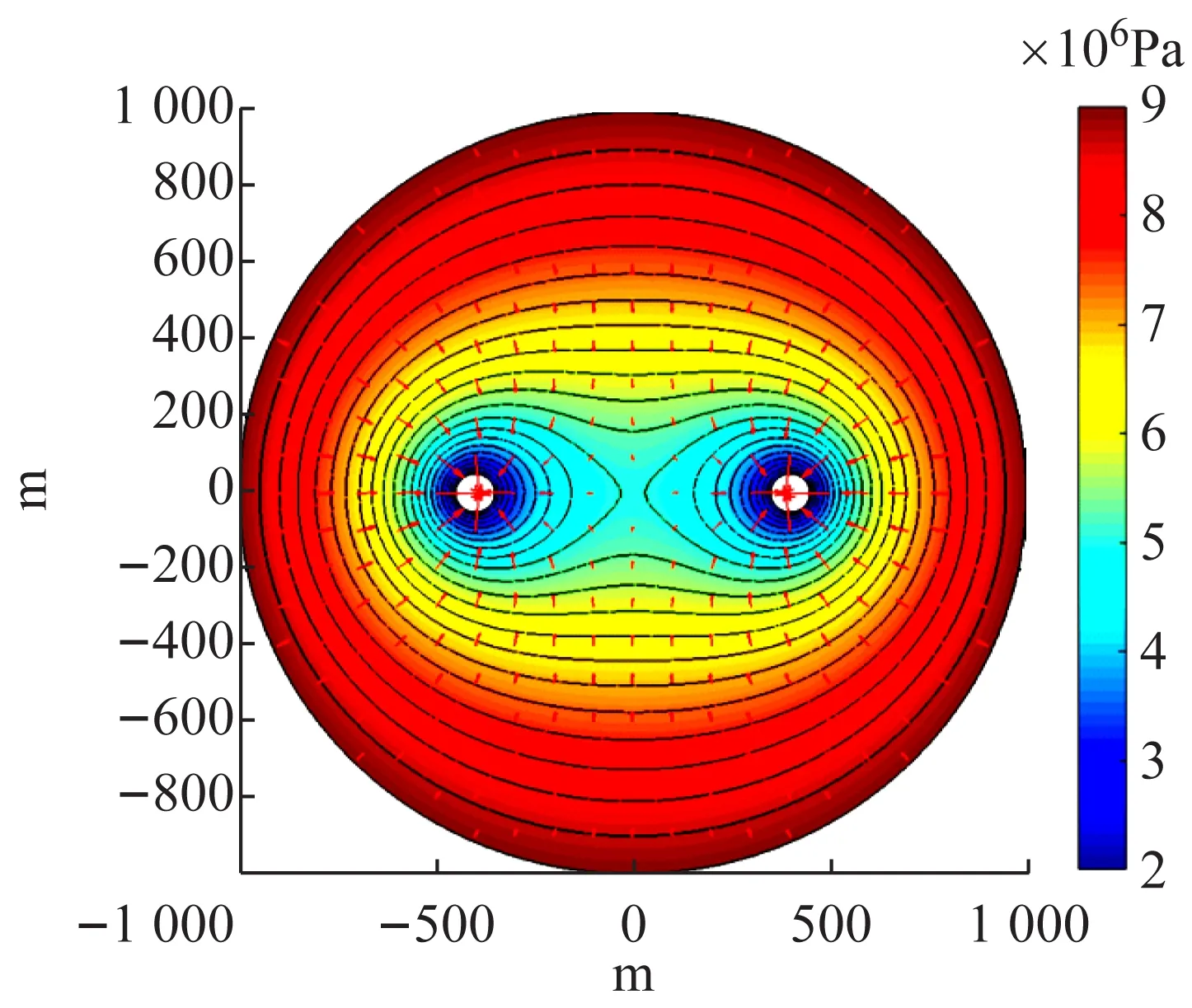
(a)

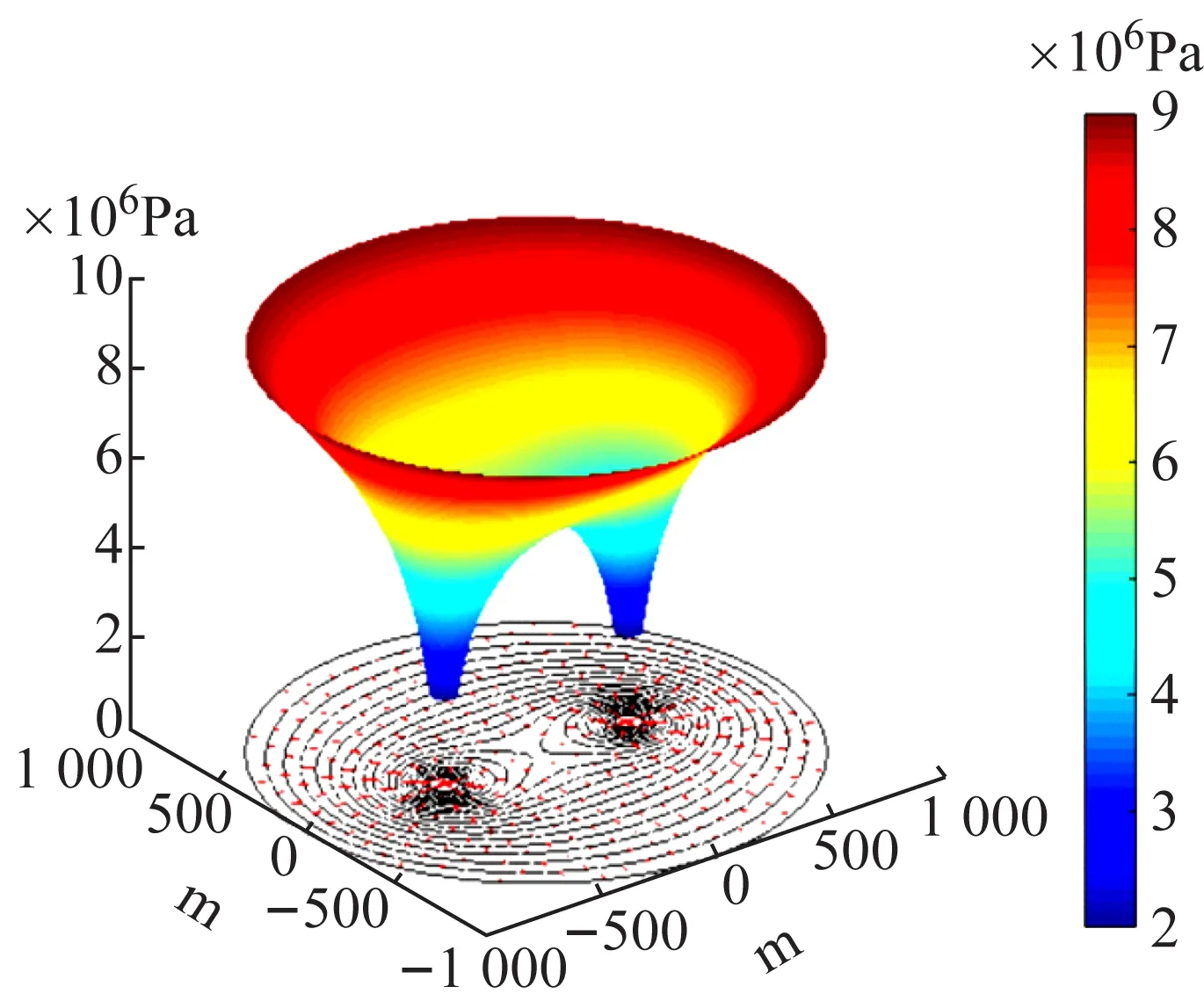
(b)

(a)

(b)

3.2 无解析解的稳定渗流场数值模拟

算例2 如图5(a)所示，在一个水平无限大的均质等厚地层中， 直线断层边界和直线供给边界夹角约为60°，对称于两个边界位置上有一口生产井，生产井距离直线断层的距离约为200 m，泄油区供给半径re为5 km，井半径rw为0.1 m，供给边界上压力pe为20.0 MPa，井底流压pw为4.0 MPa，地层渗透率K=0.8 μm2,地层厚度h=10 m，液体黏度μ=4 mPa·s，求地层压力场及流场分布。

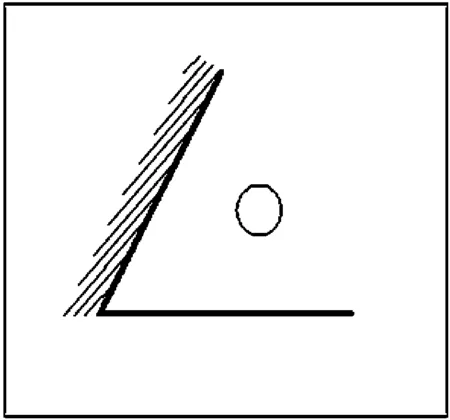
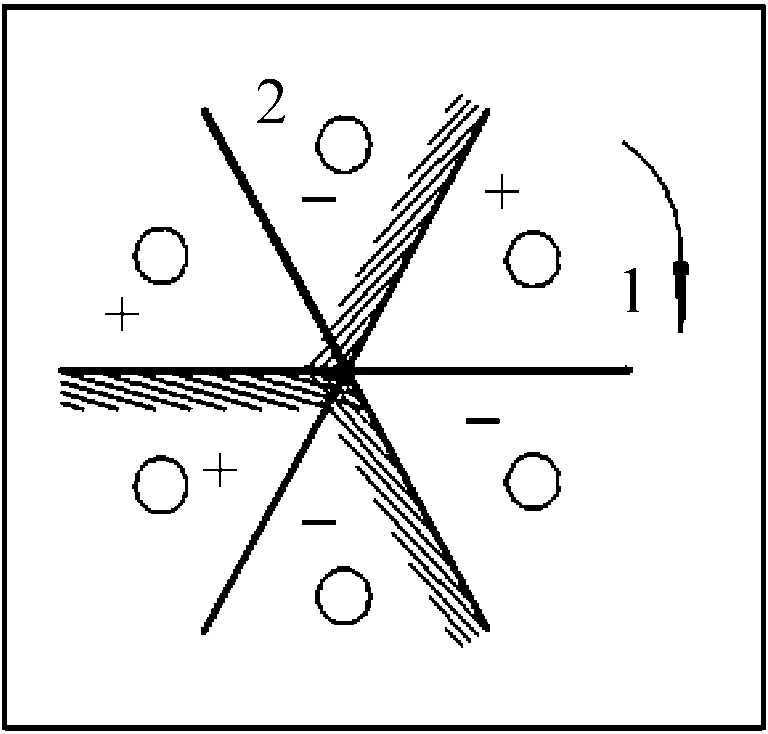
(a) (b)

图5 油藏地质模型及其镜像原理解法示意图

解法1(镜像原理)

根据镜像原理：以封闭边界(断层)为对称轴作的井为同号井，以供给边界为对称轴作的井为异号井(正号井为生产井，负号井为注水井)，按顺时针方向依次做镜像井，结果如图5(b)所示，1号井(生产井)按顺时针镜像得到的2号井为注水井，而按照顺时针镜像得到的2号井应该为生产井，自相矛盾，说明镜像原理——用于求解压力分布解析解的方法在这种情况下不适用，即该微分方程在此边界条件下没有解析解。

通过本例，教师即可以让学生认识到解析方法在实际生产应用中的不足，同时还可以顺势简单地介绍一下油藏数值模拟这门课程的基本任务和基本方法以及常用的油藏数值模拟软件例如：Eclipse，CMG等，既提高了学生的学习兴趣，又能使课堂的内容更贴近生产实际，还可以使学生在学习油藏数值模拟这门课程时更加容易接受；在教学安排上，教师既可以将本例在课堂上用解法2演示一遍，也可以提供基本的思路将本题布置成作业，供学生课后探究。

解法2(用Matlab的PDETOOL进行求解)

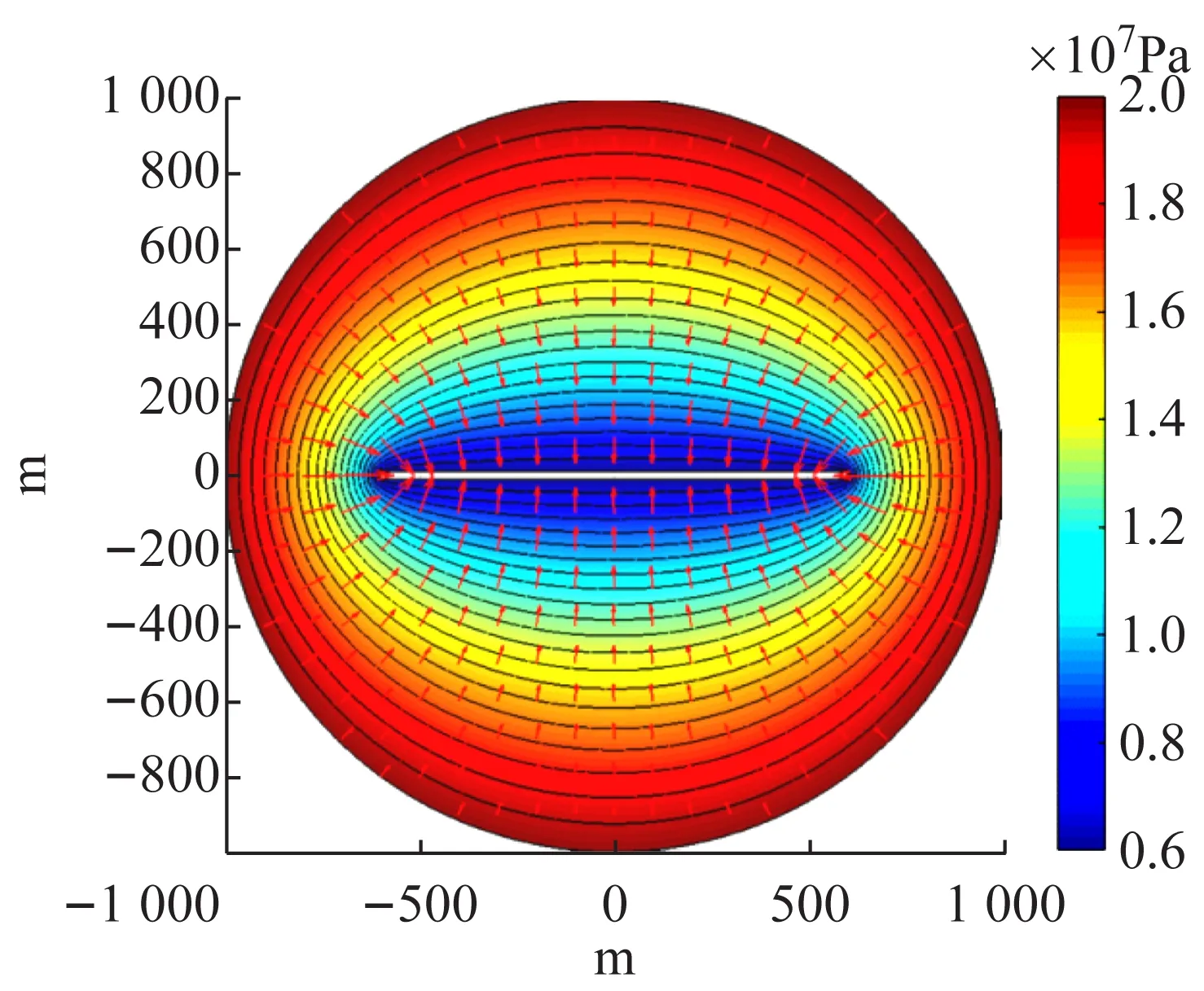
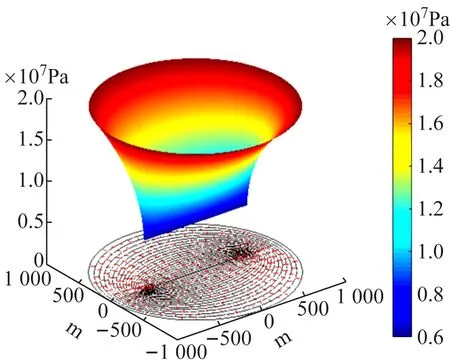
按照题中给出的已知条件设置PDE参数，并将得到的数值解可视化如图6所示。由图6(a)可见，供给边界与流线垂直，与等压线和等势线相切(平行)，说明供给边界为流体提供地下渗流的能量，“推”着流体向井口运动；而封闭边界则与流线相切(平行)，与等势线等压线垂直，说明流体只能够贴着封闭边界运动而不能穿过封闭边界；同时，封闭边界垂直截断等势线也说明了压力波无法穿透封闭边界，这也是流体无法穿过封闭边界的动力学原因。

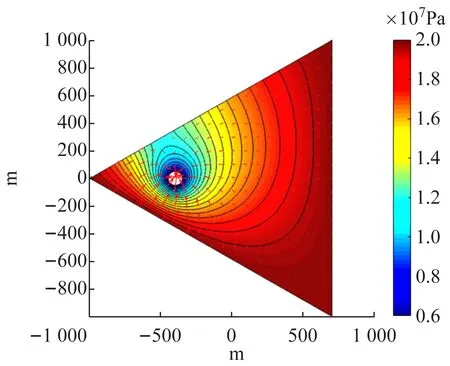
(a)

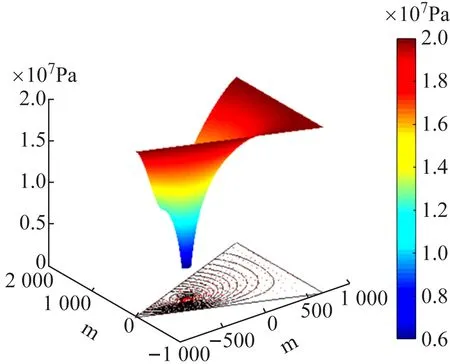
(b)

近井地带的等压线比较紧密，远井地带的等压线比较稀疏，说明在生产井附近，压力下降较快，生产井对近井地带的压力场影响较大，对应图6(b)中可见压力漏斗。

3.3 不稳定渗流场数值模拟

算例3(五点井网法) 如图7(a)所示，有一足够大水平均质油藏(可视为无限的地层)，以五点井网法对其进行开发，注水井压力pe=10.0 MPa，生产井井底流压为pw=7.5 MPa，油井半径rw=0.1 m，地层厚度h=5 m，渗透率K=1 μm2，黏度μ=4 mPa·s，注水开发周期为T，求该过程中地层压力场和速度场分布？

解 为了对油藏渗流模型进行求解，从井网中选取一个小单元[18]，如图7(b)所示。

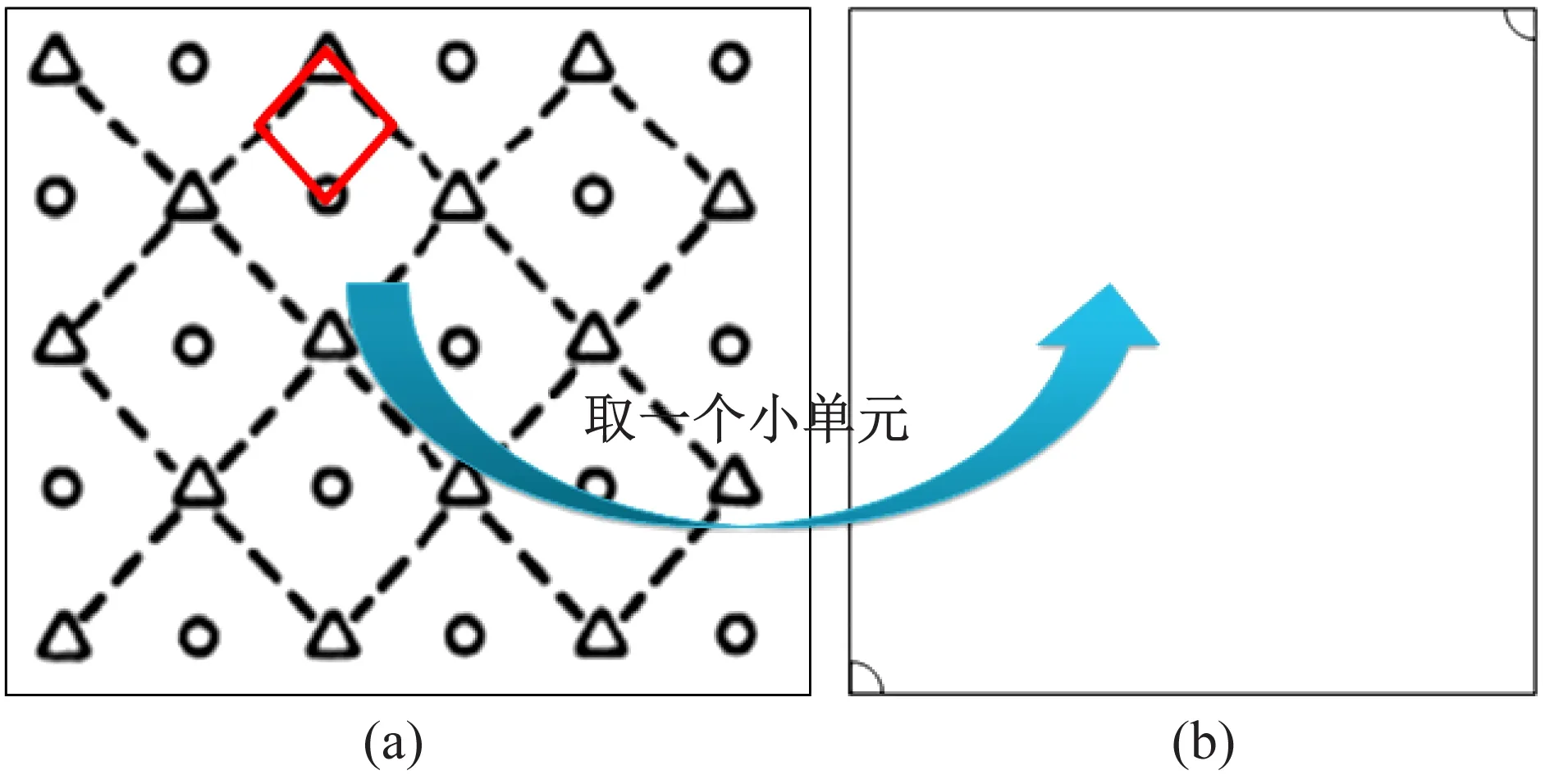
图7 五点井网及其单元示意图

由图8可知，随着时间的推移，,注水井处的压力波缓慢向采油井方向传递，高压中心扩散；采油井附近，随着地下油的采出对油藏泄压，低压中心向四周扩散。随着时间增长，压力波推进的速度越来越慢，最后几乎静止，达到准静态(拟稳态)。在最终驱替完毕时，在两井中轴线中心的区域压力值不变，这就是赋存剩余油的死油区(见图8(c))，此时应当调整注采关系(注采井网)以提高波及效率，从而提高采收率。

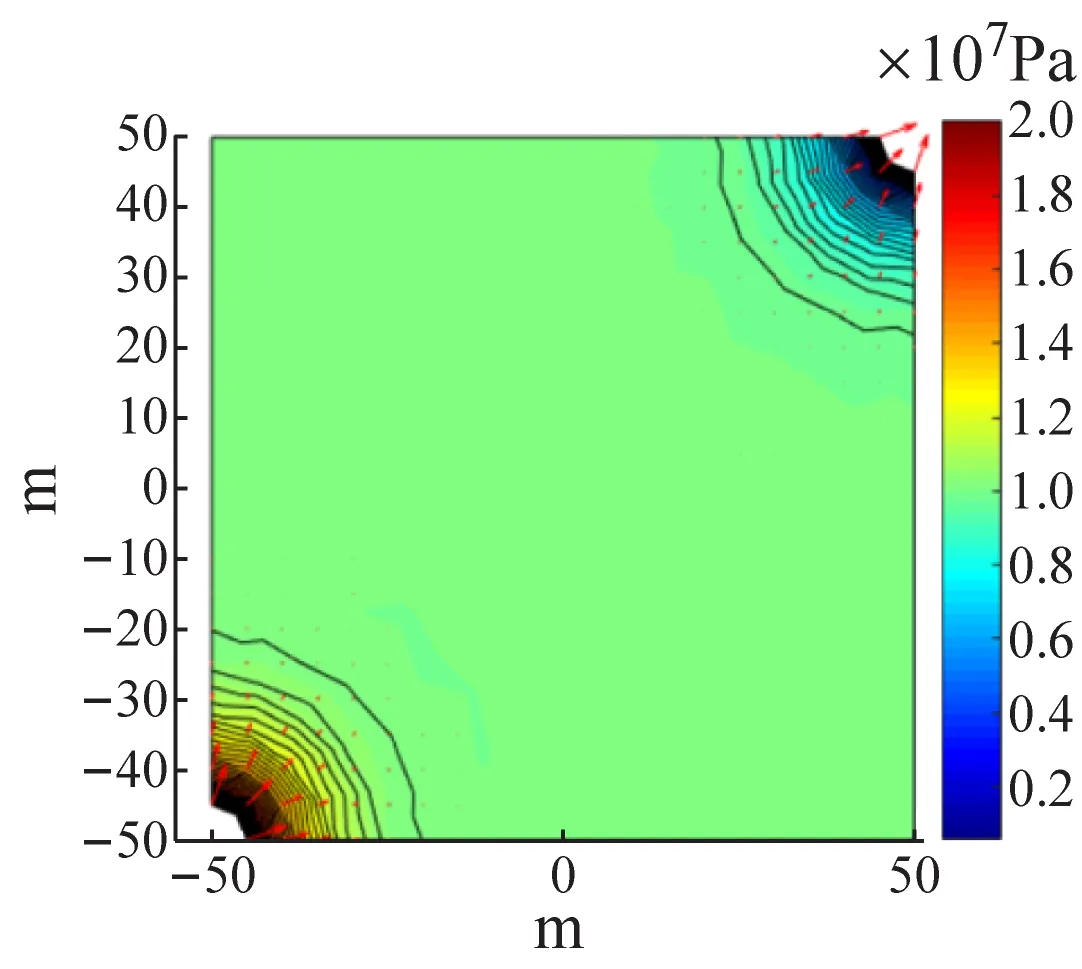
(c) t=T

图8 五点井网单元开发动态图

本例很好地展示了油藏开发从非稳态阶段到拟稳态阶段的过程，同时又和油藏工程数值模拟紧密联系，有利于学生理解油气田开发的动态过程。

特别说明：由于PDETOOL本身的不完善性，在教学实践中大可不必严格拘泥于物理模型和数值模型的几何比例关系，可以为了达到较好的可视化效果而对其进行适当调整。

4 结论与展望

(1) 归纳总结了用Matlab自带的PDE工具箱对偏微分方程的求解方法和基本流程以及常见的油气渗流数学模型及边界条件。

(2) 用PDETOOL对渗流力学中经典的一源一汇，两汇，水平井等渗流模型以及五点井网法开发油藏的动态过程进行了数值模拟，有利于加深学生对渗流力学理论的理解，同时为教师课堂教学实践提供教案参考。

(3) 提出了相关的教学建议：除了在课堂上演示渗流场的可视化过程外，还可以在渗流力学教学实践中，根据具体情况，增设上机实验的内容，既可以上机实验课的形式进行， 也可以课后报告的形式进行，丰富课堂形式，使学生投入到可视化教学的体验中，以充分发挥可视化教学的优势。

(4) 将PDE工具箱引入渗流力学的教学，不仅有利于学生对抽象的渗流理论产生形象化的认识，提高教学质量；同时有利于学生提前了解油藏工程、数值模拟等课程，对石油工程专业知识体系有全面的认识，提高毕业生的质量。

致谢 感谢中国石油大学(北京)石油工程学院渗流力学本科教研组的支持与帮助。衷心感谢中国石油大学(北京)理学院赵兰苓老师的指导以及在论文修改上的帮助。特别感谢中国石油大学(北京)石油工程学院庞占喜老师、涂斌老师和李春兰老师给予的帮助。特别感谢中国石油大学(北京)石油工程学院隋微波老师、朱舟元老师和东晓虎老师提供的部分图片。衷心感谢中国石油大学(北京)郑力会教授、张鹏教授给予的鼓励。

[1] 宋洪庆，姜琳婧，朱维耀，等. 渗流力学课程研究型教学探索[J]. 中国冶金教育, 2014(2): 5-7.

[2] 袁迎中，戚志林，严文德，等. “渗流力学”课程创新思维教学方法探索[J]. 中国地质教育, 2014(2): 60-62.

[3] 陈军斌. “油气渗流力学”课程教学改革的研究与实践[J]. 石油教育, 2016(3): 32-35.

[4] 张哲任，徐 政，徐 韬，等. 采用有限体积法的特高压直流输电系统接地极稳态温度场仿真分析[J]. 高电压技术, 2012，38(2): 328-334.

[5] 叶长燊. MATLAB在稳态与动态导热过程分析中的应用[J]. 计算机与应用化学,2006, 23(10): 986-990.

[6] 张纯静，申龙涉，杜义朋，等. MATLAB PDE工具箱在稠油输送管道中的应用[J]. 当代化工, 2012, 41(1): 48-49.

[7] 马 胜，虞青松. MATLAB在模拟煤层气扩散中的应用[J]. 山西焦煤科技, 2012(1): 44-45.

[8] 黄作英，阙沛文. 基于MATLAB的电磁场数值分析[J]. 计算机工程与应用, 2004(36): 196-198.

[9] 李 彤，刘阿龙. 基于MATLAB的圆环承受均布压力分析[J]. 机械工程与自动化,2008(2): 14-16.

[10] 潘东辉，马崇武. MATLAB/PDE在弹性力学可视化教学中的应用[J]. 力学与实践, 2014, 36(4): 500-504.

[11] 徐 勇，李顺才，佟军民. 基于MATLAB的平面应力问题研究[J]. 煤矿机械, 2003(10): 60-62.

[12] 牛 宏，梁 杏，尼胜楠，等. MATLAB PDE工具箱在地下水科学实验教学中的应用[J]. 安全与环境工程, 2013, 20(6): 6-11.

[13] 冯桂莲. 偏微分方程的MATLAB数值解法及可视化[J]. 计算机技术与发展, 2013, 23(12): 120-123.

[14] 李 明. 偏微分方程的MATLAB解法[J]. 湖南农机, 2010, 37(5): 89-91.

[15] 田 兵. 用MATLAB解偏微分方程[J]. 阴山学刊(自然科学版), 2006, 20(4): 12-13.

[16] 刘慧卿.油气渗流力学基础[M]. 北京:中国石油大学出版社, 2013:30-47.

[17] 程林松.渗流力学[M]. 北京:石油工业出版社, 2011:1-23.

[18] 董平川，韩德金，牛彦良，等. 油藏多相渗流的面向对象有限元程序设计[J]. 岩土力学, 2009, 30(4): 1115-1121.

Visual Teaching and Computer-based Experiment of Fluid Flow in Porous Media with PDETOOL of Matlab

SU Guandong1a， GU Xun1a， ZHAO Lanling1b， SUN Deyong1a， HAN Beiyu1a， CHEN Linhui2

(1a. College of Petroleum Engineering, 1b. College of Science, China University of Petroleum (Beijing), Beijing 102249 China; 2. School of Basic Medical Sciences，Xinjiang Medical University, Urumqi 830011 China)

In order to improve the classroom efficiency and the teaching quality of the course of fluid flow in porous media, the teaching method of introducing Matlab PDETOOL into the classroom is put forward, and the method and steps to solve the classical mathematical model in fluid flow in porous media with the PDE toolbox in Matlab are introduced, according to the characteristics of the subject of fluid flow in porous media and the problems in teaching practice. The PDETOOL is used to simulate the classical models of fluid flow in porous media such as source-sink, source-sink, steady-flow, and elastic-unsteady flow in porous media. It helps students understand the abstract concepts of stream function, pressure wave and conductivity coefficient, enhances students’ perceptual knowledge of the process of the propagation of pressure wave and unsteady flow in porous media. At the same time, it is suggested to add computer-based experiment to the teaching process of fluid flow in porous media. On conclusion, this study will lay a foundation for the course of numerical simulation and reservoir engineering, so that the students will have a macroscopic understanding of the whole knowledge system of petroleum engineering.

PDETOOL; fluid flow in porous media; partial differential equations; numerical simulation; visualization; teaching

2016-11-22

国家级大学生创新创业训练计划支持项目(201611414019);中国石油大学基础研究基金(2462015YQ0604)

苏关东(1995-)，男，广东湛江人，本科生。

Tel.：18801322091;E-mail：su_gd@qq.com

赵兰苓(1977-)，女，山东泰安人，博士，讲师，研究方向：计算数学、复杂流体建模与计算。

Tel.：010-89731993；E-mail：zllblue@163.com

TE 312; O 242.1

A

1006-7167(2017)08-0137-06