基于主成分分析-协整理论的土石坝安全监控模型研究

周炜翔,张慧莉,陈 航,钟佩文

(西北农林科技大学水利与建筑工程学院,陕西杨凌712100)

基于主成分分析-协整理论的土石坝安全监控模型研究

周炜翔,张慧莉,陈 航,钟佩文

(西北农林科技大学水利与建筑工程学院,陕西杨凌712100)

结合某土石坝垂直位移监测资料,针对非平稳时间序列分析时可能产生的“伪回归”问题,采用主成分分析方法和协整理论建立土石坝安全监控模型,并对监测点的变形性态进行分析。结果表明,所建立的模型系数显著,意义明确,克服了自变量间的多重共线性以及非平稳时间序列分析时的“伪回归”问题,在监测时段内,监测点垂直位移时效基本稳定。

伪回归；主成分分析；协整理论；多重共线性；非平稳时间序列

0 引 言

在大坝安全监控领域中,统计模型是监测资料分析的基本手段之一,占有着至关重要的地位。统计模型建立的方法是:首先根据坝工知识及力学知识,得出含有参数的位移计算模型表达式,然后根据实测资料来拟合,从而得出参数值并最终确定统计模型的数学式[1]。这类统计模型主要有多元回归分析模型、逐步回归分析模型、主成分回归分析模型、时间序列分析模型等[2]。现有研究表明,混凝土坝监控模型自变量因子间普遍存在多重共线性问题,采用普通最小二乘法很难精确地分离水压、温度、时效等分量,无法对监测效应量的变化做出准确的定量分析与合理的物理成因解释。主成分分析是在保证数据信息丢失最少的原则下,对高维变量空间进行降维处理。许多研究者[3- 6]将主成分分析应用于大坝安全监测资料的分析中,以减弱自变量间的共线性对模型分析和解释能力的影响。在进行时间序列分析时,传统上要求所用的时间系列必须是平稳的,即没有随机趋势或确定趋势,否则会产生“伪回归”问题,进而影响分析的有效性。然而,对于蓄水期的混凝土坝或土石坝监测数据而言,其位移监测序列以及环境量监测序列通常是非平稳的,尽管可以通过差分来消除其趋势性,但是经过差分后的数据不但会损失一定的信息,同时其物理含义也发生了改变。Granger和Engle于20世纪80年代提出了协整理论[7- 8],其研究表明，两个或两个以上的非平稳时间序列的线性组合有可能是平稳的,如果这样的线性组合存在,那么这一组非平稳时间序列被称为是协整的,线性组合称为协整方程。经典回归分析所暗含的重要假设是数据序列是平稳的,与回归分析有着本质区别的协整则是通过对一组非平稳时间序列的线性组合,从而得到一个新的平稳序列的过程[9]。

鉴于此,本文尝试将主成分分析和协整理论相结合并应用到土石坝安全监控分析中,建立相应的安全监控模型,通过对某土石坝坝顶垂直位移的监控模型分析,验证所建模型的合理性,以期完善蓄水期土石坝安全监控模型理论。

1 研究方法

1.1 主成分分析

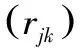
1.2 单位根检验

为避免计量分析中的伪回归现象,本文应用ADF检验(Augmented Dickey-Fuller Test)进行单位根平稳性检验。

1.3 协整分析

如果一组非平稳变量序列存在某种平稳的线性组合,即这种线性组合抵消了这组变量序列的随机趋势,那么这组变量序列就是协整的。这种平稳的线性组合称为协整方程,表示一种长期的均衡关系。本文采用Johansen协整检验进行检验,该检验是以向量自回归模型VAR模型为基础的检验方法,是一种进行多变量协整检验的方法。Johansen协整检验不仅将所有变量都作为内生变量处理,还具有较高的检验优势。

1.4 向量误差修正模型(VECM)

只要向量间存在协整关系,就可以由自回归分布滞后模型导出误差修正模型,VECM模型多应用于具有协整关系的非平稳时间序列。当系统的变量之间存在协整关系时,简单的差分VAR模型会损失掉变量间的长期信息,同时也会使分析结果出现误差,VECM模型可以较好地克服上述缺点,还能识别变量间的长期与短期的因果关系。

2 实例分析

2.1 模型选择

某土石坝坝高69.5 m,坝长218.14 m,坝顶高程2 705.0 m,水库总库容1 496.0万m3,正常蓄水位2 700.00 m。对于某蓄水期内的土石坝,现采用其坝顶监测点LD1的35组垂直位移监测数据进行分析。所采用的统计模型为

(1)

2.2 模型分析

该模型共选用5项影响因子,其中水压因子3项,时效因子2项,5个自变量的相关系数见表1。

表1 自变量间相关系数

从表1可见,自变量中的水压因子之间以及时效因子之间均存在很强的相关性。经主成分分析后,从原有的5个自变量中提取了2个新的自变量F1和F2,具体结果见表2和表3。

表2 旋转成分矩阵

根据表2和表3可以看出,F1主要解释的是水压因子,F2主要解释的是时效因子,所提取的F1和F2解释了原自变量系统中99.403%的信息,信息损失量极小。

表3 主成分分析结果

将所提取的2个主成分F1和F2以及水平位移δ采用ADF检验法进行单位根检验,检验结果见表4。

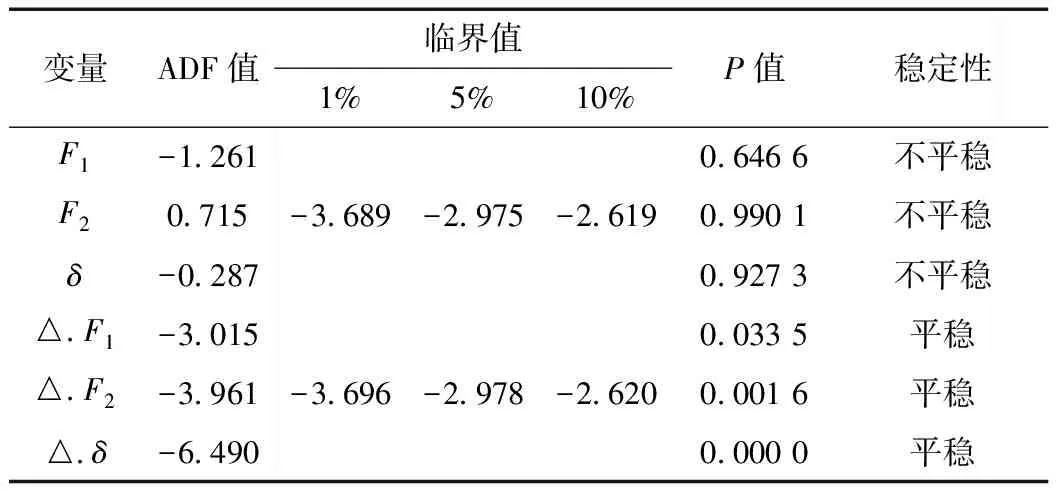
表4 变量F1、F2、δ及其一阶差分的ADF检验结果

注：△表示一阶差分；P值表示对应滞后阶数下模型的显著性。

表6 VAR滞后阶数的选取

注：FPE、AIC、HQIC、SBIC为4种信息准则，值越小，表示越应该选用。

表8 协整方程估计结果

注：表中z为协整检验中的统计量。

由表3可以看出,F1、F2以及δ均为一阶单整序列,为了验证三者之间是否存在协整关系,本文采用迹检验法对F1、F2以及δ进行协整检验。确定协整秩及滞后阶数的计算过程见表5和表6。

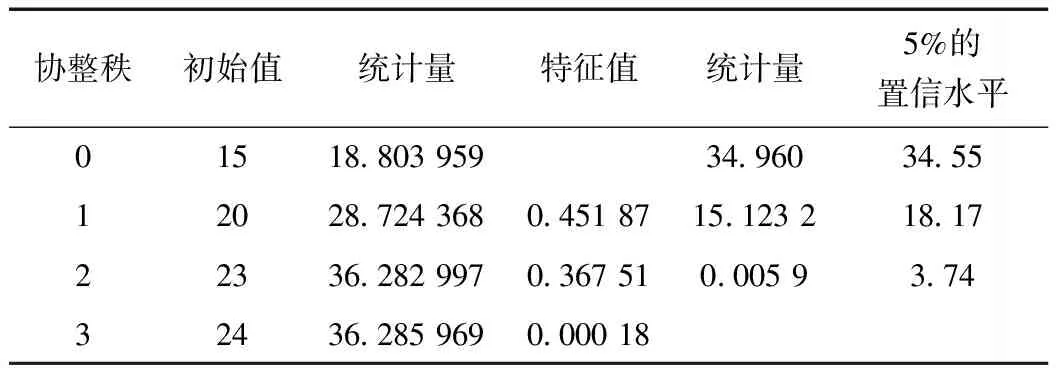
表5 协整秩的确定

根据表5和表6可以看出,协整秩为1,即只有一个线性无关的协整向量；绝大多数准则表明,选择滞后阶数为2较为合理。VECM模型和协整方程的估计结果见表7和表8。

表7 VECM模型参数估计结果

由表7、8可见,VECM模型和协整方程整体上是非常显著的,在所研究的区间内,F1、F2以及δ之间存在长期的均衡关系。方程(2)中的自变量为提取的主成分,根据得分系数矩阵即可还原为原自变量的方程

δ=-0.017H-0.000 19H2-0.000 002 6H3+

0.458θ+1.850lnθ+0.547

(2)

公式(2)表明,水压因子和时效因子对坝体垂直位移的影响较大,由于时效分量所占的比例直接关系到坝体结构的安全,因此有必要对坝体结构的稳定性进行分析。为此，可根据所建立的VECM系统是否稳定来评价坝体结构的安全与否,检验结果见图1。

图1 VECM系统稳定性判别

由图1可以看出,除了VECM系统自身所假设的单位根之外,伴随矩阵的所有特征值均落在单位圆之内,故该系统是稳定的,即表明在监测时段内,监测点垂直位移时效基本稳定,变形性态正常。

3 结 论

本文结合某土石坝垂直位移监测资料,采用主成分分析方法和协整理论建立土石坝安全监控模型,并对监测点的变形性态进行分析,得出以下结论：

(1)经过主成分分析,所提取的F1和F2解释了原自变量系统中99.403%的信息。

(2)F1、F2以及δ均为一阶单整序列,协整秩为1,滞后阶数为2。

(3)VECM模型和协整方程整体上是非常显著的,在所研究的区间内,F1、F2以及δ之间存在长期的均衡关系。

(4)在监测时段内,VECM系统稳定,监测点垂直位移时效基本稳定。

[1]吴中如. 水工建筑物安全监控理论及其应用[M]. 北京: 高等教育出版社, 2003．

[2]吴中如. 大坝的安全监控理论和试验技术[M]. 北京： 中国水利水电出版社, 2009．

[3]BEHROUZ A N. Multivariate Statistical Analysis of Monitoring Data for Concrete Dams[D]. Canada Montreal: McGill University, 2002．

[4]李雪红, 徐洪钟, 顾冲时, 等. 主成分神经网络模型在大坝观测资料分析中的应用[J]. 大坝观测与土工测试, 2001, 25(5): 14- 16．

[5]李红祥, 岳东杰, 李立瑞. 基于主成分回归的大坝位移模型[J]. 水电自动化与大坝监测, 2008, 32(5): 61- 64．

[6]虞鸿, 吴中如, 包腾飞, 等. 基于主成分的大坝观测数据多效应量统计分析研究[J]. 中国科学: 技术科学, 2010(7): 830- 839．

[7]GRANGER C W J. Some properties of time series data and their use in econometric model specification[J]. Journal of Econometrics, 1981, 16(1): 121- 130．

[8]ENGLE R E, GRANGER C W J. Co-integration and Equilibrium Correction Representation, Estimation and Testing[J]. Econometrica, 1987, 55(2): 251- 276．

[9]李国璋, 江金荣, 陈敏. 协整理论与误差修正模型在实证应用中几个问题的研究[J]. 统计与信息论坛, 2010, 25(4): 21- 24．

[10]吴中如. 水工建筑物安全监控理论及其应用[M]. 北京: 高等教育出版社, 2003．

[11]吴中如, 刘观标. 混凝土几坝的位移确定性模型研究[J]. 大坝观测与土工测试, 1987(1): 16- 25．

[12]许后磊, 冯茂静, 杨阳, 等. 因子相关性对大坝监测模型精度的形响探究[J]. 水电能源科学, 2009, 27(5): 77- 80．

[13]徐培亮. 应用时间序列方法作大坝变形预报[J]. 武汉测绘科技大学学报, 1988(3): 23- 31．

[14]张利, 李富强. 观测分析中的回归一时序列模型[J]. 浙江大学学报： 工学版, 2002, 36(5): 572- 576．

[15]郑箫, 金青. 回归模型与时问序列在大坝变形监测中的应用[J]. 湖北师范学院学报: 自然科学版, 2010, 30(1): 83- 88．

(责任编辑 焦雪梅)

Research of Safety Monitoring Model Based on Principal Component Analysis and Cointegration Theory

ZHOU Weixiang, ZHANG Huili, CHEN Hang, ZHONG Peiwen
(College of Water Resources and Architectural Engineering, Northwest A&F University, Yangling 712100, Shaanxi, China)

Aiming at the problem of spurious regression when analyzing the non stationary time series, the safety monitoring model of earth-rockfill dam is established based on principal component analysis and cointegration theory to analyze the deformation behavior of monitoring stations combined with the vertical displacements monitoring data of an earth-rockfill dam. The result shows that the model has significant coefficient and definite meaning, and meanwhile, it can overcome the multi-collinearity of independent variables and the problem of spurious regression in analyzing the non stationary time series. The vertical displacements of monitoring stations are stable during monitoring period．

spurious regression; principal component analysis; cointegration theory; multicollinearity; non stationary time series

2016- 07- 06

周炜翔(1992—),男,山东临沂人,硕士研究生,研究方向为大坝安全监测．

TV641.1;TV698.1

A

0559- 9342(2017)05- 0108- 04