地震激励下管-土动力相互作用试验研究

曹文冉，商宁宁，邓海峰，许 浩，毛天宇

1.中国石油集团工程技术研究院，天津 300451

2.中国石油天然气集团公司海洋工程重点实验室，天津 300451

地震激励下管-土动力相互作用试验研究

曹文冉1，2，商宁宁1，2，邓海峰1，2，许 浩1，2，毛天宇1

1.中国石油集团工程技术研究院，天津 300451

2.中国石油天然气集团公司海洋工程重点实验室，天津 300451

海底管道的建设往往要考虑地震的影响，而管-土相互作用机理则是进行埋地管道抗震分析的基础。基于Cauchy原理和Buckingham π定理进行了试验相似比设计，以保证模型与原型相似，研制了叠层剪切箱来模拟地基边界效应，探讨了管-土间相对位移的试验量测方法，考察了管道埋深、地震动峰值、远近场地震动类型等因素对埋地管道抗震性能的影响，获得了管-土接触面相对位移、管道应变分布等试验数据，分析了管道应变与土体位移的关系。试验发现：管道与土体间的相对位移是管道结构产生应变的主要原因，土体本身以及管-土接触面的非线性发展是影响管-土相互作用程度的决定因素。

振动台；管-土相互作用；接触面相对位移；管道应变；土体位移

随着海洋油气资源的不断开发，海底管道在我国得到了广泛应用[1]，发挥着越来越重要的作用。与陆地管道相比，海底管道具有造价昂贵、维修复杂、维护费高等特点[2]，加之我国是一个多地震国家[3]，蕴藏丰富油气资源的渤海、黄海、东海等海域又濒临环太平洋地震带[4]，属于地震高发区域，地质条件差别较大，给海底管道的设计、施工带来了诸多技术难题。因此，我国海底管道的建设往往要考虑地震的影响。

管-土相互作用机理是进行埋地管道抗震分析的基础。40多年来，国内外学者围绕管道抗震开展了大量研究[5-10]，并提出了一些计算方法，但这些理论方法的验证都离不开实际震害资料。由于强震的罕遇性和地震的不可控性，缺少管-土体系在其作用下的实测数据是当前最大的困难，使得已有的理论成果很难被及时检验和修正。因此，试验手段在验证理论计算模型和探索管-土相互作用机理中就起到了举足轻重的作用。

为了保证埋地管道模型试验与原型相似，本文基于Cauchy原理和Buckingham π定理进行了试验相似比设计，采用叠层剪切箱来模拟地基边界效应，探讨管-土间相对位移的试验测量方法，考察管道埋深、地震动峰值、远近场地震动类型等因素对埋地管道抗震性能的影响，以期获得管-土接触面相对位移、管道应变分布等试验数据，同时分析土体相对位移与管道应变的关系，从而为验证理论模型和计算方法的合理性打下基础。

1 模型试验准备

1.1 试验相似比设计

为了考察埋地管道的管-土动力相互作用规律，模型必须满足动力相似条件，包括物理条件、边界条件、几何条件、动平衡方程式和运动初始条件等五个方面。由于试验所模拟场地的复杂性，人工质量相似律因能同时满足重力和惯性力的相似条件而得到了广泛应用，但是振动台的承载力有限，在大型结构的缩尺模型上附加人工质量很难实现，加之线性结构的刚度在动力响应时必须满足相似条件，因此本文试验的相似比设计采用忽略重力的模型，选择几何相似比、密度相似比、动弹性模量相似比三个模型独立参数作为基准，按照Cauchy原理，采用量纲和谐性分析方法，根据Buckingham π定理，求取π因子并建立各物理量的关系，进而推导出其他单位量的相似比关系，结果见表1。

表1 模型相似关系

1.2 叠层剪切箱制作

结合振动台的几何尺寸和承载能力，本文自主设计并加工制作了可沿管道方向振动的叠层剪切箱，见图1。

图1 叠层剪切箱装置

箱体尺寸为2100mm（长）×1600mm（宽）×1570mm（高），底座尺寸为2460mm（长）×2250mm（宽）×120mm（高），采用13层钢质框架叠合而成，每层框架高100mm，由4根100mm×3mm方形钢管拼接而成，相邻两层框架之间由定向滑动装置支撑，可使框架之间产生定向水平相对位移，以满足模型地基的水平层状变形要求。

在垂直于振动方向的每个横向侧面，设计了相同尺寸（1570mm×440mm）的3块钢板，可根据试验要求选择钢板数量并以螺栓方式改变位置，既能提高钢板使用的灵活性，又能满足改变箱体刚度的要求。箱体纵向两侧分别安装2根钢质立柱，柱体上均匀布置滚动轴承，柱底与箱体底座焊接，柱顶用2根方形钢管栓接，以限制箱体的垂直运动和平面扭转运动。此外，箱体内壁衬3mm厚的特制橡胶垫，以防止土体从框架间隙漏出。

为了保证土体在振动中起控制作用，采用扫频方法测得：空箱基频为1.25Hz，满箱基频为3.66Hz，可见空箱频率远离满箱频率。另外，根据自由振动衰减法获得的箱体阻尼比为0.0213，小于土体的阻尼比0.05～0.25。因此，在本文振动台模型试验中，剪切箱不会给模型土的地震反应带来不良影响，即模型土与原型土具有相同的运动规律。

叠层剪切箱可以通过底座螺栓固定在振动台台面上，如图1所示。

1.3 试验材料及仪器

试验土体取自哈尔滨市松花江边，土体类别为中砂，密度1.56t/m3，内摩擦角29.3°。试验前对模型土体进行分层夯实，使箱内土层高度约1.5m。

试验选用的钢管规格为D 114.3mm×4mm，试验长度取2.5m，材质为API 5LX65，屈服强度为448MPa，抗拉强度为531MPa。

试验仪器见表2。

2 模型试验方案

2.1 传感器布置方案（见图2～4）

箱外沿竖向布置拉线位移计，用以监测各层土体的水平位移，进而了解各层土体的水平动态位移变化趋势；箱内沿水平向布置加速度计，用以监测各层土体在地震波输入方向的模型箱效应；沿竖向布置加速度计，用以监测各层土体振动沿竖向的变化情况；箱体底座顶面布置加速度计，用以监测输入波在振动台面上的变化。

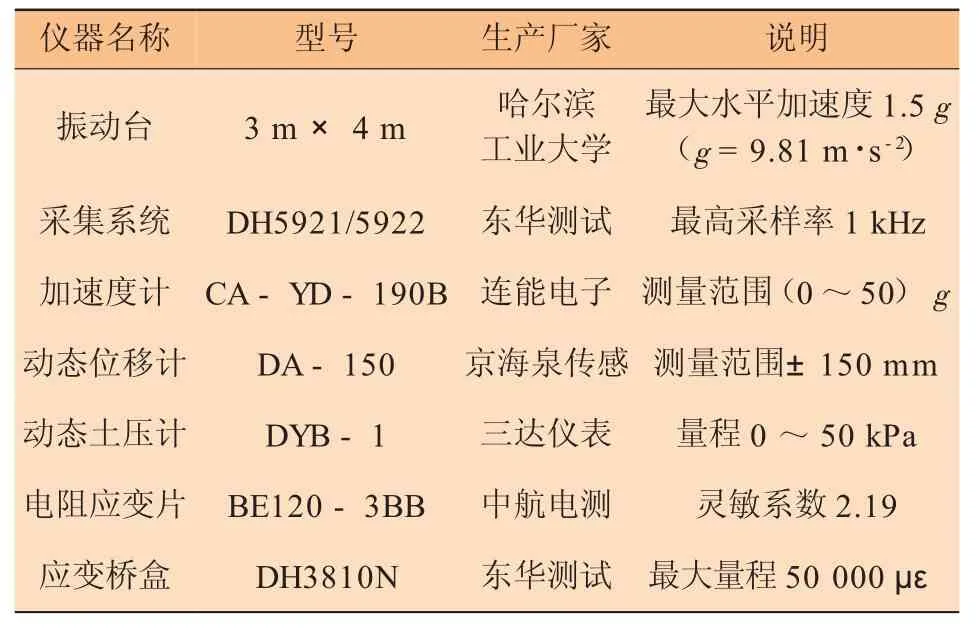
表2 试验仪器

模型管外表面布置加速度计，用以监测管道在地震波输入过程中的动力特性变化；管体左端布置拉线位移计，用以监测管-土接触面相对位移发展的不同趋势；沿管长不同位置布置动土压力计，用以监测地震波输入过程中管道周围土体的动土压变化；环绕管体外表面布置土压计，用以监测在地震波输入过程中环管的土压分布状态；沿管体轴向水平对称布置应变片，用以监测振动过程中钢管应变的分布情况及其发展变化。

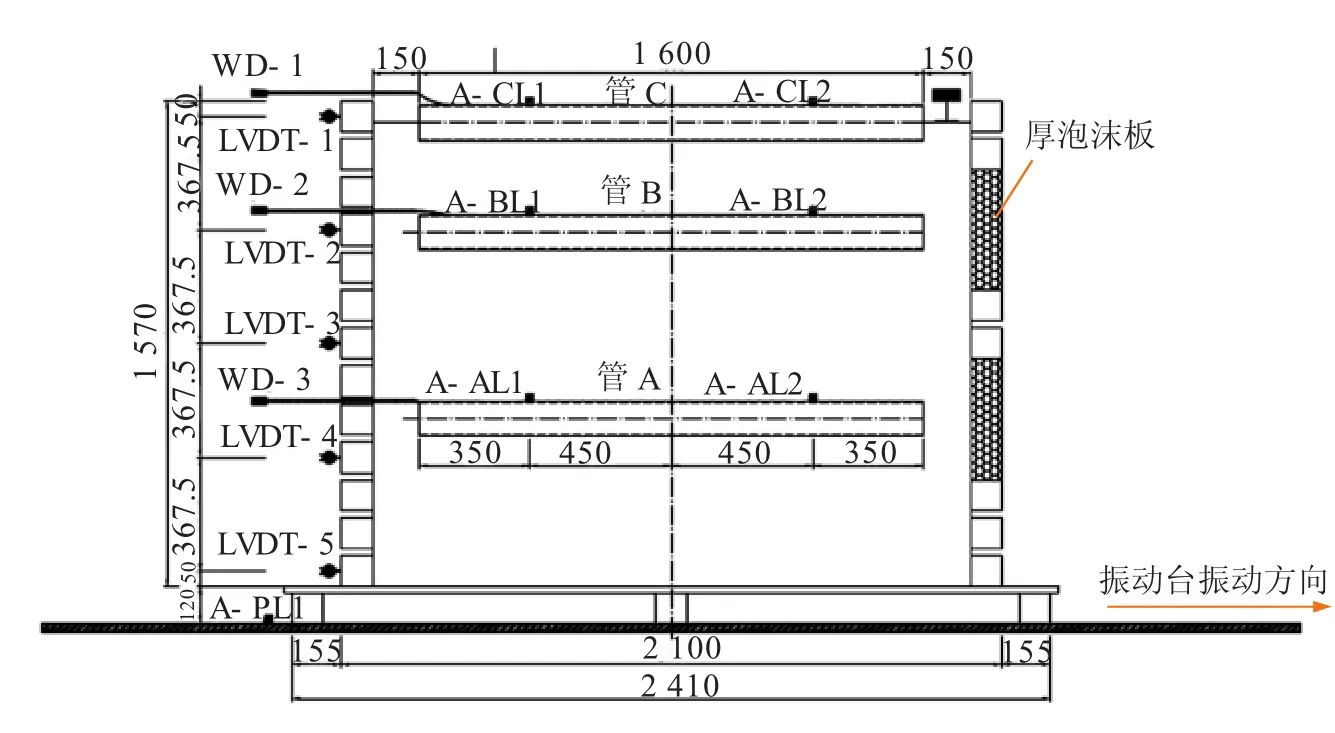
图2 模型场地传感器布置

图4 管外动土压力计布置

2.2 试验加载方案

简单来说，震中距在100～1000km范围内的地震称为近场地震，震中距＞1000km的地震称为远场地震，因此本文分别选用El Centro波（近场）和Kobe波（远场）作为输入原型波。由于试验相似比关系，振动台面输入的地震波波形必须按相似条件对原型波进行调整，使波形在时间坐标上压缩。在本文地震激励试验中，最小输入峰值0.04g，最大输入峰值0.68g，如表3所示。

3 试验结果分析

3.1 管-土接触面相对位移分析

由于土体与管道材料变形不一致，管-土界面之间常常有较大的剪应力，该剪应力即是管道受力的主要来源。土体属于松散介质，在振动受力过程中会产生压缩变形，对剪应力传递起缓冲作用，剪应力沿接触面的分布是不均匀的，导致接触面上的相对位移也不一致。此外，由于不同深度处的管-土间的初始剪应力不相同，导致不同埋深管道处的位移也会有差别。

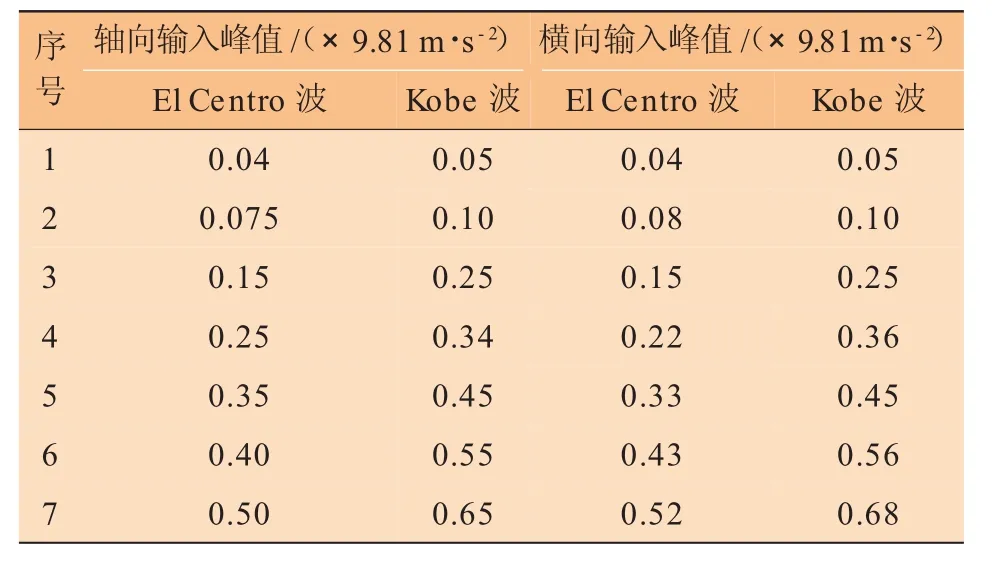
表3 试验输入工况

图5为El Centro波轴向输入下，管道及土体的位移时程曲线。

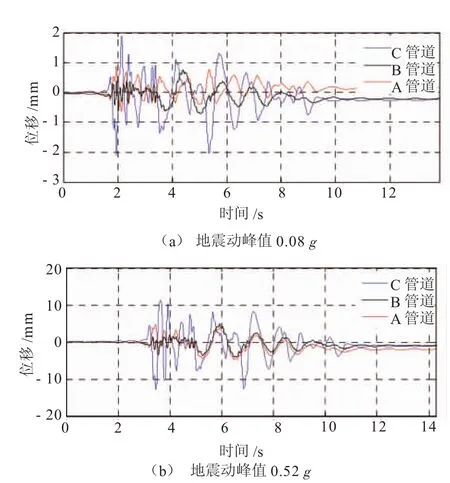
图5 ElCentro波作用下管道及土体的位移时程曲线

从图5可以看出，随着地震动峰值的增加，不同埋深的管道与土体间的相对位移都在增大。当地震动峰值为0.05 g时，埋深较大的A、B管道与土体间相对位移很小（＜0.2mm），接触面条件并未发生破坏，可以定义为未滑动状态；当地震动峰值达到0.08 g时，A、B管道与土体接触面开时出现微小相对位移，幅值达到0.8mm左右，管-土接触面开始发生破裂，接触状态改变，当管-土接触面破坏之后，管道与土体的变形不再协调，随着振动幅值的增大，二者将逐渐脱离。由于C管道埋深最浅，土体对管道的约束作用最弱，其接触面最易发生破坏，因而C管道与土体的相对位移最大。

另外，随着地震动峰值的增大，管-土接触面损伤逐渐积累。当地震动峰值增大至0.52 g时，A、B管道与土体间的相对位移接近4.6mm，管道应力增长缓慢，表明接触面间管-土的黏着力失去作用，管-土接触面基本处于自由状态，只存在稳定的摩擦力，管-土间剪应力传递值趋于恒定。

图6为Kobe波轴向输入下管道及土体的位移时程曲线。

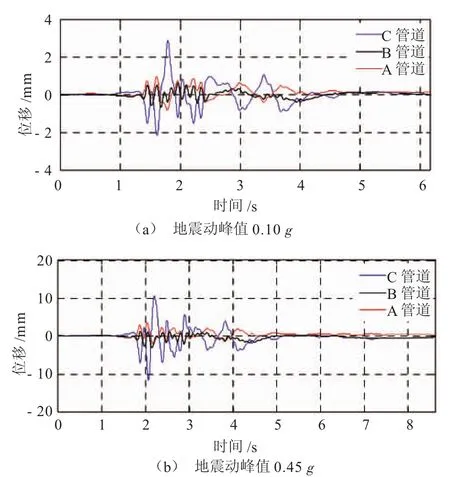
图6 Kobe波作用下管道及土体的位移时程曲线

通过比较El Centro波和Kobe波作用下的管道及土体的位移时程曲线发现，在远场地震动作用下，埋深较大的A管道与土体间的相对位移略小于B管道，即埋深越浅，管-土相对位移越大；而在近场地震动作用下，A管道却略高于B管道。此外，在近场地震动作用下，浅埋管道（即C管道）与土体间的相对位移也比远场地震动作用下高。

3.2 管道应变分布规律

管道应变分布可以直观反映其在地震中各位置处的受力状态，可以确定管道最不利受力位置和应变峰值，进而为设计提供参考和依据。在振动台试验中，应变片均沿管道长轴方向对称布置，以A管道为例，应变片的布设序号为S-AT1～S-AT10，距离管道左端依次为150、450、750、1050、1350mm。通过对不同峰值远场和近场地震动作用下的管道最大应变分析即可得到管道应变分布规律，如图7、8所示。

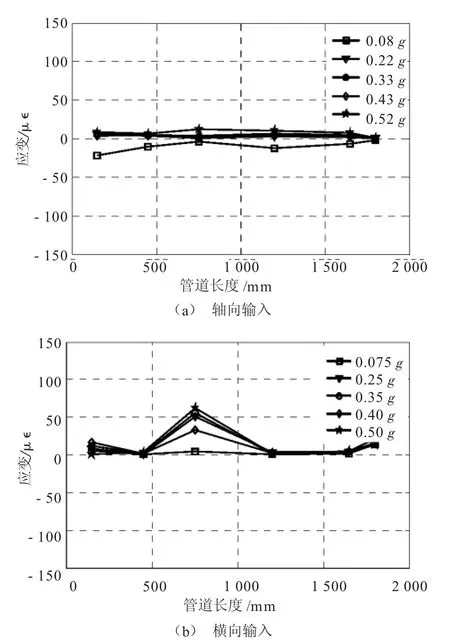
图7 ElCentro波作用下管道最大应变分布

从图7、8可以看出，轴向输入与横向输入对管道的影响程度不同，地震反应形式也不尽相同。通过比较可以发现，横向输入下管道应变响应明显大于轴向输入。远场地震作用时，横向下的峰值应变大约是轴向下的4倍左右；而近场地震动作用时，横向下的峰值应变达到轴向下的8倍以上，这说明近场地震动作用下管道所受作用力更大。

另外，在轴向输入下，土体对管道的作用通过接触面传递并施加于管道上，管道主要承受拉压作用，在地震动峰值较小时，管-土相互作用较弱，因而管道应变较小。而在横向输入下，管道明显受到了弯曲作用，即管道中间应变大，两端应变相对较小。由此可以推断，埋地管道的破坏主要取决于地震作用下土体的永久变形。

图8 Kobe波作用下管道最大应变分布

3.3 管道应变与土体位移的关系

在轴向输入下，由于远、近场地震动作用下的管道及土体的位移时程基本相似，此处仅以A管道为例，结合El Centro波作用下的管道应变分布及其所在位置处的管-土接触面相对位移情况，研究管-土相对位移与管道应变的关系，见图9。

从图9可以发现，当地震动峰值较小时，在轴向各个幅值输入下，管道应变时程和土体位移时程具有很强的相关性，即当管道与土体未发生相对位移时，管道应变与土体位移时程的规律基本一致，而当管道与土体的接触面发生破坏以后，土体位移将会偏离管道应变曲线，呈现增大趋势。当地震动峰值从0.15 g增加至0.52g的过程中，管道微应变从5με增大到16με，变化不大，原因在于管道应变主要由周围土体的相对位移引起，由于管道自重较小，周围土体对管道的约束作用较大，地震时管道的动力放大作用不明显。与此同时，由于管-土接触面的相对位移现象，土体位移的变化趋势比管道应变的变化趋势更显著。

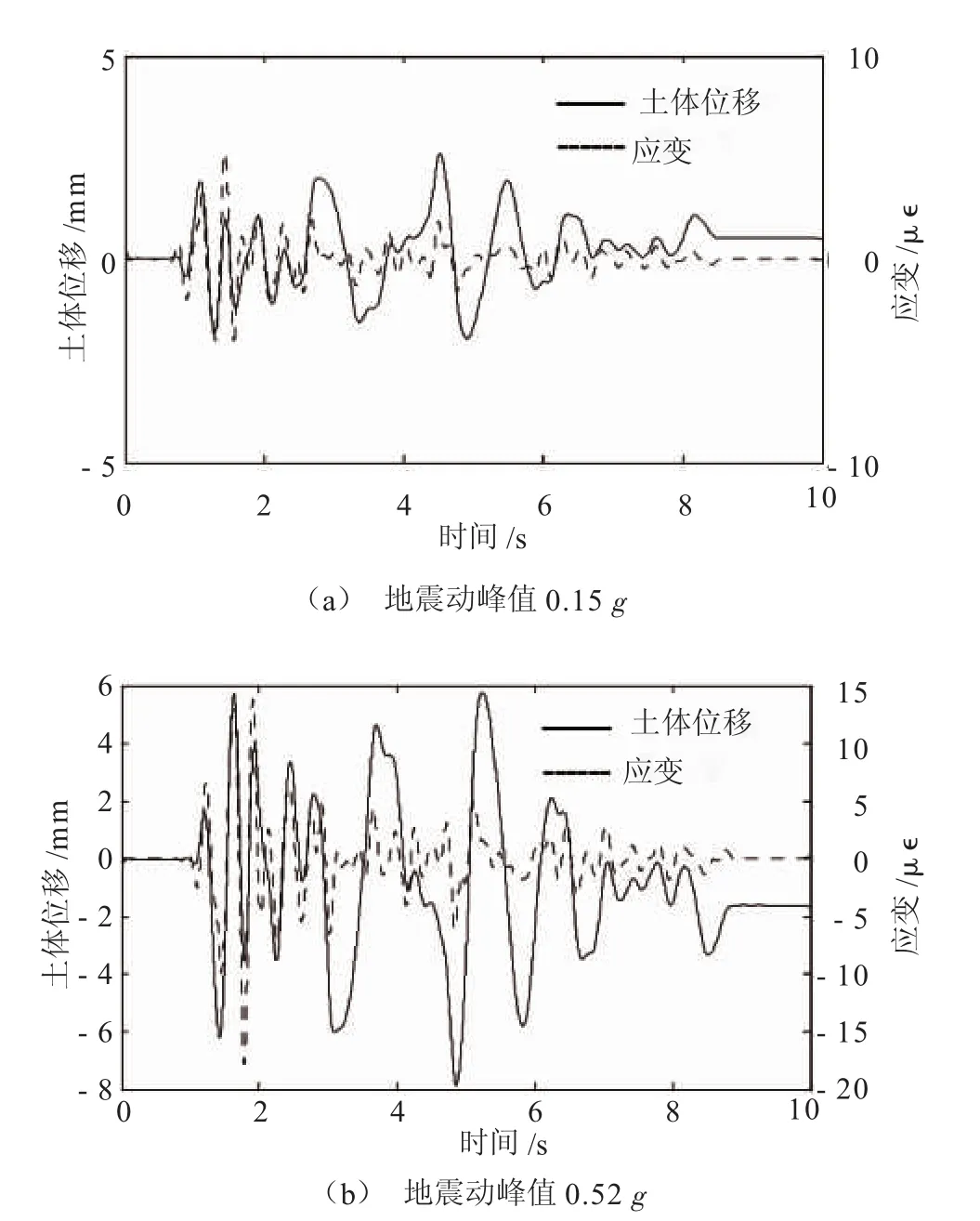
图9 ElCentro波作用下管道应变与土体位移时程对比

4 结论

基于Cauchy原理和Buckingham π定理进行了相似比设计，研制了刚度可调的叠层剪切箱，探讨了管道应变与土体位移的关系。通过对比分析，主要得到了以下结论：

（1）随着地震动峰值的增加，不同埋深的管道与土体间的相对位移都在增大。当管-土接触面发生破坏后，管-土间的变形不再协调。在相同峰值地震动下，管道埋深越浅，管-土间的相对位移越大，且近场地震动引起的位移量要高于远场地震动。

（2）横向输入下管道的应变明显大于轴向输入，而且近场地震动作用下管道所受的作用力更大。对比震害资料发现，埋地管道的破坏一般取决于地震动作用下土体的永久变形，管道与土体间的相对位移才是管道结构产生应变的主要原因。

（3）当管道与土体未发生相对位移时，管道应变时程和土体位移时程具有很强的相关性；当接触面发生破坏后，土体位移和管道应变不再同步。因此，土体本身的非线性变形和管-土接触面的非线性变化是影响管-土相互作用的决定因素。

[1]孙政策，段梦兰，张文，等.海底管道抗震设计的极限地震应力计算法[J].应用力学学报，2006，23（3）：440-446.

[2]张小玲，栾茂田，郭莹，等.地震荷载作用下海底管道的动力反应分析[J].岩石力学与工程学报，2008，27（S）：3 798-3 806.

[3]马良.海底管道抗震设计初探[J].中国海洋平台，1999，14（4）：26-29.

[4]许东禹，刘锡清.中国近海地质[M].北京：地质出版社，1997.

[5]MATSUBARA K，HOSHIYA M.Soil spring constants of buried pipelinesfor seismic design [J].Journal of Engineering Mechanics，2000，126（1）：76-83.

[6]PAULIN M J，PHILLIPS R，CLARKJ I，et al.Establishment of a full-scale pipeline-soilinteraction test facility and results from lateral and axial investigations in sand [C]//Offshore Mechanics and Arctic Engineering Conference.New York：American Society of MechanicalEngineers，1997：139-146.

[7]BRENNODDEN H，LIENG JT，SOTBERG T，et al．An energy-based pipe-soil interaction model[C]//Offshore Technology Conference．Houston：Society of Petroleum Engineers，1989：147-158.

[8]岳志勇，余轩凌，孙政策，等.引人惯性力影响的海底埋设管道的抗震设计方法[J].应用力学学报，2004，21（2）：110-114.

[9]HAI M，JUN C，JIE L I，et al.Shaking table test of soil-pipe dynamic interaction under non-uniform earthquake wave excitation[C]//5th China-Japan-US Trilateral Symposium on Lifeline Earthquake Engineering.Reston：American Society of CivilEngineers，2007：26-30.

[10]孟海，李杰，陈隽，等.地下管道-土体动力相互作用试验研究[J].工业建筑，2010，40（8）：91-94.

Experimental study on dynamic interaction between pipe and soil under earthquake excitation

CAO Wenran1，2，SHANG Ningning1，2，DENG Haifeng1，2，XU Hao1，2，MAO Tianyu1
1.CNPC Research Institute of Engineering Technology，Tianjin 300451，China
2.CNPC Key Laboratory of Offshore Engineering，Tianjin 300451，China

Earthquake shall be considered in the construction of submarine pipeline and the mechanism of pipe-soil interaction is the basis of seismic analysis of buried pipeline.On the basis of Cauchy’s principle and Buckingham π theorem，the similarity relation is calculated to ensure the similarity between the test model and the prototype.The laminar shear box is developed to simulate the boundary of soil.The method of measuring the relative displacement between pipe and soil is investigated，and the influences of buried depth，peak ground acceleration（PGA），far-field and near-field ground motion on the seismic behavior of buried pipeline are studied.The relative displacement of pipe-soil interaction and strain distribution along the pipe are also obtained.Then，the relationship between pipe strain and ralative displacement is analyzed.The test results show that the relative displacement between pipe and soil is the primary reason leading to the strain of pipeline structure，and the nonlinearity of soil itself and the pipe-soil interface is the key factor that influences the dynamic interaction between buried pipeline and soil.

shaking table；pipe-soilinteraction；interface slippage；pipe strain；soildisplacement

曹文冉（1984-），男，山东滨州人，工程师，2009年毕业于哈尔滨工业大学防灾减灾工程及防护工程专业，硕士，现从事海洋平台和海底管道研究工作。Email：caowenran@cnpc.com.cn

2017-04-27

10.3969/j.issn.1001-2206.2017.04.001

中国石油天然气集团公司科学研究与技术开发项目（2016A-1004）