ZTC14000/28/46型液压支架多目标优化设计

张豫龙

(天地科技股份有限公司 综合办公室，北京 100013)

ZTC14000/28/46型液压支架多目标优化设计

张豫龙

(天地科技股份有限公司 综合办公室，北京 100013)

针对带有套筒稳定机构的超前支护液压支架的套筒受力、支架重量相互矛盾的突出问题，在相同外载荷、最大工作高度下,以套筒机构受力绝对值之和、长度之和最小为目标函数，建立了多目标优化模型。使用NSGA-Ⅱ算法求解建立的模型，采用模糊集合理论的方法选择最优解，并在Matlab环境下编制计算程序，应用此程序优化ZTC14000/28/46超前液压支架参数，优化后伸缩杆受力减小136.21kN。ZTC14000/28/46在补连塔煤矿连续运行中未出现套筒机构断裂事故，为提高超前液压支架综合性能提供了有效途径。

超前液压支架；多目标优化设计；套筒机构；遗传算法

近年来，综采工作面回采巷道多采用超前液压支架进行超前支护，超前液压支架受超前支承压力影响，工作状况十分恶劣[1]，同时，工作面回采速度的提升和高产高效矿井的建设需要超前液压支架具有合理的支护能力、支护效率和可靠性[2-3]。

套筒稳定机构在使超前液压支架顶梁垂直升降的同时能保持梁端距恒定，同时套筒稳定机构具有结构简单、受力杆件少、支架重量轻、稳定机构占用空间小等优点，在煤矿综采超前支护中时有应用，但是目前对四连杆机构运动和力学性能研究已较为成熟，很少有套筒机构的研究，优化设计大多都是单目标。文献[3]分析了套筒机构的运动及受力，并且模拟了关键部位的应力，但是没有详细说明设计过程。本文主要探讨设计过程，并且建立套筒机构优化模型，并应用NSGA-Ⅱ算法求解，并使用模糊集合理论的方法选择最优解。本文分析以ZTC14000/28/46回风巷超前液压支架(图1)为例，该支架是由多组垛式液压支架组成，每组支架都由一个整体刚性顶梁和底座组成。

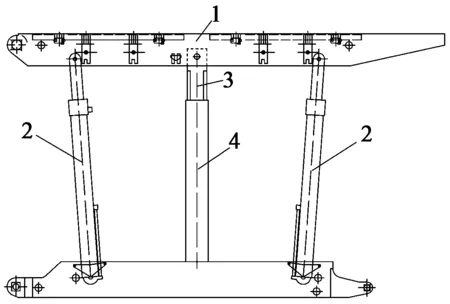
1—顶梁；2—立柱；3—伸缩杆；4—伸缩筒图1 带有套筒稳定机构的超前支护液压支架

1 设计过程及受力分析

本文将带有套筒稳定机构超前液压支架简化成如图2所示模型，设伸缩筒运动时伸缩杆的一侧紧贴伸缩筒，伸缩筒的边沿紧贴伸缩杆，伸缩杆与伸缩筒的中心线会有一个偏移角度φ，顶梁与伸缩杆铰接点产生水平位移x0。

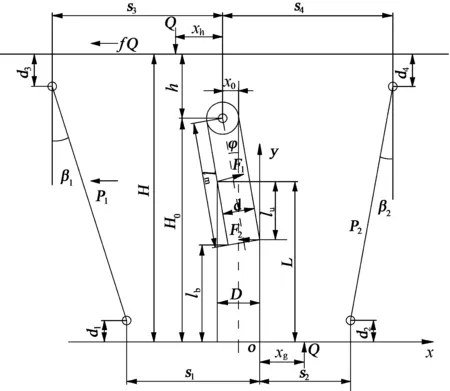
D—伸缩筒内壁纵向宽度；d—伸缩杆外壁纵向宽度；L—伸缩筒高度；lm—伸缩杆长度；lu—伸缩杆底部到伸缩筒上沿距离；lb—伸缩杆底部到底板距离；H0—铰接点高度；x0—铰接点水平位移；φ—偏转角度；s3，s4—铰接点与柱帽水平间距；s1，s2—铰接点与柱窝水平间距；d1，d2—底板与柱窝垂直间距；d3，d4—顶板与柱冒垂直间距；F1，F2—伸缩杆受力；P1，P2—立柱工作阻力；Q—支架工作阻力；β1，β2—立柱偏移角度；h—铰接点到顶板距离；H—支架高度；xh，xg—合力位置；f—摩擦系数图2 简化模型

支架设计过程如下：

(1)根据支架所用巷道情况，确定顶梁、底座总长，支架最低、最高高度。

(2)由于此类支架具有对称特性，在设计时考虑的对称结构参数有s1(s2)、s3(s4)、d1(d2)、d3(d4)，s2=s1-D，s3=s4。根据立柱缸径、顶梁和底座长度、最高和最低高度以及β角确定这些参数；10°≤βmax≤15°。

(3)根据最高、低高度设计lm，L，h；验算lu，防止支架在最高时伸缩杆从伸缩筒中脱落；验算lb，防止支架降不到最低高度。

(4)运动验算，检查干涉。

(5)受力验算，计算受力、强度等。

(6)优化设计。

将设计变量定为D，L，lm，s1，s3，以上步骤反复使用，直到使支架性能达到最优。

支架的运动和受力是设计支架的关键，通过分析结构可以得到如下运动方程：

(1)

(2)

(3)

(4)

结合上述分析的伸缩筒运动模型，可以得到如下受力方程：

(5)

(6)

顶梁垂直合力：

p1cosβ1+p2cosβ2+F1sinφ-Q=0

(7)

顶梁水平合力：

p1sinβ1-p2sinβ2+fQ+F2-F1cosφ=0

(8)

伸缩杆力矩平衡得：F1x=F2y

(9)

伸缩杆与顶梁铰接点到力F1的距离：

(10)

伸缩杆与顶梁铰接点到力F2的距离：

(11)

顶梁力矩平衡：

(12)

整个支架力矩平衡：

(13)

用解析法解方程(5)～(13)得方程组的解：

Q=p1cosβ1+p2cosβ2+F1sinφ

2 多目标优化模型

影响优化设计的主要因素有目标函数、变量和约束条件。此类支架中套筒机构是关键机构，该机构需要足够高的强度来承受超前支架顶梁与底座作用产生的力，为支架纵向和横向提供不同数值的弯矩和扭矩[4-5]，在设计时，考虑此处的受力最小最好；在满足承载能力的情况下，支架最轻最好，为了使支架最轻，将问题简化为使套筒机构长度、内外径之和最小。所以，最终的优化目标即为：

在最高位置时，为了防止伸缩杆从伸缩筒中脱落，应限制lu，即：

在最低位置时，为了防止支架降不到最低，应限制lb，同时伸缩杆与顶梁铰接处不能进入伸缩筒，即：

g2(x)lbmin=L-(D-dcosφmin)cotφmin>50

g3(x)=H0min>L+(200～350)

由于伸缩筒焊接存在焊接变形，为保证正常工作，将伸缩筒机构间隙定为10mm,即：

D=d+10

有些变量并不都是连续的，由于应用遗传算法产生的父代和交叉变异之后产生的子代，它们的变量的取值很可能是非整数的，例如精度等级为小数点后6位等，这就对加工精度提出很高的要求，如果人为对优化后的变量取整，这时很可能导致目标不是最优。本文将设计变量定为整数变量，处理方法如下：

即采用随机的方式，对整数变量的取值进行向上取整，或者向下取整。

3 使用NSGA-Ⅱ算法求解优化模型

NSGA-II算法是目前应用最广的多目标进化算法，其以进化算法为基础，通过并行操作不同种群个体进行运算，运算速度快、解集收敛性高。该算法降低了对种群个体初值的要求，降低了个体初值对运算结果的影响。该算法可以在进化操作的过程中针对不同种群设置不同的约束条件，在提高效率的同时还能确保模型的收敛性，保证模型有解[6-7]。

使用NSGA-II算法求得的是多目标优化模型的pareto集，还需要分析其中的最优解，人工挑选pareto最优解受人的主观因素影响较大，会影响挑选的准确性，而采用结合模糊集合理论的pareto集选优方法不受主观因素的影响，选优结果较为可靠[8-9]。多目标优化模型运算及选优过程见图3。

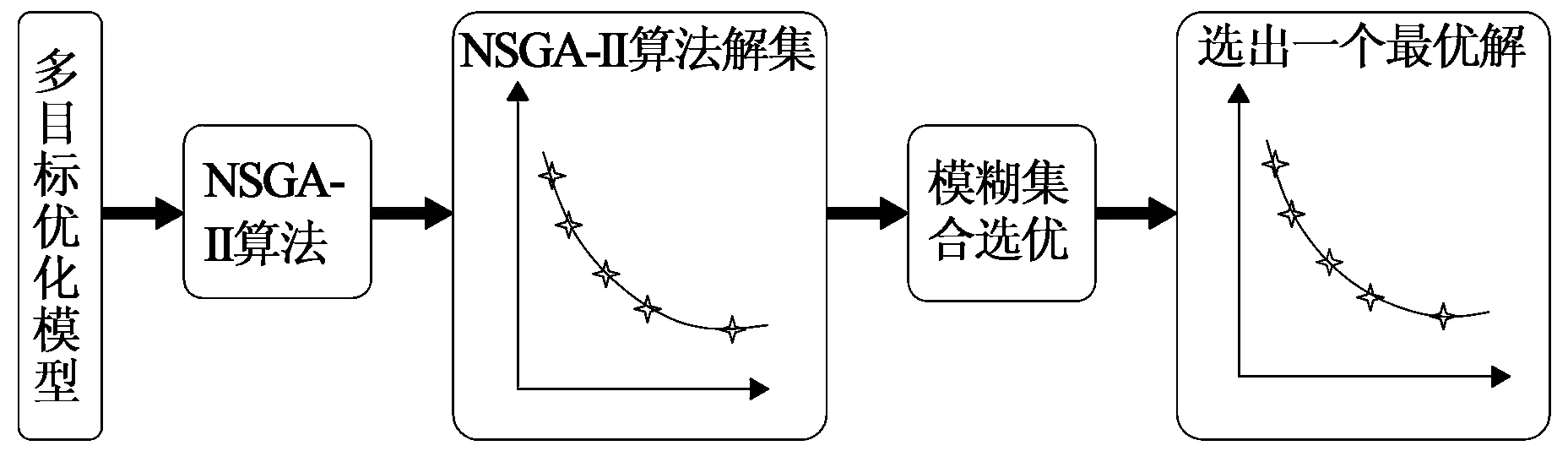
图3 多目标求解及选优过程示意

定义成员函数μi表示一个解的第i个目标值所占的比重：

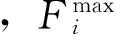
式中，Mp为pareto解集中解的数量；NObj为优化目标的数量，μk值与解的综合性能成正相关。Pareto解集中μk值最大的解即为最优解。

4 实例计算

以ZTC14000/28/46型超前液压支架为例，该支架主要参数：D=490～590mm，L=490～590mm，lm=800～920mm，s1=400～500mm，s3=750～850mm，其余参数视现场使用情况和经验而定。使用NSGA-Ⅱ算法求解，设种群规模为50，迭代100次，图4为迭代完成后所得的pareto前沿。

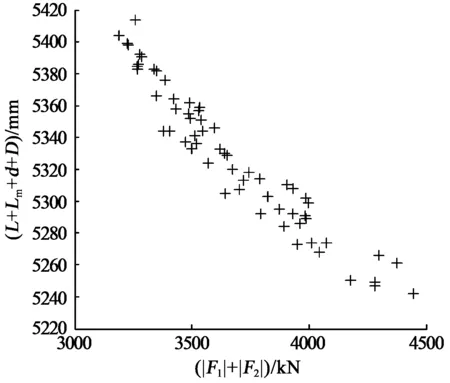
图4 pareto前沿

表1为5种设计变量的值，表2为与变量对应的伸缩杆受力值。表中伸缩杆受力值是伸缩杆处于最大伸长量，顶梁与顶板的摩擦系数取0.2时计算得出。由表1和表2可知，优化后超前液压直接的伸缩筒受力和长度之和都较优化前小。应用前述选优方法在优化解集中选择最优解，验算表1和表2中5组数据，第1组数据μk最大，最大值为0.256，即第1组数据即为最优解，将最优解与优化前超前支架受力状况进行对比分析，分析结果如图5所示。所选的最优解与优化前相比受力之和降低了136.21kN，长度之和下降了16mm。

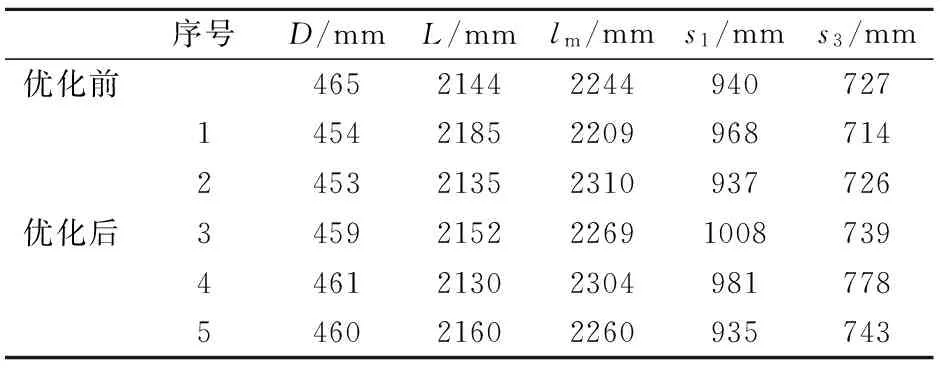
表1 设计参数

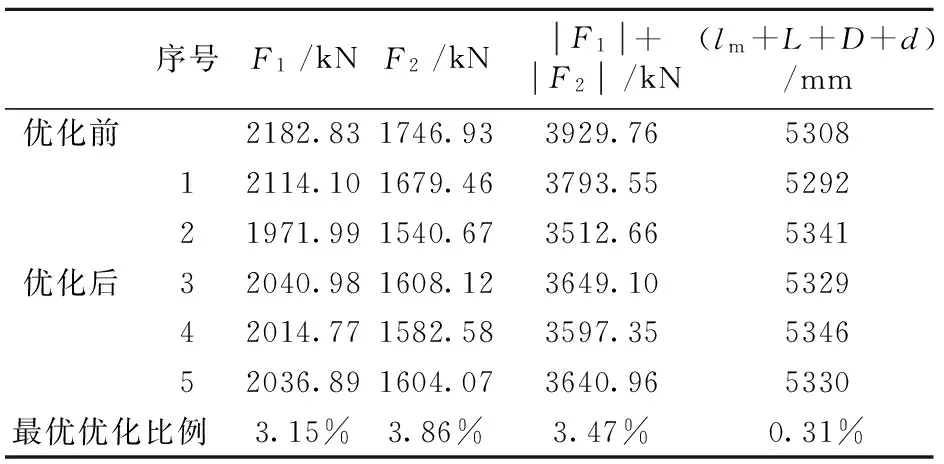
表2 结果对比

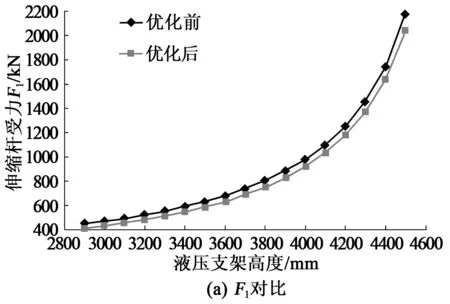
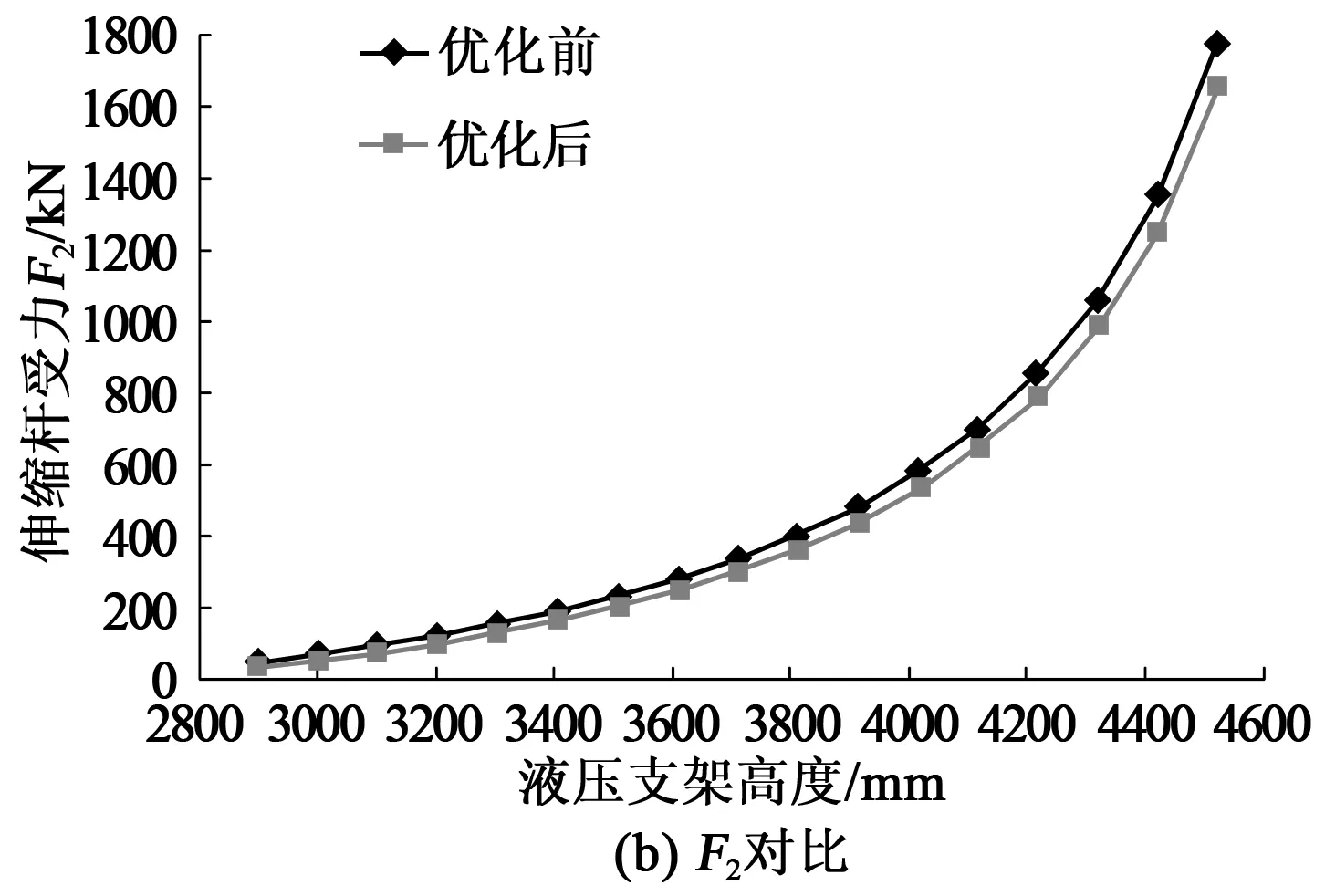
图5 优化前后伸缩杆受力F1与F2对比

5 结 论

探讨了伸缩筒稳定机构超前支架的设计过程，从结构出发，分析了支架受力，建立了多目标优化模型，选择了优化参数，使用NSGA-Ⅱ算法求解优化模型，采用结合模糊集合理论的pareto集选优方法挑选最优解并进行了实例计算，对带伸缩筒稳定机构的超前液压支架进行了优化设计，设计结果具有极强的使用性，可满足实际应用要求。优化后的液压支架在缩短伸缩筒长度的同时降低了支架受力状况，提高了支架的可靠性。

[1]张德生，牛艳奇，孟 峰.综采工作面超前支护技术现状及发展[J].矿山机械，2014，42(8)：1-5.

[2]曾明胜.深部综放工作面巷道强力超前支护系统设计[J].煤炭科学技术，2011，39(6)：15-18.

[3]王国法.高端液压支架关键技术研究与产业化进展[J].煤炭科学技术，2011，39(4)：20-23.

[4]牛艳奇，刘 伟，张德生.ZTC16000/29/45型液压支架套筒机构有限元分析[J].矿山机械，2015，43(8)：31-34.

[5]赵建武，桑盛远.回风巷自移式超前支护支架组的研制[J].煤矿机械，2010，31(3)：25-27.

[6]牛艳奇，刘 伟，张德生.基于NSGA-Ⅱ算法的超前液压支架多目标优化设计[J].机械强度，2015，37(3)：450-455.

[7]郑金华.多目标进化算法及其应用[M].北京：科学出版社，2007.

[8]Deb K，Pratap A，Agarwal S，et al.A fast and elitist multi-objective genetic algorithm：NSGA-II[J].IEEE Transactions on Evolutionary Computation，2002，6(2)：182-197.

[9]成晓升.基于NSGA-II的齿轮减速器多目标优化研究[J].机电工程，2014，31(5)：568-572.

[责任编辑：徐亚军]

Multi-objective Optimization Design of ZTC14000/28/46 Hydraulic Support

ZHANG Yu-long

(General Office，Tiandi Science & Technology Co.，Ltd.，Beijing 100013，China)

In order to solve the paradox problems of sleeve stress and support height of advance supporting hydraulic support with sleeve stability structure,under the same loading and the maximal working height，and it takes sum of absolute value and sum of length of sleeve structure stress as objective function，then multi-objective optimization model was built，and the model was solved by NSGA-Ⅱalgorithm，the optimal solution was selected with fuzzy set theory，and calculation program was complicated under Matlab environment,the parameters of advance hydraulic support ZTC14000/28/46 were optimized by the program,then expansion link stress decreased 136.21kN.The sleeve structure cracking accident had not appeared during ZTC14000/28/46 continuous working time in Bulianta coal mine，it provided more effective method for combination property improving of advance hydraulic support.

advance hydraulic support；multi-objective optimization design；sleeve structure；genetic algorithm

2017-04-20

10.13532/j.cnki.cn11-3677/td.2017.04.010

国家重点基础研究发展计划(973计划)：深部围岩自适应支护原理及系统创成理论(2014CB046302)

张豫龙(1978-)，男，山西昔阳人，工程师，现任天地科技股份有限公司综合办公室副主任。

张豫龙.ZTC14000/28/46型液压支架多目标优化设计[J].煤矿开采，2017，22(4)：35-38.

TD355.41

A

1006-6225(2017)04-0035-04