开关磁阻电机磁密及铁耗分析

高旭东，王希凤，曹珊珊，张嘉航

(1.黑龙江工程学院 电气与信息工程学院，黑龙江 哈尔滨 150050；2.黑龙江工程学院，黑龙江 哈尔滨 150050)

开关磁阻电机磁密及铁耗分析

高旭东1，王希凤1，曹珊珊1，张嘉航2

(1.黑龙江工程学院 电气与信息工程学院，黑龙江 哈尔滨 150050；2.黑龙江工程学院，黑龙江 哈尔滨 150050)

以1台三相、12/8极、3 kW开关磁阻电机(SRM)为样机，在电机电磁场基础理论及条件假设的基础上，建立场-路耦合的电机电磁场计算模型，利用时步有限元法对电机工作在额定负载工况下的运行情况进行仿真和数值求解，进一步分析电机气隙磁密的分布情况和谐波含量，并对电机定、转子铁心磁密进行研究。在此基础上，通过将电机铁心分段，分析额定负载状态下电机不同铁心段的铁心损耗，并得出一些有益的结论。

开关磁阻电机；时步有限元法；气隙磁密；铁心磁密；铁心损耗

开关磁阻电机(Switched Reluctance Motor,SRM)是随着电力电子技术的不断发展而出现的一种特种电机，其机电一体化程度较高，电机结构简单，制造成本低廉，启动性能好，运行效率高，并且控制系统稳定性良好，因此，SRM在许多领域都得到了良好的应用[1-2]。但是，由于其内部的磁路具有非线性的结构，且控制电路的开关性随周期变化，使其内部的电磁性能及运行性能异于普通三相电机。因此，对SRM瞬态磁密及铁耗进行分析计算，以了解其各项性能，就显得尤为重要。

在SRM瞬态性能分析方面，国内外学者进行了深入研究，主要有参数法与有限元法(简称FEM)。

参数法主要描述电机内部绕组磁链与绕组电流之间的关系，该方法分为有限性、准线性和非线性3种不同的数学模型[3]。J.M.Stephenson和J.Corda提出了非线性此参数法，该方法所需数据较少，对计算精度造成影响[4]。T.J.E.Miller和McGilpM提出了快速非线性法。该方法忽略了定子绕组之间的电感耦合作用，使计算精度受到影响[5]。等效网络法是另一种开关磁阻电机的分析方法，该方法考虑的电机磁路的非线性及多相电下磁路之间的影响，但在计算过程中做了大量的近似和等效，会对结果造成误差[6-7]。

FEM是将连续的求解域离散为一组单元的组合体，在每个单元内假设的近似函数来分片地表示求解域上待求的未知场函数，从而使一个连续问题变成离散问题。该方法仍需要对电机进行一定的假设，但精度大大提高。

本文选取FEM，结合场-路耦合的分析，将外电路与FEM结合，大大提高了二维瞬态电磁场的计算精度[8-10]。选取1台三相SRM样机进行分析与计算，考虑饱和以及谐波等影响因素，基于时步有限元计算法对电机进行建模及仿真计算，得出其磁密及铁耗的计算数值，对了解SRM性能极具价值且可为后续温度场计算奠定基础。

1 SRM二维有限元分析

1.1 时步有限元法的数学模型

将转子电路方程与电磁场方程联合，并进行离散化处理，可得到SRM二维时步有限元场-路耦合方程，如式(1)所示。

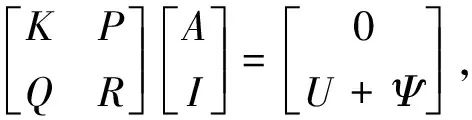
(1)

(2)

(3)

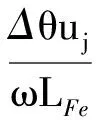
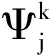
转子运动的耦合通过有限元前处理的网络剖分来实现。剖分时，气息作为单连通域，每次根据转子的运动，重新形成初始的网络数据进行剖分，这样，每次的剖分都相对独立，不受以往的网格限制，只需要转子位置的信息。

1.2SRM二维模型建立

本文选取的SRM具体参数如表1所示。

表1 电机参数

根据表1中数据，可对电机进行二维模型的建立。模型如图1所示。

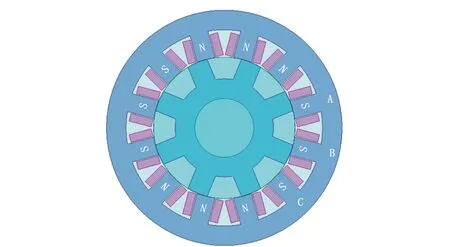
图1 SRM二维模型

本文所选用电机采取不对称绕组连接方式，定子极磁场如图1中标注所示，为S-S-S-N-N-N- S-S-S-N-N-N，电机内部的磁场不对称，存在相邻极性相同的情况。由于结构的对称性，本文采取1/4模型对SRM进行分析和计算，且为分析其径向各个区域磁密及铁耗的分布情况，对电机进行区域划分，如图2所示。

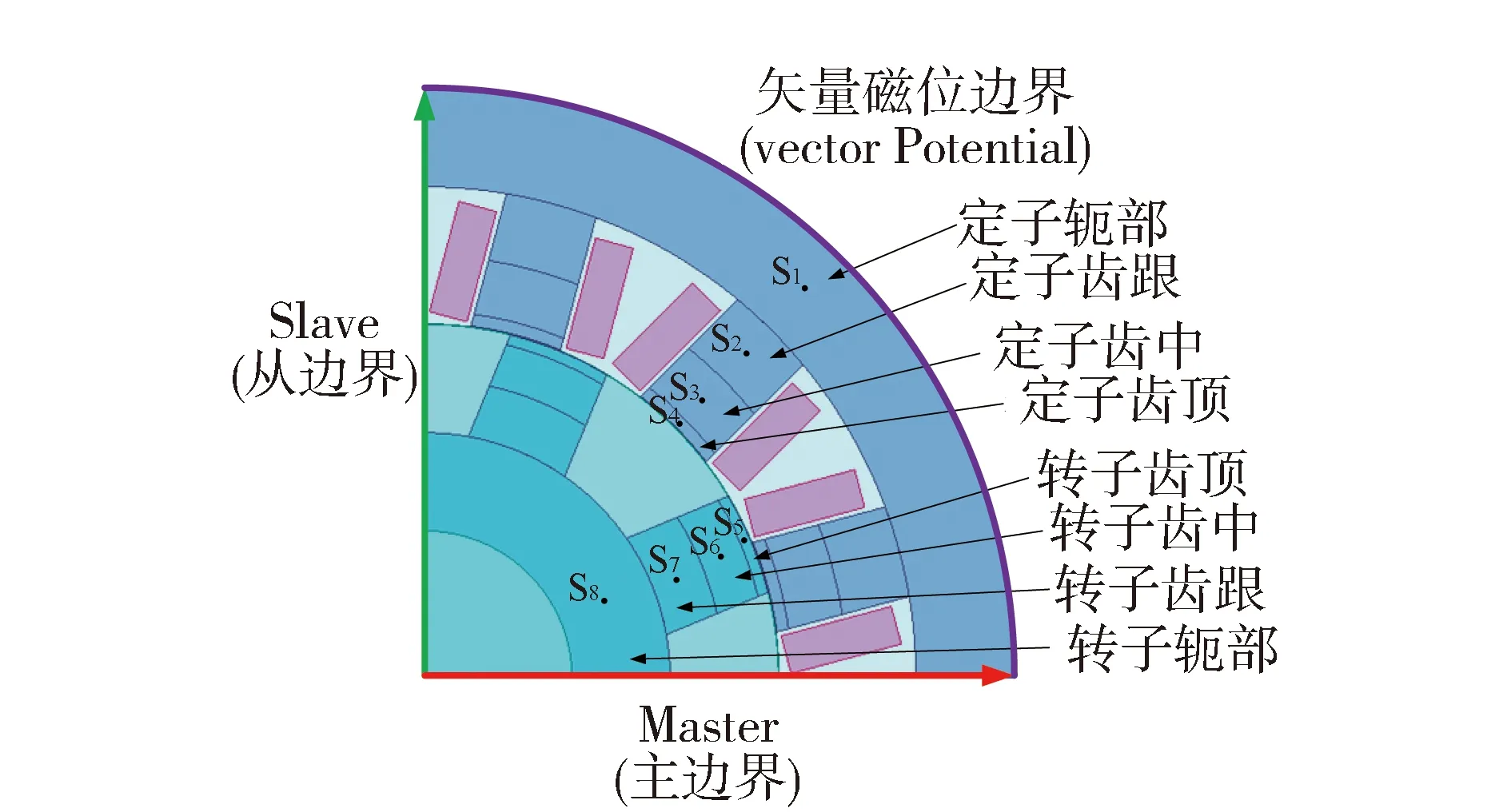
图2 SRM计算模型及边界条件

由图2可知，本文将SRM定、转子铁心分为8个区域，沿径向从外向内依次为定子轭部、定子齿跟、定子齿中、定子齿顶、转子齿顶、转子齿中、转子齿跟和转子轭部，其中，S1～S8为各个区域中的一点。

为了分析计算方便，做如下假设[11-13]：

1)忽略电机端部的磁场效应，将三维问题简化成二维问题；

2)电机外部磁场占比较小，可忽略不计；

3)定、转子铁心各向同性，磁化曲线为单值；

4)不计磁场交变在导电材料中的涡流反应。

根据假设条件，需要对SRM求解模型进行边界条件设置，如图2所示。

由于此处选取1/4模型，因此，需对电机施加主从边界条件，同时对求解区域边界施加矢量磁位边界条件。在采用矢量磁位A分析电机磁场时，仅有Az分量，并满足非线性泊松方程，其边值问题为

(4)

式中：Jz为传导电流密度，μ为磁导率。

1.3 磁密及铁耗

磁密也就是磁通密度，是指垂直通过单位面积的磁力线的数量，也称磁感应强度。在电机运行中，由于磁场分布复杂，因此，很难得到磁密随时间变化的曲线，只能通过磁场分布情况，得到铁心上每个小单元的磁密波形。磁密可表达为

B(t)=Bx(t)ex+By(t)ey.

(5)

式中:ex和ey分别表示径向和切向。在考虑磁密时，主要考虑径向和切向两个方向。

铁耗是描述电机性能的重要参数之一，铁耗的大小严重影响电机的制造成本和运行效率。目前已有大量学者对电机铁耗进行研究[14-16]，随着研究的不断深入，A.Bertotti提出的交变损耗分离模型得到最广泛的认可，并延续至今。即将损耗分离为3个部分，分别进行计算，并相加得到总损耗值。这3部分分别为磁滞损耗、涡流损耗和附加损耗，该方法可表达为

PFe=khfB2+kef2B2+kaf1.5B1.5.

(6)

式中:等式右侧从左至右3个式子依次为磁滞损耗、涡流和附加损耗；kh，ke和ka分别为相应的损耗系数；f为频率(Hz)；B为磁通密度幅值(T)。

考虑到电机在实际铁磁材料中引起的磁路非线性和绕组分布，特别是定子铁心开槽作用引起的谐波响应，可将谐波损耗计入A.Bertotti交变损耗分离模型，因此，式(6)可改写为

(7)

式中:v为谐波次数，当v=1时为基波；fv为v次谐波频率(Hz)；Bv为v次谐波磁幂幅值(T)。

2 SRM驱动电路模型

SRM的驱动电路是基于电力电子技术设计而成，它由若干电力电子开关器件组合而成。各个器件在控制器指令下按照一定次序开通和关断，以实现对SRM的控制。

本文所用控制方式的等效电路主电路如图3所示。在该图中，采用可控电压开关S37～S42与二极管D25～D36反并联的方式来等效实际APC控制电路中的电力电子开关器件，且需设置可控电压开关的开通电压和关断电压，通过对可控电压开关施加脉冲电压信号来控制其开通关断。其中，LA，LB和LC为定子绕组漏感，RA，RB和RC为SRM定子绕组电阻，LPhaseA，LPhaseB和LPhaseC为等效的三相定子绕组。

图3 等效驱动电路

图3中等效电路主电路的控制电路如图4所示。其中，R1，R2和R3为限流电阻，V1，V2和V3为脉冲电压源，其脉冲信号的大小和作用时间与电机旋转位置和转速有关，通过控制信号的导通角和信号周期实现SRM控制。

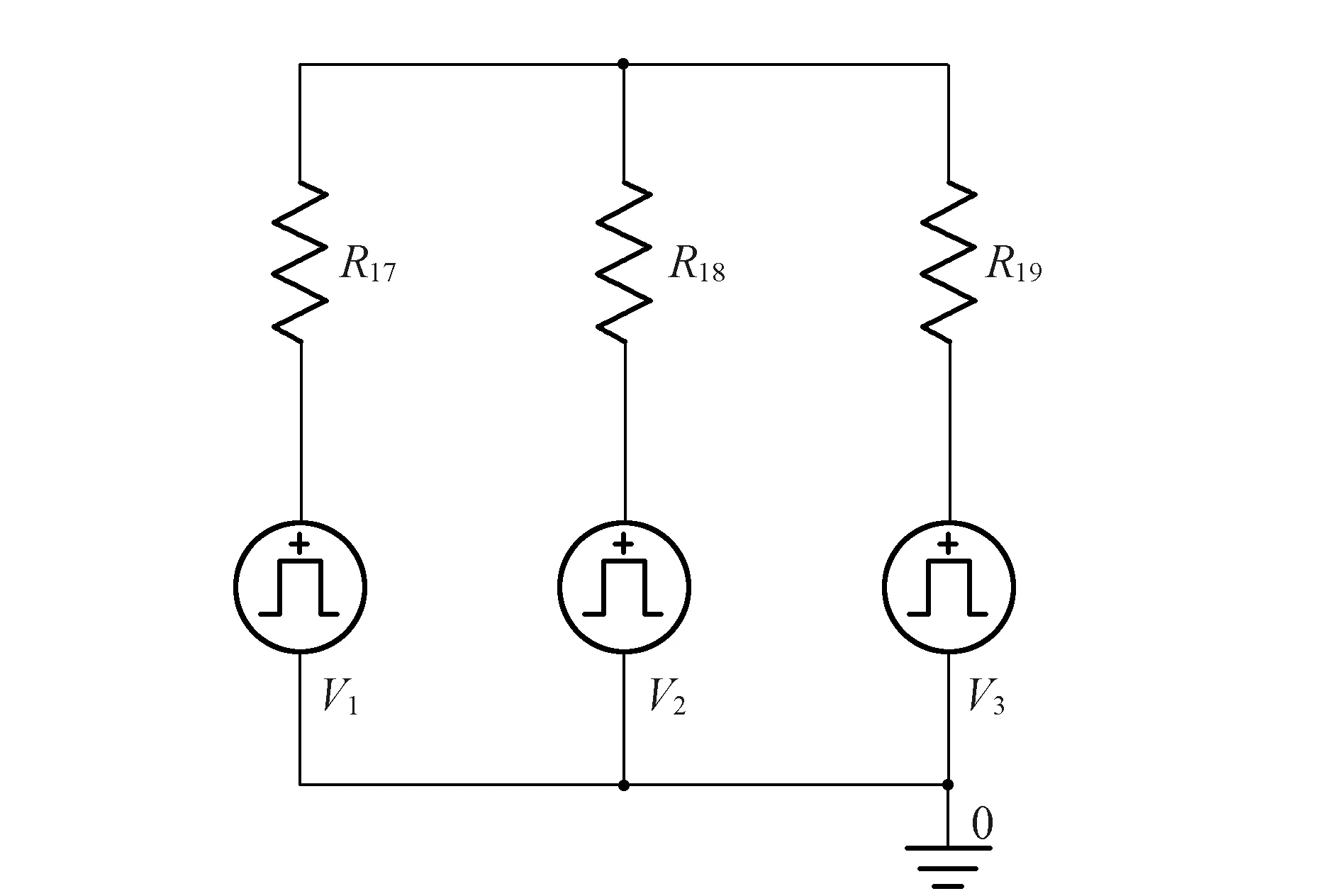
图4 等效驱动电路控制电路

3 SRM磁场分布及磁密

3.1SRM磁场分布

本文所用SRM的磁场分布如图5所示。

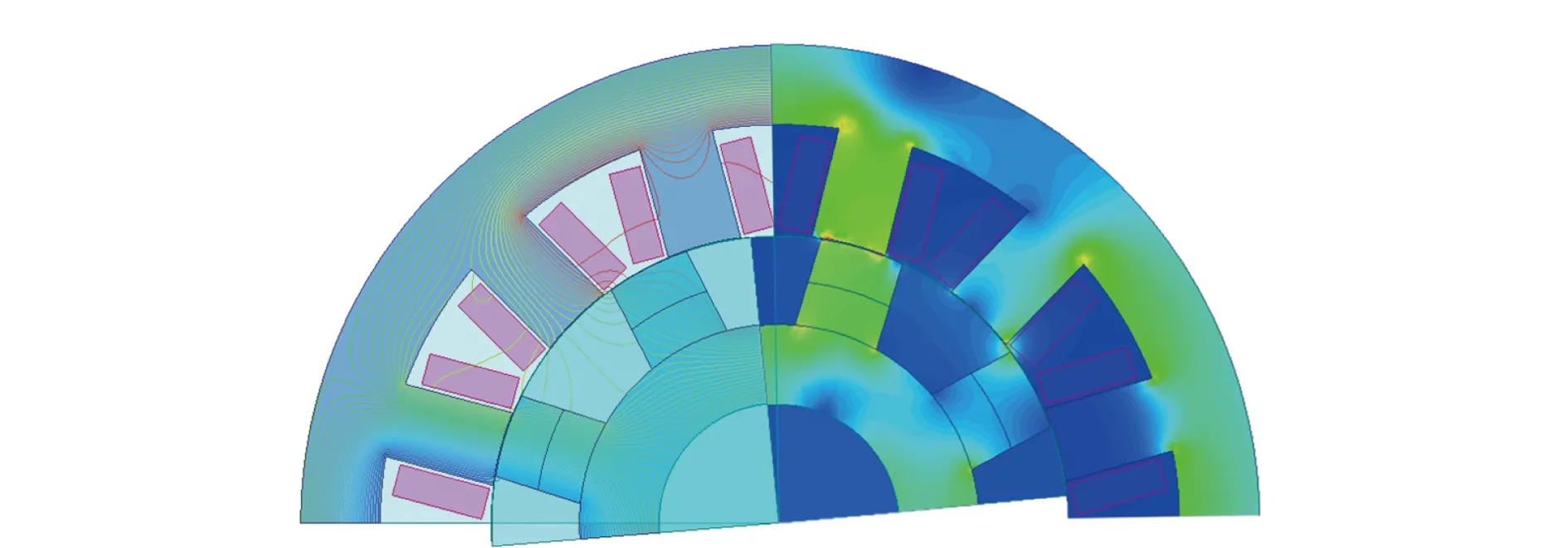
图5 SRM磁场分布

图5中左半部分为开关磁阻电机磁场磁力线分布图，右半部分为SRM磁通密度云图。由于SRM定、转子极数不同，电机定转子磁极交错对准与错开，导致定转子之间磁阻不断变化。SRM遵循“磁阻最小原理”，即磁通总要沿着磁阻最小的路径闭合，而具有一定形状的铁心在移动到最小磁阻位置时，必使自己的主轴线与磁场的轴线重合。因此，随着定子绕组内电流相位的变化，定子磁场逆时针旋转，致使转子随定子磁场转动。从图中可以看出，磁力线沿着磁阻最小处(定、转子齿部轴线重合处)闭合，该处磁密也为最大值。

3.2 SRM气隙磁密

图6为角度位置控制(APC)下SRM磁链波形图，可以看出，稳定运行时，SRM磁链为三角波，并且成周期性变化。可以通过控制外电路控制角来控制磁链的大小，控制角开通时，磁链上升，控制角关断时，磁链下降。

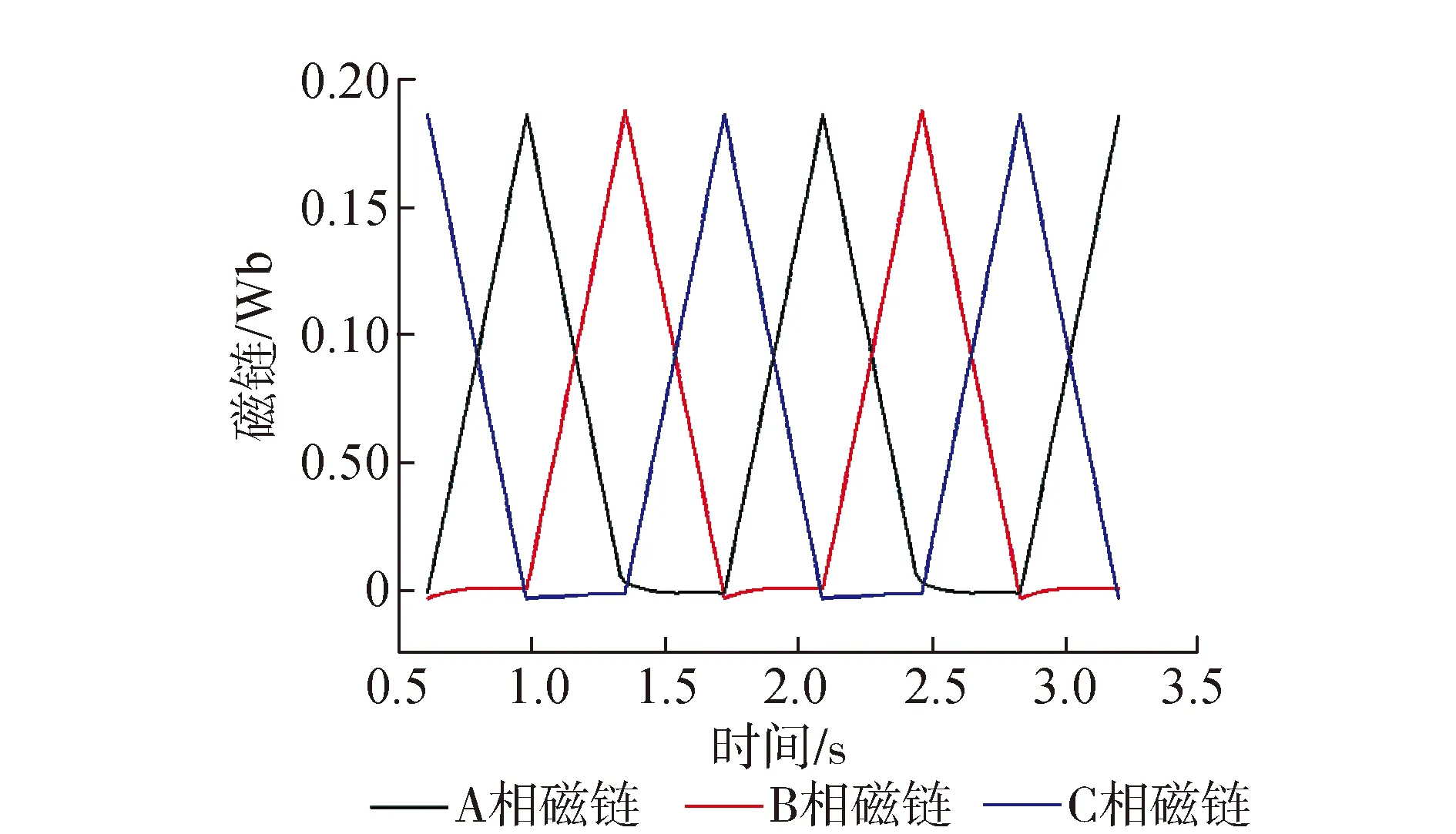
图6 SRM磁链分布

图7为SRM的1/4气隙磁密沿气隙周向分布图，从图中可以看出，由开关磁阻电机工作原理可知，开关磁阻电机气隙磁密非正弦。在定转子齿部交合处，气隙磁阻最小，磁密达到最大值，约为2.022 8 T。

对磁密进行谐波分解，可得到图8所示柱状图。从图中可以看出，基波磁密占比最大，幅值约为0.812 T，其他次数谐波依次减小，无偶次谐波。由于气息磁密非正弦趋势明显，因此，磁密谐波含量较大。

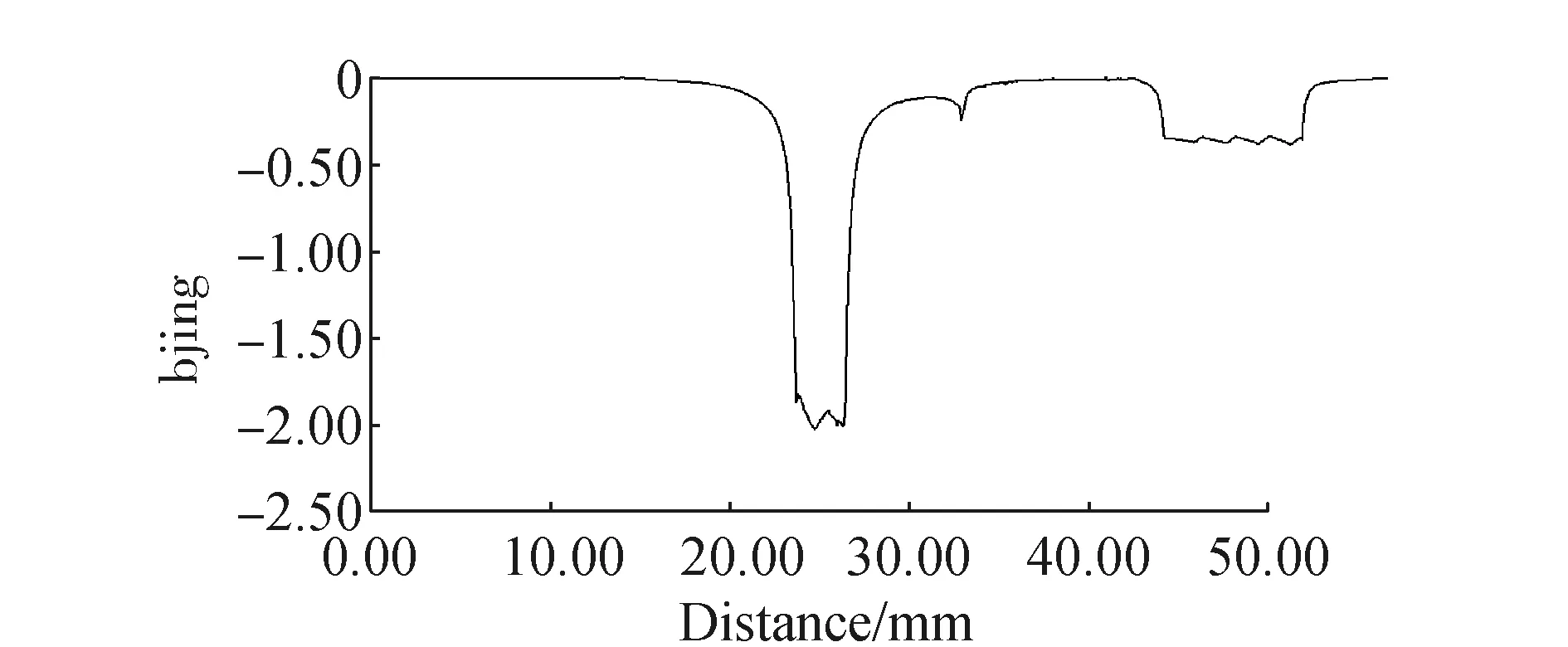
图7 1/4气隙磁密分布

图8 气隙磁密谐波分布

3.3 SRM铁心磁密

由前述可知，SRM铁心磁密为非正弦，且在定、转子齿部，铁心磁密主要为径向分量，在定、转子轭部，铁心磁密主要为切向分量。在前文中，将定、转子铁心分段，分别为定子轭部、定子齿跟、定子齿中、定子齿顶、转子齿顶、转子齿中、转子齿跟和转子轭部，在每个铁心段的中心圆上取一点，依次为S1～S8，观测每点的磁密，以该点磁密代替该点所在铁心段的磁密。铁心各部分磁密幅值如表2所示。

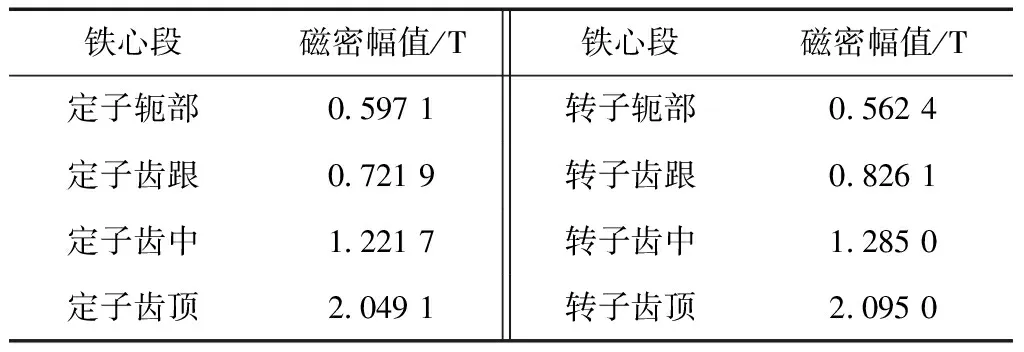
表2 铁心段磁密幅值

从表2可以看出，定、转子铁心齿顶部磁密幅值最大，分别达到2.049 1 T和2.095 0 T。这是由于磁阻最小工作原理使得磁力线经过定子齿顶，到气息，再到转子齿顶，形成闭合回路，因此，这部分磁密较大。轭部磁密幅值最小，达到0.597 1 T和0.562 4 T。

4 SRM铁耗分析

在前文分析了定、转子磁密的基础上，结合A.Bertotti交变损耗分离模型的公式，利用有限元分析法，对电机铁耗进行分析。

本文对SRM工作在额定负载下的铁心损耗进行分析，可得各个铁心段铁心损耗趋势如图9所示，具体数值及占比如表3所示。

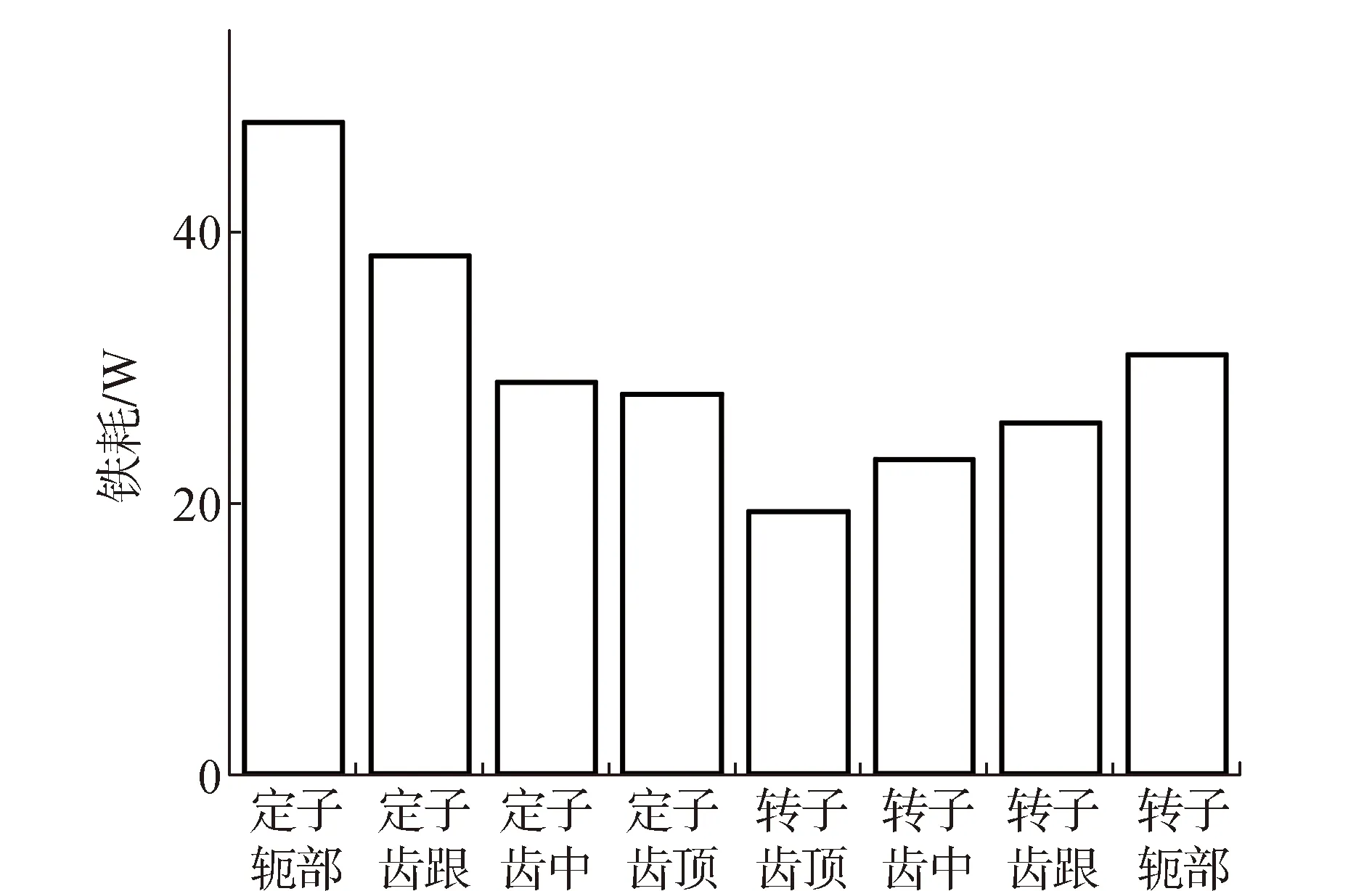
图9 区域铁耗分布

可以看出，定、转子轭部铁耗占比非常大，其中定子轭部铁耗为48.3 W，占比总铁耗的19.8%，转子轭部铁耗为31.1 W，占比总铁耗的12.7%。定、转子齿顶铁耗占比最小，其中，定子齿顶铁耗为28.2 W，占比总铁耗的11.5%，转子齿顶铁耗为19.6 W，占比总铁耗的8.1%。总体上来讲，定子侧铁耗明显大于转子侧铁耗，这是由于磁场在定子侧产生，而在转子侧仅为定子产生的磁场构成回路，因此，铁耗略小于定子侧。

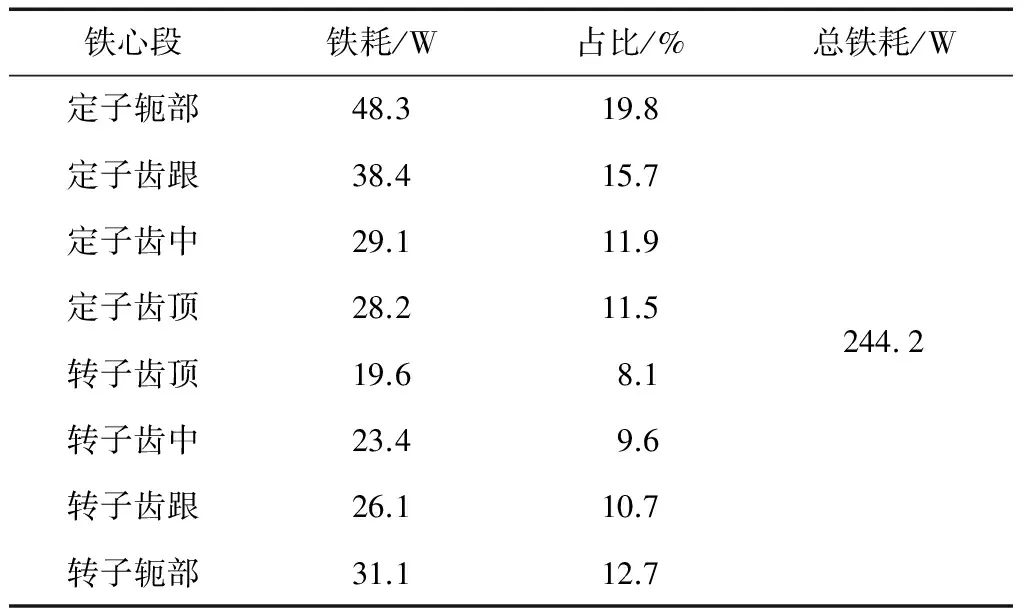
表3 区域铁耗数值及占比

5 实验对比

为了验证计算结果的准确性，对本文所研究SRM样机进行测试实验，得到测试结果如表4所示。

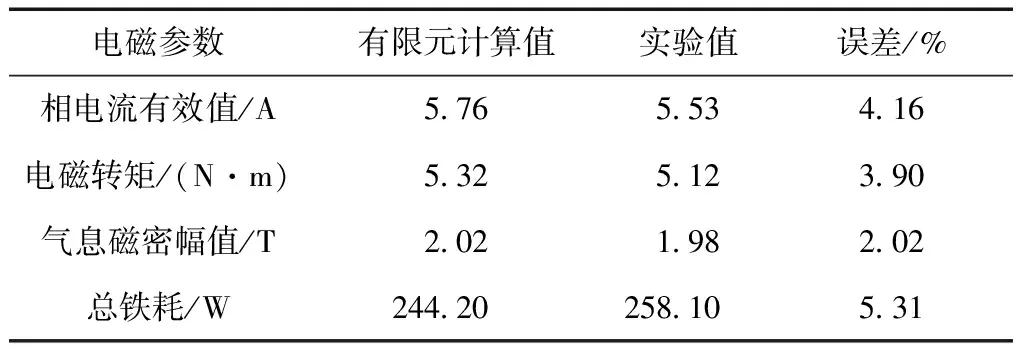
表4 计算值与实验值对比

经过实验值与有限元法计算值的对比，可以看出，各个参考量的值有一定误差，但误差均在合理范围内，验证了本文计算的准确性。

6 结 论

本文选取1台3 kW的开关磁阻电机，对其进行有限元分析，分别计算其磁密及铁耗的具体数值，并进行分析，可得如下结论：

1)SRM磁密为非正弦趋势，在定、转子齿部交合处，气隙磁阻最小，磁密达到最大值，且谐波含量较大；

2)在SRM铁心部分，定、转子齿顶磁密幅值最大，轭部磁密幅值最小；

3)SRM铁耗主要集中在定、转子轭部区域，该部分占比为总铁耗的32.5%，而定、转子齿顶处的铁耗最小，占总铁耗的19.6%，其中，定子侧铁耗大于转子侧铁耗;

4) 将FEM计算结果与实验进行对比分析，可知其误差在合理范围内，验证了本文计算方法的正确性。

[1] 吴红星.开关磁阻系统理论与控制技术[M].北京：中国电力出版社，2010.

[2] 王宏华.开关磁阻电动机调速控制技术[M].2版.北京：机械工业出版社，2014.

[3] PRABHU V Vasan，MAHESH K S，RENUKA C. Simulation of switched reluctance machine for linear and nonlinear model[J]. IEEE ICCCET, 2011, 18: 333-339.

[4] STEPHENSON J M, CORDA J. Computation of torque and current on double Salient reluctance motors with nonlinear magnetization data[J]. IEE Proc, 1979: 392-397.

[5] MILLER T J E. Nonlinear theory of the switched reluctance motor for rapid computer-aided design[J]. IEE Proc, 1900: 337-347.

[6] 童怀.开关磁阻电机等效网络模型的降阶处理方案[J]. 电工技术学报，2000，15( 1):30-35.

[7] MARCO Franke, OLIVER Punk, MICHAEL Brutscheck. Magnetic equivalent circuit modeling of rolling rotor switched reluctance motors[J]. IEEE Spring Seminar on Electronics Technology, 2010, 33: 320-325.

[8] 刘强. 一种新型结构开关磁阻电机电磁场的有限元分析及起动性能分析[D]. 南京: 江苏大学，2005.

[9] EGGERS D, STEENTJES S, HAMEYER K. Advanced iron-loss estimation for nonlinear material behavior[J]. IEEE Transactions on Magnetics,2012,48 (11) :3021-3024.

[10] SEO, Jangho, CHUNG Taekyung, LEE Cheolgyun, et al. Harmonic iron loss analysis of electrical machines for high speed operation considering driving condition[J]. IEEE Transactions on Magnetics, 2009, 45(10): 4656-4659.

[11] 汤蕴璆，梁艳萍． 电机电磁场的分析与计算[M]. 北京: 机械工业出版社，2010: 169-203．

[12] 林鹤云，周鹦，黄健中.开关磁阻电机磁场有限元分析与铁耗计算[J]. 电工技术学报，1996,11(1):25-29.

[13] 杨丽，刘闯，严加根.开关磁阻电机铁损的双频法有限元计算研究[J].中国电机工程学报, 2006, 26(12) :117-121.

[14] BERTOTTI G.General properties of power losses in soft ferromagnetic material[J].IEEE Transactions on Magnetics，1998，24(1):621-630.

[15] DIAZ G, ARBOLEYA P, GONZALEZ-MORAN C.Revision of the hysteresis and excess loss computation method as a means of improving the rotational loss estimate in induction motors[J].IET on Electric Power Applications, 2007,1(1):75-81.

[16] GUO Y G, ZHU J G, ZHONG J J, et al.Measurement and modeling of rotational core losses of soft magnetic materials used in electrical machines: a review[J].IEEE Transactions on Magnetics, 2008,44(2):279-291.

[责任编辑：郝丽英]

Analysis of magnetic density and core loss of switched reluctance motor

GAO Xudong1，WANG Xifeng1,GAO Shanshan1，ZHANG Jiahang2

(1.College of Electrical and Information Engineering, Heilongjiang Institute of Technology, Harbin 150050, China;2.Heilongjiang Institute of Technology,Harbin 150050,China)

In this paper, a three-phase, 12/8 pole, 3kW switch reluctance motor(SRM) is selected as the prototype, based on the fundamental theory of electromagnetic field and the assumed conditions. The calculating model of electromagnetic field with field-road coupled, time-step finite element method is used to simulate and calculate under rated load working conditions. Both the distribution of gap flux density and harmonic content are analyzed in-depth, moreover, the core flux density of stator and rotor are calculated and analyzed. Based on this, with cores segmented, the core loss of each segment under rated load condition is calculated and some valuable conclusions can be drawn in the end.

SRM; time-step finite element method; gap flux density; core flux density; core loss

2017-02-26

哈尔滨市科技局创新人才研究专项基金项目(RC2015QN007008)

高旭东(1973-)，男，副教授，研究方向：电机智能控制;电力电子装置自动化.

10.19352/j.cnki.issn1671-4679.2017.04.007

TM352

A

1671-4679(2017)04-0027-06