基于扩展BP神经网络的一类非线性系统自适应控制设计

陈浩广，王银河

(广东工业大学 自动化学院，广州 510006)

基于扩展BP神经网络的一类非线性系统自适应控制设计

陈浩广*，王银河

(广东工业大学 自动化学院，广州 510006)

(*通信作者电子邮箱haoguang_chen@sina.cn)

针对单输入单输出非线性系统的不确定性问题，提出了一种新型的基于扩展反向传播(BP)神经网络的自适应控制方法。首先，采用离线数据来训练BP神经网络的权值向量;然后,通过在线调节伸缩因子和逼近精度估计值的更新律，从而来达到控制整个系统的目的。在控制器的设计过程中，利用李亚普诺夫稳定性分析原理，保证了闭环系统的所有状态一致终极有界(UUB)。相比传统的BP神经网络自适应控制，所提方法能有效地减少在线调节的参数数目、减轻计算负担。仿真结果表明，该方法能够使闭环系统的所有状态都趋于零，即系统达到稳定状态。

非线性系统；自适应控制；反向传播神经网络；一致终极有界；稳定性

0 引言

近年来，神经网络自适应控制已成为控制理论与工程应用领域中的一个研究热点，其研究成果为解决非线性不确定系统控制设计问题提供了重要方法[1-6]。这些成果的共同特点是：基于神经网络的万能逼近性能，利用神经网络逼近非线性系统中的未知不确定函数，然后采用自适应控制技术设计系统的控制器。在控制器的设计过程中，反向传播(Back Propagation, BP)神经网络因其强大的逼近性能、并行处理能力和强的鲁棒特性而被广泛采用。如文献[7]利用BP神经网络对被控对象进行在线辨识和控制，并结合常规的比例积分微分(Proportion Integration Differentiation, PID)控制器，提出了一种基于BP神经网络的自适应PID控制器。文献[8] 采用BP神经网络来逼近非线性离散系统中的未知动态项，通过结合一个死区算法来更新网络中的权值向量，保证了整个控制系统的稳定性和收敛性。文献[9]针对一类带有未知动态项或者噪声干扰项的仿射非线性系统，利用BP神经网络的万能逼近性能，提出了一种新型的控制律，并应用到气动伺服系统的位置跟踪控制，取得了良好的控制效果。虽然上述文献在自适应控制方面取得了不少突破，但它们仍旧没办法解决BP神经网络收敛速度慢的问题[10]，特别是当神经元的数目较多时，在线调节的自适应参数数目将大量增加，这样容易导致学习时间过长，使得控制效果不佳。另外，BP神经网络是一种局部寻优方法，权值是沿着局部改善的方向逐渐调整的。当它要解决一个全局的复杂非线性自适应控制问题时，很容易陷入局部极小值[11]，从而导致控制的失败。

为解决以上问题，不少学者针对BP神经网络自适应控制作了很多研究。文献[12]利用BP神经网络的误差反向传播机制，解决了控制器中的权值修正问题，使得该控制器具有良好的控制效果。文献[13]结合粒子群优化算法和BP神经网络的万能逼近特性，提出了一种新型的自适应控制方法。该方法不仅可以提高全局搜索能力，而且能够加快收敛。文献[14]提出了一种混合训练算法，其中输入层和隐层的权值训练采用的是自组织学习算法，隐层和输出层的权值训练采用的是梯度下降法，这种混合算法能够起到减少网络训练时间的作用。尽管以上方法在一定程度上减少自适应控制过程中参数的在线调节时间，但目前仍旧没有给出一种统一的、有规律可循的方法来解决这个问题。因此，本文提出了一种具有普遍性，能够适合任何一种神经网络类型(本文以BP神经网络为例)的解决方法。该方法在神经网络的输入输出端加载伸缩器和饱和器，先利用离线数据来训练神经网络的权值向量，再通过调节在线的自适应参数，最后实现了控制整个系统的目的。伸缩器和饱和器的加入，使得该方法在控制器的设计过程中，只需要调节伸缩因子和神经网络的逼近精度估计值，这样可以有效地减少在线的调节参数、减轻计算负担，并且能够保证整个闭环系统的所有状态一致终极有界。

1 预备知识与问题描述

定义3 在一个BP神经网络的输入端加载一个伸缩器和一个饱和器，并在其输出端加载一个伸缩器，结构如图1所示，称之为k阶扩展的BP神经网络系统(k-order extended BP neural network system)，记为ENS(N,k)。

图1 扩展的BP神经网络结构

图1中，扩展的BP神经网络ENS(N,k)的输出为：

(1)

当‖z/ξ‖≤ϖ时，有:

(2)

BP神经网络的输出为：

(3)

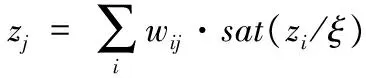
引理1 考虑在Rn上连续的k次齐次函数γ(z)，也即对于任意正实数λ满足γ(λz)=λkγ(z)。如果存在一个BP神经网络N和正实数M，在紧致域z∈{z|‖z‖≤ϖ}上满足:

(4)

那么扩展的BP神经网络ENS(N,k)的输出满足：

(5)

证明 由齐次函数的定义有γ(z)-ξkγ(z/ξ)=0，因此当z∈{z|‖z‖≤|ξ|ϖ}时，以下不等式成立：

|γ(z)-ξkN(z/ξ)|=|γ(z)-ξkγ(z/ξ)+ξk[γ(z/ξ)-N(z/ξ)]|= |ξ|k|γ(z/ξ)-N(z/ξ)|≤|ξ|kM

(6)

2 系统描述与假定

考虑如下非线性系统：

(7)

假定1 矩阵(A,B)是可控的，因此存在1×n阶矩阵K使A+BK是Hurwitz矩阵，并且对于任意给定的正定矩阵Q，下列Lyapunov方程有唯一正定矩阵解P：

(A+BK)TP+P(A+BK)=-Q

(8)

(9)

由引理1和假定3，可以得到下面不等式：

j=0,1,…,s

(10)

3 神经网络自适应控制设计

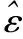
(11)

(12)

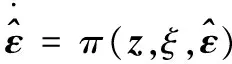
(13)

(14)

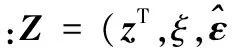
情况a 当‖z‖>|ξ|ϖ时，利用神经网络Nj逼近连续齐次函数Δj，同时采用如下的控制输入和更新律：

u=0

(15)

(16)

(17)

其中：λ和β是可调的正常数。

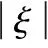
(18)

根据文献[15]和式(18)，可以知道闭环系统的状态能在有限的时间内到达曲面s=0，即{Z|s=0}⊆D。

引理2得证。

情况b 当‖z‖≤|ξ|ϖ时，设计控制器：

u=u1+u2

(19)

(20)

(21)

伸缩因子和逼近精度估计值的更新律分别是：

(22)

(23)

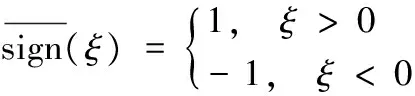
(24)

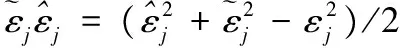
(25)

由式(25)得到不等式：

(26)

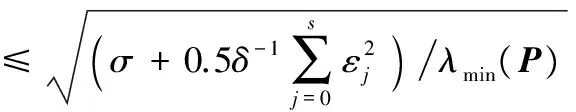
(27)

(28)

(29)

引理3得证。

结合以上两种情况，可以得出下面定理。

整个神经网络自适应控制的设计流程如图2所示。

图2 神经网络自适应控制设计流程

4 算例仿真和分析

考虑如下二阶系统：

(30)

根据假定2～3，需要离线数据训练三个BP神经网络N0、N1、N2来逼近未知的连续齐次函数Δ0=-Kz、Δ1=h1(z)、Δ2=h2(z)，其中K=(-3,-4)。在训练过程中，采用的算法是梯度下降法。神经网络的层数是3层，隐层的神经元个数为6，网络结构是：1—6—1。训练完成后，将可以得到相应的网络权值，并保持这些权值不变。

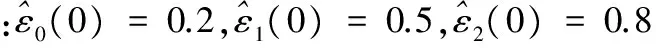
图3 不同参数的时间相应曲线

5 结语

本文利用李亚普诺夫稳定性分析原理，设计了一种基于扩展BP神经网络的自适应稳定控制器。该控制器结合了离线训练与在线调节，很好地解决了传统BP神经网络收敛速度慢的缺点，并通过在线调节伸缩因子和逼近精度估计值的更新律，来保证闭环系统的所有状态达到一致终极有界。但是，该控制器在设计过程中，需要假定被控系统的未知函数能分解成连续的齐次函数。因此，其应用范围受到了一定的限制。在今后的研究中，可以考虑是否通过引进Lipschitz条件，来消除这个局限。

)

[1] 吴玉香,王聪.不确定机器人的自适应神经网络控制与学习[J].控制理论与应用,2013,30(8):990-997.(WUYX,WANGC.Adaptiveneuralnetworkcontrolandlearningforuncertainrobot[J].ControlTheoryandApplications, 2013, 30(8): 990-997.)

[2]ZUOY,WANGYN,LIUXZ.NeuralnetworkrobustH∞-trackingcontrolstrategyforrobotmanipulators[J].AppliedMathematicalModeling, 2010, 34(7):1823-1838.

[3]CHANGYC,YENHM.Robusttrackingcontrolforaclassofuncertainelectricallydrivenrobots[J].IETControlTheory&Applications, 2009, 3(5): 519-532.

[4]CHENB,ZHANGHG,LINC.Observer-basedadaptiveneuralnetworkcontrolfornonlinearsystemsinnonstrict-feedbackform[J].IEEETransactionsonNeuralNetworksandLearningSystems, 2016, 27(1): 89-98.

[5]SAHOOA,XUH,JAGANNATHANS.Adaptiveneuralnetwork-basedevent-triggeredcontrolofsingle-inputsingle-outputnonlineardiscrete-timesystems[J].IEEETransactionsonNeuralNetworksandLearningSystems, 2016, 27(1): 151-164.

[6]GAOSG,DONGHR,NINGB,etal.NeuraladaptivecontrolforuncertainMIMOsystemswithconstrainedinputviainterceptedadaptationandsinglelearningparameterapproach[J].NonlinearDynamics, 2015, 82(3): 1109-1126.

[7] 谭永红.基于BP神经网络的自适应控制[J].控制理论与应用,1994,11(1):84-88.(TANYH.AdaptivecontrolbasedonBPneuralnetwork[J].ControlTheoryandApplications, 1994, 11(1): 84-88.)

[8]LIXL,LIUDX,LIJY,etal.Robustadaptivecontrolfornonlineardiscrete-timesystemsbyusingmultiplemodels[J].MathematicalProblemsinEngineering, 2013(8): 1-10.

[9]LUL,LIUFG,SHIWX.Neural-networkadaptivecontrollerfornonlinearsystemsanditsapplicationinpneumaticservosystems[J].JournalofControlTheoryandApplications, 2008, 6(1): 97-103.

[10] 张昭昭,乔俊飞,杨刚.一种功能分区的BP神经网络结构设计方法[J].控制与决策,2011,26(11):1659-1664.(ZHANGZZ,QIAOJF,YANGG.Structuremodeloffunction-dividingdesignforBPneuralnetwork[J].ControlandDecision, 2011, 26(11): 1659-1664.)

[11] 冯立颖.改进的BP神经网络算法及其应用[J].计算机仿真,2010,27(12):172-175.(FENGLY.OptimizedBPneuralnetworksalgorithmanditsapplication[J].ComputerSimulation, 2010, 27(12): 172-175.)

[12] 沈瑛,张翠芳.基于BP神经网络的模型参考自适应控制[J].西南交通大学学报,2001,36(5):553-556.(SHENY,ZHANGCF.ModelreferenceadaptivecontrolbasedonBPneuralnetworks[J].JournalofSouthwestJiaotongUniversity, 2001, 36(5): 553-556.)

[13]ZHANGJR,ZHANGJ,LOKTM,etal.Ahybridparticleswarmoptimization-back-propagationalgorithmforfeedforwardneuralnetworktraining[J].AppliedMathematicsandComputation, 2007, 185(2): 1026-1037.

[14]NASRMB,CHTOUROUM.Neuralnetworkcontrolofnonlineardynamicsystemsusinghybridalgorithm[J].AppliedSoftComputing, 2014, 24: 423-431.

[15]SLOTINEJE,LIW.AppliedNonlinearControl[M].UpperSaddleRiver,NJ:Prentice-Hall, 1991: 251-253.

[16]WANGM,WANGC,LIUXP.Dynamiclearningfromadaptiveneuralcontrolwithpredefinedperformanceforaclassofnonlinearsystems[J].InformationSciences, 2014, 279: 874-888.

ThisworkispartiallysupportedbytheNationalNaturalScienceFoundationofChina(61273219, 61673120),theSpecializedResearchFundfortheDoctoralProgramofHigherEducationofChina(20134420110003).

CHEN Haoguang, born in 1986, Ph. D. candidate. His research interests include neural network, fuzzy control.

WANG Yinhe, born in 1962, Ph. D., professor. His research interests include complex network, nonlinear control.

Adaptive control design for a class of nonlinear systems based on extended BP neural network

CHEN Haoguang*, WANG Yinhe

(SchoolofAutomation,GuangdongUniversityofTechnology,GuangzhouGuangdong510006,China)

Aiming at the uncertainty of Single-Input-Single-Output (SISO) nonlinear systems, a novel adaptive control design based on extended Back Propagation (BP) neural network was proposed. Firstly, the weight vectors of BP neural network were trained via the offline data. Then, the scaling factor and estimation parameter of approximate accuracy were adjusted online to control the whole system by update law. In the design process of controller, with the Lyapunov stability analysis, the adaptive control scheme was proposed to guarantee that all the states of the closed-loop system were Uniformly Ultimately Bounded (UUB). Compared with the traditional adaptive control method of BP neural network, the proposed method can effectively decrease the parameter number of online adjustment and reduce the burden of computation. The simulation results show that the proposed method can make all the states of the closed-loop system tend to be zero, which means the system reaches the steady state.

nonlinear system; adaptive control; Back Propagation (BP) neural network; uniformly ultimately bounded; stability

2016- 12- 05;

2017- 03- 02。

国家自然科学基金资助项目(61273219,61673120); 教育部高等学校博士学科点专项科研基金资助项目(20134420110003)。

陈浩广(1986—)，男，广东汕头人，博士研究生，主要研究方向：神经网络、模糊控制； 王银河(1962—)，男，内蒙古包头人，教授，博士，主要研究方向：复杂网络、非线性控制。

1001- 9081(2017)06- 1670- 04

10.11772/j.issn.1001- 9081.2017.06.1670

TP183; TP273

A