西南某水电站滑坡稳定性及其失稳影响研究

2017-09-03邓卫东

资源环境与工程 2017年4期

关键词：滑体前缘滑动

邓卫东

(中国电建集团成都勘测设计研究院有限公司,四川成都 610072)

西南某水电站滑坡稳定性及其失稳影响研究

邓卫东

(中国电建集团成都勘测设计研究院有限公司,四川成都 610072)

麻日滑坡前缘发育3个次级滑体。根据河谷斜坡变形演化机制分析，利用数值模拟及刚体极限平衡计算分析其稳定性，研究结果表明，2#次级滑体发生失稳的可能性较大，但失稳方量小于最小堵江方量，堵江可能性小；另外，对3个次级滑体分别进行涌浪分析和计算，推测涌浪到达坝址的最大涌浪高度。

滑坡;稳定性;计算;影响程度;水电站

设计中的西南某水电站位于雅砻江干流上,挡水坝最大坝高118 m,利用落差88 m,总装机容量400 MW,为大(2)型工程。

麻日滑坡位于水电站坝址上游5.8 km雅砻江右岸。通过现场查勘,滑坡目前前缘局部有滑塌现象。水库蓄水后,滑坡前缘70 m将处于水库正常水位下,滑坡失稳对电站大坝危害极大,对坝址的选择及坝型的研究具有重要的影响;水库区为藏文化核心区,水库蓄水后,滑坡失稳后产生涌浪将对库区寺庙、场镇、通村公路等处形成威胁。因此,通过河谷斜坡变形演化机制、数值模拟及滑坡稳定性刚体极限平衡,查明滑坡的整体及次级滑体的稳定性,并进行滑坡失稳涌浪计算分析[1],从而准确评价其稳定性及影响程度,对防治具有十分重要的意义。

1 滑坡区基本地质条件

麻日滑坡位于坝址上游约5.8 km,雅砻江右岸(如图1),河流流向近S,河谷较为宽阔,河面宽约46 m,河水位2 965 m。

滑坡处岸坡岩层产状走向北东10°,倾向南西,倾角70°～80°,为陡倾逆向坡。岩性为三叠系上统雅江组中薄层状砂岩与薄层状板岩互层。

麻日滑坡在平面圈椅状地貌,顺河宽约676 m,横河长约900 m,滑坡前、后缘高程分别为2 965 m和3 670 m,相对高差为705 m,滑坡总面积约54万m2,滑体厚100～140 m,方量约3 600万m3。

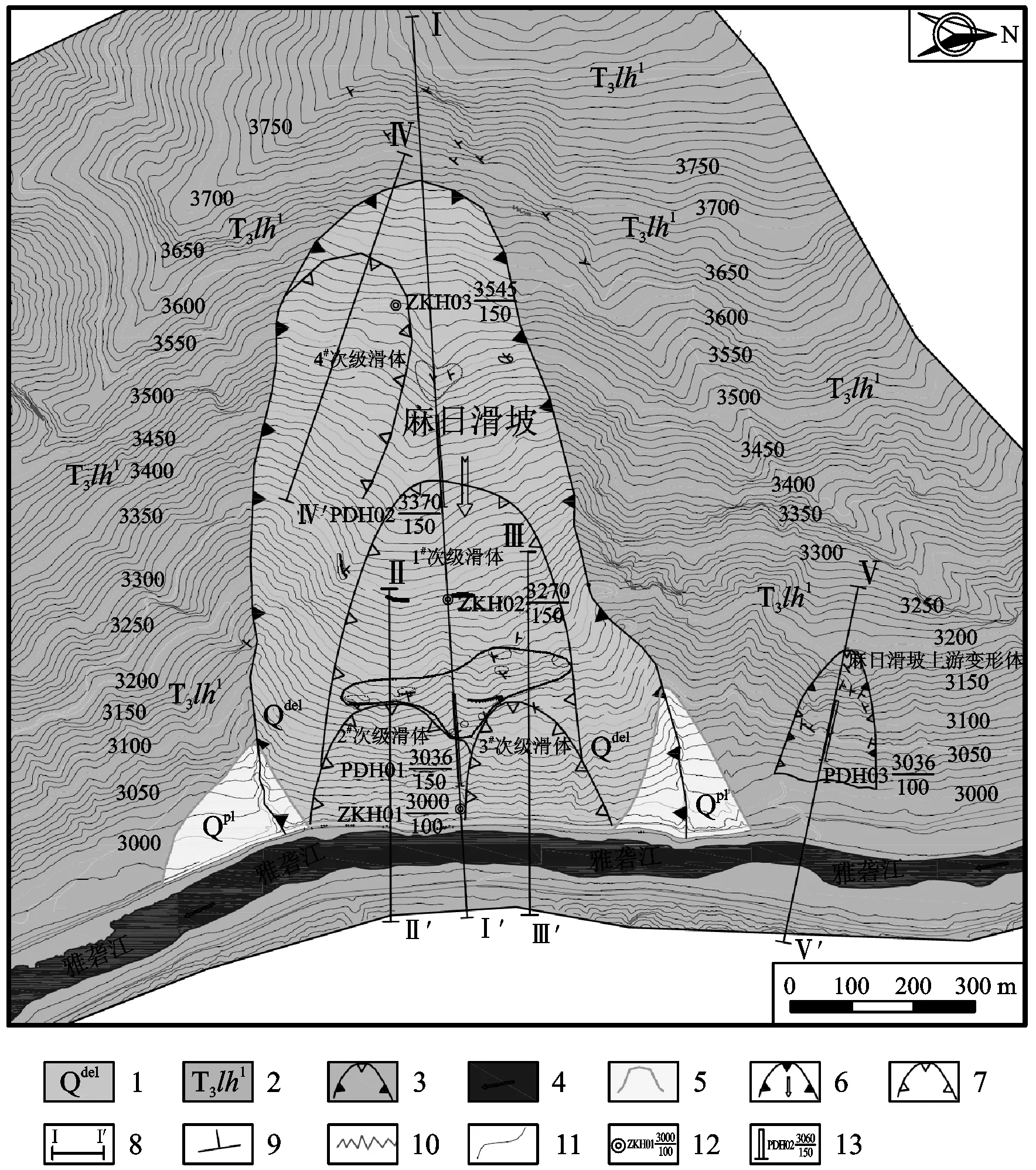
图1 麻日滑坡工程地质平面图Fig.1 The plan of engineering geology of Mari landslide1.滑坡堆积体;2.两河口组下段变质砂岩夹板岩;3.变形体；4.雅砻江;5.泥石流堆积区;6.滑坡边界及主滑方向;7.次级滑体边界;8.剖面线;9.岩层产状;10.裂缝;11.地质界线;12.钻孔孔号平硐编号

滑坡呈明显的圈椅状滑坡地貌。后缘边界为基岩陡坎,两侧以冲沟为界,其中,后缘基岩陡坎高约30 m,为变质砂岩夹板岩(板岩较破碎,层厚约30 cm),滑体见明显的下错台阶,呈阶梯状。滑坡体前缘临河坡度约为40°～45°,中部坡度约为30°～38°,后缘坡度约为33°～37°。

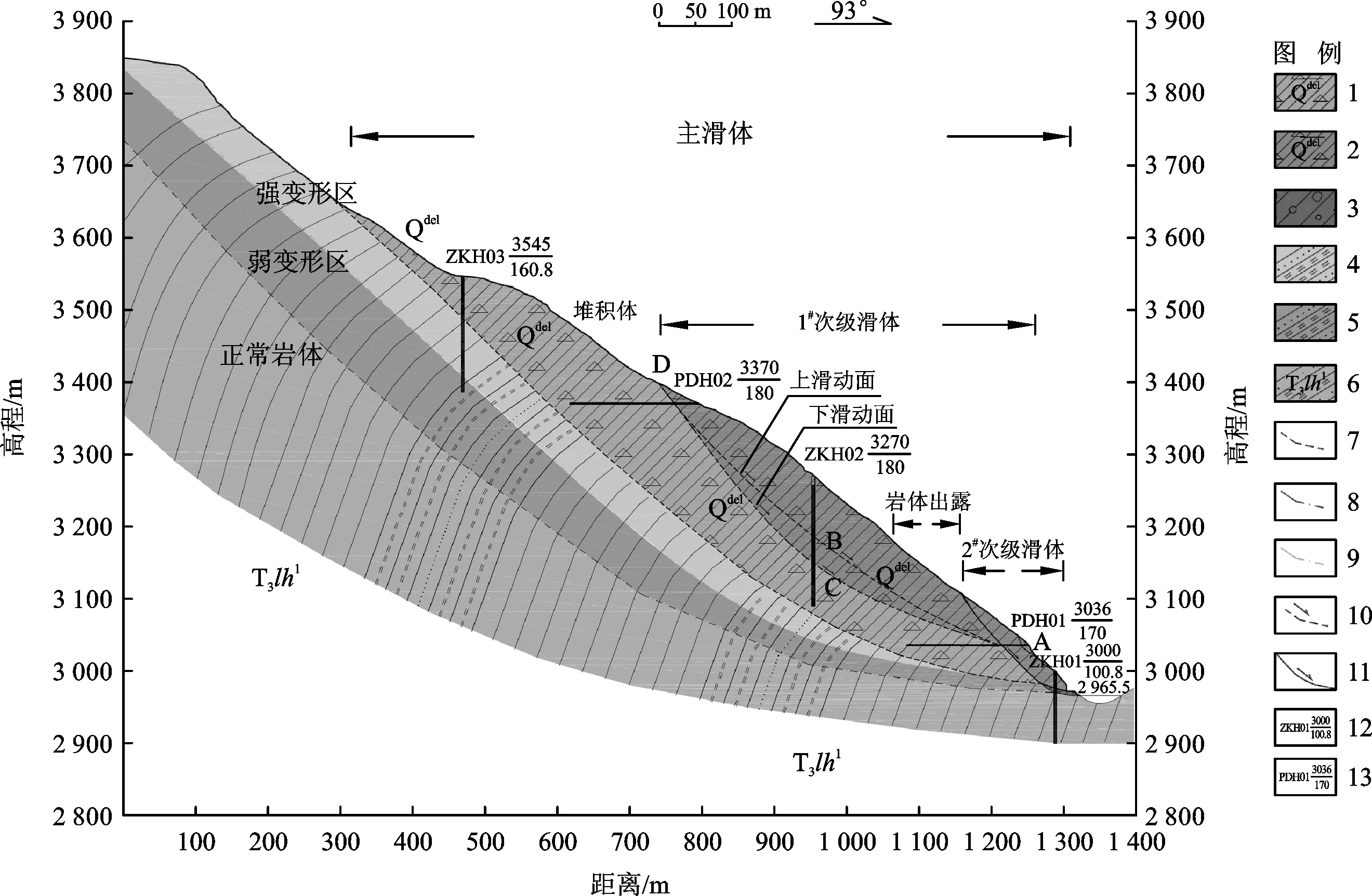
图3 麻日滑坡Ⅰ-Ⅰ剖面图Fig.3 Ⅰ-Ⅰ profile of the Mari landslide1.滑坡堆积物含碎石粉质粘土;2.次级滑坡堆积物含碎石粉质粘土;3.卵石夹粉质粘土;4.强变形区;5.弱变形区;6.三叠系上统两河口组下段变质砂岩夹板岩;7.主滑坡滑动面;8.弱变形区下界限;9.强变形区下界限;10.潜在滑动面;11.堆积层滑动面;12.钻孔孔号平硐编号

滑坡体内发育有四个次级滑体,从上游至下游,依次为:1#、2#、3#和4#次级滑体,次级滑体体积分别约为558.2万m3、50.7万m3、45.3万m3、105.2万m3。4个次级滑体中,除4#次级滑体后缘未有明显拉张裂缝外,1#、2#、3#次级滑体后缘及侧缘均分布有明显的下错台坎,滑体内多条拉张裂缝。滑体物质成分主要为块碎砾石土及未完全解体砂板岩。钻孔岩芯、平洞内见滑带,其物质组成为粘土夹少量碎石,次级滑体滑带为灰白色碎块石土,成分为炭质板岩。

2 滑动破坏模式

根据地表地质测绘及平洞、钻孔勘探资料分析,滑坡区域内岩层倾倒变形严重,岩层正常产状为N10°E/NW∠70°～80°,倾倒岩层产状为N10°～15°E/NW∠5°～35°,因此,推测滑坡滑动破坏模式为倾倒弯曲—拉裂型。

滑坡的滑动与岩层倾倒现象有密切的关系[2],根据岩层倾角与深度的关系可划分为强(<40°)、弱(40°～70°)、正常岩体(>70°)(如图2),推测滑床为强倾倒变形变质砂岩夹板岩,其岩层属缓倾坡内,倾角约为20°～30°(如图3)。

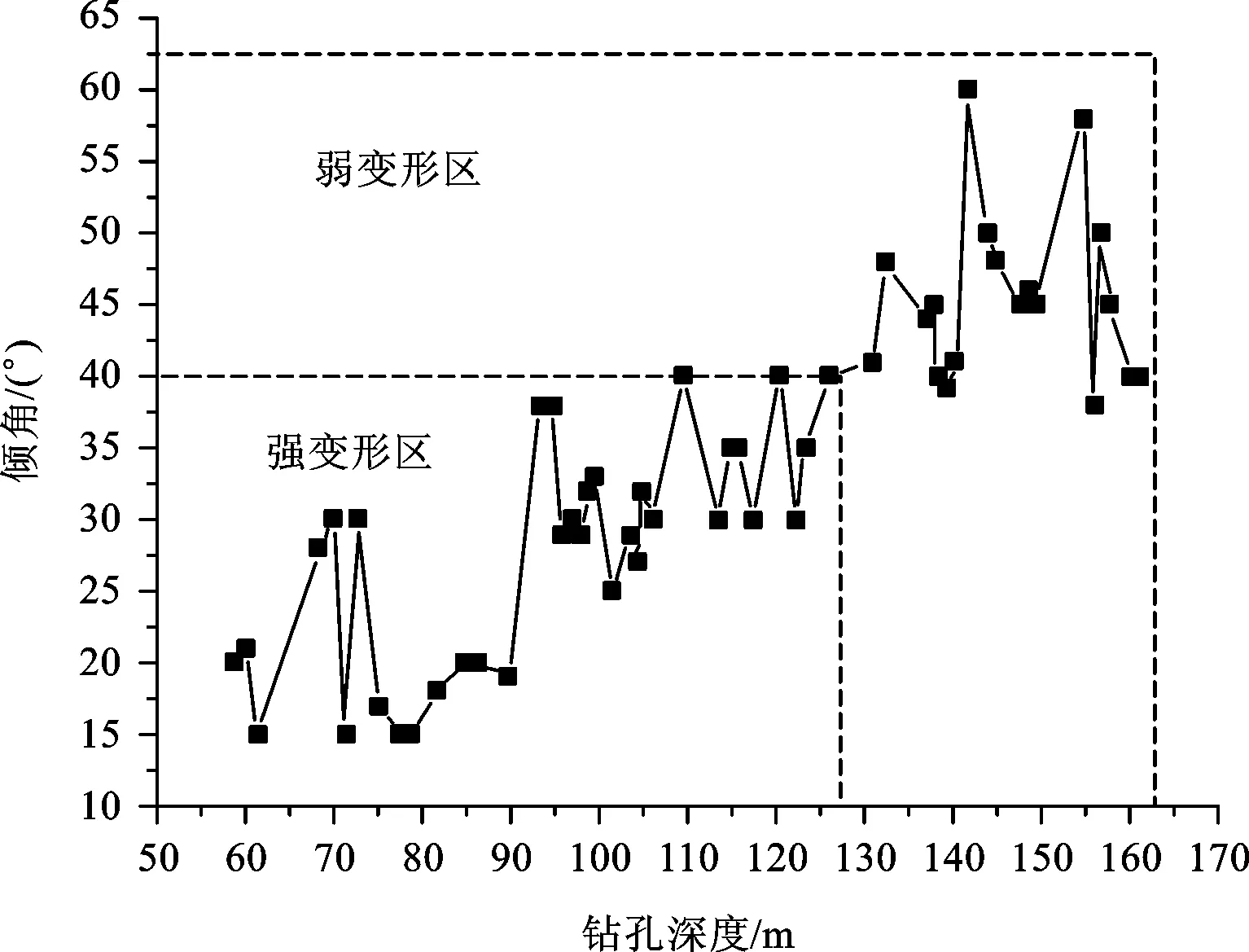
图2 典型钻孔ZKH03岩层倾角与深度的分布关系图Fig.2 The dip angles and depth distribution of typical borehole ZKH03

3 斜坡变形演化机制

工程区地貌特征为地势高、切割深、高差大。通过斜坡变形演化时空特征,分析该滑坡的变形演化机制,认为斜坡属于弯曲倾倒—拉裂型。其形成过程为边坡在河流下切及侵蚀作用下,发生弯曲—拉裂折断滑移破坏,滑坡失稳后受雅砻江河水冲刷切割,引发了多次解体和崩塌,最终演化成现有空间形态[3-7]。依据斜坡的演化过程可分为如下六个阶段:

(1) 临空面形成阶段(如图4)。斜坡处于雅砻江复式背斜的西翼,地层为三叠系上统两河口组下段变质砂岩夹板岩,该阶段随着地壳抬升和河流的下切侵蚀,斜坡前缘临空面开始形成。

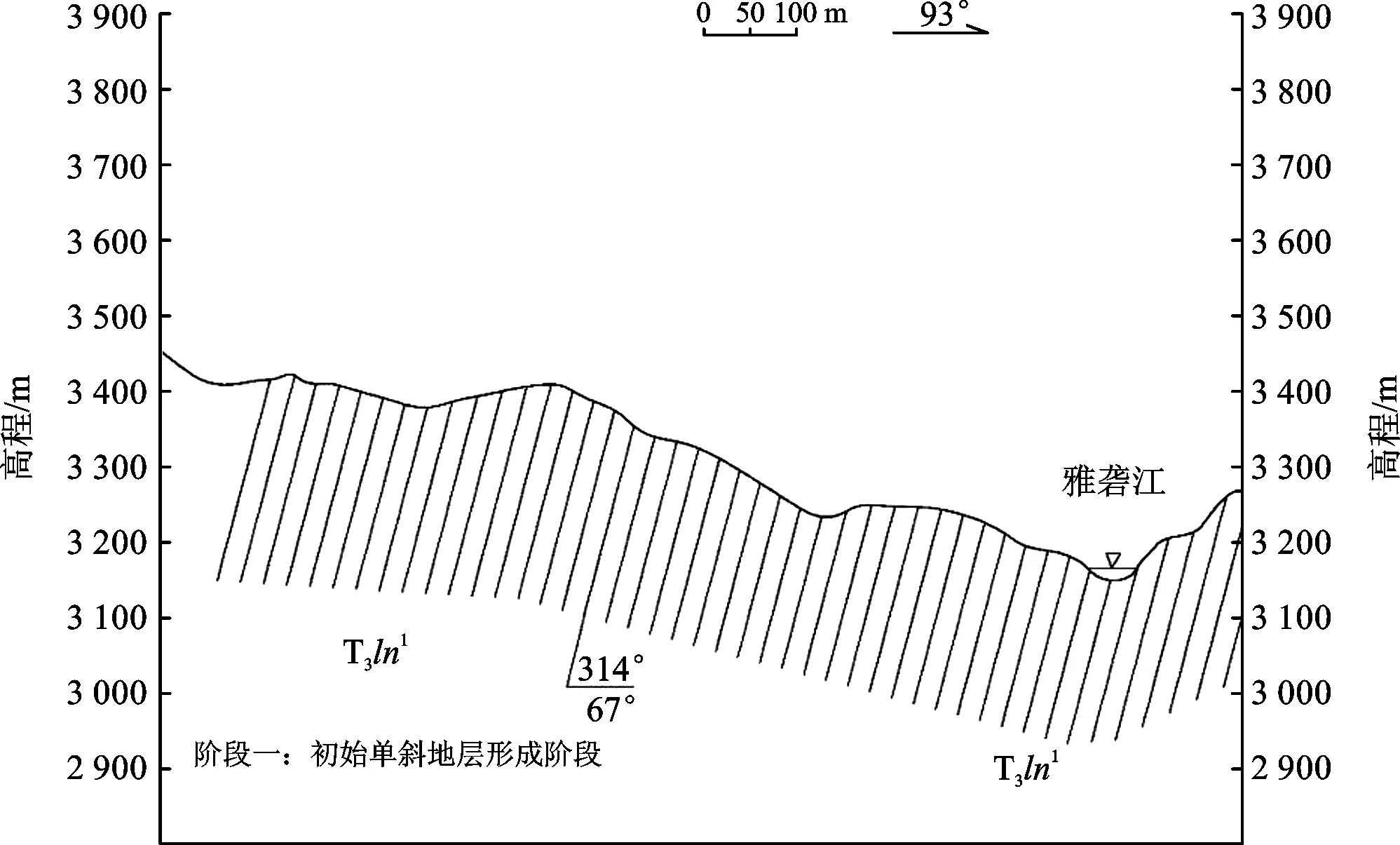
图4 斜坡变形演化阶段一示意图Fig.4 Diagram of the first stages of slope deformation

(2) 斜坡岩体在应力作用下沿结构面初始变形阶段(如图5)。河流下切形成的河谷地形,伴随卸荷作用,坡体后缘岩体应力为拉应力分布区,坡脚地带为剪应力集中区,因此,坡体中后部岩体因卸荷回弹,沿板理面拉裂、错动;坡体内陡倾结构面发生拉裂、错动,表面出现微小台阶或在坡肩形成拉裂缝;前缘近垂直于层面发育的一组节理面。在斜坡应力作用下,发生剪切蠕滑,为岩体的进一步变形奠定了基础。

(3) 岩层弯曲变形、前缘剪切蠕变、后缘拉裂缝变形阶段(如图6)。地壳抬升运动作用下,雅砻江河谷演化至T2级阶地,伴随河流下切侵蚀作用,形成原始坡表地形及地质构造。尤其是在河谷凹岸强烈侧蚀作用下,斜坡底部被冲刷侵蚀,形成前缘临空面地形。边坡在重力场作用下,岩体向河谷临空方向作“悬臂梁”倾倒弯曲变形。

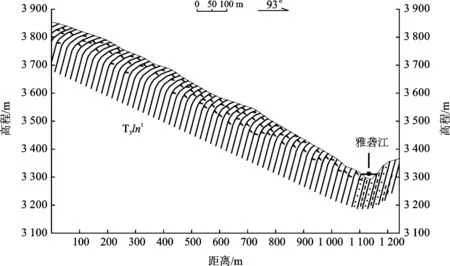
图5 斜坡变形演化阶段二示意图Fig.5 Diagram of the second stages of slope deformation

图6 斜坡变形演化阶段三示意图Fig.6 Diagram of the third stages of slope deformation

(4) 1#潜在滑面形成阶段(如图7)。随着层状岩体长期弯曲倾倒作用,强变形区内岩体破碎程度进一步发育,变形加剧并向坡内发展,顺坡拉裂缝相互贯通,形成统一的滑动面。在地震或暴雨等条件下,诱发弯折破坏整体性失稳滑动,滑坡体入江堵塞雅砻江,河流进一步下切,前缘形成临空面,强变形区表层岩体弯曲倾倒变形加剧,并沿着拉裂缝及破裂面逐步贯通,形成1#潜在滑动面。

(5) 2#潜在滑移面形成阶段(如图8)。河流下切,前缘滑坡堆积物受河水冲刷作用形成临空面,中部强变形岩体失去底部坡脚支撑,弯曲倾倒变形加剧,中上部浅表岩体崩塌脱落,在坡脚处堆积,形成崩坡积物。河流下切至T1阶地高程,前缘崩坡积物受河水冲刷作用形成临空面,崩坡积物失去坡脚反力,失稳形成2#次级滑体。

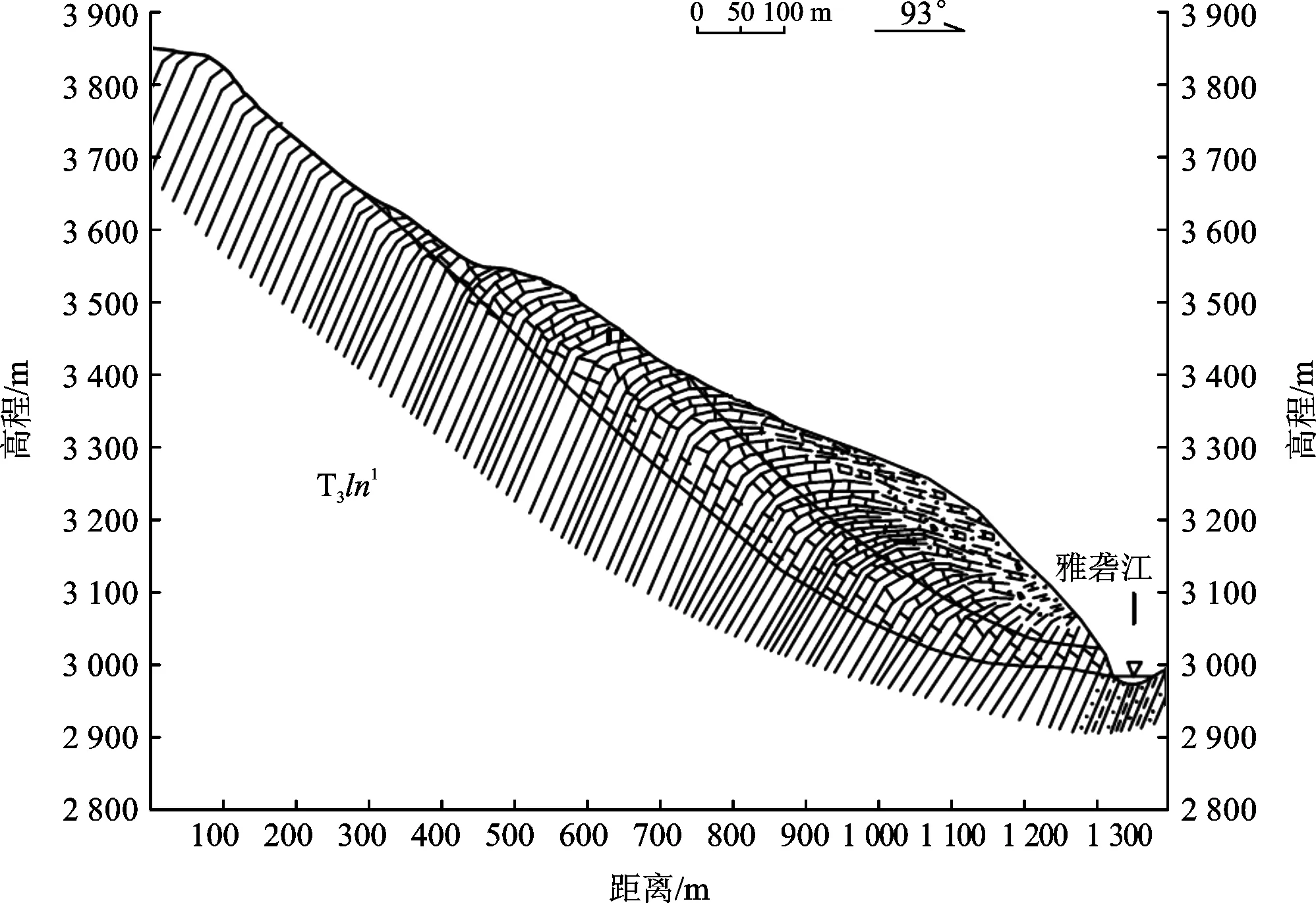
图7 斜坡变形演化阶段四示意图Fig.7 Diagram of the forth stages of slope deformation

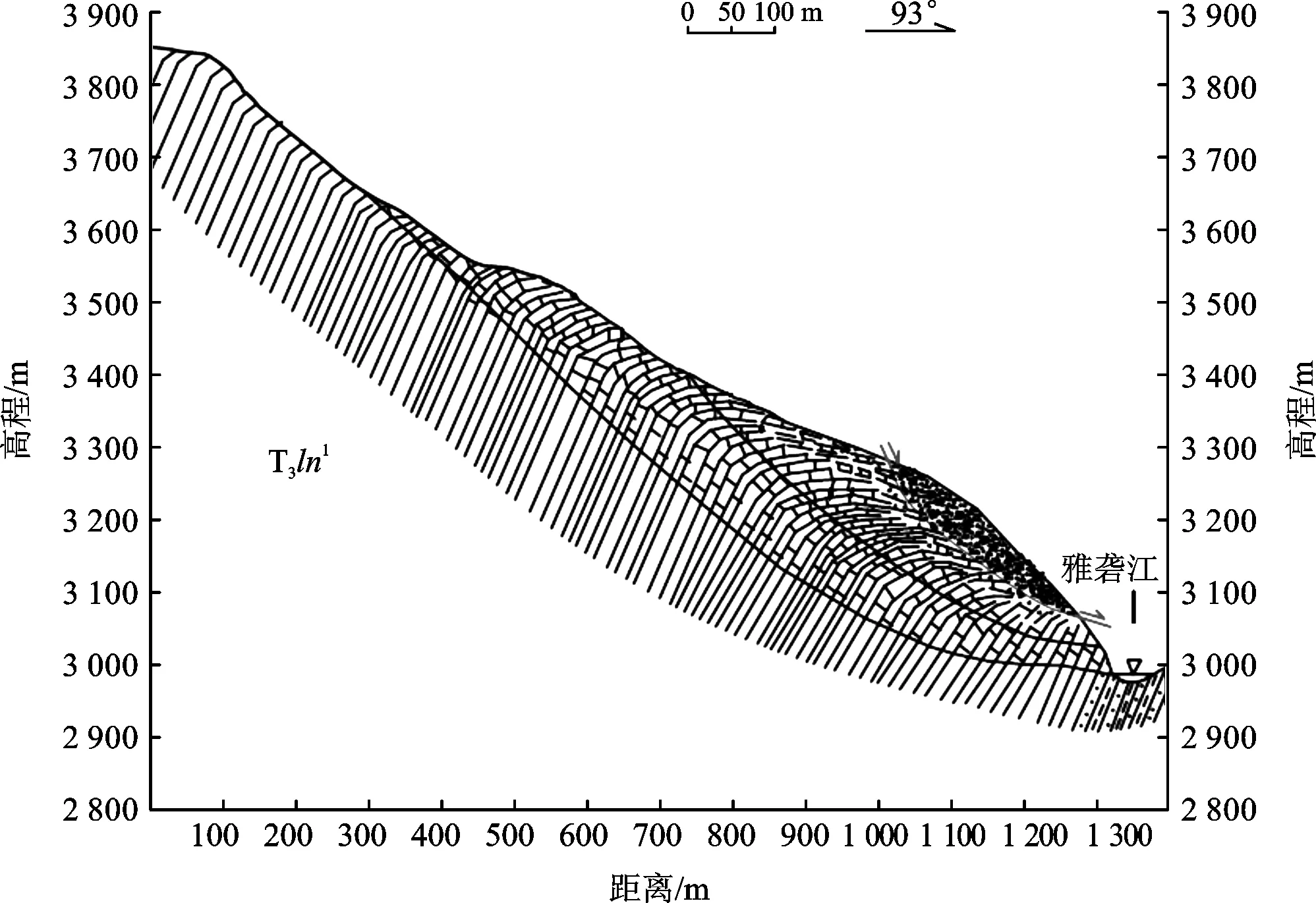
图8 斜坡变形演化阶段五示意图Fig.8 Diagram of the fifth stages of slope deformation

(6) 人类工程影响阶段(如图9)。伴随着河流下切侵蚀和冲刷作用,以及人类工程活动造成的坡脚公路开挖,2#次级滑体浅表崩坡积物垮塌,呈现出现有的空间特征。

从上述过程可看出滑坡历史上经历多次解体滑动,其中滑坡体内存在3个规模相对较大的潜在不稳定体,从深部向浅表依次为主滑坡体和1#次级滑体、2#次级滑体、3#次级滑体,滑坡复活解体模式以后退式解体为主。

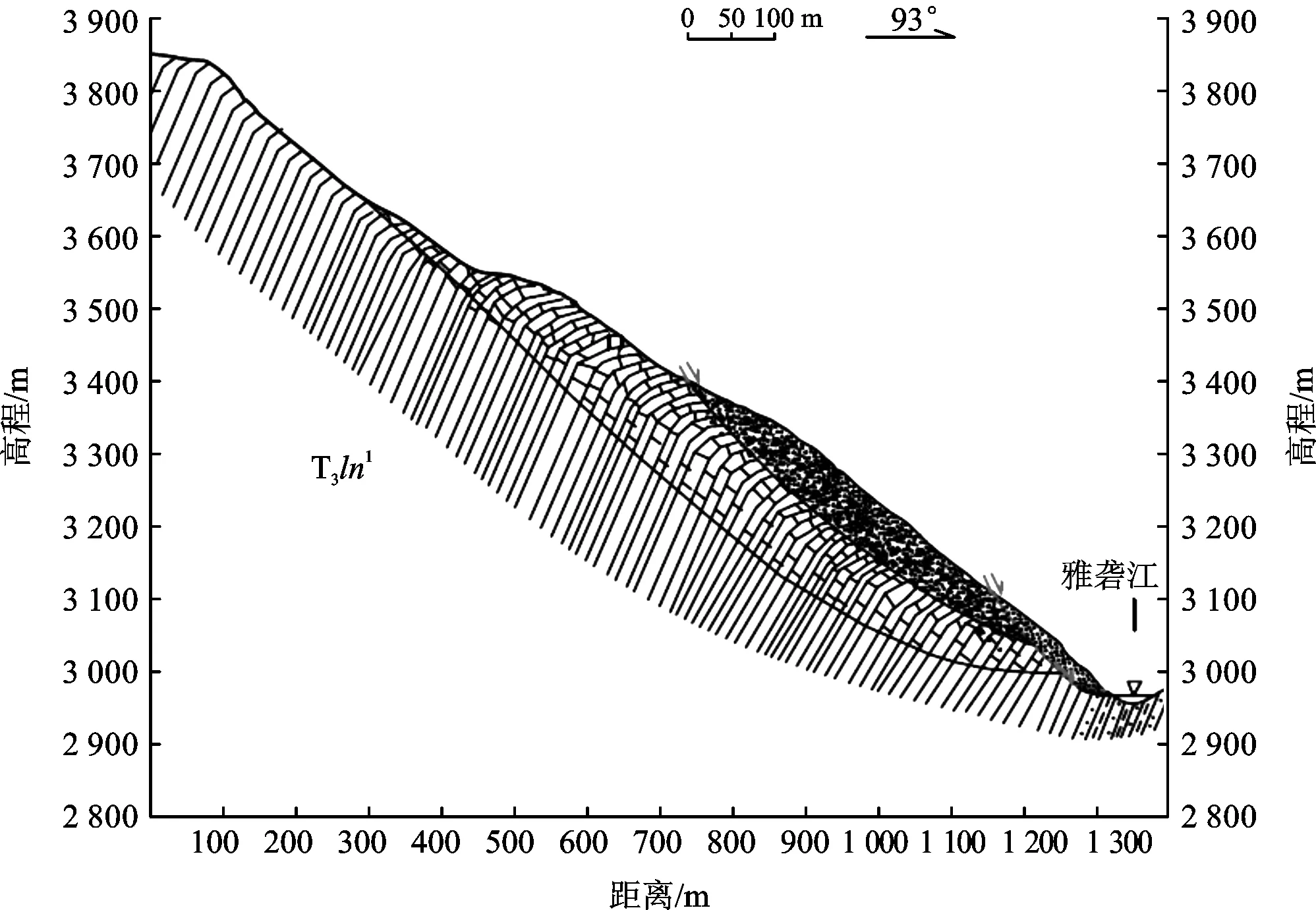
图9 斜坡变形演化阶段六示意图Fig.9 Diagram of the sixth stages of slope deformation

4 数值模拟

采用有限元(Geo-studio)渗流分析模块(SEEP)联合有限差分来计算麻日滑坡在库水位波动以及降雨作用下,其稳定性和变形发展过程。具体计算方法如下:采用饱和—非饱和渗流理论计算麻日滑坡地下水渗流场的动态变化过程。二维饱和—非饱和渗流微分方程可由Darcy定律和质量守恒定律联合推导得出,当采用水头h作为控制方程的因变量时,渗流微分方程可以写成如下形式:

(1)

式中:kx,ky分别为水平和垂直方向的饱和渗透系数;h为总水头;Q为施加的边界流量;mw为比水容积;γw为水的重度。接着将渗流场计算结果导入到有限差分计算软件(FLAC3D)中,以此为基础计算麻日滑坡的变形发展过程。

4.1 二维渗流分析

通过麻日滑坡滑体、滑带和滑床等滑坡结构体的地质信息构建滑坡地质模型(如图10),在进行渗流场计算时,左、右两侧边界设为不透水边界,坡面按照水位变化设为动水头边界。采用SEEP渗流分析模块,以1 d为时步间隔,获取麻日滑坡在库水位调蓄过程中的地下水渗流场。

分析各种工况发现,麻日滑坡的2#次级滑体前缘受库水位涨落的影响相对较大,尤其是在库水位下降的过程中,由于前缘浸润线下降的滞后,将在滑坡体前缘产生较大的超静孔隙水压力,对浅层滑坡的稳定性较为不利。且在降雨作用下,麻日滑坡的地下水渗流场有较为明显的变化,这对2#次级滑体的稳定性有一定影响。

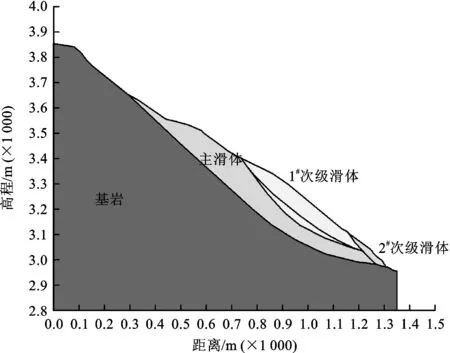
图10 麻日滑坡渗流模型剖面图Fig.10 The seepage model profile of Mari landslide

4.2 数值模拟分析

采用FLAC3D来计算麻日滑坡在库水位波动以及在降雨作用下,计算其稳定性及变形的发展过程,典型剖面Ⅰ-Ⅰ模型如图11所示,模型由25 830个节点,12 691个单元组成。

图11 Ⅰ-Ⅰ剖面有限差分数值计算模型Fig.11 The finite difference numerical model of Ⅰ-Ⅰ profile

1#次级滑体:该次级滑体整体位移较小。蓄水前,在天然工况、暴雨工况和暴雨叠加地震工况中变形均较小,滑体处于稳定状态;蓄水后,滑体位移量增加不明显,天然状态增大了9 cm,暴雨状态增大了30 cm,地震状态增大了40 cm。表明蓄水对1#次级滑体稳定性有一定影响,但在蓄水后仍将处于稳定状态,滑动破坏的可能性较小。

2#次级滑体:该次级滑体整体位移较大。蓄水前,在暴雨状态时前缘滑体最大位移量达到34 cm,滑体处于欠稳定状态;在暴雨叠加地震工况下,位移达到了2.2 m,模型计算不收敛,滑体处于不稳定状态,存在发生滑动破坏的可能;蓄水后,滑体位移量增加明显,从天然状态时15 cm增至27.2 cm,且剪应变增量带贯通。说明蓄水对2#次级滑体稳定性有较大影响,滑体处于不稳定状态。在暴雨状态和地震状态时,位移量增大,且计算不收敛,滑体处于不稳定状态,存在发生滑动破坏的可能。

综合分析,在水库蓄水前,麻日滑坡1#和2#次级滑体,1#次级滑体稳定性相对较好,在各种工况下均处于基本稳定—稳定状态,仅在暴雨和地震叠加的极端工况下处于欠稳定状态。而2#次级滑体稳定性计算结果相对较低,仅在天然和暴雨工况下处于基本稳定—欠稳定状态,但在暴雨和地震叠加工况下,以及蓄水后的暴雨和地震工况下滑体处于不稳定状态。在水库蓄水后,结果表明蓄水对各个次级滑体均有一定影响,尤其是2#次级滑体,发生失稳的可能性较大。当2#次级滑体失稳破坏,会造成1#次级滑体前缘临空,从而会降低1#次级滑体整体稳定性。

5 滑坡稳定性刚体极限平衡

根据野外调查和地质勘探资料,运用加拿大GEO-SLOPE公司开发的Geo-Studio系列软件中的SLOPE模块对麻日滑坡进行稳定性刚体极限平衡分析。结合滑坡变形破坏特征及次级滑体发育情况,选取滑坡变形区内典型纵剖面建立其计算模型[8](如图12),采用指定滑面法,分别计算主滑体、1#、2#和3#次级滑体及强变形区的稳定性。滑坡稳定性计算结果见表1，其表明如下。

图12 麻日滑坡剖面计算模型Fig.12 The calculation model of the section of Mari landslide

(1) 水库蓄水前,麻日滑坡1#次级滑体稳定性较好,在天然工况下处于稳定状态,在暴雨或地震工况下稳定性有所下降,但仍处于基本稳定状态,而在暴雨和地震叠加的极端工况下处于欠稳定状态;2#、3#次级滑体稳定性较差,在天然工况下处于基本稳定状态,在暴雨或地震工况下处于临界的欠稳定状态,在暴雨和地震叠加的极端工况下处于不稳定状态;主滑体稳定性相对较好,在各工况下处于基本稳定—稳定状态;强变形区稳定性好,在各工况下处于稳定状态。

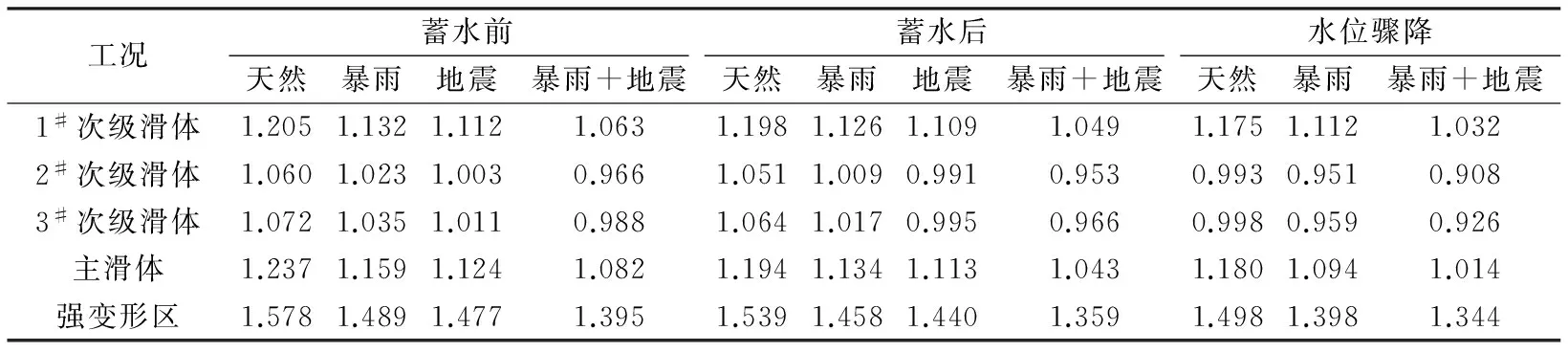
表1 滑坡稳定性计算结果一览表Table 1 The stability calculation results of landslide

(2) 水库蓄水后,由于滑面前缘剪出口处均处在水位以下,受库水位浸泡滑面处抗剪强度减小,从而导致抗滑力减小,各滑坡稳定性下降。

(3) 水位骤降条件下对于滑坡稳定性的不利影响较大,计算结果显示水位骤降时2#和3#次级滑体均处于不稳定状态,极易发生整体失稳。这是因为2#、3#约有一半方量的滑体处于水位以下,在水位下降时,坡体内产生的动水压力作用和水头差均指向坡外,增加了坡体的下滑力。

(4) 2#、3#滑体失稳后,1#次级滑体前缘临空,前缘抗滑力减小,在暴雨和地震工况下1#次级滑体都存在发生失稳的可能。

6 滑坡工程影响

根据刚体极限平衡法计算和数值模拟变形分析,2#和3#次级滑体在暴雨和地震叠加工况下处于不稳定状态。蓄水后,水位抬升约70 m,正常蓄水位下滑体约有1/2将会受到库水浸泡和冲刷,其稳定性将进一步降低。且如2#、3#次级滑体失稳,1#次级滑体也将在暴雨与地震工况下存在失稳的可能。因此,有必要对1#、2#、3#滑体进行堵江涌浪计算。

6.1 滑速计算

采用平均速度法来计算滑坡启动时的滑动速度。该方法假设滑体滑落于半无限水体中,且将滑体视为质点进行研究,按照牛顿第二定律及运动学基本原理推导出滑坡加速度及速度计算公式[9]。滑坡受力如图13,滑坡入水时速度公式:

(2)

式中:V为平均速度(m/s);L为滑坡体长度(m);H为滑坡水上部分重心—水面高度(m);α为滑面倾角(°);φ′为抗剪断摩擦角(°)。

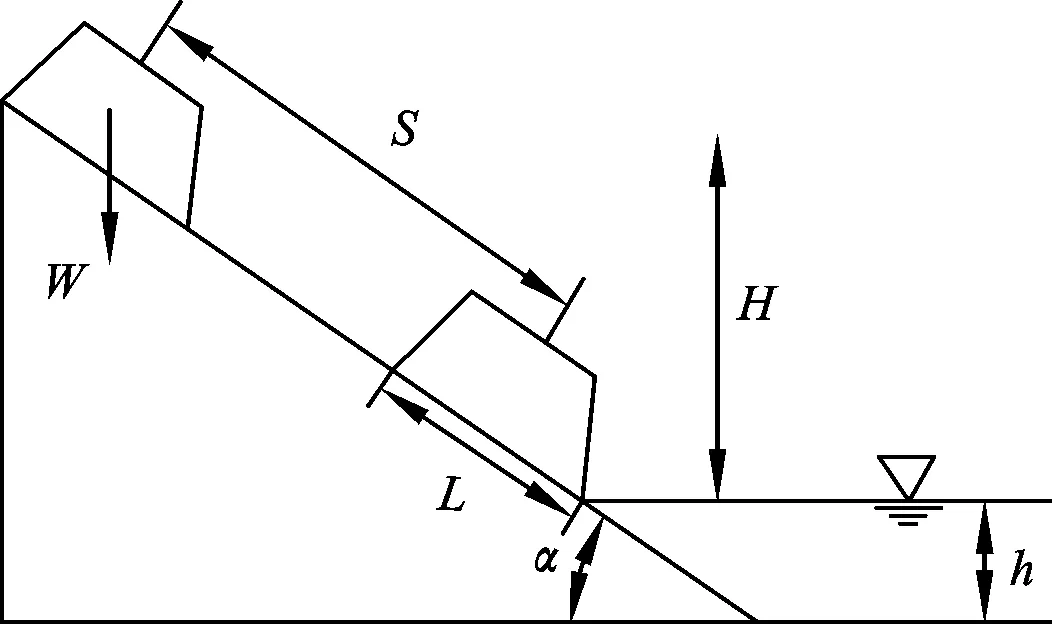
图13 滑坡体涌浪平均速度预测各要素Fig.13 The prediction factors of landslide surge average velocity

6.2 滑坡堵江分析与计算

滑坡进入河床完全堵塞河床需要有一定的体积。构成完全堵江的最小入江土石方量Vmin可通过计算获得。

假设滑坡物质入江方向与河水流向正交,河床宽Br,河水深Hr,河床坡降β,一般情况下β较小,可视为水平。天然坝上游坝体较陡,其坡度应满足堵江岩土体在饱水状态下的内摩擦角φs,下游坡度可采用堵江物质发生水石流的起始坡度,一般取14°,坝底宽度为Ld1,则完全堵塞河床所需的最小土石方量可简化为,如式(7)-(6)所示:

(3)

式中:Vmin为完全堵江所需的最小土石方量;Hr为河水深度(m);Br为河床宽度(m);φs为岩土体饱水状态下的内摩擦角(°)。

区内雅砻江水系年平均流量1 910 m3/s,Qs≥fr×Qr即可形成堵江事件。其中Qs(m3/s)为单位时间入江土石方量;Qr(m3/s)为河水流量;fr为岩土与河床间的摩擦角θ等有关的无因次量,当θ为5°～10°时,初步估算fr值在0.6～0.2间变化。

根据滑体所处江面几何特性及岩土体自稳能力计算,最小堵江体积方量约为605万m3。因1#、2#、3#次级滑体方量分别约为558.2万m3、50.7万m3、45.3万m3,所以次级滑体如整体滑动,不会形成堵江。

6.3 滑坡涌浪计算

当岸坡发生水平运动时,激起的初始浪高可表示为:

(4)

式中:ξ0为激起的初始涌浪高度(m);h为水库平均深度(m);v为岸坡水平运动速度(m/s);g为重力加速度(m/s2)。

当岸坡发生垂直运动时,激起的初始浪高可用下面的函数表示为:

(5)

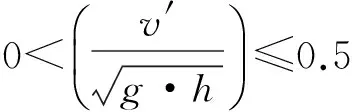
两种模式下的变化曲线如图14所示。

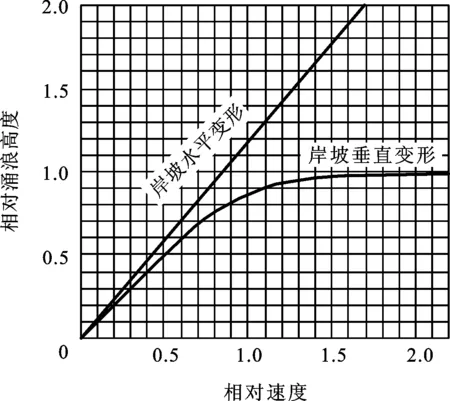
图14 两种模式下的初始涌浪高度求解曲线图Fig.14 The initial surge height in two modes curve

以滑坡失事点为扰动中心,结合推进波及孤立波传到对岸的反射波两者波型,利用波高按距离的倒数递减的规律(连续原理),计算出各小波直接传到水库某点的波高和反射波传到该点的波高,并把两者进行迭加,得出了滑坡失事点到对岸任意点的最高涌浪公式。其中滑坡涌浪传至对岸任一点产生的最大涌浪高度为:

(6)式中:ζ0为初始浪高(m);Ck为波的反射系数;x0为滑坡至A′的距离(m);L为滑坡体宽度(m);n为级数应取的次数;θn为第n次入射线与岸坡法线的夹角。

上述规范中研究了滑坡水平运动和垂直运动两种极端状态,实际中滑坡都是以一定倾角下滑入水。基于陈学德(1984)的建议方法,通过滑坡滑动面角度,对倾斜入水的滑坡所产生的最大涌浪高度进行修正。设滑坡沿着滑动面运动速度为v,滑动面倾角为∂,将速度进行矢量分解,则水平、垂直速度分别为:

vh=v·cos∂;vv=v·sin∂

应用上述计算公式分别计算水平运动和垂直运动产生的涌浪高度ηh、ηv,将两者分别乘以权重后叠加,则修正后的最大涌浪高度为:

η=ηh·cos∂2+ηv·sin∂2

(7)

涌浪计算结果如表2。

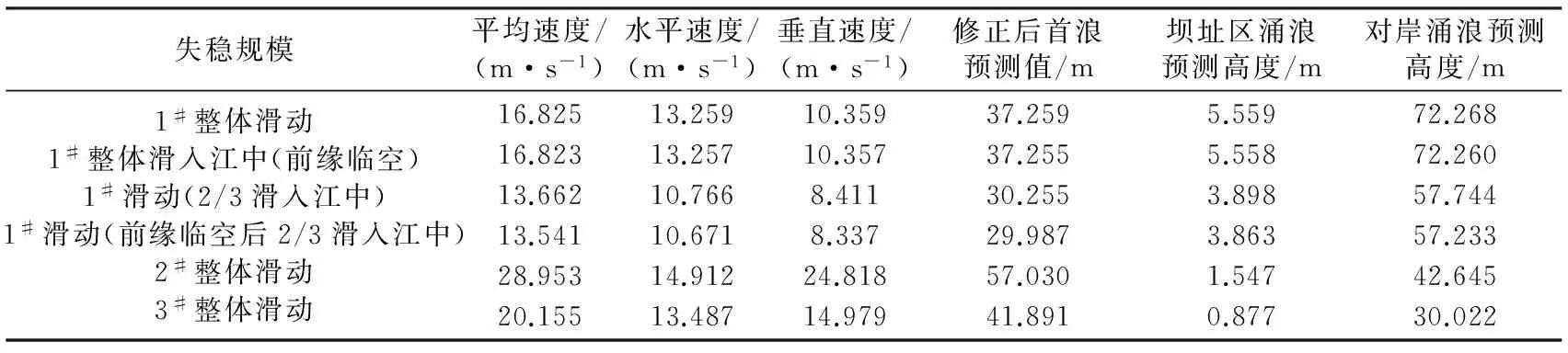
表2 涌浪计算结果Table 2 The surge calculation results

7 工程影响评价

根据麻日滑坡Ⅰ-Ⅰ剖面上2#次级滑体刚体极限平衡分析,认为其在不利工况下发生失稳的可能性较大,整体失稳后会产生约50万m3方量滑体,该方量滑体未达到雅砻江最小堵江方量,失稳后不会形成堵江。同样可知1#和3#次级滑体也不会形成堵江。

当1#次级滑体整体方量入江,失稳滑体滑动时平均速度为16.825 m/s,滑动产生的初始涌浪高度为37.259 m。涌浪传递至下游共科水电站坝址区5.8 km时,预测浪高为5.559 m。

当1#次级滑体前缘临空且整体方量入江,失稳滑体滑动时平均速度为16.823 m/s,滑动产生的初始涌浪高度为37.255 m。涌浪传递至下游共科水电站坝址区5.8 km时,预测浪高为5.558 m。

当1#次级滑体仅有2/3的方量入江,失稳滑体滑动时平均速度为13.662 m/s,滑动产生的初始涌浪高度为30.255 m。涌浪传递至下游共科水电站坝址区5.8 km时,预测浪高为3.898 m。

当1#次级滑体前缘临空且仅有2/3的方量入江,失稳滑体滑动时平均速度为13.541 m/s,滑动产生的初始涌浪高度为29.987 m。涌浪传递至下游共科水电站坝址区5.8 km时,预测浪高为3.863 m。

当2#次级滑体整体方量入江,失稳滑体滑动时平均速度为28.954 m/s,滑动产生的初始涌浪高度为57.03 m。涌浪传递至下游共科水电站坝址区5.8 km时,预测浪高为1.547 m。

当3#次级滑体整体方量入江,失稳滑体滑动时平均速度为20.156 m/s,滑动产生的初始涌浪高度为41.891 m。涌浪传递至下游共科水电站坝址区5.8 km时,预测浪高为0.877 m。

8 结论

根据相关现场勘查、室内统计资料,以麻日滑坡为研究对象,利用该区域的地理环境、气象水文、区域地质、新构造运动与地震等资料,对滑坡的边界、形态规模、变形破坏特征、组成滑坡系统的各个要素做出充分分析,其中包括滑坡的形成演化机制及后期的变形破坏特征,并进行了数值模拟验证。且对滑坡在各种工况下的稳定性进行了定性、定量的分析,综合评价了麻日滑坡的稳定性,为防治方案提供了理论依据。

[1] 中国电力企业联合会.水利水电工程地质勘察规范:GB 50287—2006[S]. 北京:中国计划出版社,2008.

[2] 李宁,郭双枫,姚显春.边坡潜在滑动面模拟方法研究[J].岩石力学与工程学报,2016,35(12):2377-2387.

[3] 曹琰波,戴福初,许冲,等.唐家山滑坡变形运动机制的离散元模拟[J]. 岩石力学与工程学报,2011,30(s1):2878-2887.

[4] 韩贝传,王思敬.边坡倾倒变形的形成机制与影响因素分析[J].工程地质学报,1999,7(3):213-217.

[5] 丰定祥,吴家秀,葛修润.边坡稳定性分析中几个问题的探讨[J].岩土工程学报,1990,12(3):1-9.

[6] 谷江波,柯善军,黄润太.黄金坪水电站边坡变形机制分析[J].水力发电,2016,42(3):20-23.

[7] 李攀峰,黄啸鹰,吴建川,等,溪洛渡水库运行期干海子滑坡变形动态响应研究[J].工程地质学报,2016,24(s1):996-1002.

[8] 李滨,王国章,冯振,等.陡倾层状岩质斜坡极限平衡稳定分析[J].岩土工程学报,2015,37(5):839-846.

[9] 黄波林,陈小婷,殷跃平,等.滑坡崩塌涌浪计算方法研究[J].工程地质学报,2012,20(6):909-815.

(责任编辑：费雯丽)

2017-06-15;改回日期:2017-06-22

邓卫东(1967-),男,教授级高级工程师,硕士,地质工程专业,从事水电工程地质、岩土工程、地下工程、水环境等领域的工作。E-mail:1989007@chidi.com.cn