基于事件触发机制的Markov跳变系统的量化保性能控制

熊伟伟，王惠姣

(浙江理工大学机械与自动控制学院，杭州 310018)

基于事件触发机制的Markov跳变系统的量化保性能控制

熊伟伟，王惠姣

(浙江理工大学机械与自动控制学院，杭州 310018)

根据事件触发机制，针对连续Markov跳变系统，研究了其量化保性能控制器的设计问题。为解决网络带宽有限问题，提高网络资源利用率，首先在采样器端引入一种离散事件触发机制，同时分别在状态反馈通道和控制输入通道设置对数量化器；然后运用时滞系统方法，建立新的Markov跳变系统模型；接着通过构造Lyapunov-Krasovskii泛函，得到了使闭环反馈系统渐进稳定且满足保性能指标的充分条件，并进一步设计了保性能控制器。该方法考虑了网络时延的影响，符合实际网络状况，通过设置事件发生器和对数量化器，有效降低了网络负载。仿真验证了该方法的有效性。

Markov跳变系统；事件触发机制；量化；保性能控制

0 引 言

Markov跳变系统(Markov jump systems，MJSs)是一类多模态系统，不同模态之间的转移通过Markov链的作用来实现，它可以描绘很多实际系统，如通信系统、经济系统、生物和医药系统等[1]，因此引起了学者们的广泛关注，在过去的几十年中已出现了大量文献，其中有对系统稳定性的分析，也有对H∞控制问题的讨论[2-6]。

同时，随着网络技术的快速发展，网络控制系统(networked control systems，NCSs)在现代工业领域有着广泛运用。在网络控制系统中，传感器信号和控制器信号通过公共的网络平台传输，然而实际中网络带宽是有限的。为了减少不必要的网络信号传输，节约网络资源，Arzen[7]提出了一种新方法，称为事件触发机制，其基本思想为：只有满足触发条件时控制任务才被执行。跟传统的时间触发机制相比，采用事件触发机制能有效减少数据传输。另一种解决网络带宽有限问题的方法是量化。近几十年来，学者们针对量化情况下不同的系统(线性系统和非线性系统)做了深入研究。如：Elia等[8]针对单输入单输出系统，在考虑状态量化的情况下，利用Lyapunov函数研究了系统稳定性；Xiao等[9]针对Markov跳变系统，利用扇形有界法讨论了量化对系统稳定性影响。但是，有限的网络带宽使得数据通过网络交换时会产生网络诱导时延、数据丢包及错序等现象。目前，针对网络化Markov跳变系统，许多学者采用不同的方法讨论了考虑网络时延情况下的H∞控制问题[10]和滤波问题[11]。然而这些成果大多是基于时间触发方式，不利于节约网络资源。

此外，保性能控制是一种在保证控制系统稳定的同时满足一定性能指标的控制方法。从现有文献来看，绝大多数关于保性能控制的文献都采用周期触发方式[12-14]，同时考虑事件触发和量化的文献甚少。虽然Hu等[15]在考虑量化及事件触发机制的影响下，研究了一类不确定线性连续网络控制系统的鲁棒镇定问题，但并没有考虑Markov跳变系统。

基于以上分析，本文针对Markov跳变系统，研究了事件触发机制下的量化保性能控制问题。首先为减少网络通道中的数据传输和提高有限网络资源的利用率，引入了一种离散事件触发机制；为提高数据传输能力，设置了对数量化器，然后通过时滞间隔分析法建立Markov跳变时滞系统模型，结合线性矩阵不等式分析了系统稳定性，并设计了保性能控制器；最后通过一个仿真验证了本文所提方法的有效性。

1 问题描述

1.1 系统描述

基于事件触发机制的网络控制系统结构框图如图1所示，其中被控对象假定为Markov跳变系统，方程描述如下：

(1)

其中：x(t)∈Rn为状态向量；u(t)∈Rm为系统的控制输入；Rn为n维向量空间；Rm为m维向量空间；A(r(t))和B(r(t))为与系统相应维数的定常矩阵；r(t)为一个取值于有限集S={0,1,2,…,s}的连续时间离散状态齐次Markov随机过程；记Markov概率转移矩阵为Π=(λij)(i,j∈S)；λij表示从模态i跳变到模态j的转移率，并且满足如下的条件：

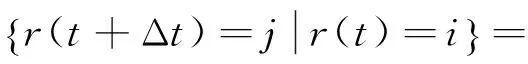
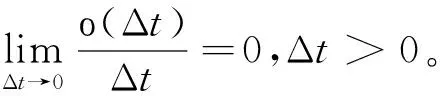
当r(t)=i∈S时，A(r(t))，B(r(t))分别记为Ai，Bi。

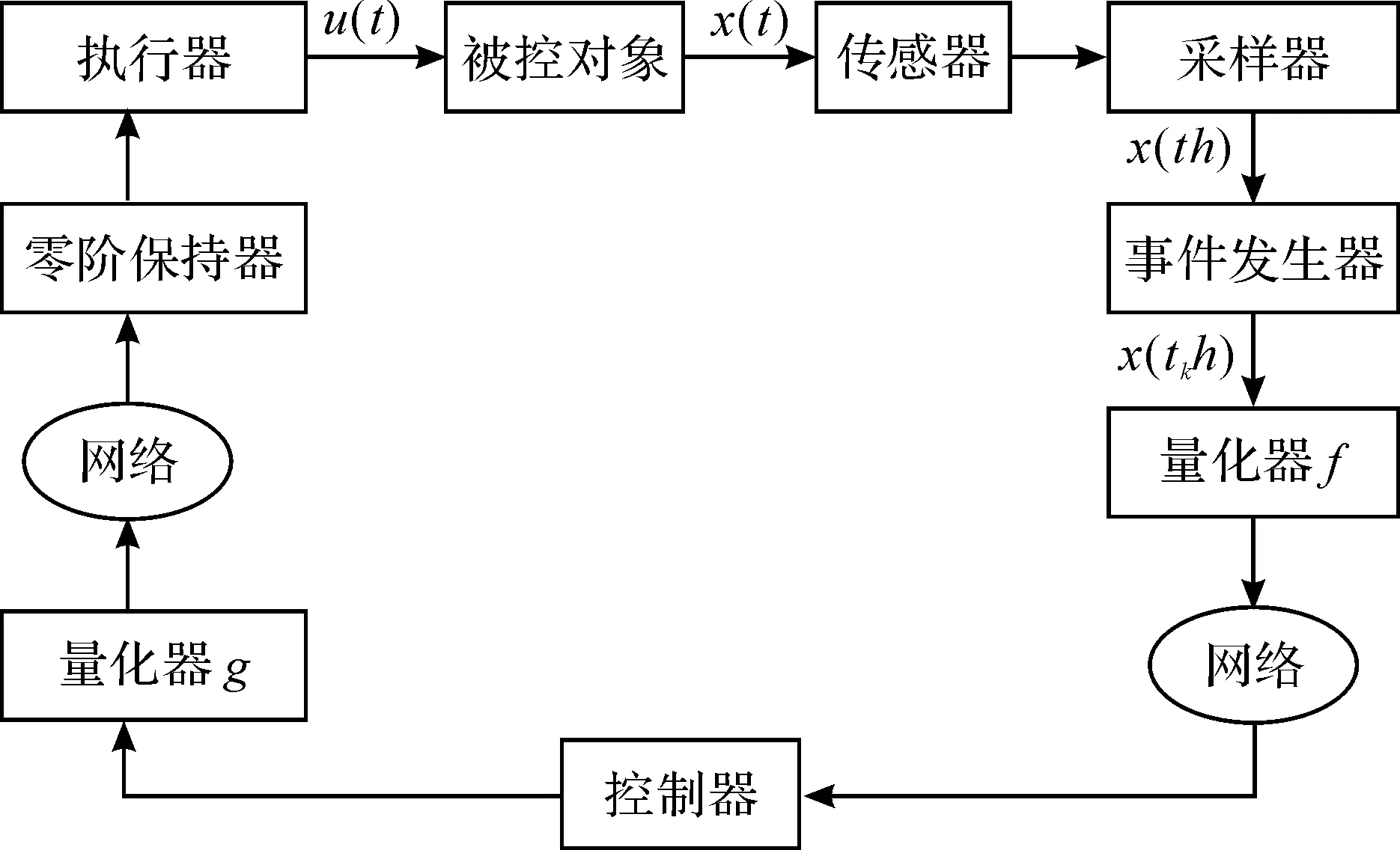
图1 事件触发网络化系统结构框图

为了简化研究，本文进行如下的设定：

a) 假设网络通道中数据单包传输，无数据包丢失[16]。

b) 被控系统的所有状态变量都是可测的[17]。采样周期为h，采样时刻记为sk，(k=0,1,2,…,∞)，即sk=kh。采样状态x(sk)在tk时刻由事件发生器传送给量化器，其中tk∈N。在采样器和控制器端引入对数量化器，分别记为fi和gi(i∈S)。为简单起见，设定不同子模态的量化器相同，即fi=f,gi=g.

本文将用到如下记号：

a) 在分块矩阵中，用I，0分别记单位矩阵和零矩阵，其阶数由适维性决定。

b) diag{a1,…,an}表示由元素a1,…,an构成的对角矩阵，符号*表示对称位置的块矩阵。

1.2 基于事件触发机制的系统模型

将系统(1)中当前状态记作x(kh)，传输出去的状态记为x(tkh)，那么只有满足以下关系的数据才能被传输：

(2)

其中：Φi为需要设计的正定对称加权矩阵；ε∈(0,1]为给定的常数参数。

(3)

其中：τtk为总的网络时延；Ki为带设计的状态反馈增益。

在采样器端，量化器f定义为f(x)=[f1(x1)f2(x2)…fn(xn)]T，其中对数量化器fs(xs)(s=1,2,…,n)定义为:

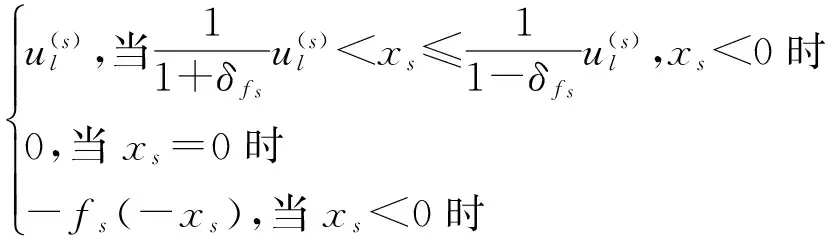
(4)

f(x)=(I+Δf)x

(5)

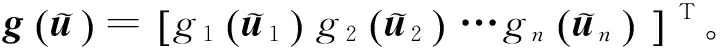
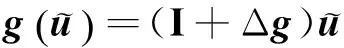
(6)

在本文中，为简便，假设δfs=δf，δgr=δg，其中δf和δg是两个常数。结合式(3)—(6)，考虑到零阶保持器的作用，得到:

u(t)=(Ki+ΔKi)x(tkh),t∈[tkh+τtk,tk+1h+τtk+1)

(7)

其中ΔKi=ΔgKi+KiΔf+ΔgKiΔf。把式(7)带入(1)，得到:

(8)

运用与文献[20]类似的方法，假设存在一个正整数q使得tk+1=tk+q+1，那么可以将区间[tkh+τtk,tk+1h+τtk+1)分割成q+1个子区间，表示如下:

(9)

其中:Ωn=[tkh+nh+τtk+n,tkh+(n+1)h+τtk+n+1),tk+1=tk+n+1。状态x(tkh),x(tkh+nh)，n=1,2,3,…,q满足:

[x(tkh+nh)-x(tkh)]TΦi[x(tkh+nh)-x(tkh)]≤εxT(tkh+nh)Φix(tkh+nh)

(10)

定义函数:

τ(t)=t-tkh-nh,t∈Ωn

(11)

可以容易得到时变时延取值范围：

另外，定义误差向量:

ek(t)=x(tkh+nh)-x(tkh),t∈Ωn

(12)

结合式(10)—(12)，当t∈[tkh+τtk,tk+1h+τtk+1)，得到:

(13)

由式(8)及(12)，得到闭环系统的状态方程:

(14)

其中φ(t)是x(t)的初始函数。

结合系统(1)，定义如下性能函数：

(15)

其中W和V是正定对称矩阵。

本文的主要任务是针对系统(1)，在事件触发机制(2)和量化(5)—(6)的作用下，设计一个状态反馈保性能控制器u*(t)，使得闭环系统(14)是稳定的，并且存在J*使得保性能函数值满足J≤J*。

2 主要结果

2.1 系统稳定性分析

定理1 给定参数0≤ε<1，τm，τM和状态反馈增益Ki，如果存在正定对称矩阵Pi>0，Q1>0，Q2>0，R1>0，R2>0，Фi>0(i∈S)，W>0，V>0及适当维数的矩阵M，N，满足以下的线性矩阵不等式：

(16)

其中：

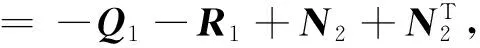
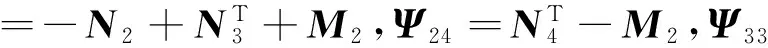
那么闭环系统(14)是渐进稳定的。

在定理1的推导过程中，本文通过引入自由加权矩阵来处理交叉项，减少了结果的保守性。

2.2 控制器设计

(17)

其中：

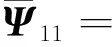
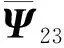
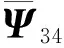
那么闭环系统(14)是渐进稳定的，且状态反馈保性能控制器为:

成本函数满足:

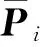
(18)

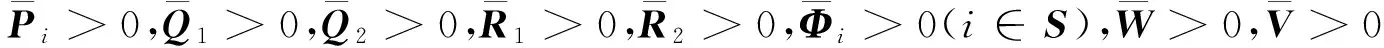
(19)

其中：

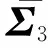
3 仿 真

假设系统(1)由两个模态构成：

模态1:

模态2：

状态转移概率矩阵为：

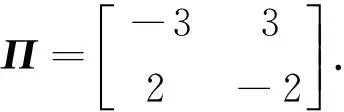
假设采样周期为h=0.10 s，初始条件为x0(t)=[0 0.10]T，W=diag{0.10 0.10}，V=1。为简单起见，假设两个对数量化器有相同的量化指标，即δf=δg=δ，并给定τM=0.01 s。根据定理3，通过简单的计算得到不同的触发系数ε与最大时延上界τM，30 s内数据传输的次数n及保性能值J*的关系，见表1。从表中可以看到触发系数ε越大，传输次数越小。

表1 不同的τM对应的不同其他值

给定触发系数ε=0.15,可以得到量化与最大时延上界τM的关系，结果如表2所示，结果显示，量化减小了最大时延上界τM，这意味着网络通讯负载减小了。

表2 不同的δ对应的最大时延上界τM

当ε=0.1，τM=0.5 s，δ=0.1时，根据定理3可以计算得到状态反馈增益为：

触发矩阵为：

如图2是系统模态转移图，由于跳变是随机的，这里只是给出了一种可能的模态切换情况。图3表示的是闭环系统的状态响应曲线图，从图中可以清楚地看到两条状态响应曲线最终趋于0，系统达到稳定状态。图4描述了数据在仿真期间的触发时刻，采样时间为30 s，采样300次，只有87个触发点，只占所有采样信号的29%，减少了数据发送率，说明本文的设计的方法效果良好。

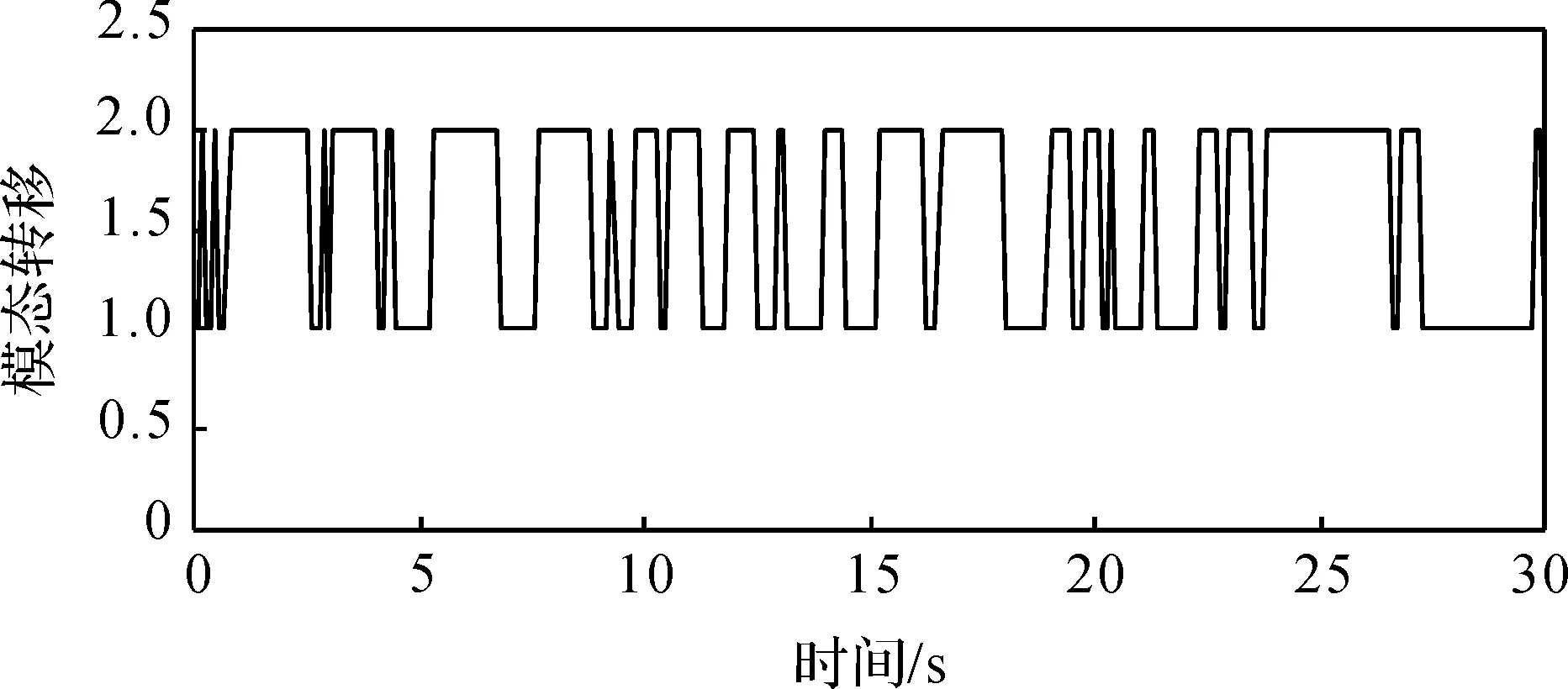
图2 模态转移图

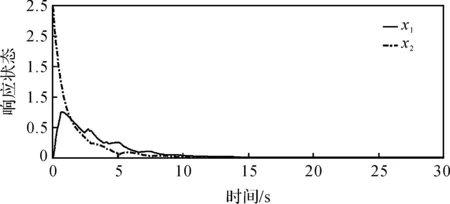
图3 闭环系统状态响应曲线

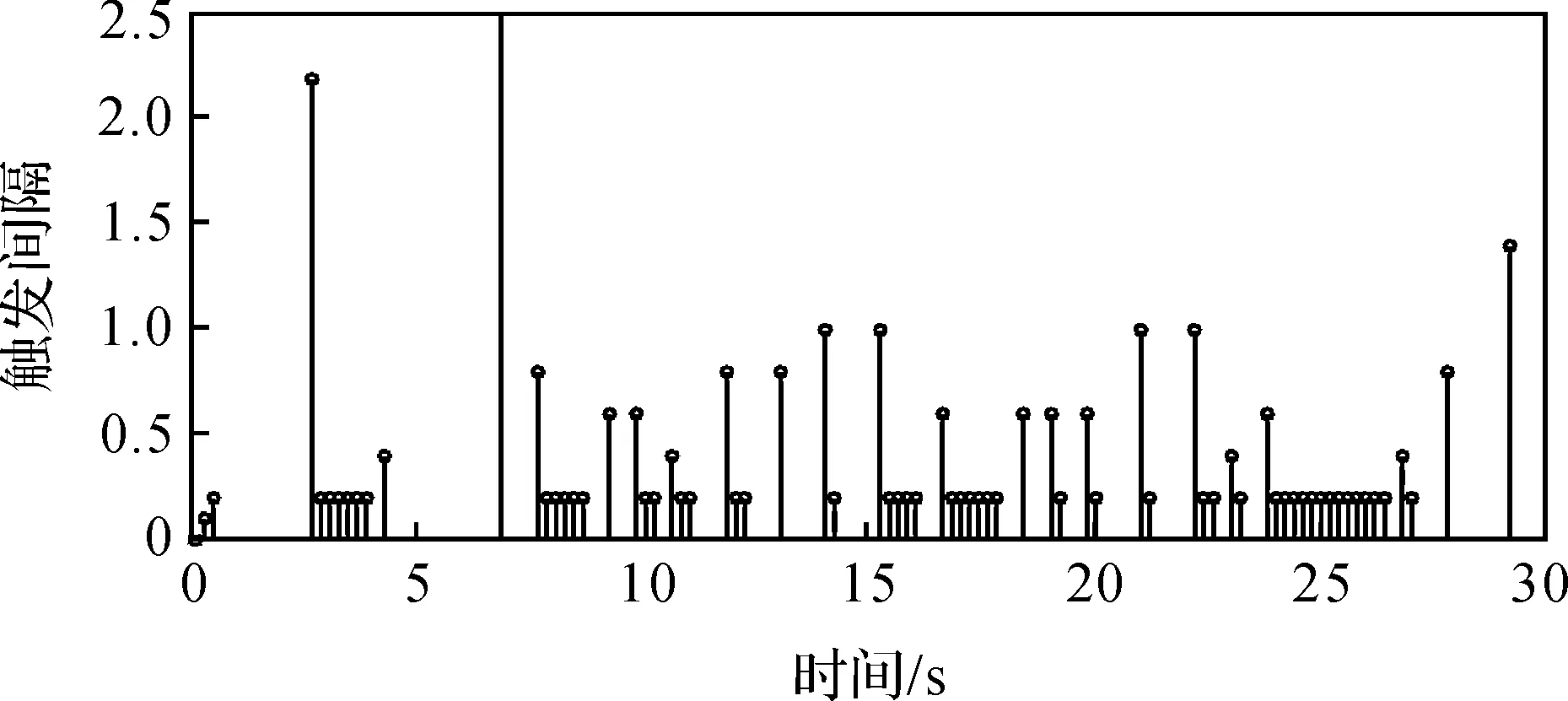
图4 事件触发时刻及触发间隔变化

4 结 论

本文考虑数据量化及时变传输时延的影响，同时引入事件触发机制，讨论了网络化Markov跳变系统的保性能控制问题。通过设置事件发生器和量化器，减少了数据传输率，减少了网络负载，并利用Lyapunov-Krasovskii泛函得到闭环系统稳定性条件，该条件同时刻画了时延、量化及事件触发参数之间的相互制约关系，根据该条件设计了保性能控制器。本文的研究解决了网络带宽有限的问题，设计的保性能控制器在保证系统稳定的同时保证系统的性能指标最优。仿真实例表明本文设计的方法提高了网络资源利用率。

[1] ZHANG L.H∞estimation for discrete-time piecewise homogeneous Markov jump linear systems[J]. Automatica,2009,45(11):2570-2576.

[2] FANG Y G, LOPARO K A. Stabilization of continuous-time jump linear systems[J]. Automatic Control IEEE Transactions on,2002,47(10):1590-1603.

[3] GOU N. Stochastic optimal tracking with preview for linear discrete-time Markovianjump systems[J]. Transactions of the Society of Instrument & Control Engineers,2009,24(6):144-153.

[4] WANG Z, LIU Y, YU L, et al. Exponential stability of delayed recurrent neural networks with Markovian jumping parameters[J]. Physics Letters A,2006,356(4/5):346-352.

[5] XU S, CHEN T Y. Robust control for uncertain discrete-time stochastic bilinear systems with Markovianswitching[J]. International Journal of Robust & Nonlinear Control,2005,15(5):201-217.

[6] DING Q, ZHONG M Y. On designingH∞fault detection filter for Markovian jump linear systems with polytopic uncertainties[J]. International Journal of Innovative Computing Information & Control Ijicic,2010,6(3):995-1004.

[7] ARZEN K E. A simple event-based PID controller[C]//Proceedings of the 14th IFAC World Congress. Beijing: IFAC,1999:423-428.

[8] ELIA N, MITTER S K. Stabilization of linear systems with limited information[J]. IEEE Transactions on Automatic Control,2002,46(9):384-1400.

[9] XIAO N, XIE L, FU M. Stabilization of Markov jump linear systems using quantized state feedback[J]. Automatica,2010,46(10):696-1702.

[10] WANG J, WANG H, XUE A K, et al. Delay-dependent [formula omitted]control for singular Markovian jump systems with time delay[J]. Nonlinear Analysis Hybrid Systems,2013,8(5):1-12.

[11] WANG Z, HO D. Filtering on nonlinear time-delay stochastic systems[J]. Automatica,2003,39(1):101-109.

[12] YUE D, PENG C, TANG G Y. Guaranteed cost control of linear systems over networks with state and input quantisations[J]. IEE Proceedings - Control Theory and Applications,2006,153(6):58-664.

[13] WU L, LAM J, YAO X, et al. Robust guaranteed cost control of discrete-time networked control systems[J]. Optimal Control Applications & Methods,2011,32(1):5-112.

[14] FRIDMAN E. Guaranteed-cost control of a linear uncertain system with multiple time-varying delays: an LMI approach[J]. IEE Proceedings-Control Theory and Applications,2003,150(1):7-22.

[15] HU S L, YUE D. Event-triggered control design of linear networked systems with quantizations[J]. ISA Transactions,2012,51(1):153-162.

[16] JIA X C, ZHANG D W, HAO X H, et al. FuzzyH∞tracking control for nonlinear networked control systems in T-S fuzzy model[J]. IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics,2009,39(4):1073-1079.

[17] PENG C, TIAN Y C. NetworkedH∞control of linear systems with state quantization[J]. Information Sciences,2007,177(24):5763-5774.

[18] YUE D, HAN Q L, LAM J. Network-based robustH∞control of systems with uncertainty[J]. Automatica,2005,1(6):999-1007.

[19] FU M Y, XIE L H. The sector bound approach to quantized feedback control[J]. IEEE Transactions on Automatic Control,2005,50(11):698-1711.

[20] HU S L, ZHANG Y N, DU Z. Network-basedH∞tracking control with event-triggering sampling scheme[J]. Control Theory & Applications Iet,2012,6(4):33-544.

(责任编辑： 康 锋)

Quantization Guaranteed Performance Control of Markov Jump System Based on Event-Triggered Mechanism

XIONG Weiwei, WANG Huijiao

(Faculty of Mechanical Engineering and Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China)

In this paper, the design of quantization guaranteed performance controller of continuous Markov jump system is studied according to event-triggered mechanism. To solve the problem of limited bandwidth, and improve the utilization ratio of network resources, a discrete event-triggered mechanism is adopted at the sampling apparatus, and logarithmic quantizers are set in the state feedback channel and the control input channel respectively; a new Markov jump system model is built with the time delay system approach; the sufficient conditions for gradually stabilizing the closed-loop feedback system and meeting the guaranteed performance index are obtained by establishing Lyapunov-Krasovskii functional, and a guaranteed performance controller is designed. Concerning this method, the influence of network delay is taken into account, which conforms to the actual situation of network, and network load is largely reduced by setting the event generator and logarithmic quantizers. The effectiveness of this method has been verified by means of simulation results.

Markov jump system; event-triggered mechanism; quantization; guaranteed performance control

10.3969/j.issn.1673-3851.2017.09.011

2017-05-21 网络出版日期： 2017-08-07

国家自然科学基金项目(61473264);浙江省自然科学基金重点项目(LZ17F030002)

熊伟伟(1991-)，男，浙江慈溪人，硕士研究生，主要从事事件触发网络控制方面的研究。

王惠姣，E-mail:hjwang@zstu.edu.cn

TP273

A

1673- 3851 (2017) 05- 0669- 07