试论现代经济中数学理论的应用
2017-09-03王盼
王盼
(延安大学 数学与计算机科学学院,陕西 渭南 716000)
试论现代经济中数学理论的应用
王盼
(延安大学 数学与计算机科学学院,陕西 渭南 716000)
社会的进步使得数学理论在现代经济中应用逐渐广泛,能够对经济行为进行有效指导。基于此,从经济学与数学的关系着手,对现代经济中数学理论的应用进行详细分析。
现代经济;数学理论;工具;函数
经济发展将降低生产成本、提高生产效率作为核心,所以,经济管理中需要对成本、收入、利润等问题给予足够重视。只有将产量与销量进行协调,才能保证使用最小的投入,获得最大的收益。在现代经济中科学应用数学理论,能够为经济管理提供有力的依据。
一、经济学与数学的关系
数学作为一门十分严谨的基础性学科,在贸易与金融中应用比较广。例如,经济学中的概率等问题,同样也是数学中重要的理论之一,即对经济行为中的不确定因素进行分析,对发展趋势进行预测,指导经济行为,做出科学决策;另外,还能概率描述净现金流、经济效果指标,对其中存在的风险进行评估。
随着社会的进步与经济的发展,现代经济中逐渐加强了数学理论的应用。在初期,数学理论的应用主要为比较初级的数学知识,并且范围比较局限,大多为政治经济学,多采用定量分析的方式。到19世纪时,数学逐渐加强与经济学的结合,数学中的概率、微积分等理论在经济学中逐渐流行起来。现阶段数学与经济学的结合已经相当成熟,大量新生理论出现,对经济学起到的促进作用不容忽视。很多数学工具应用到经济学中能够进行成本计算与产量设置等。例如,数学模型的应用使局部相对均衡的市场能够进行线形模型的建立,其中矩阵运算十分重要。该市场还能进行非线性模型的建立,其中一次方程和二次函数比较重要。现代信息技术的发展促进了数学与计算机的结合,两者的优势在企业经济决策中起着关键作用。经济决策人员合理运用数学工具能够将企业的成本控制到最小,并且制定出合理的价格。
现代经济学中应用的数学理论比较多样,能够起到良好的指导作用。在经济高速发展的同时,经济的决策者要意识到数学只是用于解决经济中出现的与数学有关的问题的工具,仍然要将工作重心放到经济而非数学上,在运用该种工具解决实际问题时,要使用科学的方式将其转化为数学相关问题,对其中存在的变量关系进行分析,形成对经济的指导作用。
二、现代经济中数学理论的应用
(一)现代经济中数学理论的应用可行性
现代经济学通过对社会资源进行优化利用,并且整合社会中人们的生产关系,使用各种手段对人与人、人与物质之间的价值关系进行处理。通过数学理论的合理应用,能够对经济行为中出现的数据进行规律分析与总结,确定出最优的实施方案,提高资源利用效率。
(二)现代经济中数学模型的应用过程
1.模型准备
首先调查先阶段的经济管理中需要解决的各种问题,获得比较明确的认识;然后对解决该种问题收集、整理,核对需要使用的数据,保证数据的完整与准确;再将收集到的数据与需要进行解决的问题进行结合,选取适用的数学模型,保证其与经济原型能够很好贴合。
2.模型假设
对需要解决的问题有着明确的认识,并且准备好相关数据后,使用选定的数学模型分析相关数据。在进行分析的过程中,要注意经济数据之间的关系,对其中存在的变量关系进行明确,然后提出假设。针对经济活动中的不同目的与不同要求,从收集到的数据中选取合适的数据,对其中有关因素进行讨论,保证结果的精确度。
3.建立模型
对现代经济中的问题制定合适的解决方式,然后将其转化为对应的数学语言,进行数学模型的建立与数据的求解,计算数学建模。在进行建模时,要先分析数据,安排其中的相应变量类型;再将有关的数学计算公式插入其中,对数据变化进行分析,保证所建数学模型的精确性。
4.模型求解
使用合适的数学计算工具与计算方式,对数学模型进行针对求解,并且与现代经济管理中的问题相结合,将数据结果作为依据,进行有关方案的选择
5.分析与应用模型
使用数学模型能够得出精确的结果,对结果进行分析,能够对有关经济变量中的各种关系的规律进行总结,最终确定出合适的方案,对经济行为进行科学指导。
(三)现代经济中数学模型的应用需要注意问题
在进行建模的过程中,要加强对经济管理数据与数学建模之间能否紧密结合的重视。将实际情况与理论知识进行联系,结合现代经济学的特点进行分析。
1.数学模型只针对于经济问题
对现代经济管理中的数据变量性质与关系进行分析,对数学理论基础中的概念模式进行构建,但是要注意只能对数据结果进行使用与帮助,不能分析数据的经济内涵。
2.严格测定能够量化的经济问题的数据
在对经济管理中出现的问题进行处理的过程中,需要结合数学模型中使用的数据与有关概念,从经济量的角度进行,不应该与数学模型中的经济本性相脱离。
3.牵涉到需要研究的经济数据
对现代经济管理中的统计进行研究,将其中包含的能够用于数学模型的数据抽离出来。数据的选取具有关键作用,针对模型的需要对数据进行取舍,也是提高数据精确性的过程。
3)____The popular images for Christmas are Christmas trees,Santa Claus,wreaths,candy canes and reindeer.
4.主经济数据的时空限定
对现代经济管理中数据产生的状态与特征进行研究,需要注意在选取数据的过程中,考虑到数据的时空限定,最终确定合适的数学模型。
5.处理数学模型得出的结果
数学模型的计算能够得出一定的数值,在分析数值时要根据有关的经济理论进行。根据这些结果制订对应的经济方案,对经济行为进行指导。
(四)现代经济中数学理论的具体应用
1.生产决策中数学理论的应用
保证生产量与销量之间关系的科学合理是企业长期稳定发展的关键。假如某个企业月销售额为50万元,毛利率为8%,那么每个月能够获得多少毛利。在解决这个问题时,选择合适的数学理论知识,使用数学公式对该问题进行转化。假设毛利率处于理想状态,毛利与销售额为正比关系,即销售额与毛利率相乘即为毛利,则毛利的具体计算为X=50×8% =4万元。使用高数中的函数与极限理论等,能够对企业最佳生产量进行指导。该企业某一月生产A与B两种产品,A产量为40吨,B产量为50吨,该月计划按照该比例将总生产量提高到160吨,则A与B两种产品各应该生产多少。设A产品产量为a,B产品产量为b,则40÷(40+50)=a÷160,a=71.11吨,所以b为88.89吨。由此可见,数学理论可以企业产量的设计进行科学指导,提高决策的科学性与准确性。
企业的成本支出通常分为固定成本与可变成本支出。固定成本主要为设备采购费用、对外宣传费用、固定资产采购费用等。相较于固定成本而言,可变成本具有一定的不确定性,主要根据实际需要进行。可以使用数学中线性代数相关知识对生产量与成本进行呈现。总成本为固定成本与可变成本的和,可变成本为单个产品的成本与产量的乘积,即总成本等于单个产品的成本与产量的乘积加上固定成本的和。数学中一次函数能够对其进行表述。将总成本设置为y,总产量为x,单位产品的可变成本设置为a,规定成本设置为c,则y=ax+c。假如企业固定成本为1 000元,产品成本为5.5元,那么计算生产1 500个产品需要多少总成本。使用该公式能够对该问题进行解决,即为y=5.5×1 500+1 000=9 250元。由此可见,运用合理的数学知识能够计算企业的成本问题,促进企业发展。
三、盈亏转折中数学知识的应用
盈亏转折能够有效促进企业的发展,实现经济效益的提高。虽然企业专业的管理与丰富的经验有利于该阶段的安全过渡,但是仍然需要使用合适的数学知识对销售收益进行保证,把握好收入与成本之间的差额。假若某个企业固定成本为6 000元,每天最多能够生产的产品数量为15 000件,当单价定位8元时,能够将产品全部卖出。当每件产品生产成本增加0.6元时,需要如何设定产量才能保证生产企业不发生亏损。使用数学公式很容易得出。将这个产品数量设置为x件,则y=0.6x+6 000,2x=0.6x+6 000,得出x值为4 286件。
四、现代经济中需求函数的应用
加入除了商品本身的价格以外,其他能够对需求量产生影响的因素处于理想状态,将市场需求量设为y=f(x),即为需求函数,线性函数就是最简单的需求函数。y=ax+b。假若某企业生产仪器,当单价为每件800元时,能够销售7 000件,当单价为每件750元时,能够销售9 000元,则对该函数进行确定,即为x为800时,y为7 000,当x为750时,y为9 000。将这两组数值代入函数中对函数进行确定。
五、在经济尺度中幂函数的应用
在进行经济的分析与决策中,经常出现经济尺度等问题。此时就需要用到数学理论中的幂函数对其进行确定。将经济活动中总的生产成本设置为y,企业的生产能力设置为x,其中的a与b为常数,进行幂函数的建立,即为y=axb。
图1中,当b值大于0小于1时,表示在工厂刚刚起步时,需要投入较多的成本;当生产能力达到一定程度,即为x点时,需要的成本投入相对减少,速度也逐渐放慢,表示生产力有所提高,成本逐渐减少,表明企业能够实现稳定发展。
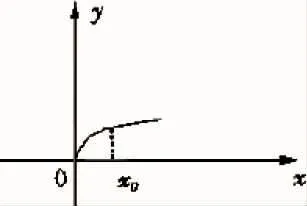
图1
图2中,b值大于1,表示在工厂刚刚起步时,需要投入较多的成本,当生产能力达到一定程度,即为x点时,成本的增长速度却大于生产能力的增长,这说明该企业不能实现健康发展,在经营中较为失败。

图2
由于指数b能够判断企业建设是否成功,所以称之为经济尺度指数。例如,当某电厂的基本建设成本为y=1.3xb(百万),其中x为发电能力,单位与兆瓦,当x值为900时,y值为150,判断该厂建设是否成功。对此进行计算即可,当b值大于0小于1时,表明建设成功;当b值大于1时,表明建设失败。
结语
首先对经济学与数学的关系进行阐述,然后指出现代经济中数学理论的应用可行性、使用数学建模的过程以及其中需要注意的问题,最后对成本计算中函数知识的应用、成本计算中函数知识的应用、盈亏转折中数学知识的应用、现代经济中需求函数的应用、在经济尺度中幂函数的应用进行举例说明。使用数学建模与数学理论能够对原本复杂的经济知识进行转化,提高变量对成本、收益影响计算的简便性,为企业经济决策提供依据。
[1]唐亚娜.关于数学理论在现代经济领域中的应用研究[J].科研,2016,(12):00026-00026.
[2]高珊珊.试论数学理论在现代经济中的应用[J].商,2016,(18):126-126.
[3]冷萤征.探讨数学在经济发展中的地位及作用[J].决策与信息旬刊,2016,(1):40-40.
[4]王兆钰.浅议数学统计方法对现代经济社会的作用[J].经济管理:全文版,2016,(6):00241-00241.
[5]李鹏.论高等数学理论在经济领域中的应用[J].科研,2015,(4):257-258.
[6]李学林,刘碧辉.经济学原理在人才培养中数学能力培养的研究[J].经济研究导刊,2016,(11):79-80.
[责任编辑 柯 黎]
F016;F224
A
1673-291X(2017)23-0149-03
2017-04-18
王盼(1986-),女,陕西渭南人,硕士研究生,讲师,从事数学课程与教学论研究。
