军用危险品航空运输装卸保障风险预测
2017-09-03颉正阳陈思杨
颉正阳,安 红,陈思杨
(空军勤务学院a.学员一大队;b.基础部;c.航空军交运输指挥系,江苏徐州221000)
军用危险品航空运输装卸保障风险预测
颉正阳a,安 红b,陈思杨c
(空军勤务学院a.学员一大队;b.基础部;c.航空军交运输指挥系,江苏徐州221000)
针对军用危险品航空运输装卸保障过程中的风险问题,根据军用危险品航空运输装卸保障理论与实际,梳理出影响军用危险品航空运输装卸保障的因素,建立了影响因素层次模型。针对影响因素的不确定性,将模糊集理论应用到贝叶斯网络中去,建立了基于模糊贝叶斯网络的军用危险品航空运输装卸保障风险预测的数学模型。最后,将实例中的节点证据输入到模糊贝叶斯网络中,对保障风险进行推理,验证了模型的有效性和实用性。
风险预测;军用危险品;航空运输;装卸保障;模糊贝叶斯网络
随着大型军用运输机的部队列装,军用危险品的航空运输也迎来了新的发展契机,但是,由于军用危险品的危险性,在其航空运输的保障过程尤其是装卸飞机过程中容易发生安全事故,造成人员和财产的损失。因此,有必要对军用危险品航空运输装卸保障的风险进行预测,以便提前采取预防措施。
贝叶斯网络,又称信度网络,是目前不确定知识表达和推理领域最有效的理论模型之一[1],它用清晰的具有网络结构的有向图表达各个信息要素之间的关联关系及影响程度,用节点变量表达各个信息要素,用连接节点之间的有向弧反映各个信息要素之间的关联关系,用条件概率表表达各信息要素之间的影响程度。贝叶斯网络具有强大的不确定知识的表达能力和灵活的推理机制,被广泛应用于军事决策[2]、故障诊断[3-4]、态势评估[5]、风险评估[6]等领域。但是,贝叶斯网络利用经典二值概率论表征节点变量,不能有效反映各信息要素的模糊性[7]。文献[8]利用模糊集合理论对连续型态势变量进行变参数模糊化,建立了无人机中远距空战战术决策的模糊贝叶斯网络模型。文献[9]以事故树模型为基础,映射为贝叶斯网络,采用梯形模糊数代替基本事件的概率,通过贝叶斯网络的正反向推理分析各基本事件的结构重要度、概率重要度、关键重要度,并进行排序,有效地定量评估了铁路危险货物运输过程中的风险性。本文针对军用危险品航空运输装卸保障过程中的各节点信息的连续性和模糊性,建立了模糊贝叶斯网络的军用危险品航空运输装卸保障风险预测模型,通过推理得出军用危险品航空运输装卸保障发生风险问题的概率值,使得采取保障安全措施有了针对性,提高了装卸保障的安全性和保障效率。
1 军用危险品航空运输装卸保障风险影响因素
军用危险品航空运输装卸保障风险影响因素层次模型,如图1所示。
影响军用危险品航空运输装卸保障风险的因素从总体上来说分为军用危险品自身因素和航空运输装卸保障因素。军用危险品自身因素主要指军用危险品自身的技术性能(理化性质)、包装、装卸性(指军用危险品对航空运输吊装吊卸、升降装卸、滚装滚卸和牵引装卸的适应性)。而航空运输装卸保障因素主要包括装卸保障作业能力、装卸保障指挥与信息控制、装卸保障配套建设以及装卸保障标准法规和技术支持。
在遵循科学性、可靠性、全面性、实用性和代表性的原则的基础上,并结合部队实践和专家的意见,经过综合考虑与分析,从人员、装备、计划管理、装卸作业和军用危险品5个方面建立了军用危险品航空运输装卸保障风险影响因素之间的层次关系。
2 风险预测的模糊贝叶斯网络模型
2.1 模糊贝叶斯网络概述
模糊贝叶斯网络[10-12]基本思想是利用模糊集对连续变量进行严密和一致的描述,再利用贝叶斯网络进行模糊节点变量的概率推理,即预测。假定问题有限的节点变量集用来表示,ci的所有可能状态集用Ci表示,再假设ci∈C可以被模糊化为一个模糊变量ui,并且ui可以表示ci的所有可能状态,则ci的模糊集为:
式(1)中:ri为 ui的模糊状态数;C͂ij表示ui的第 j个模糊状态。
在给定节点ci的父节点条件下,节点ci与父节点之外的其他节点条件独立,即[13-15]
式(4)中:π(ci)为节点ci的父节点集合;A(ci)为节点ci父节点之外的其他节点集合。
2.2 模糊贝叶斯网络模型的建立
2.2.1 贝叶斯网络的确定
参照图1所示的影响因素之间的层次关系,兼顾贝叶斯网络推理的复杂程度,构建了如图2所示的军用危险品航空运输装卸保障风险预测的贝叶斯网络结构。构建的基本思路是:以“风险预测”为目标节点,设为D。以“人员因素”、“装备因素”、“计划管理因素”、“军用危险品因素”和“装卸作业因素”为父节点,考虑到“人员因素”中有相同属性的节点变量,设置一个新的节点变量“操作人员因素B11”,包含“操作人员技术水平”和“操作人员编配率”。以c1,c2,…,c16为叶节点,作为贝叶斯网络推理时的证据节点。
2.2.2 网络节点变量参数模糊化
图2所示的贝叶斯网络结构中的节点变量代表的影响因素分为定性因素和定量因素。定性因素包括“指挥人员能力素质”、“保障装备技术性能”等,采用专家打分的方式确定因素值;定量因素包括“操作人员编配率”、“保障装备故障率”等,根据部队实际情况获取因素值。
影响因素分为正向因素和负向因素,正向因素指数值越大越好的因素,比如“装卸方案完善程度”;负向因素指数值越小越好的因素,比如“保障装备故障率”。
正向因素和负向因素的标准化公式分别为[16]:
式(6)、(7)中:cmk为第m个预测对象第k个节点变量的实测数值;分别为 p个预测对象中节点变量实测数值的相对最优值。
将图2中的节点变量划分模糊状态集,如目标节点的模糊状态集为{高,中,低},“人员身体状况”节点的模糊状态集为{好,中,差},“保障装备配套率”节点的模糊状态集为{高,中,低}。确定了各节点变量的模糊状态集后,还需要确定每个节点变量的模糊隶属函数。设各节点变量对应的模糊状态集中的元素分别为 ~Ci1、~Ci2和 ~Ci3,为使用方便且具有一般性的特点,选用梯形模糊隶属函数来描述各节点变量的隶属度[17],模糊隶属函数如图3所示。
由图3可知,节点变量的模糊隶属函数分别为:
由于节点变量的模糊状态集和节点变量的离散状态是一一对应的,因而根据模糊隶属函数得到的隶属度就等同于节点变量值属于各个模糊状态的概率值,这也符合模糊贝叶斯网络输入的证据状态是多态的实际情况。
2.2.3 网络节点变量的条件概率
采用德尔菲法[18]确定各节点变量的条件概率表,这里给出“操作人员因素”节点变量的条件概率表,作为模糊贝叶斯网络推理的先验信息,如表1所示,其他的节点变量的条件概率表限于篇幅不再一一列出。
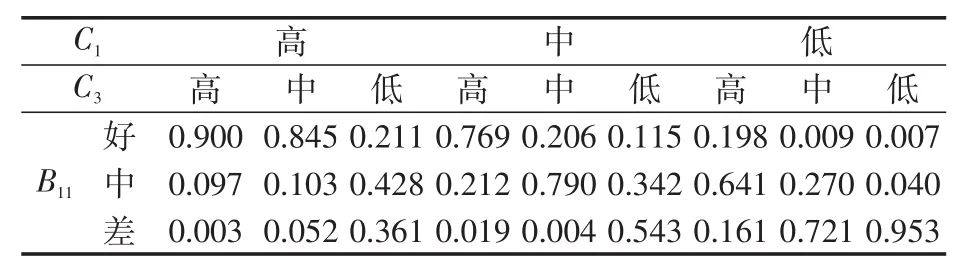
表1 “操作人员因素”节点变量条件概率表Tab.1 Conditional probability table of“operating personnel”
2.2.4 模糊贝叶斯网络的推理
模糊贝叶斯网络推理就是在模糊贝叶斯网络模型的基础上,根据先验信息,利用贝叶斯概率中条件概率的计算方法,计算出目标节点的概率。
经节点变量模糊化、推理得到的隶属函数是目标节点相应的概率值,故不再需要解模糊化的步骤[8]。风险预测即模糊贝叶斯网络推理过程如图4所示。
在获得节点变量值后,将其模糊化得到各节点变量的隶属度作为概率值,利用Matlab软件中的FullBNT工具箱建立模糊贝叶斯网络,将各节点变量的概率值输入贝叶斯网络进行概率推理,最后得到军用危险品航空运输装卸保障风险预测概率值。
3 实例分析
以某场站即将参加大型演习进行的军用危险品航空运输装卸保障为例,对该场站军用危险品的装卸保障风险进行预测,将风险分为3级(高、中、低)。
3.1 节点变量值的获取
根据该场站航空运输装卸保障和所运军用危险品的相关数据,结合其他几个场站相应节点变量的数据以及专家的打分,由式(6)、(7)得到各叶节点变量的标准化值,如表2所示。

表2 模糊贝叶斯网络叶节点变量标准化值Tab.2 Standardized values of node variables in fuzzy Bayesian network
3.2 节点变量模糊化
将模糊贝叶斯网络中各叶节点变量的标准化值代入隶属函数,得到隶属度即模糊状态概率值。由式(8)~(10)可得叶节点变量属于各模糊状态的隶属度,如表3所示。

表3 各叶节点变量隶属度Tab.3 Subordinate degrees of node variables
3.3 模糊贝叶斯网络推理
将叶节点变量证据模糊化后输入模糊贝叶斯网络进行概率推理,得到风险(高、中、低)发生的概率如表4所示。根据模糊贝叶斯网络的推理结果可知,该场站参加本次大型演习所要进行的军用危险品航空运输装卸保障风险预测值为中等风险,仍有19.4%的概率为高风险。分析B1~B4节点的推理概率可知,造成风险较高的原因在于场站对军用危险品的航空运输装卸保障没有配套的装卸装备;装卸相关人员没有经过针对军用危险品的专门培训;最重要的是,对于军用危险品的技术性能不了解,影响了装卸安全。该场站在演习前要抓紧对装卸保障人员进行相关知识的培训,并向上级申请装卸保障所需装备,以保证演习安全进行。

表4 模糊贝叶斯网络推理结果Tab.4 Fuzzy Bayesian network reasoning results
4 结论
充分考虑了军用危险品航空运输装卸保障过程中的不确定性,将模糊数学的理论与贝叶斯网络相结合,首次建立了军用危险品航空运输装卸保障风险预测的模糊贝叶斯网络模型,通过模糊贝叶斯网络的推理得到了风险预测概率值,推理结果较为可信,为部队进行军用危险品航空运输装卸保障的风险预测以及风险控制提供了借鉴。但也存在以下问题,需要在今后进行更进一步的研究。
1)条件概率表是基于德尔菲法给出的,主观性较大,影响了风险预测的精度,下一步可以引入客观的观测数据,采取参数学习的方式确定各节点变量的条件概率表;
2)定性因素值的获取,依靠的是专家打分,可能无法精确真实地反映实际情况,下一步可以研究定性因素的值如何获取更加准确。
[1]李硕豪,张军.贝叶斯网络结构学习综述[J].计算机应用研究,2015,32(3):641-645.LI SHUOHAO,ZHANG JUN.Review of bayesian networks structure learning[J].Application Research of Computers,2015,32(3):641-645.(in Chinese)
[2]赵飞,王青山,赵海涛.基于模糊贝叶斯网络的空降场选择研究[J].信息工程大学学报,2014,15(6):664-665.ZHAO FEI,WANG QINGSHAN,ZHAO HAITAO.Airhead selection based on the fuzzy bayesian network[J].Journal of Information Engineering University,2014,15(6):664-665.(in Chinese)
[3]WANG Y F,XIE M.Approach to integrate fuzzy fault tree with bayesian network[J].Procedia Engineering,2012,45:131-138.
[4]HUANG Y,MCMURRAN R,DHADYALLA G.Probability based vehicle fault diagnosis:Bayesian network method[J].Journal of Intelligent Manufacture,2008(19):301-311.
[5]王玉惠,韩占朋,陈哨东,等.防空态势评估系统分析及新型评估模型研究[J].南京航空航天大学学报,2014,46(4):558-560.WANG YUHUI,HAN ZHANPENG,CHEN SHAODONG,et al.Analysis and modeling of threat evaluation system in air defense operations[J].Journal of Nanjing University of Aeronautics&Astronautics,2014,46(4):558-560.(in Chinese)
[6]刘瑛,李敏强,陈富赞.飞行器机动动作风险定量评估模型[J].系统工程与电子技术,2014,36(3):469-472.LIU YING,LI MINQIANG,CHEN FUZAN.Risk quantitative evaluation model of the aircraft maneuver[J].Systems Engineering and Electronics,2014,36(3):469-472.(in Chinese)
[7]杨铭,郑寇全,雷英杰.基于直觉模糊贝叶斯网络的不确定性推理方法[J].火力指挥与控制,2015,40(3):37-38.YANG MING,ZHEN KOUQUAN,LEI YINGJIE.Method of uncertain reasoning based on IFBN[J].Fire Control&Command Control,2015,40(3):37-38.(in Chinese)
[8]耿文学,孔繁峨,马东前.基于模糊贝叶斯网络的UAV中远距空战战术决策[J].火力与指挥控制,2014,39(3):99-101.GENG WENXUE,KONG FANE,MA DONGQIAN.Method of uncertain reasoning based on IFBN[J].Fire Control&Command Control,2014,39(3):99-101.(in Chinese)
[9]杨能普,杨月芳,冯伟.基于模糊贝叶斯网络的铁路危险货物运输过程风险评估[J].铁道学报,2014,36(7):8-14.YANG NENGPU,YANG YUEFANG,FENG WEI.Risk assessment of railway dangerous goods transport process based on fuzzy bayesian network[J].Journal of the China Railway Society,2014,36(7):8-14.(in Chinese)
[10]周源,燕军,孙媛,等.基于贝叶斯网络的要地防空目标威胁评估模型[J].海军航空工程学院学报,2015,30(5):467-471.ZHOU YUAN,YAN JUN,SUN YUAN,et al.Threat evaluation air defense based model for important place on bayesian network[J].Journal of Naval Aeronautical and Astronautical University,2015,30(5):467-471.(in Chinese)
[11]贺小亮,毕义明.基于贝叶斯网络的目标选择方案设计[J].现代防御技术,2014,42(3):7-10.HE XIAOLIANG,BI YIMING.Target selection scheme design based on bayesian networks[J].Modern Defence Technology,2014,42(3):7-10.(in Chinese)
[12]纪军,田淑荣,马培蓓.基于动态贝叶斯网络的防空作战态势分析[J].海军航空工程学院学报,2013,28(8):679-682.JI JUN,TIAN SHURONG,MA PEIBEI.Situation analysis of air defensive operation based on dynamic bayesian network to object assessment[J].Journal of Naval Aeronautical and Astronautical University,2013,28(8):679-682.(in Chinese)
[13]陈东宁,姚成玉.基于模糊贝叶斯网络的多态系统可靠性分析及在液压系统中的应用[J].机械工程学报,2012,48(16):175-176.CHEN DONGNING,YAO CHENGYU.Reliability analysis of multi-state system based on fuzzy bayesian networks and application in hydraulic system[J].Journal of Mechanical Engineering,2012,48(16):175-176.(in Chinese)
[14]郝学良,朱小冬,赵劲松.模糊推理在软件维护性评估和预测中的应用[J].军械工程学院学报,2013,25(1):10-13.HAO XUELIANG,ZHU XIAODONG,ZHAO JINSONG.Application of fuzzy inference in software maintainability assessment and prediction[J].Journal of Ordnance Engineering College,2013,25(1):10-13.(in Chinese)
[15]王玉惠,韩占朋,程哨东,等.防空态势评估系统分析及新型评估模型研究[J].南京航空航天大学学报,2014,46(4):558-565.WANG YUHUI,HAN ZHANPENG,CHENG SHAODONG,et al.Analysis and modeling of threat evaluation system in air defense operations[J].Journal of Nan-jing University of Aeronautics&Astronautics,2014,46(4):558-565.(in Chinese)
[16]冯世豪,张立海,张百成.基于灰色模糊理论的军械仓库安全评估[J].海军航空工程学院学报,2016,31(2):185-188.FENG SHIHAO,ZHANG LIHAI,ZHANG BAICHENG.Ordnance depot of safety evaluation based on grey fuzzy theory[J].Journal of Naval Aeronautical and Astronautical University,2016,31(2):185-188.(in Chinese)
[17]董彦军,夏秀峰.基于模糊综合评判的航空备件需求预测[J].飞机设计,2014,34(6):66-70.DONG YANJUN,XIA XIUFENG.Demand prediction for spare parts of aviation eased on fuzzy comprehensive evaluation[J].Airgraft Design,2014,34(6):66-70.(in Chinese)
[18]SCHMIDT R,LYYTINEN K,KEIL M,et al.Identifying software project risks:an international delphi study[J].Journal of Management Information Systems,2001,17(4):5-36.
Risk Prediction of the Loading and Unloading Guarantee of Military Dangerous Materials Air Transportation
XIE Zhengyanga,AN Hongb,CHEN Siyangc
(Air Force Logistics College a.Cadet Brigade 1;b.Department of Basic;c.Department of Airway Military Transportation Command System,Xuzhou Jiangsu 221000,China)
Aiming at the risk during process of the loading and unloading guarantee in military dangerous materials air transportation,the influencing factors of the loading and unloading guarantee in military dangerous materials air transporta⁃tion were teased out based on the theory and reality of the loading and unloading guarantee,with building a hierarchical model of the influencing factors.For the uncertainty of the influencing factors,fuzzy set theory was applied to the Bayesian network,and the mathematical model of risk prediction in the loading and unloading guarantee in military dangerous mate⁃rials air transportation.Finally,the evidences of nodes in a case study were input into the fuzzy Bayesian network,reason⁃ing the risk of support and testing the validity and practicality of the model.
risk prediction;military dangerous materials;air transportation;loading and unloading guarantee;fuzzy Bayes⁃ian network
E234
A
1673-1522(2017)03-0313-06
10.7682/j.issn.1673-1522.2017.03.011
2017-03-16;
2017-05-17
国防科研基金资助项目(BJJ16L011)
颉正阳(1993-),男,硕士生。
