全桥LLC谐振变换器的参数分析与研究

黄森+刘军+徐忠良+唐刚

摘 要：全桥LLC谐振变换器以软开关、高效率等特性，广泛应用在中大功率DC/DC变换器。文章详细分析了全桥LLC谐振变换器拓扑的工作原理，并运用基频分量法讨论了L、C等参数对谐振变换器的影响。结果分析表明，励磁电感Lm选取较大值时，变换器的传输损耗较小。

关键词：LLC谐振变换器；基频分量法；电压增益；参数

中图分类号：TM131.4+1 文献标志码：A 文章编号：2095-2945（2017）23-0001-03

引言

移相全桥变换器在直流变换中应用广泛，但是存在次级二极管关断时反向恢复严重的特点[1]。所以，在中大功率DC/DC变换的应用中，全桥LLC谐振变换器以能在宽输入全负载范围内实现原边开关管的零电压开通和副边整流二极管的零电流关断，降低了开关损耗，而且变压器的漏感可作为谐振电感，减小了变换器的体积等优点，成为当前谐振变换器[2]的研究热点。文章详细分析了通态状态下全桥LLC谐振变换器的工作状态，并运用基频分量法[3][4]对其进行稳态建模，详细讨论了电压增益和谐振网络参数对全桥LLC谐振变换器的影响。

1 全桥LLC谐振变换器的工作原理和主要波形

全桥LLC谐振变换器拓扑结构如图1所示，图中，Q1-Q4为主功率开关管，D1-D4，C1-C4为开关管的体二极管与寄生电容，T为主功率变压器，DR1和DR2为输出整流二极管，谐振电感Lr，谐振电容Cr和励磁电感Lm组成LLC谐振变换器的谐振网络。

LLC谐振变换器电路有两个谐振频率，一个是谐振电感Lr和谐振电容Cr的谐振频率fr，另一个是Lm和Lr，Cr形成的谐振频率fm。即

选取不同的全桥LLC谐振变换器开关频率f，则有三种工作模式，即f>fr，fm

阶段1（t0-t1）：在t=t0时刻之前，Q1，Q3的寄生反并联二极管D1，D3已经导通，因此，在t=t0时刻，Q1，Q3实现零电压开通。变压器原边承受正向电压，整流二极管DR1导通，为负载提供能量，DR2截止。此时励磁电感的电压被钳位在nV0，不参与谐振过程，励磁电流im线性上升。

阶段2（t1-t2）：在 t=t1时刻，谐振电流ir与励磁电流im相等，整流二极管DR1零电流关断，输出侧与谐振回路完全脱离，DR1和DR2的电流为零，励磁电感Lm不在被钳位，参与谐振过程，谐振电流 ir继续对谐振电容Cr充电。

阶段3（t2-t3）：在t=t2时刻，开关管Q1、Q3关断，谐振电流ir对Q1、Q3的结电容充电，Q2、Q4的结电容放电，在t3时刻，Q2，Q4两端电压下降到零，为Q2，Q4零电压开通准备了条件。

阶段4（t3-t4）：开关管 Q1、Q3 仍是关断状态，ir和im都在下降，变压器原边承受反向电压，整流二极管DR2导通。励磁电感的电压重新被输出钳位，所以，退出谐振过程，参与谐振的只有谐振电感 Lr和谐振电容Cr。

阶段5（t4-t5）：在t=t4时刻，開关管Q2，Q4开通，输入电压通过Lr，Cr谐振向负载传输能量。在t=t5时刻，谐振电流ir与达到励磁电流im相等，输出侧与谐振回路脱离，整流二极管 DR2 实现零电流关断，Lm仍被钳位，不参加谐振，励磁电流im线性下降。

阶段6（t5-t6）：在t=t5时刻，整流二极管DR2零电流关断，输出侧与谐振回路脱离，励磁电感的电压不在被钳位，参与谐振过程。

阶段7（t6-t7）：在t=t6时刻，开关管Q2、Q4关断，Q1、Q3结电容放电。在t=t7时刻，寄生二极管D1、D3 导通，Q1、Q3两端的电压下降到零，为开关管 Q1、Q3 的零电压开通准备了条件。

阶段8（t7-t8）：开关管 Q2、Q4 仍然关断，整流二极管DR1导通。励磁电感的电压被输出钳位，所以，不参与谐振过程，发生谐振的只有谐振电感 Lr和谐振电容Cr。

2 基频分量法对全桥LLC谐振变换器建模

基频分量法可以将非线性的谐振电路化成正弦交流电路，采用正弦稳态电路的分析方法，简化了分析和计算；另外，该方法能为实际工程提供切实可行的设计指导，并能清晰表达谐振变换器的稳态特性。

基频分量法[6][7][8]（First Harmonic Approximation），假定功率经过谐振网络从电源传输到负载，只与电压和电流的傅利叶展开式中的基频分量相关。这种特性是与谐振网络的选择特性是一致的。在做稳态分析前，先做以下假设：

（1）所用开关管、二极管、电感、电容和变压器均为理想元件；（2）开关管寄生电容不参与谐振，其影响可以忽略；（3）输出滤波电容足够大，故输出电压纹波很小，可近似认为是一个电压源；（4）忽略开关频率谐波，电路中各电量只考虑基波分量。

如图3为全桥LLC谐振变换器的网络划分，可以将其划分为：开关网络，谐振网络，整流滤波网络[9][10]。

2.1 开关网络的建立

开关管Q1，Q3和Q2，Q4交替互补导通，则a，b两端电压是以Vin为幅值的方波电压，Uab傅里叶变换得：

2.2 整流滤波网络的建立

由模态分析可知，谐振电流ir（t）可近似认为是正弦基波分量，其频率与开关频率相同，表达式为：

3 电压增益分析

由全桥LLC谐振变换器基频分量法的等效电路可求出谐振网络的传递函数为：

因为变压器的匝比是可以确定的，不考虑变压器匝比的情况下，以fn为自变量的增益分析。

（1）固定m不变，Q取不同的值。（m=0.2）

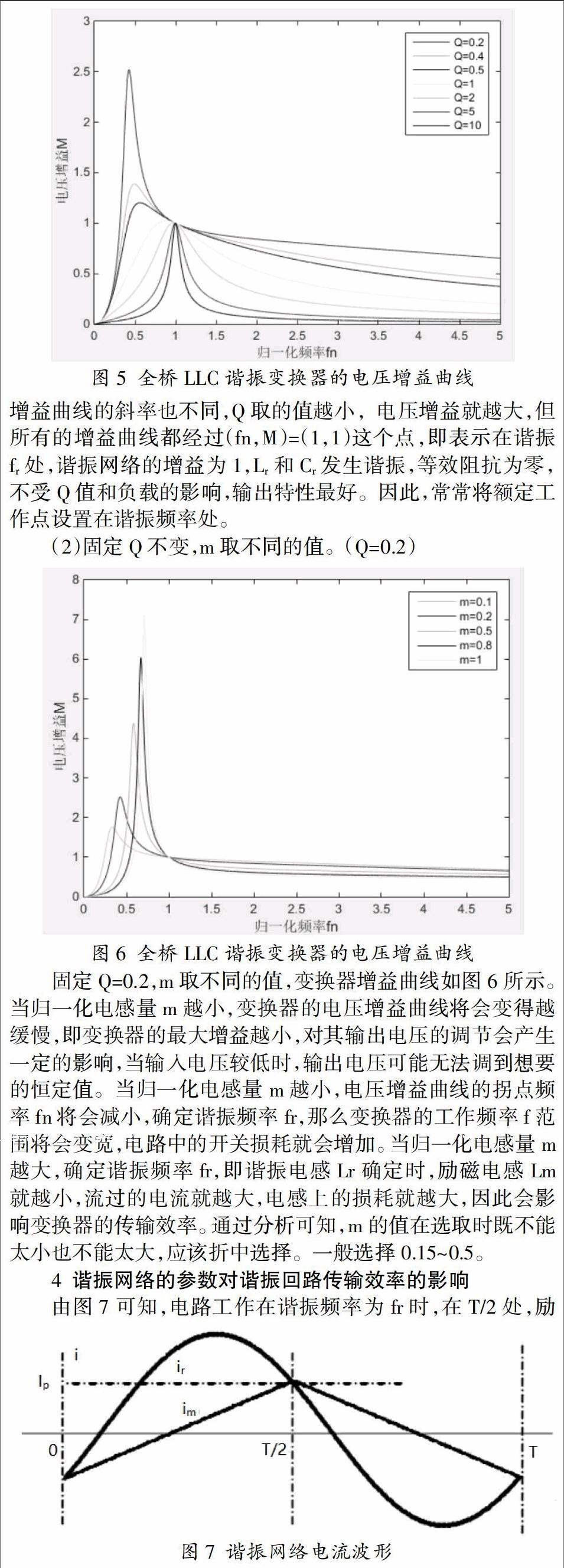
固定m=0.2，Q取不同的值，变换器增益曲线如图5所示。不同的Q值，其相应的增益曲线的斜率也不同，Q取的值越小，电压增益就越大，但所有的增益曲线都经过（fn，M）=（1，1）这个点，即表示在谐振fr处，谐振网络的增益为1，Lr和Cr发生谐振，等效阻抗为零，不受Q值和负载的影响，输出特性最好。因此，常常将额定工作点设置在谐振频率处。

（2）固定Q不变，m取不同的值。（Q=0.2）

固定Q=0.2，m取不同的值，变换器增益曲线如图6所示。当归一化电感量m越小，变换器的电压增益曲线将会变得越缓慢，即变换器的最大增益越小，对其输出电压的调节会产生一定的影响，当输入电压较低时，输出电压可能无法调到想要的恒定值。当归一化电感量m越小，电压增益曲线的拐点频率fn将会减小，确定谐振频率fr，那么变换器的工作频率f范围将会变宽，电路中的开关损耗就会增加。当归一化电感量m越大，确定谐振频率fr，即谐振电感Lr确定时，励磁电感Lm就越小，流过的电流就越大，电感上的损耗就越大，因此会影响变换器的传输效率。通过分析可知，m的值在选取时既不能太小也不能太大，应该折中选择。一般选择0.15～0.5。

4 谐振网络的参数对谐振回路传输效率的影响

由图7可知，电路工作在谐振频率为fr时，在T/2处，励磁电流im与谐振电流ir相等，并达到最大值。

以上分析可知，当变换器的T和R确定，原边和副边谐振电流有效值都取决于励磁电感的大小。因此，变换器的传输损耗主要有励磁电感决定，而不是谐振电感和谐振电容，励磁电感的选择变得尤为重要。

5 结束语

本文分析了全桥LLC谐振变换器的原理，运用基频分量法建模和绘出的增益曲线详细分析了电压增益，以及谐振网络参数对谐振回路传输效率所产生的影响。结果分析表明，为了提高电压增益，Q和m应根据设计需要选择恰当的值，为减小变换器的传输损耗，励磁电感Lm应尽可能选取较大的值。

参考文献：

[1]陈军艳.大功率DC/DC模块电源的研究[D].江苏：南京航空航天大学，2004.

[2]B Lu，W Liu， Y Liang，et al.Optiomal Design Methodology for LLC Resonant Converter[A].Twenty-first Annual IEEE Applied Power Electronics Conference and Exposition，2006（APEC'06）[C].Dallas，2006：533-538.

[3]Erickson，Robert W.Fundamentals of Power Electronics[J].Second Edition.Kluwer Academic Publishers，2000.

[4]V.Vorperian and S.Cuk.Small-signal Analysis of Resonant Converter[J].IEEE Power Electronics Specialists，Conf.Rec.1983，269-282.

[5]文美娟.全橋LLC谐振变换器研究[D].陕西：西安科技大学，2013：25-29.

[6]Erickson，Robert W.Fundamentals of Power Electronics[J].Second Edition.Kluwer Academic Publishers，2000.

[7]V.Vorperian and S.Cuk.Small-signal Analysis of Resonant Converter[J].IEEE Power Electronics Specialists，Conf.Rec.1983：269-282.

[8]Erickson R W，Maksimovic D. Fundamentals of power electronics. 2nd Edition， Publisher： Kluwer Academic Publishers， 2001.

[9]刘大庆.LLC谐振型开关变换器特性及其参数优化设计方法研究[D].解放军信息工程大学，2010，41.

[10]Lin I L， Lin C W. Design Criteria for Resonant Tank of LLC DC-DC Resonant converter. IEEE Transactions on Power Electronics. 2010：427-432.