基于数据挖掘的信用评估研究
2017-09-01王哲元
邱 梅,王哲元
(1.南京邮电大学 计算机学院,江苏 南京 210003;2.福州大学 数学与计算机科学学院,福建 福州 350116)
基于数据挖掘的信用评估研究
邱 梅1,王哲元2
(1.南京邮电大学 计算机学院,江苏 南京 210003;2.福州大学 数学与计算机科学学院,福建 福州 350116)
信用如今已经渗透至社会生活、工作之中,信用评估是金融、通讯等服务行业对消费者个体的重要需求。在分析个人信用影响因素及其相关数据建模基础上,改进了应用Logistic回归建模过程中所用到的最速下降法,有效减少了回归建模过程中的迭代次数与迭代时间。原始最速下降法相邻方向是正交的,导致越是靠近极值点步长越小,收敛速度慢;而改进后的最速下降法通过结合上一次的搜索方向确定当前搜索方向,改变了原本锯齿形的曲折搜索路径。为验证所提出方法的有效性和可行性,围绕迭代次数与迭代时间进行了实验验证。验证实验结果表明,改进的最速下降法减少了计算过程中的迭代次数,从而提高了运算效率;针对影响信用数据提供不全的记录,将转移概率矩阵应用于信用评估,可解决未来信用预测评估问题。
信用评估;最速下降法;Logistic回归;转移概率
0 引 言
人们在每天的生活中都无时无刻产生着大量的数据,例如在进行行程安排或工作中。而这些数据都蕴含着信息,从这些信息中,可以对一些还未发生的不确定行为进行预测,或是结合已知的信息进行推测得到另外有价值的信息。例如,超市的购物清单就可能反映出商品之间的潜在关联性,即消费者在购买一个商品时可能会顺带购买另外某一件商品。对于经营者来说,这就是一条有价值的信息,其可以对商品布局提供一个参考,使得销售一件商品的同时可以提高另一件商品的销量。
随着互联网金融的发展,基于大数据的信用评估越来越受到关注。信用关乎着社会与经济的发展,银行可以依据个人或企业的信用度判断是否给予贷款以及信用卡业务,并且制定出具体适合的借贷协议,尤其是农户型小额贷款,评估参考指标不足,导致农户小额贷款融资难的现状[1]。
信用度取决于很多方面,包括年龄、年收入、存款等等。而具体某一项和信用的相关度都是不等的,计算判断某个随机个体的信用度过程就是当前研究的主要内容,此外还尝试对具体信用样本未来可能的变化进行预测,以帮助解决由于信用度不够当下难以获得金融服务的群体的问题,同时降低其借贷成本。
1 信用评估指标
对用户的信用进行评估,选取影响信用的因素是至关重要的,考虑因素不全面则评估结果会产生偏差。从家庭状况、偿还能力、信誉状况、经营状况、经济环境五个方面进行考虑[2-3]。
1.1 家庭状况
家庭状况主要包括户主的年龄、劳动力的数量、劳动力的受教育程度、劳动力的健康状况、家庭的婚姻状况、家庭的负担状况、家庭成员的职业类型、家庭成员的职业职位、成员的户口性质、成员的对外连带责任担保状况等[4]。
1.2 偿还能力
偿还能力主要指家庭的年纯收入、家庭总财产、借贷款情况、家庭支出状况以及获取社会资源能力。
1.3 信誉状况
信誉状况主要包括不良记录情况、惩罚情况、还款情况、是否为老客户以及面谈印象。
1.4 经济环境
经济环境主要包括地区经济发展程度、发展稳定性以及政府优惠政策。
1.5 数据处理
数据分为两种,一种是定性类型,如受教育程度,可以分为五种量级,包括初中及以下、高中、大专、科、硕士及以上。通过打分制,最高的为5分,最低的为1分。还有一种情况,如户口性质,只有农村户口与城市户口之分,则指标值为1和0。另一种是定量类型,如家庭收入等等。
2 数据挖掘应用
现有的信用评估体系仅仅覆盖了大部分享受过金融服务的群体,而无法覆盖信用记录不完整或不够完善的消费者。比如刚毕业进入职场的青年或是还未涉足商场的创业者,又或者是远离大都市的农户想要在农业方面进一步扩展需要资金的情况,其共同点是无法获得常规的金融服务,或是要付出很大的代价才能获得基本的金融服务。现有的信用评估模型的基本思想是将数据库中全体借款人的信用背景信息进行建模,然后将待检查的借款人的历史资料及个人信息带入该模型,得出该借款人的信用度。还有的方案则是将信用度高的和经常违约、随意透支等各种陷入财务困境的借款人的群体分别建模,然后比较该借款人与哪个模型的距离更近,从而判断该借款人的信用情况。
2.1 模型的建立
根据上一节对影响信用的因素的分析,将已收集到的指标数据进行建模。运用分类算法,将数据分类成信用度高的群体和信用度低的群体。若y代表信用度的高低,针对数据特征可以选用线性回归,选取0.5为临界点,右侧为y=1,左侧为y=0。图1为线性分类图。

图1 线性分类图
对于信用评估,通过对已获得的数据建立一个模型,即用一条线去拟合这些数据,然后将待预测的样本数据带入到该模型中,获得返回值,即新样本的信用预测结果。这里采用线性回归来构建模型。假设用x1,x2,…,xn描述特征变量,可以构造出一个估计函数:
h(x)=hθ(x)=θ0+θ1x1+…+θnxn
(1)
其中,θ表示特征变量的参数。定义x0=1,则公式可表示为:
(2)
其中,n表示特征数目。
使式(2)尽可能地拟合数据,需选取合适的参数θ,可以用损失函数来描述h(x)的拟合程度,如下:
(3)
通过改变θ使该损失函数值尽可能小,当函数值收敛于0,选取此时θT,模型建成。调整θ使J(θ)取最小值的方法有很多,包括最小二乘法、最速下降法等方法。
2.2 最小二乘法
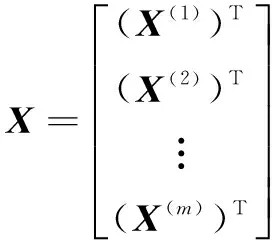
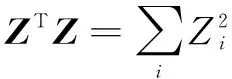
(4)
对θ求导,化简得:
(5)
但是,计算一个矩阵的逆是相当耗时的,而且求逆也会存在数值不稳定的情况,最速下降法相比较而言计算量不是特别大,收敛性有保证,只是迭代次数可能较高[5]。
2.3 最速下降法
最速下降法是沿负梯度方向,函数下降最快,由J(θ)对θ的偏导数确定,如下:
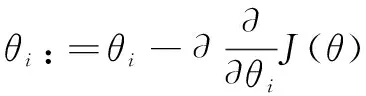
(6)

θi:=θi-∂(hθ(x)-y)·xi
(7)
如此迭代更新,最终确定θ。
为了导出梯度下降的方向,需要关于每个参数的分量对目标函数求偏导[6]。
(8)
则梯度下降的规则是:
(9)
2.4 改进的最速下降法
最速下降法具有很好的整体收敛性,但在相继两次迭代中,方向是相互正交的,则在逼近极值点的路线是锯齿形的,并且越靠近极值点步长越小,即越走越慢[7]。
为了解决最速下降法收敛速度在逼近极值点缓慢的问题,提出了SDM Imp(Steepest Descent Method Improved),具体描述如下:
假设在二维图形中,此时可以考虑在接近极值点时,选取xk-1和xk的方向和作为xk的方向,这样能获得更快的收敛速度,从而提高算法效率,拟合原本模型的方向,如图2所示。
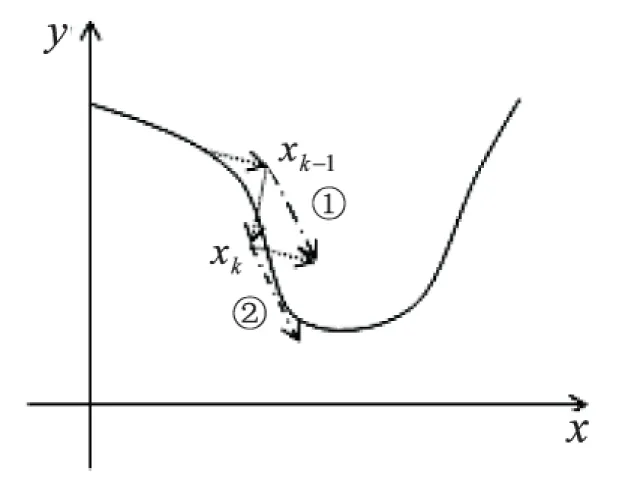
图2 最速下降法的改进图例
2.5 Logistic回归

Logistic回归方程为:
(10)
转换得:
(11)
对假设进行概率上的解释,有:
p(y=1|x;θ)=hθ(x)
(12)
p(y=0|x;θ)=1-hθ(x)
(13)
结合有:
p(y|x;θ)=hθ(x)y(1-hθ(x))1-y
(14)
数据的概率即参数的似然性为:

(15)
则问题转化为找到参数θ的一个极大似然估计[11],即需要找到参数θ使得似然性L(θ)最大化,推导时,使似然性的对数最大化比使似然性最大化容易得多,则对上式两边求对数得:
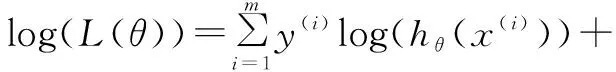
(16)
则问题转化为求对数最大化的最优化问题,可采用改进后的最速下降法。
2.6 一步转移概率矩阵的应用
上述对信用估计模型的构建,确定了每个特征变量前面的参数θ,每个特征对结果的影响强弱可由前面的参数体现,能够实现对当前新样本数据进行信用评估,但是这还不能体现目前信用度不高的群体未来的信用情况,所以该模型不能适用于目前信用度不高但未来很有潜力的群体,预测他们是否可以享受到基本的金融服务[12]。针对这样的情况,结合马尔可夫过程,设计了应用一步转移概率的解决方案,根据概率转移矩阵,就能得到状态之间经过一步或多步转移的规律,从而实现根据当下的初始状态对后期进行预测[13]。其具体步骤为:
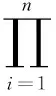
(2)计算出经某一段时间T从某个状态转移至另一个状态的概率,即构造出一步转移概率矩阵Zt×t。
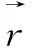
(5)将各状态带入之前求得的模型,得到该用户的信用结果。
假设时间段T为一年,一步转移概率矩阵Zt×t,每个元素代表了个体从某个状态经过一年可能成为其他各个可能状态的概率。例如,若现只考虑两个指标—学历与年收入,学历分为4个状态,包括初中及以下、高中或大专、本科、硕士及以上,年收入分为5个状态,包括2万及以下、2万~5万、5万~10万、10万~20万、20万及以上,则总共存在20个状态,包括学历为初中及以下且年收入为2万以下,学历为初中及以下且年收入为2万~5万,等等。设计矩阵Z20*20,其中Zij=p(j|i)表示在当前状态i下一时间段会转成状态j的概率。将当前状态的初始向量乘上该矩阵,就可以得到该初始状态的个体在下一年可能转变成的状态情况。

(17)
然后计算出非零状态下的信用结果,求出该向量对应的信用,即
f(x)=ft
(18)
其中,ft为向量中非零元素对应的第t个状态下的信用,则可以实现对下一年信用的预测。

(19)
其中,l为向量中非零元素的个数;ft为第t个状态下的信用[14]。
如此将一步状态转移矩阵运用到对信用的预测中,还可以预测a年后该样本可能的所处状态。
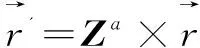
(20)
然后结合各状态的信用,计算出未来的信用度,这更能符合提供金融服务的机构对客户信用度的需求。例如,借贷服务、金融服务机构需要考虑的是客户在还贷期间的信用情况,相比于当下的信用度可能更具参考价值。
3 实验结果与分析
综上可知,最速下降法的相邻搜索方向是正交的,改进后的方法通过改变方向更快速地逼近极值点,所以为了测试改进后的方法,就将改进前后的方法应用于计算的迭代次数与运行时间进行比较。
一方面,在相同的数据个数及实验次数下,比较两种方法计算过程中的迭代次数,结果如图3所示。

图3 改进前后的迭代次数对比
另一方面,在相同的数据个数及实验次数下,比较两种方法计算过程的耗费时间,结果如图4所示。
从上述实验结果可以看出,改进的最速下降法性能上比原始方法要好,运算效率有所提高。
4 结束语
针对信用评估问题,对已有的影响信用数据进行处理与建模,提出了一种最速下降法的改进方法,能够在建模过程中更高效地运算。另外,将一步转移概率应用到信用的评估预测中,实现了对影响信用数据不足的用户所进行的评估以及对未来一段时间后的用户信用所进行的评估。

图4 改进前后的运算时间对比
[1] 陈永明,周 龙,李双红.基于AHP和DEMATEL方法的农户信用评级研究[J].征信,2012(5):20-24.
[2] 孙玲芳,祁 军,徐 会,等.面向交易型虚拟社区的信用评价模型研究[J].信息技术,2014,38(7):74-77.
[3] Lu Jianchang,Wu Jipeng.The fuzzy comprehensive evaluation on credit risk of power customers based on AHP[C]//Second international symposium on information science and engineering.Shanghai:[s.n.],2009:148-151.
[4] 李俊丽.基于层次分析法的农户信用评估[J].商业研究,2009(10):125-127.
[5] Qiu Y. An importance sampling method based on variance minimization with applications to credit risk[C]//Proceedings of the 29th Chinese control conference.Beijing:[s.n.],2010:3176-3179.
[6] 吴 锋,李秀梅,朱旭辉,等.最速下降法的若干重要改进[J].广西大学学报:自然科学版,2010,35(4):596-600.
[7] 李鸿仪.理想化最速下降法及其逼近实例[J].上海第二工业大学学报,2011,28(1):8-13.
[8] 池光辉,刘建伟,李卫民,等.权核Logistic回归模型的分类和特征选择算法[J].计算机工程与应用,2013,49(9):41-44.
[9] 王 鹏,孙继银,郭文普,等.前视红外目标匹配中的图像质量建模[J].计算机应用研究,2012,29(12):4797-4800.
[10] 郑兰祥,万 雪.基于Logit法的我国农村小额贷款公司信用风险评分模型构建研究[J].安徽农业大学学报:社会科学版,2014,23(4):49-54.
[11] 姜 盛.基于Logistic的信用卡套现侦测评分模型[J].计算机应用,2009,29(11):3088-3091.
[12] Mastin A,Jaillet P.Loss bounds for uncertain transition probabilities in Markov decision processes[C]//51st IEEE conference on decision and control.Maui,HI:IEEE,2012:6708-6715.
[13] 冯学伟,王东霞,黄敏桓,等.一种基于马尔可夫性质的因果知识挖掘方法[J].计算机研究与发展,2014,51(11):2493-2504.
[14] Hu Yuting,Xie Rong,Zhang Wenjun,et al.Prediction of tourists flow distribution based on transition probability matrix[C]//8th international conference on information science and digital content technology.Jeju Island,Korea:[s.n.],2012:636-640.
Investigation on Credit Evaluation Based on Data Mining
QIU Mei1,WANG Zhe-yuan2
(1.College of Computer,Nanjing University of Posts and Telecommunications,Nanjing 210003,China;2.College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350116,China)
Credit has been combined closely with people’s daily life and work.And credit assessment maintains a significant requirement of customers in service industries such as finances and communications.In this paper,the Steepest Descent Method (SDM) in Logistic Regression analysis has been improved based on influence factors of credit and relative data of modeling,reducing iteration times and time in regression modeling.The strategy can be explained that in original SDM,adjacent searching directions keep orthogonal and steps approach zero when they are close to the extreme point,which contributes to a slow rate of convergence.Yet,in the improved scheme,current searching direction has been determined by the last one and zigzag directions are eliminated therefore.In the experiments,it is proved that times of iterations is decreased and computational efficiency is enhanced.Moreover,aiming at defective credit records,matrix of transition probability has been adopted in order to solve problem of the credit assessment and prediction in the future.
credit evaluation;steepest descent method;Logistic Regression;transition probability
2016-08-02
2016-11-10 网络出版时间:2017-06-05
国家“863”高技术发展计划项目(2006AA01Z201)
邱 梅(1992-),女,硕士研究生,研究方向为数据挖掘、机器学习。
http://kns.cnki.net/kcms/detail/61.1450.TP.20170605.1507.048.html
TP311
A
1673-629X(2017)08-0047-05
10.3969/j.issn.1673-629X.2017.08.010
