基于能量机制的多头绒泡菌动力学优化算法
2017-08-31虞慧群
刘 阳 冯 翔,2 虞慧群 罗 飞
1(华东理工大学信息科学与工程学院 上海 200237) 2 (上海交通大学智慧城市协同创新中心 上海 200240) (18255387158@163.com)
基于能量机制的多头绒泡菌动力学优化算法
刘 阳1冯 翔1,2虞慧群1罗 飞1
1(华东理工大学信息科学与工程学院 上海 200237)2(上海交通大学智慧城市协同创新中心 上海 200240) (18255387158@163.com)
随着人工智能和大数据的迅猛发展,大数据的爆炸式增长和问题的复杂性分布导致对并行智能处理的要求日趋迫切.传统的理论模型和技术方法面临严峻挑战,受自然界启发的物理学法则和生物学方法逐渐成为研究热点.受多头绒泡菌的生长觅食等行为启发,提出了一种基于能量机制的多头绒泡菌动力学算法(physarum-energy dynamic optimization algorithm, PEO).该算法以多头绒泡菌算法为基础,根据其动力学特征,引入能量机制,以改进现有的多头绒泡菌算法全局信息交互能力差等缺点.此外,PEO引入了年龄因子的概念和扰动机制,以控制算法在不同阶段的寻优能力和收敛速度,并从理论角度对算法模型的收敛性进行证明.最后,通过在TSP数据集上实验证明算法在不同规模数据集的有效性和收敛性,并进行了参数分析.与其他的优化算法的对比实验数据表明,PEO在面对复杂问题的求解速度和收敛速度明显优于其他的优化算法,具有高精度和快收敛的特性.
多头绒泡菌动力学优化算法;能量机制;年龄因子;旅行商问题
正如微软的创始人之一Allen在《Science》上发表的论文“New frontiers in bioscience”中所说:“探索生物学的复杂性是一场迷人的挑战,我渴望能探索它的奥义与阵地,建立出可靠的预测模型并将其应用于实际中去.这种极富创新性和创造性的工作极大地推动了人类社会的进步,也正是这种信念支持着我对基础科学的不懈研究[1].”随着信息科学技术的迅猛发展,研究者们受自然规律或生物行为的灵感启发,提出了许多有效成熟的理论模型和算法思想,并得到了广泛的应用[2-4].其中自然行为[5]、群体行为[6]、生物行为[7]等,这些算法已经广泛地应用于生活的各个方面,并能成功地解决各种复杂的问题.
著名的旅行商问题(traveling salesman problem, TSP)是组合优化问题领域中最重要和最有代表性的问题之一,在过去的半个世纪以来,吸引了大量的研究人员为此不懈努力.TSP是一个典型的NP难题,其搜索空间巨大,即在多项式时间内无法精确求解.当前对于TSP问题的应用主要包含印刷电路板的制造、车辆路由和调度问题等.针对该类问题,目前主要有2种方法求解,精确的传统方法和高效的智能算法.由于TSP问题的时间复杂度呈指数级增长,精确的传统方法例如动态规划法,只能解决规模较小的简单问题.当面临大规模的复杂问题时,该类方法失效.为了可以在合理的时间空间代价下有效地解决大规模TSP问题,就有必要提出能够寻找次优解的智能算法.智能算法虽然不一定能够精确的求解问题,但是对于规模较大的问题,可以在有限时间内将解的有效性控制在一定的误差范围内.
迄今为止,现有的求解TSP问题的智能算法主要有弹性网络算法[8]、基于蚂蚁行为启发的蚁群算法[9-10]、鸟群群内觅食行为的粒子群算法[11]、基于演化策略的遗传算法[12]、源于热力学中退火原理的模拟退火算法[13]等.对于现有的智能算法来说,虽然能够在有限时间内找到问题的近似最优解,但是依然存在各种不足有待继续优化改进.其中,弹性网络算法虽然具有较好的并行性,但是依然存在局部最小值和参数调整问题[14];蚁群算法虽然求解精度较高,正反馈机制且参数较少,但计算时间长,收敛速度慢[15];粒子群算法具有强大的全局搜索能力,但是极易陷入局部最优[16];遗传算法简单,具有快速搜索能力,但在计算演化过程中易早熟收敛,交互信息能力差,计算代价大[17];模拟退火算法具有较强的局部优化能力,但缺乏对搜索空间的了解,搜索过程不易趋向希望方向,求解效率低下[18]等.
随着启发式算法的深入研究发展,简单单一的经典算法模型通常就会具有很大的局限性.为了能弥补现有算法的不足,近年来研究人员也提出了许多改进算法,例如Arshad等人提出的混合GA算法[19]、Saadatmand-Tarzjan等人提出的构建优化神经网络算法[20]、Hu等人提出的可变采样蚁群优化算法[21]、Ye等人提出的改进的混合模拟退火遗传算法[18]等.然而,当待求解问题越发复杂,为了寻找更优的解决方案,经典算法的改进模型就会对复杂问题进行更为细致的刻画,即可能出现算法的可扩展性变差或者虽精度提高但求解速度降低等情况.
针对以上不足,需要提出更为有效的智能优化算法模型,该算法模型需要能够高度并行且收敛,有较好的全局寻优能力,在求解大规模复杂问题时既能够保证求解精度,又能提高寻优效率,在两者之间找到很好的制衡点,以满足待解决问题的需要.本文受多头绒泡菌生长觅食行为启发,根据其在演化行为过程中的能量变化及并行行为,提出基于能量机制的多头绒泡菌动力学优化算法(physarum-energy dynamic optimization algorithm, PEO),使得其在解决大规模的复杂问题中具有高度并行性和快速求解能力.此外,引入年龄因子机制,以控制算法在不同阶段的寻优能力和寻优精度,避免陷入早熟收敛.
本文的主要贡献有5个方面:
1) 提出基于能量机制的多头绒泡菌动力学优化算法PEO,在解决复杂问题中具有高度的并行性和全局寻优能力;
2) 基于动力学机制,设计能量函数,构建多头绒泡菌能量子模型,保证算法收敛;
3) 提出年龄因子模型,控制算法在不同阶段的寻优能力和寻优精度;
4) 引入随机扰动子模型,避免算法陷入早熟收敛;
5) 建立多头绒泡菌的生物物理模型和数学模型,并给出收敛性证明和理论可行性证明.
1 相关工作
2000年,Nakafaki等人在《Nature》中提出,多头绒泡菌可以有效地解决迷宫问题[22].多头绒泡菌能根据外界环境情况来调整生长结构,使得机体向着最有利于生存的方向生长[23-26].本文受多头绒泡菌的觅食行为及规律的启发[27-28],刻画出多头绒泡菌觅食的生物模型.多头绒泡菌由于其趋食性会导致食物源产生压力差[29],即产生势能,而维持机体生长会导致能量耗损,所以该系统具有动力学特征.
2013年,Mersch等人通过研究发现,蚂蚁受年龄因素影响会导致社会化分工演变[30],年轻蚂蚁在蚁巢内部从事护理工作,中年蚂蚁分布在蚁巢各处进行清理工作,老年蚂蚁在蚁巢外侧进行觅食工作,如图1所示:
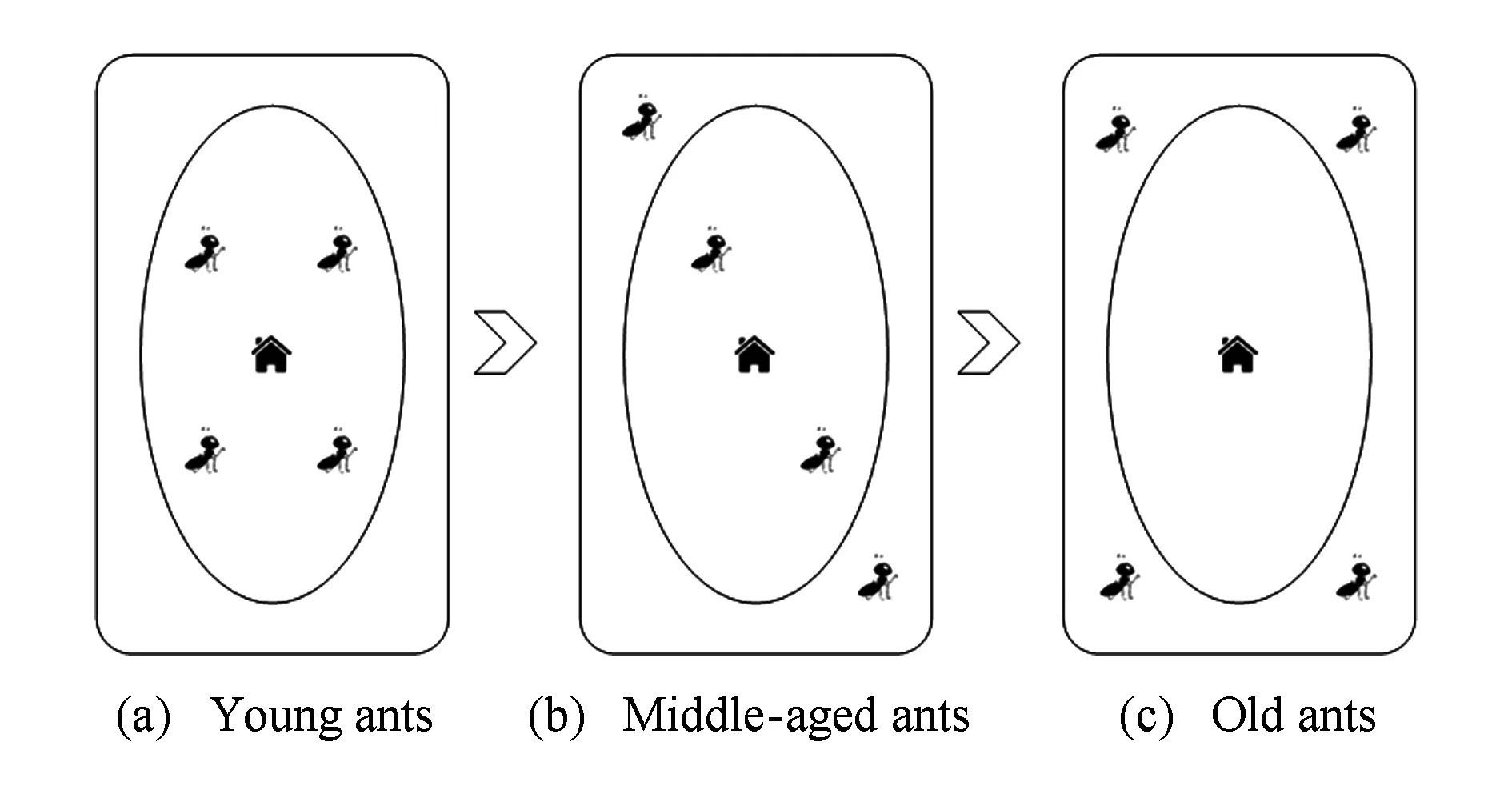
Fig. 1 Affection of ages to ants图1 蚂蚁受年龄因素影响示意图
2 问题描述
旅行商问题(TSP问题)是一个组合优化问题,也被证明了是NP难题,即:存在N个城市,旅行商由城市i出发,依次访问完所有的N个城市,并回到出发点i的最短路径长度.
对于TSP问题来说,需要访问城市的集合为:C={c1,c2,…,cn},城市ci的坐标为(xi,yi).假设旅行商访问的顺序集合为:Order={o1,o2,…,on},其中,oi表示旅行商访问顺序中第i个被访问城市的标号,1≤i≤n,on+1=o1,那么目标函数可以表示为
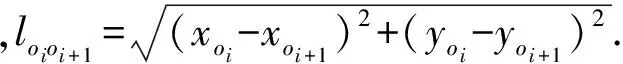
3 生物物理模型
3.1生物模型
定义1. 电导率.连接食物A和B管道内原生质流动的传导性被称为电导率.
定义2. 流量.连接食物A和B管道内单位时间内流动的原生质的体积被称为流量.
定义3. 压力.多头绒泡菌的趋食性导致食物对管道内原生质具有吸引力即压力.
定义4. 压力差.连接食物A和B管道内原生质的压力差值称为压力差.
由多头绒泡菌的觅食特性[26]可知,管道内原生质的流量和电导率存在着正反馈机制,如图2所示,即当管道内原生质的流量逐渐增多,管道电导率就会增大,电导率的增大又会进一步导致管道内流量增加,反之亦然.
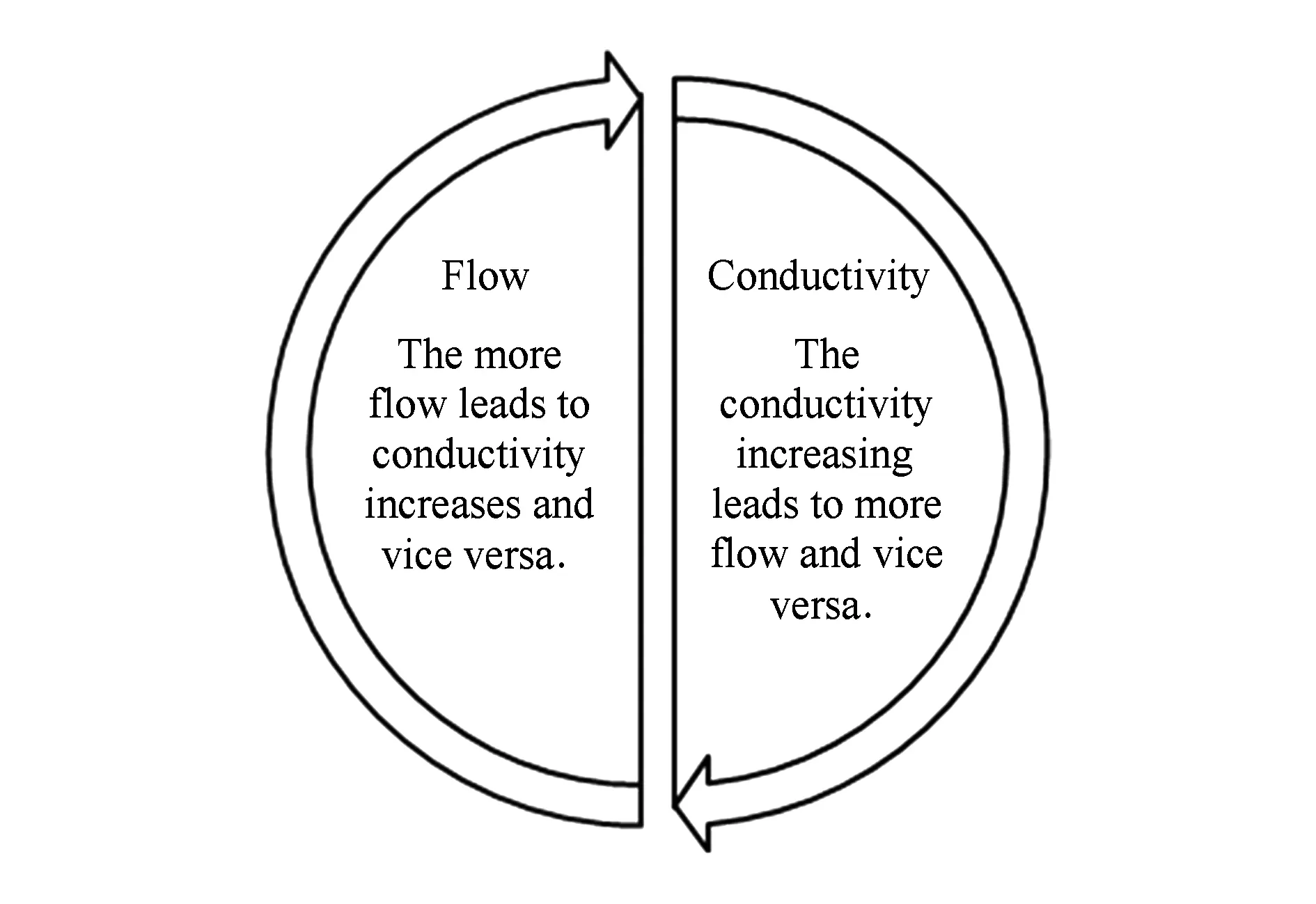
Fig. 2 Positive feedback mechanism of Physarum图2 多头绒泡菌机体的正反馈机制
3.2能量模型
多头绒泡菌体内的原生质在食物吸引力下流动,同时维持机体生长将导致能量耗损,即整个系统具有能量开销,因此多头绒泡菌具有着动力学特性[31].本文根据多头绒泡菌的动力学特性来构建能量模型.
连接食物源之间的原生质管道内存在着由压力差产生的势能,即原生质流动的动力.经过管道内流量和电导率间的正反馈机制不断演化,随时间的增长,流量和电导率逐渐趋于稳定.系统的能量变化也将逐渐趋于稳定.本文考虑整个系统中能量的变化受以下几种因素的影响.
定义5. 个体效用.连接食物A和B间管道的状态距稳定状态的差距,即该管道的成功值.该管道的成功值越大,其个体效用就越强.
定义6. 整体效用.所有的管道个体效用值的累加即整体效用.当系统达到最优解时,其整体效用将不再发生变化.
定义7. 目标吸引力.系统在演化过程中,以期望达到的最优状态对当前状态的吸引力.目标吸引力将会使个体效用最小的管道的效用值增加,以提高整体效用.
定义8. 交互信息行为.系统在演化过程中,各管道之间的变化相互影响的方式即交互信息行为.
能量模型在4种因素的影响下,向目标状态演化,这4种因素为:1)个体效用的优化行为;2)整体效用的优化行为;3)目标对整体的吸引力;4)个体管道结构之间的交互信息行为.
3.3年龄因子模型
PEO的整个演变过程按照其持续的时间长短可以划分为3个阶段,分别是初期的不稳定状态阶段、中期的亚稳定状态阶段以及后期的稳定状态阶段.
定义9. 不稳定状态.算法初期,系统的能量值、个体效用和整体效用变化幅度较大,算法趋向于全局寻优,收敛速度较快.
定义10. 亚稳定状态.算法中期,系统的能量值、个体效用及整体效用值变化幅度小于不稳定状态.该阶段算法的寻优能力更趋向于局部寻优,收敛速度较慢.
定义11. 稳定状态.算法后期至结束.系统能量值、个体效用值及整体效用稳定,算法已经求解到最优解.
年龄因子模型使得PEO在不同阶段选择不同的寻优机制,即不稳定状态时,提高全局寻优能力,加快收敛速度;亚稳定状态时,提高局部寻优能力,减缓收敛速度,以期在稳定状态时能够得到更理想的最优值.
3.4随机扰动模型
根据多头绒泡菌的避光性特点,随机光照扰动会对其生长结构产生一定影响.本文在PEO寻优过程中引入随机扰动机制.PEO算法的每次随机扰动将获得一个新解,如果新解的解质量优于当前解,则接受新解,否则将以一定概率接受新解,通过此机制使得算法跳出局部最优.
4 数学模型
4.1生物数学模型
首先对TSP问题中的主要变量进行描述,如表1所示:

Table 1 The Main Variables of TSP表1 TSP中的主要变量
定义12. 食物源i的位置坐标为(xi,yi).
定义13. 连接食物源i与j的管道长度是lij,即i点和j点之间的欧式距离:
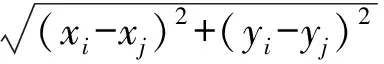
定义14. 连接食物源i和j的管道lij两端存在压力差pij,即点i的压力pi和点j的压力pj的差值的绝对值.
(1)
定义15. 连接食物源i和j的管道lij之间的流量用flowij来表示.根据哈根-泊肃叶方程得知:
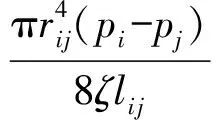
(2)
其中,lij是i和j之间的距离,rij代表管道的内径,ζ代表流体的粘度.
定义16. 连接食物源i和j的管道电导率用dij表示:
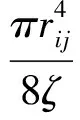
(3)
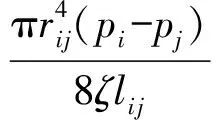
(4)
定义17. 电导率dij变化和流量flowij的关系为
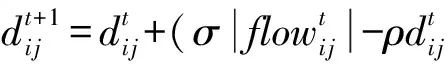
(5)
根据式(5)可得:
(6)
其中,机体维持管道会产生能量损耗,而σ和ρ是控制流量和能量耗损的权重系数.由此可见,管道内电导率的变化趋势和管道内流量的变化趋势是一致的,是正反馈作用的结果.
4.2能量数学模型
根据PEO的能量模型可知,其能量变化受4个方面的因素影响,以下对这4个因素进行数学模型构建:
定义18.uij(t)为食物源i和j之间管道的个体效用值,表示管道的连接状态距离目标值的径向距离,即距离目标的成功度.
(7)
其中,食物源i和j之间管道的距离lij越短,管内流量flowij越大,电导率dij也就越高.其向着目标的成功度也就越高,个体效用值就越强.
定义19.J(t)代表在时刻t的整个系统管道的整体效用,即:
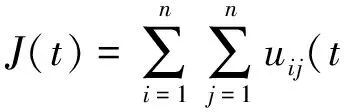
(8)
定义20. 管道之间的交互式行为函数Q(t):
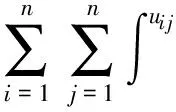
(9)
定义21. 在时刻t,由最终的目标产生的吸引力函数为
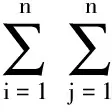
(10)
其中,0<ε<1,P(t)越大,即向着目标变化的速度越快,那么TSP问题的求解速度越快.
定义22. 系统在以上4个因素的影响下向目标结构演化的过程,通过混合的吸引力函数Eij(t)表示:
Eij(t)=-λ1uij(t)-λ2J(t)-λ3P(t)-λ4Q(t),
(11)
其中,0<λ1,λ2,λ3,λ4<1.
对于PEO来说,其比较显著的特点就是具有高度的并行性,对于管道的2个参数,电导率参数dij和压力差参数pij都可以动态并行地进行计算更新,从而可以达到高效快捷的求出目标优化解的目的,即:
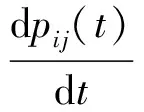
(12)
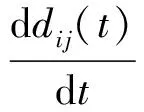
(13)
定义23. 个体效用随时间变化的变化率为
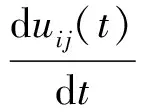
(14)
4.3年龄因子数学模型
算法的年龄因子将算法的阶段划分为3个阶段,第3个阶段算法已经取得了最优解,那么对算法的前2个阶段进行数学模型构建:
1) 初期的不稳定阶段
在初期的寻优搜索阶段,适当地加快算法的收敛速度.根据式(10)可知,参数ε的值控制着吸引力函数P(t)的大小.由此可以适当地增加ε的值,以提高算法收敛的速度,此时算法侧重全局寻优.
2) 中期的亚稳定阶段
在中期寻优阶段,适当地降低ε的值,以提高局部搜索的精度,适当降低算法的收敛速度.
4.4随机扰动数学模型
在PEO中引入扰动机制,即每次生长过程中,随机选择某管道,对其电导率dij在一定范围内添加扰动项,判断当前系统和扰动前系统的能量值变化,若能量增加,则以一定的概率接受当前的扰动修改,以提供一种防止算法陷入局部最优的机制.
定义24. 若能量增加,ΔE>0,接受当前修改的概率为
P(ΔE>0)=e-ΔEt,
(15)
其中,t为当前算法的迭代次数.
5 PEO算法
基于能量机制的多头绒泡菌优化算法PEO具体步骤为:1)初始化各个食物源的位置坐标,并且确定机体管道结构的电导率,压力差以及相关参数等;2)分别求得每个管道个体效用、整体效用、目标吸引力和交互信息等;3)不断迭代更新个体效用,并判断算法所处阶段,引入扰动机制;4)当个体效用不再发生变化时,算法结束,求得最优解.算法的主要流程如图3所示:
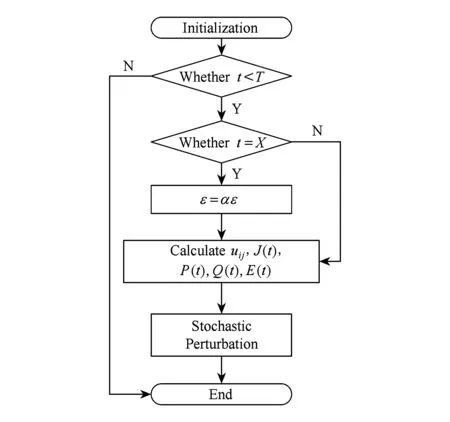
Fig. 3 The flow chart of algorithm图3 算法流程图
算法1. 基于能量机制的多头绒泡菌动力学算法
① 初始化所有点的坐标,获得各城市间的距离;
② 初始化所有边的电导率dij,压力差pij;
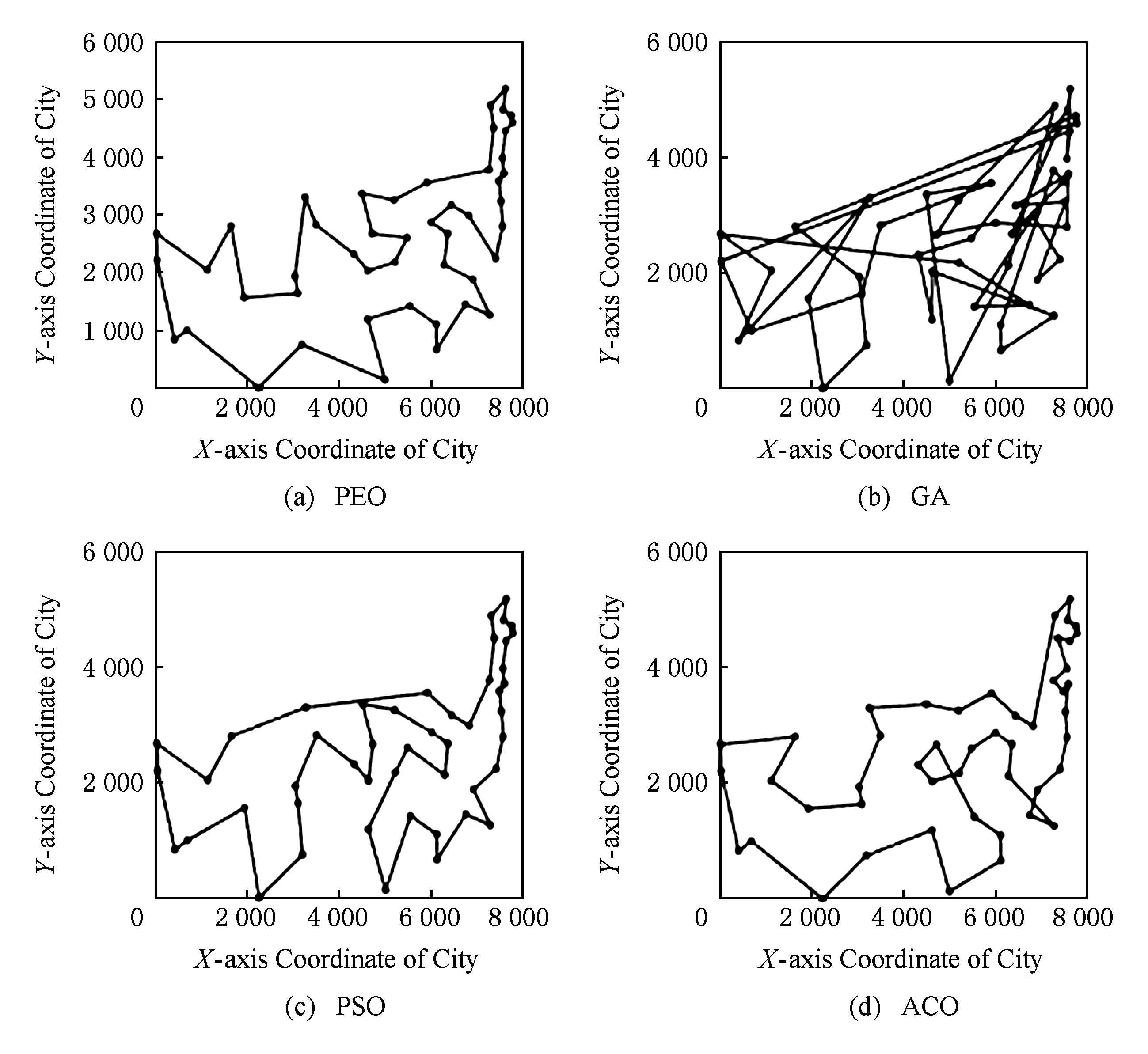
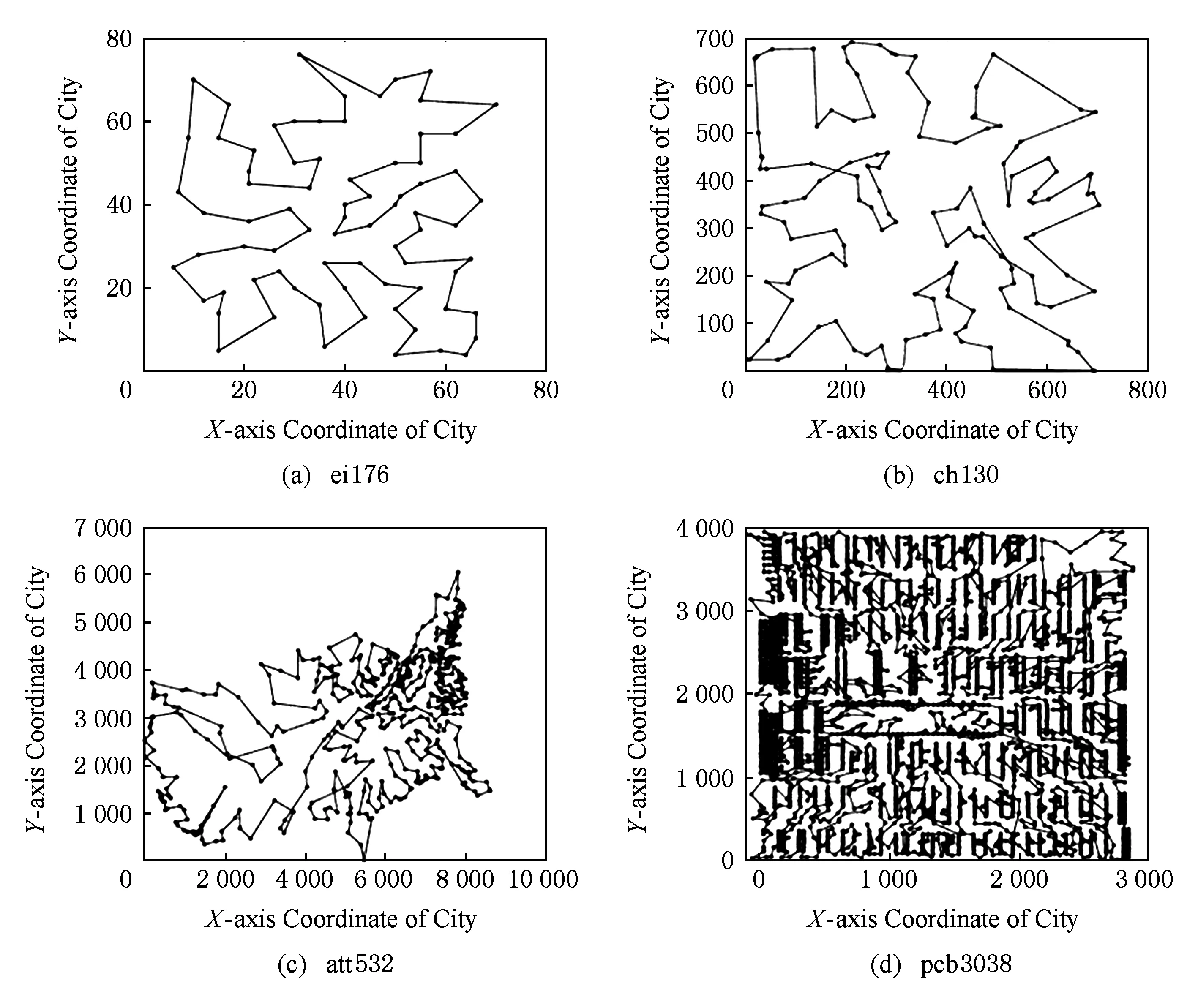
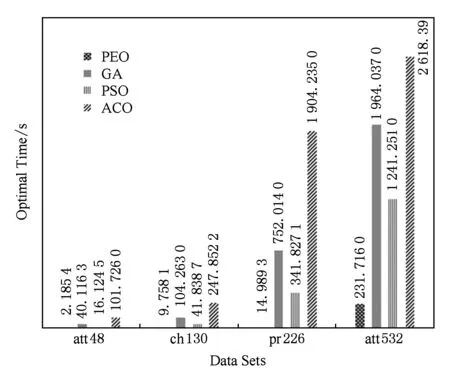
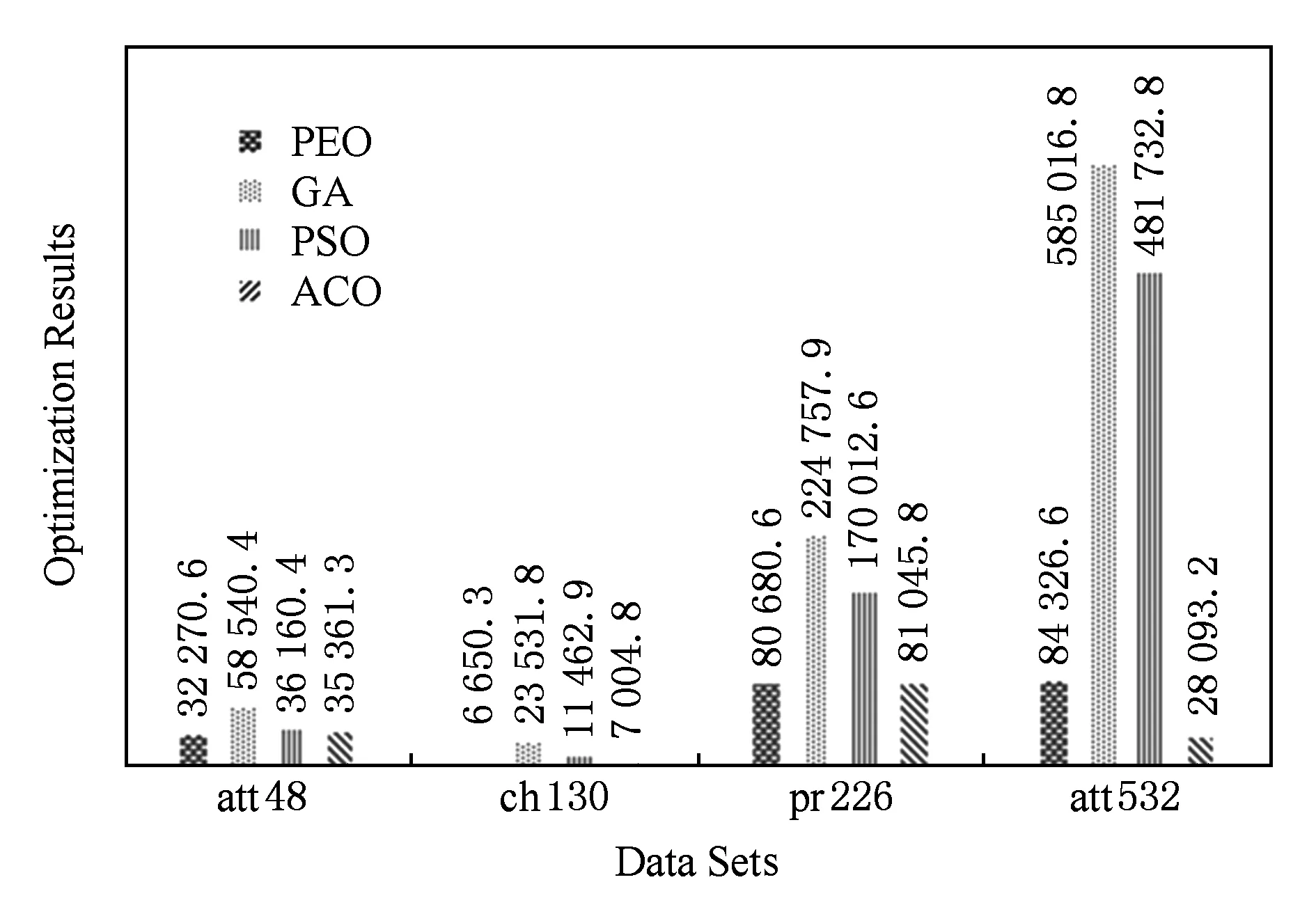
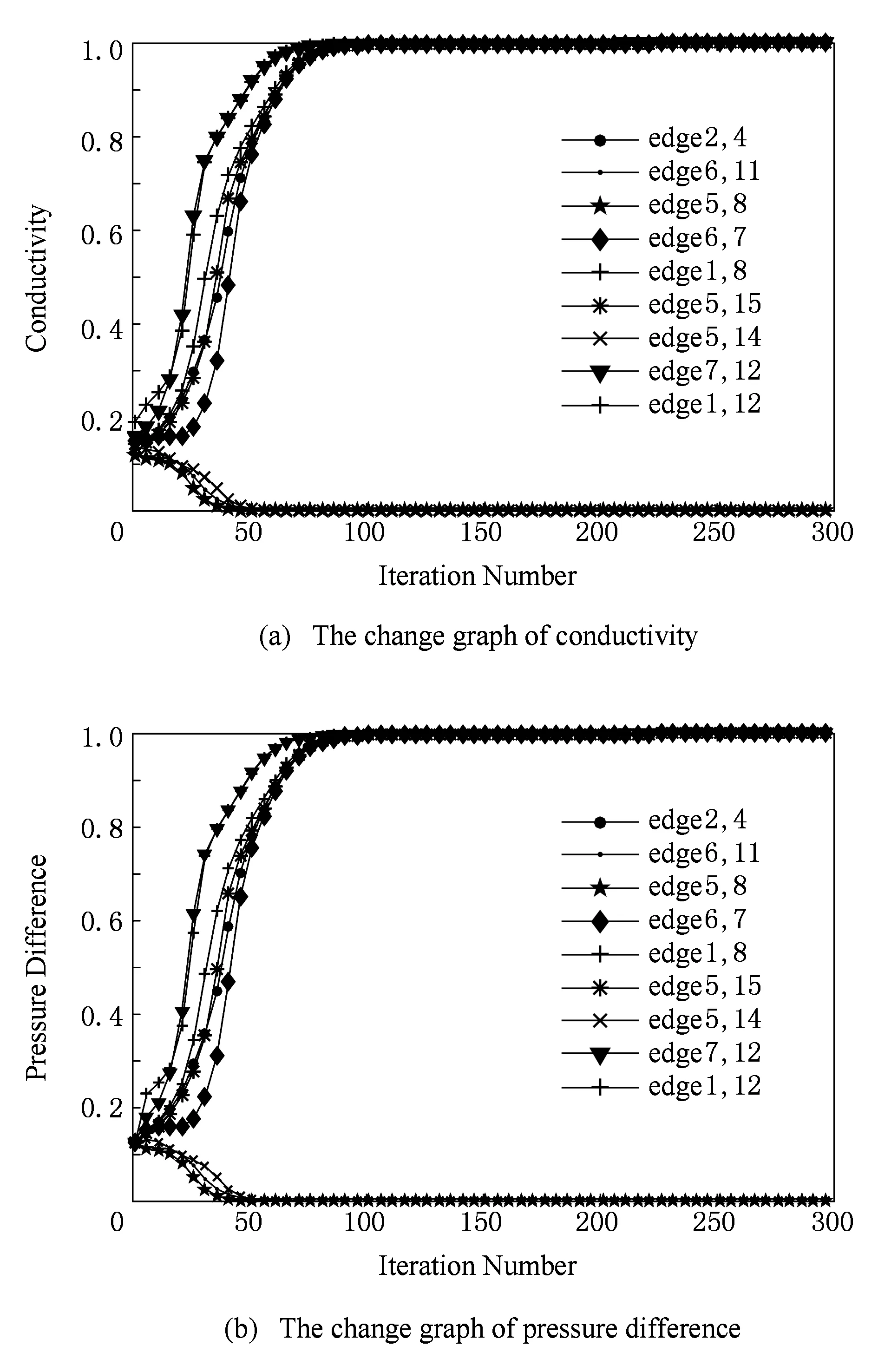
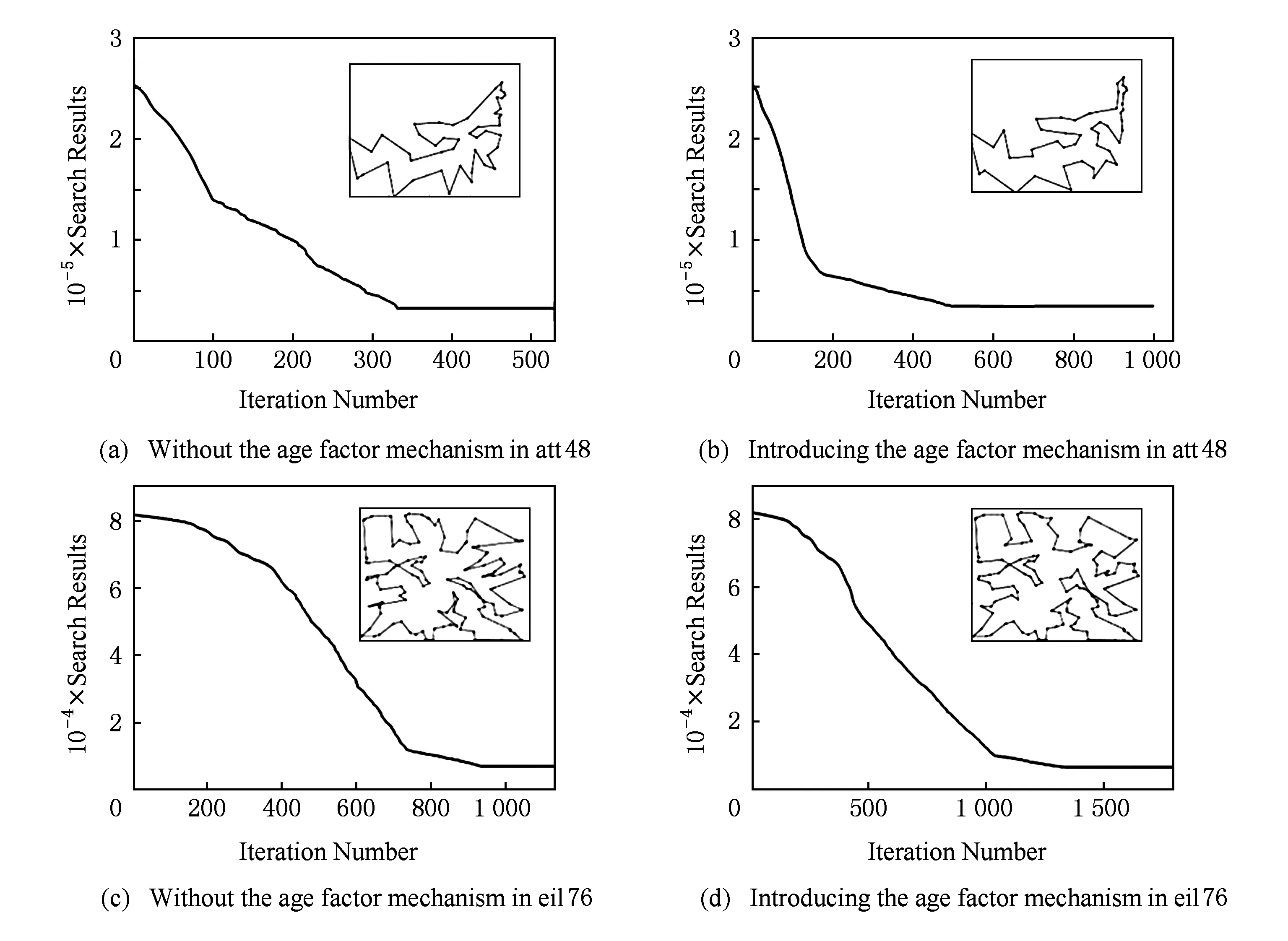
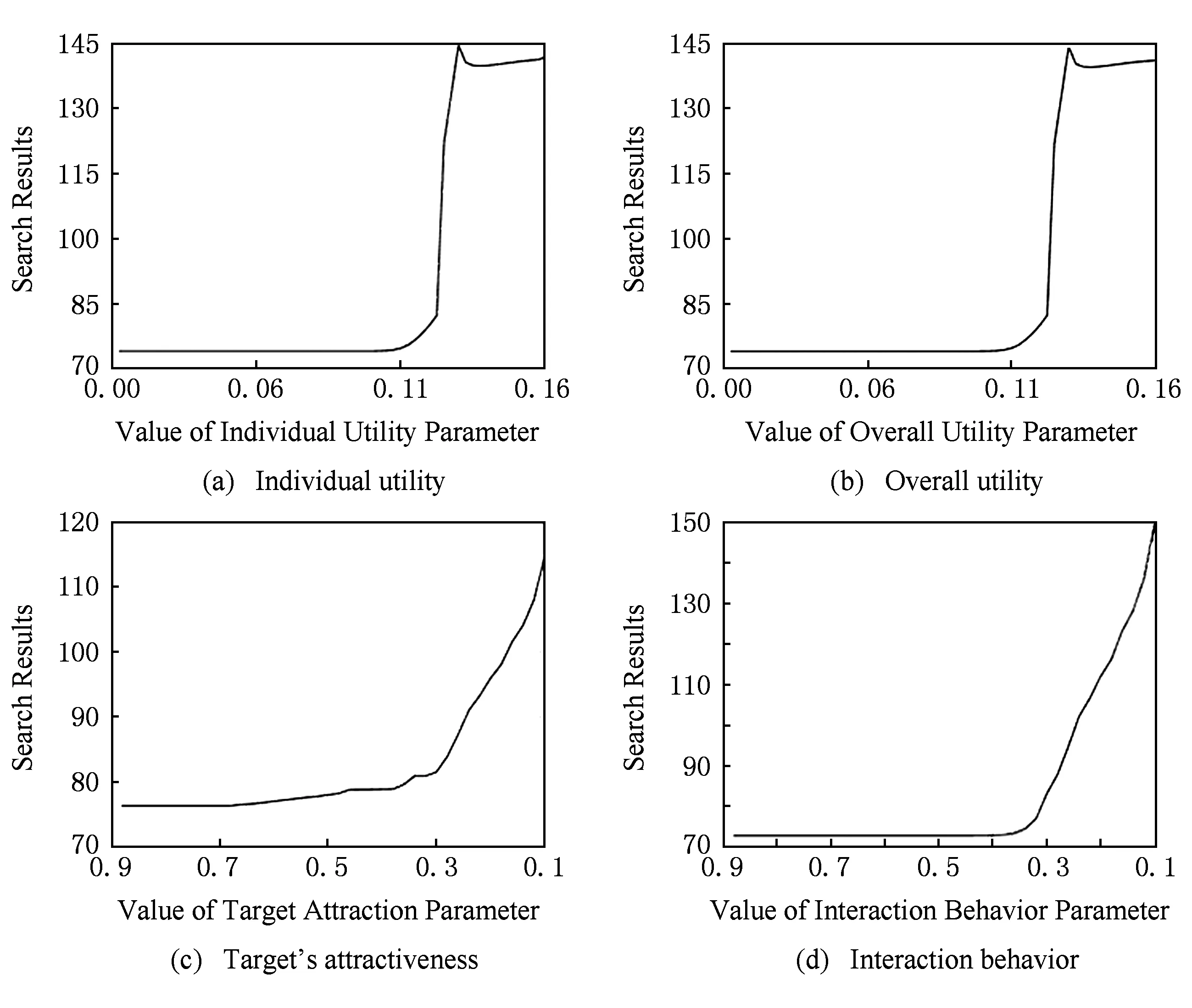
③ While(t ④ Ift=X/*X为修改年龄因子的阈值*/ ⑤ε=αε; /*α为修改年龄因子的参数*/ ⑥ 根据式(7)~(11)分别计算uij,J(t),P(t),Q(t),E(t); ⑦ 生成随机值,随机修改某一电导率dij的值; ⑨ If Δu>0 6.1算法收敛性分析 本文在PEO中引入了动力学机制,即伴随着演化过程的推进,由于系统存在能量开销,系统的总能量将逐渐减小至0.目标状态产生的吸引力将不断推动着系统的演化,同时吸引力函数也会随之变化.当吸引力逐渐变化至消失时,整个系统的能量演化过程将趋于稳定收敛状态.由于算法数学模型的构建基于微分方程,则该算法的收敛性稳定性可以使用Lyapunov稳定性理论来证明. Lyapunov稳定性理论,函数L(x)具有2个特点: 1)L(x)>0; 那么L(X(t))称为Lyapunov的备选方程,X满足Lyapunov渐进稳定性. 证明. 根据Lyapunov稳定性理论,定义一个Lyapunov方程L(D(t)): L(D(t))D(t), 那么D(t)的更新公式为 那么,根据dij∈[0,1],可以得知D(t)>0恒成立,所以L(D(t))>0也恒成立. 其中, 那么, 即: 证毕. 6.2年龄因子控制参数分析 定理2. 当ε比较小的情况下,目标吸引力函数P(t)将会使得距离目标成功度最小的管道向着最优结构的目标演化,即个体效用最小的管道增加. 证明. 设定S(t)为个体效用最小的管道,即: 那么,就存在不等式成立: 由此,对上述不等式的符号两边分别取对数,可以得到: n. 由于nn是常数,而且ε很小,那么我们可以通过移项得到: 由此可得,目标吸引力函数P(t)作用于个体效用最小的个体,所以当增加目标吸引力函数的值时,就可以使得个体效用值最小的个体向最优解目标移动.于是可以通过修改ε的值来调整目标吸引力函数的大小,以此来优化个体效用值最小的个体从而达到优化系统的整体效用的效果,即ε可控制算法的收敛速度. 证毕. 本实验使用TSP问题作为测试问题,采用TSPLIB数据集,将PEO算法的实验结果和其他算法进行对比,以此证明算法PEO的收敛性和有效性,并对算法的参数进行实验分析.实验环境为联想深腾6800高性能计算集群,该计算集群共拥有8个计算节点和1个总控节点.每个计算节点都是一台高性能服务器,内存24 GB,四核2.4 GHz中央处理器.每个节点服务器的操作系统都是Red Hat Enterprise Linux 7. 7.1实验证明算法的有效性 为了验证算法的有效性,本实验采用不同规模的TSPLIB实例进行实验,对于算法PEO,GA,PSO,ACO的参数设置见表2所示.其中,PEO的参数分别为个体效用权重λ1、整体效用权重λ2、目标对整体的吸引力权重λ3、个体间交互行为权重λ4、吸引力影响因子ε、吸引力更正参数α、年龄因子阈值参数r.GA的参数分别为种群的个数pnum、交叉概率pc、变异概率pm、选择概率ps[32].PSO的参数为种群规模pnum、惯性因子w(Mt是最大迭代次数,t代表当前迭代次数)、个体权重影响c1和全局权重影响c2[33].ACO的参数依次分别为信息素的重要程度α、启发式因子的重要程度β、信息素的挥发程度ρ、信息素增强系数Q和种群规模pnum[32].本实验通过比较在相同实例下,PEO与GA,SA,PSO和ACO的实验结果和性能来验证PEO的有效性. Table 2 Parameter for Each Algorithm表2 各算法参数表 算法PEO,GA,PSO和ACO在不同规模数据集下进行实验的运行时间和寻优结果如表3所示. Fig. 4 The experimental results on ulysses16图4 算法PEO,GA,PSO,ACO在数据集ulysses16上的实验 Table 3 Experimental Results Comparsion AmongPEO,GA,PSO,ACO 表3中的每列分别表示30次重复试验的TSPLIB实例、对比算法、平均寻优时间、平均寻优结果.由表3分析可得: 1) 算法PEO,GA,PSO和ACO在不同规模数据集上均能求解,但寻优能力不尽相同.其中,PEO的全局能力相对优于其他3种算法. 2) 当要处理的数据集规模不大的时候,各算法寻优能力相当,但PEO的寻优时间相对较短,收敛速度很快. 3) 对于复杂的大规模数据集来说,PEO,PSO和ACO算法的寻优能力相对较好,但PEO算法在并行计算求解过程中,耗费的时间代价较小,算法解决问题的时间优势明显,能够在很快时间内对TSP问题求解. 4种算法的寻优时间和寻优结果对比如图4、图5所示.由于TSP问题的最优解通常具有相邻城市相连且尽量路径间避免交叉的特点,通过图4、图5分析可得,PEO的寻优能力优于GA,PSO以及ACO算法,能够有效的避免算法陷入局部最优.此外,由于PEO算法在寻优过程中,根据系统的动力学特性会不断地进行优化调整,寻优能力不受制于算法的初始化过程中的设定,最终系统会趋于稳定而得到最优解,所以PEO算法具有鲁棒性的特点. Fig. 5 The experimental results on att48图5 算法PEO,GA,PSO,ACO在数据集att48上的实验 Fig. 6 Solution results of PEO algorithm on different scale data sets图6 算法在不同规模数据集上的实验结果 图6分别是算法PEO在数据集eil76,ch130,att532和pcb3038上的实验结果.根据图6分析可得,PEO算法在小规模或一般规模的数据集上都能取得较好的寻优结果,在较大规模和大规模的数据集上依然能够对问题求解,表现出了较好的寻优能力. 通过图7分析可得算法PEO针对不同规模的数据集,寻优时间都相对其他算法处于较低水平,收敛速度较快.根据图8可知,PEO相对于其他算法在不同规模的问题上都能得到相对较好的结果. Fig. 7 Algorithm’s optimal time comparison chart图7 算法的寻优时间对比图 Fig. 8 Algorithm’s optimal value comparison chart图8 算法的寻优结果对比图 7.2实验证明算法收敛性 为了证明算法的收敛性,算法PEO对于数据集ulysses16进行了实验,分析了其各管道电导率和压力差的变化趋势.由图9分析可得,各边电导率伴随迭代次数的增加在区间[0,1]内不断变化,各管道的压力差也在逐渐变化.在迭代次数100次到150次之间,电导率的值逐渐处于收敛状态,构成目标路径解的管道电导率逐渐收敛至1趋于稳定.相反,其他的管道的电导率将在演化迭代中逐渐收敛到0而不再发生变化. Fig. 9 The change tendency of each pipe’s conductivity and pressure difference in ulysses16图9 电导率和压力收敛变化图 7.3引入年龄因子和扰动机制的实验效果 通过对比PEO未引入年龄因子机制及扰动机制和引入年龄因子机制及扰动机制的实验结果,由图10分析可得:未引入年龄因子机制及扰动机制的算法会过早的陷入早熟收敛,导致收敛的速度很快;引入年龄因子机制及扰动机制求解的精度有所提升,但是收敛的速度变慢. 7.4算法参数分析 Fig. 10 The validity analysis of age factor and disturbance mechanism图10 年龄因子和随机扰动机制的有效性分析 本节主要对PEO的主要参数进行实验分析,采用了ulysses16数据集,将各参数的变化区间分别设定为:λ1∈[0.01,0.9],λ2∈[0.01,0.9],λ3∈[0.1,0.9],λ4∈[0.1,0.9]进行实验. 通过图11分析可得:参数λ1和λ2的取值范围在[0.1,0.2]时,算法的寻优效果相对较好;参数λ3和λ4的取值范围在[0.6,0.9]和[0.4,0.9]时,算法能够得到较好的寻优效果.其中,参数α的大小是用来控制年龄因子的阈值范围的,本实验α=0.8.由于算法的状态和年龄阶段会伴随要解决问题的规模大小的变化而发生变化,所以算法的年龄因子参数α需要根据实验的效果和问题求解的需求进行一定范围的调整. Fig. 11 PEO’s parameter analysis diagram图11 各参数的设定对寻优效果的影响 本文提出了基于能量机制的多头绒泡菌优化算法PEO,根据系统的动力学特点,其演化过程伴随着能量的耗损趋于稳定,为算法收敛提供了严密的理论依据.此外,提出年龄因子模型和引入扰动机制,以提高算法的寻优能力,避免算法早熟,防止寻优过程陷入局部收敛.通过实验证明PEO在针对不同规模复杂程度的问题能够快速收敛,具有很好的求解能力,可以有效避免智能算法常见的早熟收敛情况.对于设定年龄因子的阈值方面还需进一步改进,在一定的迭代次数下,当前最优解和目标解之间还是存在一定的提升空间,本文的工作还只处于初步阶段,将会进行进一步的研究. [1] Allen P G. New frontiers in bioscience[J]. Science, 2016, 352(6281): 11 [2] Kulkarni R V, Venayagamoorthy G K. Particle swarm optimization in wireless-sensor networks: A brief survey[J]. IEEE Trans on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2011, 41(2): 262-267 [3] Luo Chaomin, Yang S X. A bioinspired neural network for real-time concurrent map building and complete coverage robot navigation in unknown environments[J]. IEEE Trans on Neural Networks, 2008, 19(7): 1279-1298 [4] Arena P, Fortuna L, Frasca M, et al. An adaptive, self-organizing dynamical system for hierarchical control of bio-inspired locomotion[J]. IEEE Trans on Systems, Man, and Cybernetics, Part B (Cybernetics), 2004, 34(4): 1823-1837 [5] Bandyopadhyay S, Saha S, Maulik U, et al. A simulated annealing-based multiobjective optimization algorithm: AMOSA[J]. IEEE Trans on Evolutionary Computation, 2008, 12(3): 269-283 [6] Herrera-Viedma E, Chiclana F, Herrera F, et al. Group decision-making model with incomplete fuzzy preference relations based on additive consistency[J]. IEEE Trans on Systems, Man, and Cybernetics, Part B (Cybernetics), 2007, 37(1): 176-189 [7] Zhang Shiwen, Li Zhiyong, Chen Shaomiao, et al. Dynamic multi-objective optimization algorithm based on ecological strategy[J]. Journal of Computer Research and Development, 2014, 51(6): 1313-1330 (in Chinese)(张世文, 李智勇, 陈少淼, 等. 基于生态策略的动态多目标优化算法[J]. 计算机研究与发展, 2014, 51(6): 1313-1330) [8] Durbin R, Willshaw D. An analogue approach to the travelling salesman[J]. Nature, 1987, 326(16): 689-691 [9] Dorigo M, Gambardella L M. Ant colony system: A cooperative learning approach to the traveling salesman problem[J]. IEEE Trans on Evolutionary Computation, 1997, 1(1): 53-66 [10] Dorigo M, Birattari M, Stutzle T. Ant colony optimization[J]. IEEE Computational Intelligence Magazine, 2006, 1(4): 28-39 [11] Poli R, Kennedy J, Blackwell T. Particle swarm optimization[J]. Swarm Intelligence, 2007, 1(1): 33-57 [12] Booker L B, Goldberg D E, Holland J H. Classifier systems and genetic algorithms[J]. Artificial Intelligence, 1989, 40(1/2/3): 235-282 [13] Kirkpatrick S, Gelatt C D, Vecchi M P. Optimization by simmulated annealing[J]. Science, 1983, 220(4598): 671-680 [14] Yang Gang, Yi Junyan, Yang Nan. Elastic net with stochastic noise strategy and time-dependent parameters for TSP[C] //Proc the 7th Int Conf on Natural Computation. Piscataway, NJ: IEEE, 2011: 426-430 [15] Yan Jianfeng, Li Na, Li Weihua, et al. Hybrid ant colony algorithm based on scale compression[C] //Proc of 2007 Int Conf on Machine Learning and Cybernetics. Piscataway, NJ: IEEE, 2007: 885-889 [16] Su Jinrong. Improved particle swarm optimization for multi-object traveling salesman problems[C] //Proc of the 7th Int Conf on Natural Computation. Piscataway, NJ: IEEE, 2011: 1175-1179 [17] Lu Jingui, Fang Ning, Shao Dinghong, et al. An improved immune-genetic algorithm for the traveling salesman problem[C] //Proc of the 3rd Int Conf on Natural Computation (ICNC 2007). Piscataway, NJ: IEEE, 2007: 297-301 [18] Ye Gao, Rui Xue. An improved simulated annealing and genetic algorithm for TSP[C] //Proc of the 5th IEEE Int Conf on Broadband Network & Multimedia Technology. Piscataway, NJ: IEEE, 2013: 6-9 [19] Arshad S, Yang Shengxiang. A hybrid genetic algorithm and inver over approach for the travelling salesman problem[C] //Proc of IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2010: 1-8 [20] Saadatmand-Tarzjan M, Khademi M, Akbarzadeh-T M R, et al. A novel constructive-optimizer neural network for the traveling salesman problem[J]. IEEE Trans on Systems, Man, and Cybernetics, Part B (Cybernetics), 2007, 37(4): 754-770 [21] Hu Xiaomin, Zhang Jun, Chung H S H, et al. SamACO: variable sampling ant colony optimization algorithm for continuous optimization[J]. IEEE Trans on Systems, Man, and Cybernetics, Part B (Cybernetics), 2010, 40(6): 1555-1566 [22] Nakagaki T, Yamada H, Tóth á. Maze-solving by an amoeboid organism[J]. Nature, 2000, 407(6803): 470-470 [23] Nakagaki T, Yamada H, Toth A. Path finding by tube morphogenesis in an amoeboid organism[J]. Biophysical chemistry, 2001, 92(1): 47-52 [24] Nakagaki T, Iima M, Ueda T, et al. Minimum-risk path finding by an adaptive amoebal network[J]. Physical review letters, 2007, 99(6): 068104 [25] Tero A, Takagi S, Saigusa T, et al. Rules for biologically inspired adaptive network design[J]. Science, 2010, 327(5964): 439-442 [26] Song Yuning, Liu Liang, Ma Huadong, et al. Physarum optimization: a new heuristic algorithm to minimal exposure problem[C] //Proc of 2012 IEEE Wireless Communications and Networking Conf (WCNC). New York: ACM, 2012: 419-422 [27] Tero A, Kobayashi R, Nakagaki T. A mathematical model for adaptive transport network in path finding by true slime mold[J]. Journal of Theoretical Biology, 2007, 244(4): 553-564 [28] Bonifaci V, Mehlhorn K, Varma G. Physarum can compute shortest paths[J]. Journal of Theoretical Biology, 2012, 309: 121-133 [29] Tero A, Yumiki K, Kobayashi R, et al. Flow-network adaptation in Physarum amoebae[J]. Theory in Biosciences, 2008, 127(2): 89-94 [30] Mersch D P, Crespi A, Keller L. Tracking individuals shows spatial fidelity is a key regulator of ant social organization[J]. Science, 2013, 340(6136): 1090-1093 [31] Feng Xiang, Lau F C M. A parallel evolutionary approach to multi-objective optimization[C] //Proc of 2007 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2007: 1199-1206 [32] Shuang Bing, Chen Jiapin, Li Zhenbo. Study on hybrid PS-ACO algorithm[J]. Applied Intelligence, 2011, 34(1): 64-73 [33] Zhang Jiangwei, Xiong Wei. An improved particle swarm optimization algorithm and its application for solving traveling salesman problem[C] //Proc of 2009 WRI World Congress on Computer Science and Information Engineering. Piscataway, NJ: IEEE, 2009: 612-616 PhysarumDynamicOptimizationAlgorithmBasedonEnergyMechanism Liu Yang1, Feng Xiang1,2, Yu Huiqun1, and Luo Fei1 1(SchoolofInformationScienceandEngineering,EastChinaUniversityofScienceandTechnology,Shanghai200237)2(SmartCityCollaborativeInnovationCenter,ShanghaiJiaoTongUniversity,Shanghai200240) With the rapid development of artificial intelligence and big data, the explosive growth of big data and problem has grown in complexity, which leads to parallel intelligent computing demand increasing. Traditional theoretical models and methods are faced with severe challenges. Physics law and biological method inspired from nature has gradually become a hot spot in the present new period. Inspired by the foraging behavior of physarum, an dynamic algorithm based on energy mechanism is presented. Physarum-energy dynamic optimization algorithm (PEO) is being raised for overcome the drawbacks of physarum algorithm. According to physarum’s dynamic characteristics, the energy mechanism is introduced in PEO which aims to overcome the shortcomings of the existing physarum algorithm, such as its poor information interaction ability in whole. In addition, PEO develops age factor concept and disturbance mechanism, in order to adjust PEOs optimization ability and convergence speed in different age stages, and the convergence of algorithm model is proved through theoretical point of view. Finally, the validity and convergence of PEO are proved by experiments in TSP data set, and the main parameters of PEO are analyzed through experiments. When faced with complex problems, the simulation result comparison analysis between PEO and other optimization algorithms show that PEO is significantly better than other algorithm and PEO has the capability of high accuracy and fast convergence. physarum-energy dynamic optimization algorithm (PEO); energy mechanism; age factor; traveling salesman problem Liu Yang, born in 1993. Master candidate in the School of Information Science and Engineering, East China University of Science and Technology. Student member of CCF. Her main research interests include parallel and distributed computing, artificial intelligence and pattern recognition. Feng Xiang, born in 1977. PhD, professor and PhD supervisor in the School of Information Science and Engineering, East China University of Science and Technology. Member of CCF. Her main research interests include mechanics-related nature inspired algorithm, parallel and distributed computing and computer networks. Yu Huiqun, born in 1967. PhD, professor and PhD supervisor in the School of Information Science and Engineering, East China University of Science and Technology. Member of CCF. His main research interests include software engineering, trustworthy computing and formal methods (yhq@ecust.edu.cn). Luo Fei, born in 1978. PhD, associate professor in the School of Information Science and Engineering, East China University of Science and Technology. Member of CCF. His main research interests include distributed computing and embedded systems (luof@ecust.edu.cn). 2017-05-23; :2017-07-03 国家自然科学基金项目(61472139,61462073);上海市经济和信息委员会信息化发展专项资金项目(201602008);上海市智慧城市协同创新中心开放基金项目 This work was supported by the National Natural Science Foundation of China (61472139,61462073), the Information Development Special Funds of Shanghai Economic and Information Commission (201602008), and the Open Funds of Shanghai Smart City Collaborative Innovation Center. 冯翔(xfeng@ecust.edu.cn) TP18
6 算法理论分析
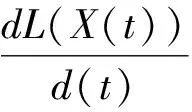
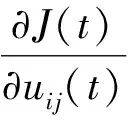
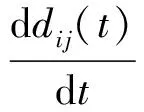
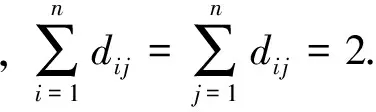
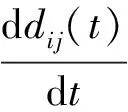
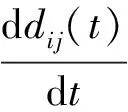
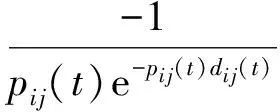
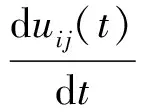
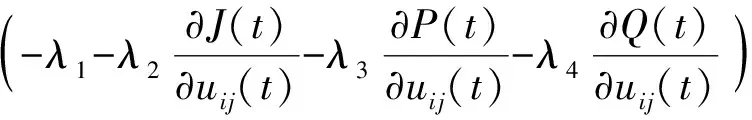
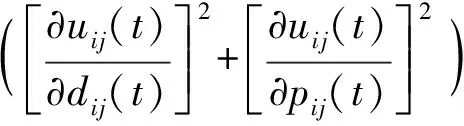
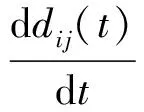
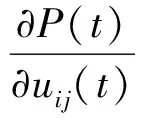
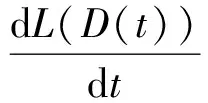
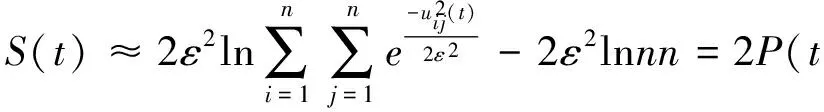
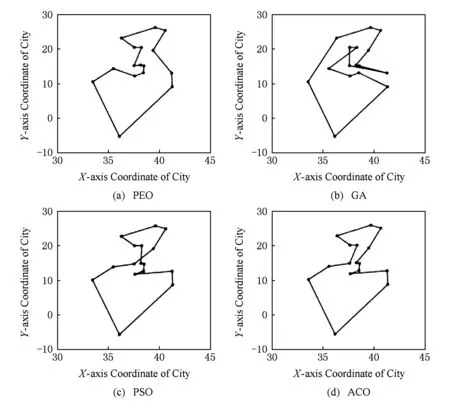
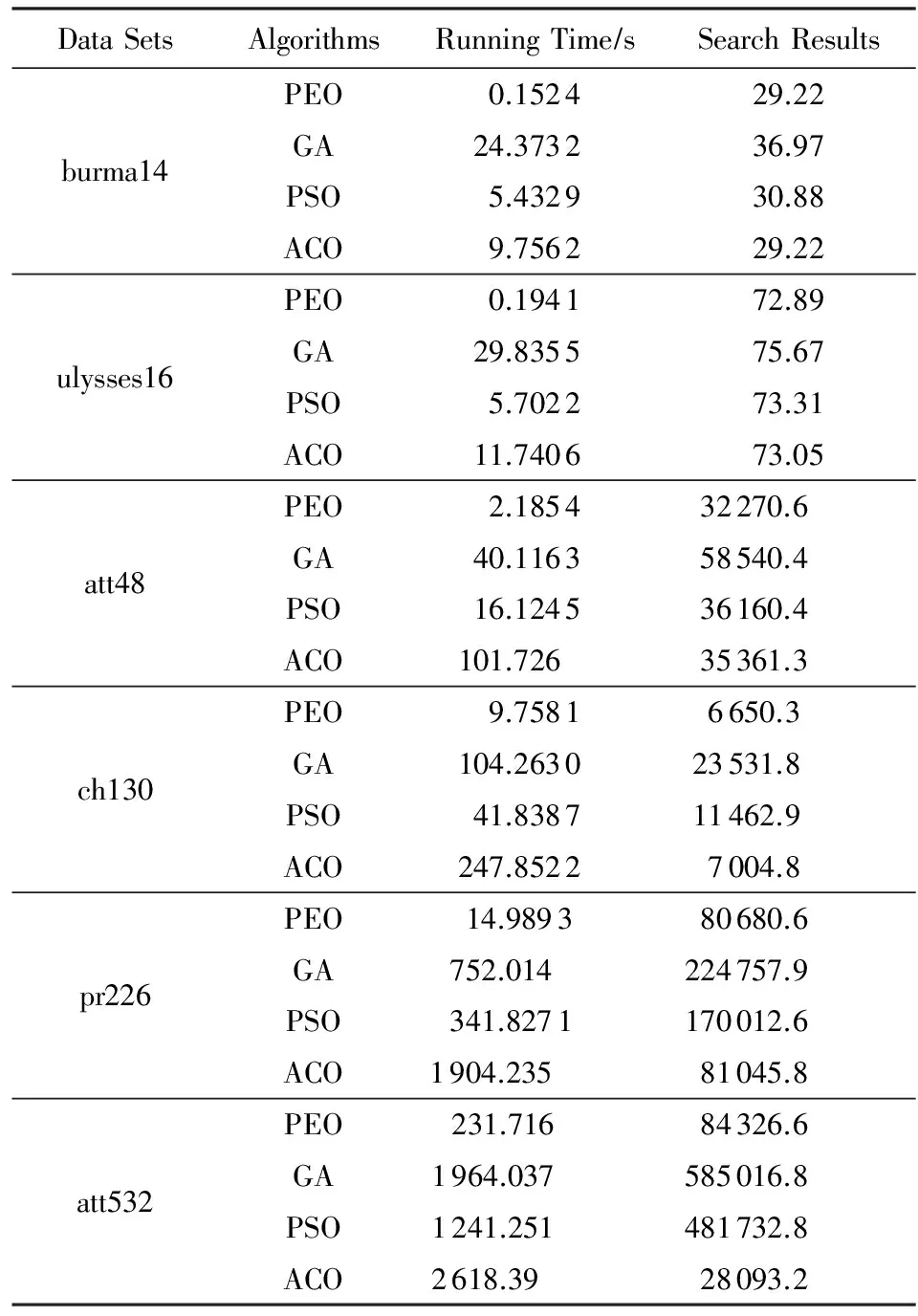
7 实验分析

8 总结与展望




