基于表示学习和语义要素感知的关系推理算法
2017-08-31韩明皓杨晓慧吴祖峰
刘 峤 韩明皓 杨晓慧 刘 瑶 吴祖峰
(电子科技大学信息与软件工程学院 成都 610054) (qliu@uestc.edu.cn)
基于表示学习和语义要素感知的关系推理算法
刘 峤 韩明皓 杨晓慧 刘 瑶 吴祖峰
(电子科技大学信息与软件工程学院 成都 610054) (qliu@uestc.edu.cn)
基于知识表示的关系推理方法研究是近年来统计关系学习和知识图谱领域共同关注的热点.通过对当前流行的基于知识表示的推理模型进行比较,分析了现有模型所普遍采用的基本假设存在的不合理之处,即忽视了实体与关系在语义上的多样性.据此提出了一种新的关系推理建模假设:实体对之间的每种关系反映的是两侧实体在某些特定方面的语义关联,通过对实体向量的语义方面要素进行选择性加权,可以实现对不同关系语义的表示和区分.根据该假设提出了一种新的关系推理建模方法,采用非线性变换的方法来解决表示学习中的语义分辨率问题.在公开数据集上的实验结果表明:所提出的算法对复杂关系类型和相关实体具有良好的语义区分能力,能有效提高知识图谱上的关系推理准确率,性能显著优于目前主流的相关工作.
统计关系学习;关系推理;表示学习;知识图谱;多元关系数据挖掘
本文研究的是知识图谱上的关系推理问题.关系推理任务的目标是基于知识图谱中已有的知识,采用统计机器学习方法自动推理实体对之间可能存在的关系.它既是统计关系学习领域长期关注的基础理论问题,也是知识图谱领域的研究热点[1].
知识图谱是一个由实体与关系构成的结构化语义知识库,其中的知识元素以(实体,关系,实体)三元组的形式表达和存储,实体间通过关系相互联结,构成网状知识结构[2].知识图谱技术在自然语言处理、智能信息检索和知识工程等领域具有核心基础地位,近年来受到学术界的广泛关注[3].然而,制约知识图谱应用水平的一个关键问题是知识的不完备性,虽然近年来谷歌Knowledge Vault、微软Satori和IBM Watson等知识图谱项目不断刷新知识规模记录,现有的知识图谱仍然存着大量的信息缺失[4].
关系推理技术可以直接应用于知识图谱的自动化补全,也可以与开放域信息抽取(open information extraction, OIE)技术相结合,用于对信息抽取结果进行质量评估,提高知识图谱构建的自动化水平[1].
当前关系推理方法的研究思路主要有2类:基于逻辑规则的关系推理模型和基于表示学习的关系推理模型[5].随着关系推理算法研究不断取得新进展,部分成果已经在主流商业产品中取得应用,例如Knowledge Vault项目就采用了逻辑规则模型与表示学习模型相结合的混合模型来进行知识质量评估[6].
与基于逻辑规则的关系推理模型相比,基于表示学习的关系推理模型能够更有效地利用知识图谱中已有的知识进行推理建模[7].而且,随着深度学习技术在知识表示学习领域的应用不断深入,基于表示学习的关系推理算法研究也取得了快速发展,是近年来关系推理研究领域重点聚焦的热点问题[5].
然而,通过文献调研我们发现,现有的基于表示学习的关系推理模型在对实体关系三元组(h,r,t)进行关系推理时均采用了Bordes等人提出的向量表达基本假设:h+r=t,因此存在一个共性缺陷,即模型无法表达关系语义的多样性,建模方式的僵化导致算法对位于关系同一侧的多个实体的分辨率较差.
这种理论缺陷典型的表现是当此类算法在处理“一对多”和“多对一”类型关系(对关系类型的定义详见2.1)时,如果对于关系两侧实体分别实施替换干扰,得到的推理性能表现不均衡,对于“多”侧实体的区分能力明显较差.本文实验部分将对此进行详细讨论.另一个典型表现是当实体间存在多种关系时,会出现语义上的悖论.例如,若实体对(h,t)之间既有“父子”关系,又有“校友”关系,由于实体的向量表达是确定的,则根据基本假设h+r=t可以得出“父子=校友”的错误结论.
针对上述问题,本文提出一种新的建模思路如下:将通过表示学习得到的实体向量中的元素视为其语义方面要素(aspect factors),在不同关系代表的语义环境下,关系向量中的每个元素可由关系两侧实体向量中的对应元素线性组合得到.籍此可以修正基于表示学习的关系推理算法的基本假设,提高模型对关系语义多样性的区分能力.论文的主要贡献包括:
1) 提出了一种新的关系推理建模假设:实体对(h,t)之间的每种关系反映的是关系两侧实体在某些特定的语义方面要素上的关联,可以通过对实体的语义方面要素进行选择性加权来表达和区分.
2) 设计了2种新的关系推理算法,对上述假设进行了实验验证,实验结果表明所提算法的综合性能表现显著优于当前主流的相关工作.
1 相关工作
早期的关系推理方法研究主要基于一阶谓词逻辑规则和贝叶斯算法,通过将人工编写的一阶谓词逻辑规则与不同类型的概率图模型相结合,依据所生成的逻辑网络进行推理获得新的知识[8].代表性工作包括Markov逻辑网络模型[9]和基于贝叶斯网络的概率关系模型[10].这类模型能够在小规模领域知识库上取得较高的关系推理准确性,缺点在于依赖专家构建逻辑规则,且模型在推理过程中的计算复杂度较高,难以适应大规模知识库上关系推理任务要求[11].
1.1基于逻辑规则的关系推理模型
为解决大规模知识图谱中关系推理的效率问题,Lao等人在基于一阶Horn子句推理的FOIL(first order inductive learner)算法基础上提出了一种路径排序算法(path ranking algorithm, PRA)[12].PRA算法采用抽象的实体间关系路径取代了具象的Horn子句作为关系推理的依据,并采用随机采样的方式替代穷举搜索以提高计算效率.PRA算法不仅保持了FOIL算法的关系推理准确性,而且提高了模型的计算效率.
随后,Gardner等人指出PRA算法在计算关系路径概率时的计算开销过大,并据此采用特征空间二值化、增加自定义特征模式以及采取广度优先搜索等方式对PRA算法进行了改进,提出了准确性和计算效率更好的SFE(subgraph feature extraction)算法[13].
然而,SFE算法在推理准确性上仍无法与当前主流的基于表示学习的关系推理算法抗衡.Liu等人指出了PRA和SFE算法所采用的关系单向性假设存在的问题,并采用双层随机游走策略提高了算法对关系路径的采样覆盖率,所提出的层次化随机游走推理模型(hierarchical random walk inference, HiRi)在公开数据集上取得了优于表示学习模型的性能表现[7].
总体说来,逻辑推理模型的发展趋势是逐渐摒弃对人工规则的依赖,转而借助模式识别方法进行规则特征发现,并采用机器学习方法进行特征建模.制约逻辑推理算法研究的主要问题是图算法的计算复杂度较高,导致方法可扩展性差.而且知识图谱中的节点度的分布服从长尾分布,即只有少量的实体与关系拥有较高的出现频率,而大部分实体关系的出现频率较低.由此导致的数据稀疏性问题对逻辑推理算法的性能影响较大[5].因此目前学术界主要关注对数据稀疏性不敏感,且算法可并行的表达推理算法.
1.2基于表示学习的关系推理模型
随着word2vec和GloVe等“词向量表达”模型相继在一系列自然语言处理任务中取得进展[14-15],表示学习方法近年来受到了广泛关注.在关系推理领域,以TransE算法为代表的关系推理模型,因其具有推理准确性高和算法可并行等优点而成为近期研究热点,目前仍在快速发展过程中[16].
TransE模型参考了Nickel等人提出的RESCAL张量分解模型(tensor factorization model)[17].该模型采用三阶张量对知识图谱中的事实(h,r,t)进行建模,参数模型的函数表达为
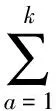
(1)
其中,h,t∈k为三元组的头、尾实体在k维空间的向量表达,Wr∈k×k表示关系r的权重矩阵.
受RESCAL模型启发,Bordes等人提出了基于结构化表达的SE(structured embedding)关系推理算法[18].参数模型的函数表达如下:
(2)
其中,Mrh和Mrt分别表示关系r关于头和尾实体的线性变换.由于SE和RESCAL算法在大规模真实数据集上的推理准确性较低,Bordes等人受word2vec词表达算法的启发提出了TransE建模假设,放弃了RESCAL算法采用关系矩阵变换的实体映射方式,转而采用h+r=t的方式进行推理[16].参数模型为
(3)
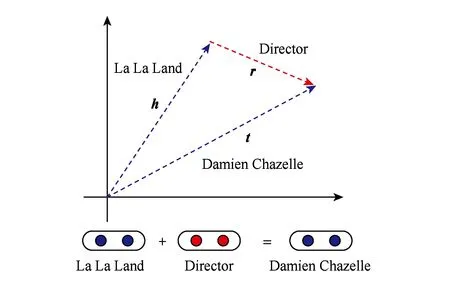
Fig. 1 The example of TransE model图1 TransE模型示例
TransE算法因其计算效率高(可并行)和算法召回率高而受到学术界的高度关注[1].然而该算法在处理复杂关系类型时存在性能瓶颈,为改进TransE算法性能,学术界近年来付出了大量的努力[5].
例如Wang等人提出的TransH算法允许实体在不同的关系下采用不同的向量表达[19].基本思路是在TransE基本假设基础上增加实体映射,即首先将实体映射到对应关系r的超平面中:
(4)
其中,wr∈k表示由关系r所确定的超平面的单位法向量.然后根据hr+r=tr基本假设进行建模.
Fan等人提出的TransM模型[20],通过向优化目标函数中引入与关系类型相关的权重因子,以强化TransE模型对实体的区分能力.参数模型如下:
(5)
受上述工作启发,Lin等人综合借鉴TransH,TransM和RESCAL算法的思路,提出了TransR算法和改进的CTransR算法[21].基本思路是将实体与关系视为不同类型的对象,应分别将其投影到不同的向量空间中,TransR所使用的实体映射为
hr=Mrh;tr=Mrt,
(6)
其中,Mr∈d×k表示关系r的线性变换参数矩阵,其作用是将实体的向量表达从k维空间变换到关系r所在的d维空间.由于TransR算法的参数复杂度较高,为了降低模型复杂度,提高算法对大规模知识图谱推理任务的适用性,Lin等人还进一步提出了改进的CTransR算法,通过将知识图谱中的实体按从属的关系类型进行聚类,在提高计算效率的同时也增加了实体在不同关系上下文的区分度,在FB15K等数据集上的实验性能优于主流相关算法[21].
1.3对相关工作的讨论
除了基于逻辑规则和基于表示学习的关系推理方法外,学术界还提出了一些新的解决方案.例如,Socher等人针对SE模型对知识库结构信息利用不足的缺点提出了单层感知机模型(single layer model, SLM),SLM模型能够对实体在特定关系语义下的相关性进行建模,参数模型表达为:
f(h,r,t)=rTg(Mrhh+Mrtt),
(7)
其中,Mrh和Mrt分别表示关系r关于头实体和尾实体的映射矩阵.激活函数g(·)为双曲正切(tanh)函数.针对SLM模型表示学习能力不足的缺点,Socher等人进一步提出了神经张量模型(neural tensor networks, NTN),通过将SLM中的线性变换层替换为双线性张量,进一步提高了关系推理准确性[22].然而,NTN算法的张量计算复杂度非常高,且由于模型参数复杂度过高,易导致参数训练欠拟合,所以需要大量的训练数据,进一步导致模型训练困难.
此外,Lin等人尝试将逻辑推理与表达推理方法相结合,提出了PtransE算法[23].思路是将知识图谱中的关系路径与关系的向量表达联系起来,将逻辑推理规则视为向量加法操作.评分函数为
f(h,r,t)=E(h,r,t)+E(h,P(h,t),t),
(8)
其中,P(h,t)={p1,p2,…,pN}表示实体间关系路径集合,pi=(r1,r2,…,rk)为实体间的一条路径,E(h,r,t)等价于式(3),E(h,P(h,t),t)计算为
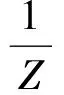
(9)
综上,基于表示学习的关系推理算法研究是近年来关系推理领域关注的热点问题.基本思路是将实体与关系对象包含的语义信息表示为低维空间中的实值向量,进而用于关系推理计算.TransE算法是表达推理模型的典型代表,因其计算效率高且推理准确性高而备受关注,学术界对其进行了反复研究改进[5].
然而,通过对比以上算法改进工作可看到,改进后的算法均未能从根本上解决TransE基本假设中存在的矛盾,即忽视实体与关系在语义上的多样性.例如,TransH和TransR算法,虽然采用了不同的线性变换机制修正实体向量,但最终仍是基于h+r=t基本假设进行模型参数学习.由于该假设无法对实体在不同关系上下文环境下的语义做出区分,因此在得到实体的向量表达后,再试图通过线性变换来提高对实体间语义差别的分辨能力是非常困难的.
本文受上述相关工作的启发,提出用非线性变换的方法来解决表示学习的语义分辨率问题.通过将关系表达视为相关实体语义方面要素的加权组合,使算法模型既能够保留TransE基本假设的合理性,又同时具备对实体和关系在不同语义条件下的区分能力.在对算法性能进行测评时,考虑到PtransE和CTransR算法是目前公开报道的关系推理算法中性能表现最好的算法,但PtransE的关系路径采样过程计算复杂度过高,难以适应大规模知识图谱的推理任务要求,因此本文主要采用CtransR算法作为性能指标比较对象.此外,TransE算法被用作实验的Baseline,原因是该算法可以视为本文提出的算法的特例,通过比较二者的实验结果,可以加深对本文算法的理解.由于RESCAL算法目前被应用于一些商业知识库中,因此也将其作为实验比较对象,目的是通过对比二者的计算效率和推理准确率,揭示本文提出的算法模型的性能优势和实用价值.
2 基于表示学习的关系推理算法
符号系统说明:以符号KB表示知识图谱中已有的三元组集合.E和R分别表示知识图谱中的实体集合与关系集合.符号(h,r,t)∈KB表示一个已知事实.其中,符号h,t和r分别表示实体和关系的k维向量表达(embeddings),h称为头实体(head),t称为尾实体(tail),r表示实体对(h,t)之间的关系.
2.1算法设计思想
现有基于表示学习的关系推理算法大多基于Bordes等人提出的h+r=t基本假设,采用确定的实向量表达知识库中已有的实体与关系.本文认为这种确定的表示学习方式忽略了目标对象的语义多样性,是导致此类算法性能存在瓶颈的问题根源.
表1给出了TransE算法在4种关系类型上的实验结果,表中的Prediction with Head replacement字段表示对于给定三元组,通过替换头实体构造干扰列表的推理实验结果,Prediction with Tail replacement字段表示通过替换尾实体构造干扰列表得到的结果.
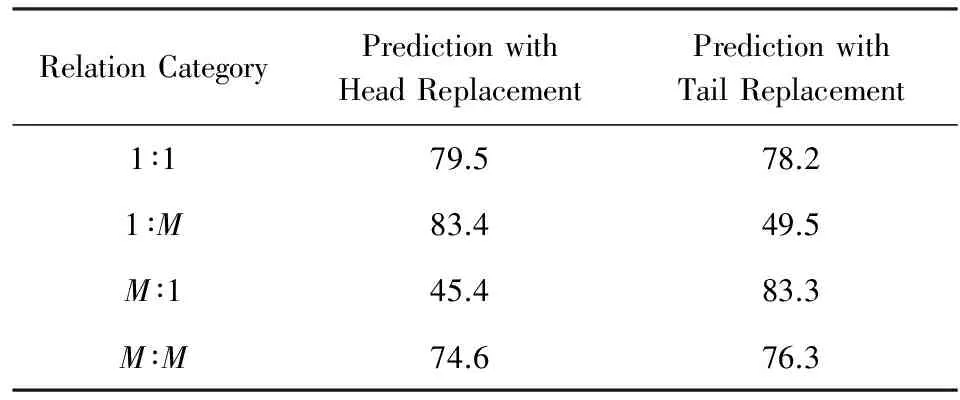
Table 1 hits@10 of TransE on FB15k Dataset
从表1可以看出,如果对关系两侧实体分别实施替换干扰,TransE算法在1∶M和M∶1等关系类型上的推理性能表现非常不均衡.表1中4种关系类型的划分依据为:对于给定关系ri定义一组参数为
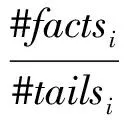
(10)
其中,factsi表示知识图谱中包含关系ri的三元组(事实)集合,#factsi表示factsi中的元素个数,#headsi和#tailsi分别表示factsi中包含的不同头、尾实体的个数.据此定义4种关系类型为
(11)
阈值η=1.5,以便与相关工作保持一致[7].从表1可以看出,TransE算法在处理一对多(1∶M)类型的关系(即一个头实体对应于多个尾实体)时,在尾实体一侧的性能表现显著低于头实体一侧.类似的情况也发生在多对一(M∶1)类型的关系推理任务中.这一现象表明,如果采用固定的向量表达来表示实体,在h+r=t假设下无法对相似实体的细微语义差别进行区分,导致推理结果存在语义分辨率问题.
为了进一步从理论角度阐述该假设存在的矛盾,假设实体对(h,t)之间存在多种不同的关系,以符号r1,r2,…,rn分别表示这些关系.则由TransE的基本假设h+r=t可以得出结论:
(12)
即关系r1,r2,…,rn的向量表示趋同,无法做语义上的区分.例如给定3个基本事实:(星球大战,导演,乔治·卢卡斯),(星球大战,制作人,乔治·卢卡斯)以及(星球大战,编剧,乔治·卢卡斯),由式(12)可知,TransE模型将对“导演”、“制作人”和“编剧”这3种关系得出相同的向量表达.其他基于TransE的表达推理模型也有类似的问题.
为解决该矛盾,需要修正算法的基本假设,提高模型对关系语义多样性的区分能力.
考虑到关系的普适性,即多个实体对之间可以共享同一种关系(如IsA关系和Affiliation关系等).本文将关系的向量表达视为不变量,将实体向量中的元素视为实体属性的方面要素(aspect factors).据此在h+r=t基本假设的基础上,提出新的假设如下:实体对(h,t)间的每种关系反映了两侧实体在某些特定的方面要素上的关联,可以通过对实体向量的方面要素进行选择性加权,以实现关系语义的区分.
该假设的合理性举例说明如下:以2个三元组为例:(特朗普,国籍,美国)和(特朗普,居住于,美国).若将实体向量视为不变量,则由h+r=t假设可以得出“国籍”=“居住于”的错误结论.
而根据本文提出的假设,即每种关系反映的是实体间某些特定方面要素的关联和差异,则可以有效解决上述问题.例如,“国籍”关系反映的是两侧实体间在法律、出生地等方面的从属关系,而“居住于”关系反映的是两侧实体间在工作、生活等方面的地理位置联系.本文认为,在实体的向量表达中,每个维度包含了不同的语义方面信息,通过对其进行适当的加权处理,可以实现对关系的表达和对关系语义的区分.据此提出关系推理算法的设计方案如下.
2.2算法描述
对于知识图谱中的每种关系ri∈k,定义与之相关的实体方面要素(语义)权重向量βi∈k,即关系ri代表的语义环境下,与实体向量的元素相对应的语义权重值所组成的向量.算法模型为
(13)
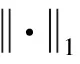
式(13)表示在给定的关系语境下,对三元组中的头尾实体向量采用相同的加权系数进行处理,以突出对应方面要素的影响,同时弱化不相关方面要素的影响.考虑到关系的有向性,关系两侧的实体也可能存在显著的语义差异,因此其向量表达的组成要素可能存在显著差异.以(特朗普,国籍,美国)为例,“国籍”关系的头实体是人物名实体,尾实体是国家名实体.人物的特征要素与国家的特征要素显然是无法实现一一对应的,因此本文进一步考虑对关系两侧的实体进行分别加权处理.即,对于知识图谱中的每种关系ri∈k,定义2个与之相关的实体方面要素权重向量k,分别用于对关系两侧实体集合的向量表达进行加权处理,算法模型为
(14)
从式(13)和(14)可以看出,当权重向量βi,βhi和βti的元素取值为1时,式(13)(14)2个算法等价于TransE模型.为便于区分上述模型,本文将式(13)称为统一加权模型(unified weighted model, UWM),将式(14)称为独立加权模型(independent weighted model, IWM).下面介绍模型的参数估计方法.
2.3模型训练方法
首先介绍训练样本的构造方法.本文遵循封闭世界假设[1],将知识图谱中已有的三元组视为正样本,正样本集合采用符号Δ表示.对于任意给定正样本(h,r,t)∈Δ,构造其负样本集合:
Δ′={(h′,r,t)|h′∈E∧(h′,r,t)∉Δ}∪
{(h,r,t′)|t′∈E∧(h,r,t′)∉Δ},
(15)
其中,(h′,r,t)和(h,r,t′)分别表示对样本(h,r,t)中的头、尾实体进行替换得到的三元组.得到训练样本集合后,采用边界最大所化(maximum margin)方法对本文提出的UWM算法与IWM算法的参数进行学习[19].设(h,r,t)∈Δ表示已知事实,(h′,r,t′)∈Δ′表示针对该给定事实构造的负样本.定义正负样本语义偏差函数为
J(h,r,t)=f(h,r,t)+γ-f(h′,r,t′),
(16)
其中,符号γ表示边界参数,用于设置正、负样本的语义误差间隔.据此进一步定义模型参数估计的优化目标函数为
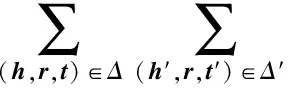
(17)
其中,函数max(x,y)返回x和y中较大的值.本文采用随机梯度下降(stochastic gradient descent, SGD)方法求解优化目标函数(17)的最优值,由此即可同步求得式(13)或式(14)的参数.
2.4算法复杂度分析
表2给出了本文提出的UWM和IWM算法模型以及一些经典相关算法的复杂度分析结果.其中,参数复杂度(parameter complexity)给出了模型中需要估计的参数个数,时间复杂度(time complexity)给出了采用SGD算法求解模型参数时,每轮迭代需要执行的浮点数加法和乘法的基本运算次数.

Table 2 Analysis of the Model Complexity表2 模型复杂度分析
表2中的符号Ne和Nr分别表示知识图谱中已有的实体数目与关系数目,N表示知识图谱中已有的三元组总数,k表示实体向量空间的维度,d表示关系向量空间的维度.包括TransE在内的多数表达推理算法将实体和关系投影到相同维度的空间中(即k=d),但也有部分算法采用不同维度的实体和关系向量表达(如TransR和CtransR算法).
从表2可以看出RESCAL模型和TransR模型的参数复杂度和计算时间复杂度均高出本文所提出的UWM算法和IWM算法约2个数量级(通常k和d的取值为102级别).同时可看出,UWM算法和IWM算法的参数复杂度与TransE相当(因为通常情况下Ne≫Nr),计算时间复杂度则比TransE算法高出约2个数量级.由此可见,本文提出2种关系推理算法的参数复杂度接近TransE算法,因此能够保持TransE算法对训练数据需求量较小,不易出现欠拟合问题的优点;计算时间复杂度则介于TransE和另外2种模型之间,但由于UWM算法和IWM算法不涉及张量运算和矩阵计算,因此易于实现并行,经GPU加速后,算法实际性能与TransE相当.因此,本文提出的关系推理算法简单高效,实用性好.
3 实验结果与分析
为验证本文提出的基本假设的有效性,即知识图谱中的关系可以通过对其相关联的实体向量的方面要素进行选择性加权来表达,本文选择了4种近期在关系推理领域引起广泛重视的相关工作进行实验比较,包括基于张量分解的代表性模型RESCAL算法,基于表示学习的代表性模型TransE算法,以及在TransE基础上改进得到的TransR算法和CTransR算法.并使用相关工作普遍采用的2组公开数据集对所提出的UWM算法和IWM算法进行测试.
① https://everest.hds.utc.fr/doku.php?id=en:transe
3.1实验数据
本文所使用的实验数据由法国贡比涅技术大学的Antoine Bordes等人整理并发布,分别称为WN18和FB15k数据集①.数据统计信息如表3所示.
其中,WN18数据集从WordNet知识库采样得到,WordNet是一个基于认知语言学,且覆盖范围较广的大型英文词汇数据库.WN18数据集包含18种关系类型、40 943个实体、151 442个三元组.上述三元组被随机划分为3组,分别用于模型参数训练(Train)、模型验证(Validation)和性能测试(Test).
FB15k数据集从Freebase采样得到,Freebase早期的知识来源是维基百科,后来被谷歌收购并维护,是当前规模最大的开源通用型知识库之一,知识范围覆盖现实世界中的各个方面.FB15k数据集包含1 345种关系、14 951个实体、592 213个三元组.同样地,FB15k中的三元组被随机划分为3组.
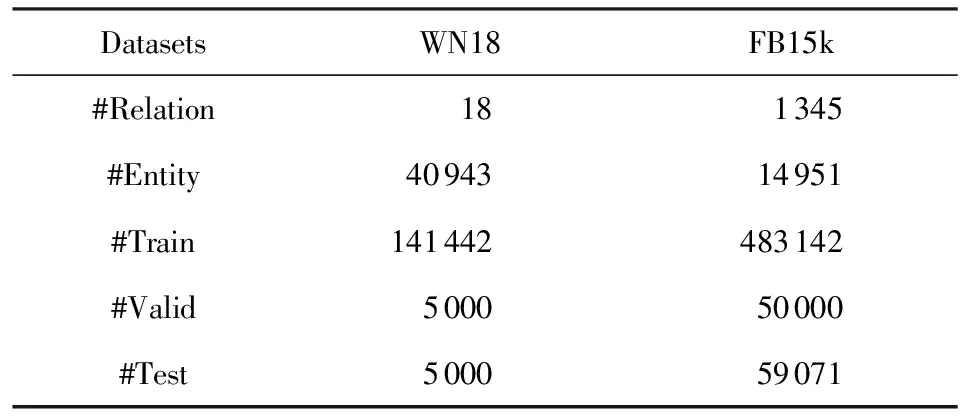
Table 3 Statistics of the Benchmark Datasets表3 基准数据集的统计信息
由于WN18包含的关系种类较少,且FB15k的知识来源更为丰富,因此本文将重点使用FB15k数据集对算法性能进行比较分析.经统计,取η=1.5,FB15k中1∶1类型的三元组数量约占1.51%,1∶M类型的三元组约占15.26%,M∶1类型的三元组数量约占9.49%,M∶M类型的三元组约占73.74%.
3.2实验方法与评估指标
对算法性能的测试与相关工作中所采用的实验方法保持一致,即使用干扰列表排序法.对于测试集中的每一个三元组(h,ri,t),枚举知识图谱中所有的实体,替换(h,ri,t)中的头实体,从中过滤掉已知的事实(即知识图谱中已有的三元组),得到第1组干扰事实列表,称为头干扰列表为
hlist={(h′,ri,t)|∀h′∈E∧(h′,ri,t)∉Δ},
(18)
类似地,构造尾干扰列表如下:
tlist={(h,ri,t′)|∀t′∈E∧(h,ri,t′)∉Δ}.
(19)
然后采用关系推理算法计算干扰列表中每个三元组的分值,并按照分值分别对头、尾干扰列表进行排序,取给定事实(h,ri,t)在相应排序结果中所处的位置作为评估关系推理结果的基础测度,分别记为rank(?,ri,t)和rank(h,ri,?).对二者求均值,得到关系推理算法对给定三元组的综合预测排名:
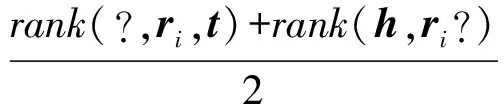
(20)
得到综合排名后,可进一步构造3种统计量对算法性能进行评估:首位命中率指标(hits@1)、前10命中率指标(hits@10)、平均倒数排名指标(mean reciprocal rank,MRR).hits@1定义如下:
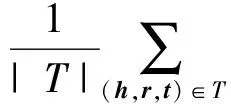
(21)
其中,符号T表示测试集,|T|表示测试集中的三元组个数.ind(·)为指示函数,定义:
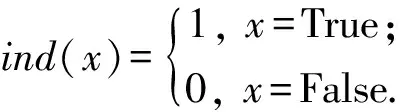
(22)
hits@1指标值表示排名第一的算法推理结果为正确知识的可能性,可以视为关系推理算法的准确率指标.类似地可以定义hits@10指标如下:
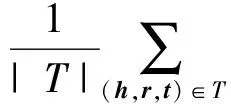
(23)
hits@10指标值表示正确结果出现在推理结果列表前10位(通常可接受的推荐列表长度)的概率,可以视为关系推理算法对知识的召回率指标.
进一步定义MRR指标的计算为
(24)
MRR指标表示对测试集中所有事实在推理结果列表中排名的倒数求平均值.由于给定事实在推理结果中的排名越靠前,其倒数值越大,因此MRR值越高,表明算法的推理性能也越好.但由于倒数取值范围是(0,1]区间,所以排名靠后的结果对MRR值的影响较大,因此MRR值能够全面反映算法的综合表现.
3.3实验结果与分析
本文所提出的UWM和IWM算法包含3个超参数需要在模型训练之前加以确定:SGD算法的学习率α、边界参数γ以及向量表达空间的维度k.
实验前采用网格搜索法(grid search)对上述参数进行选择.参考相关工作的实验参数,设定α的搜索范围为{0.01,0.005,0.001,0.000 5},γ的范围为{0.5,1.0,1.5,2.0},k的范围为{50,100,150,200}.在WN18和FB15k的验证集上分别进行网格搜索,取hits@10指标最优时的参数组合作为本文的实验参数:在WN18数据集上,参数取值为α=0.000 5,γ=1.0,k=50;在FB15k数据集上,参数取值为α=0.001,γ=1.5,k=150.在本文的所有实验中,SGD算法迭代次数统一设置为1 000轮.
3.3.1 算法性能综合评估
表4和表5分别给出了UWM和IWM算法与相关工作在WN18和FB15k这2个数据集上的实验对比情况.表中每列指标中性能表现最好的一项用粗体标出.由于TransE算法可以看作是UWM和IWM算法中权重向量的元素取值全为1的情况,因此可作为Baseline算法,用于评估本文基本假设的有效性.
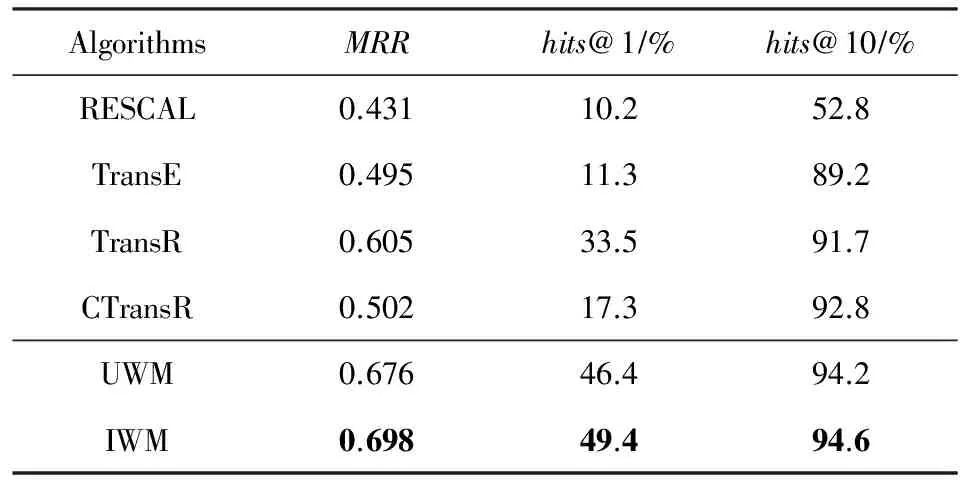
Table 4 Experimental Results on WN18 Dataset表4 WN18数据集上的实验结果
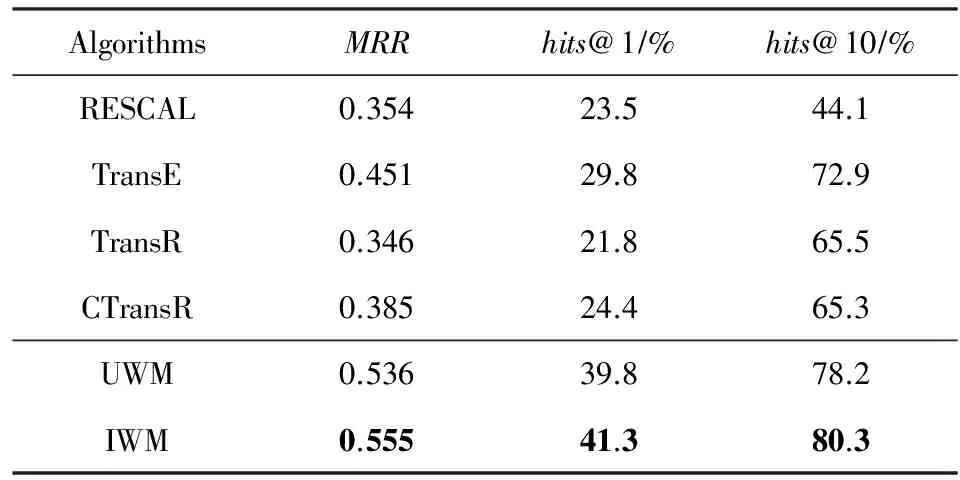
Table 5 Experimental Results on FB15k Dataset表5 FB15k数据集上的实验结果
由表4和表5可见,UWM算法和IWM算法在2个数据集的MRR和hits@1指标上的表现均一致且显著优于参与比较的相关算法.在WN18数据集上的hits@10指标表现与TransE,TransR和CTransR算法相当,在FB15k数据集上的hits@10指标则再次表现出显著优势.初步表明本文提出的假设和算法有效.
通过对比UWM算法和IWM算法的性能表现可以看出,IWM算法在2组实验中的所有性能指标上的表现均优于UWM算法,然而优势并不显著,除WN18数据集上的hits@1指标外,二者在其他性能指标上的差异小于5%.该结果表明,对同种类型关系两侧的实体向量分别进行加权处理,有助于提高关系推理算法的准确性和召回率.但由此带来的性能提升并不显著,意味着通过适当改进共享权重参数的估计方法,有可能达到同样的效果.
为深入揭示UWM和IWM算法的相对优势及其产生原因,接下来以IWM算法为代表,将其逐一与相关算法的实验结果进行比对.由于基于张量分解的RESCAL算法在2组实验中的表现显著低于其余相关工作,因此将其排除在讨论范围之外.此外,TransR算法和CtransR算法的设计思路相近,因此本文将其合并进行讨论.首先比较TransE和IWM算法.
如2.2节所述,TransE算法可以被视为IWM算法的特例,当IWM权重向量的所有元素均取值为1时,IWM算法退化为TransE算法.从实验结果来看,在WN18和FB15k数据集上,IWM算法的MRR指标与TransE算法相比分别提高了41.01%和23.06%,说明IWM中引入的权重处理机制显著地影响了正确结果(已知事实)在干扰列表中的分布,使之向列表的顶部偏移,从而进一步验证了本文假设的合理性,即知识图谱中的关系可以通过对其相关联的实体向量的方面要素进行选择性加权进行区分,通过合理建模,可以有效提升推理结果的准确率.
进一步对二者的准确率和召回率指标进行比对,可以看到在WN18和FB15k数据集上,IWM算法的hits@1指标与TransE算法相比分别提高了337.17%和38.60%;hits@10指标分别提高了6.05%和10.15%.该结果表明,新引入的假设能够对推理模型的准确率和召回率同时产生积极影响,但对于算法准确率的影响更为显著,说明该假设有助于提高表示学习模型对于同类型实体(出现在同种关系一侧的实体集合)的分辨率,由此进一步证明本文提出的假设是有效的.
将IWM算法与TransR和CtransR二者中表现较好的结果进行比较,可以看到在WN18和FB15k数据集上,IWM的MRR指标分别提高了15.37%和44.16%;hits@1指标分别提高了47.46%和69.26%.hits@10指标分别提高了1.94%和22.60%.该结果表明,与将实体和关系分别映射到不同语义空间的TransR和CtransR算法相比,IWM算法的鲁棒性更好,且对实体和关系语义差异的分辨能力更优.
综上,与相关工作相比,本文提出的UWM和IWM算法在关系推理准确率指标(hits@1)上的优势十分明显,在WN18和FB15k数据集上与性能最接近的算法相比,准确率提高水平也超过了38.60%.此外,IWM算法在上述数据集上的推理准确率分别达到49.4%和41.3%,意味着在一般关系推理任务,用户能够以近40%的把握接受算法给出的第一项推理结果,因此具备良好的实际应用前景.
3.3.2 在不同关系类型上的性能分析
为进一步分析UWM和IWM算法性能优势的成因,本文在FB15k数据集上做了关系分类实验.首先,将FB15k测试集按照式(11)划分成4类,然后分别对其进行关系推理实验,结果如表6和表7所示.为便于分析比较,相关工作选择了可被视为本文提出的算法特例的TransE算法和相关算法中综合性能表现最好的CtransR算法作为实验参考对象.

Table 6 Evaluation Results of hits@1 on FB15k Dataset

Table 7 Evaluation Results of hits@10 on FB15k Dataset
首先比较UWM和IWM算法的性能表现,可以看出在hits@1和hits@10指标上,二者在多数关系类型上的性能表现十分接近(差异小于5%),仅在处理M∶1类型关系的头干扰列表时表现出系统性差异,与UWM算法相比,IWM算法在hits@1指标上准确率高出14.15%,在hits@10指标上召回率高出6.30%.然而,考察与之相对应的1∶M类型关系尾干扰列表,可以看出IWM算法在上述2个指标上只分别高于UWM算法5.45%和1.64%.该结果表明,造成上述性能表现差异的原因可能与测试数据分布和训练数据量不足有关,并不足以证明IWM算法比UWM算法的性能更优,对此将在下一步工作中加以验证.
接下来考察本文提出的UWM和IWM算法与TransE和CtransR算法的性能对比.从表6可以看出,相对于另外2个参考算法,UWM和IWM算法在所有8个子项上的推理准确率表现都占据了明显的优势,尤其是在处理1∶M和M∶1关系类型时,准确率提升更为显著.该实验结果进一步表明本文提出的算法能够有效提升实体与关系的向量表达的准确性,从而提高实体分辨率,同时也间接说明本文提出的基本假设具有合理性,即可以通过对关系两侧的实体向量中包含的方面要素进行加权组合,获得对关系的向量表达.同样的情况也出现在表7的实验结果中,本文提出的2种算法,在4种关系类型的召回率指标上也全面占优,在处理1∶M和M∶1关系类型的优势更为显著.进一步验证了本文假设的有效性.
值得注意的是,尽管实验数据证明了UWM和IWM算法能够克服部分TransE基本假设存在的问题,提高算法对实体和关系语义的分辨能力,从而大幅提升关系推理准确率,但是从表6和表7的实验数据不难看出,UWM和IWM算法在处理1∶M和M∶1关系类型数据时,同样存在明显的性能不均衡性.例如,UWM算法在处理1∶M关系类型的头干扰列表时,hits@1准确率达到70.7%,但在处理M∶1类型的头干扰列表时,hits@1准确率只有20.5%.类似的情况在表6右侧的尾干扰列表,以及表7中均可以观察到.该结果表明,本文提出的建模假设仅揭示了部分客观规律,并没有完全解决TransE基本假设中存在的矛盾问题.然而,从实验结果所反馈的积极信号来看,本文的工作在一定程度上触及了问题的本质,为下一步工作提供了一个有希望的参考解决方案.
4 结束语
本文研究了知识图谱上的关系推理问题,指出了当前基于表示学习的关系推理模型所普遍采用的基本假设存在理论问题,并据此提出了新的建模假设和数学模型.在WN18和FB15k等基准数据集上的仿真实验表明,本文所提出的算法在所有指标上的性能表现一致且显著优于本领域的代表性工作,且算法计算效率高,可适用于大规模知识图谱关系推理任务.
该工作为研究基于表示学习的关系推理算法提供了新的建模思路和解决方案,同时也留下了一些值得继续研究的问题,比如:IWM所采用的独立加权方式是否优于UWM所采用的共享参数方式;本文提出的算法为什么在大幅提高1∶M和M∶1关系类型推理准确率的同时,却未能消除算法对关系两侧实体的推理能力的不均衡问题.在后续工作中,将针对上述问题开展进一步研究,目标是提出更为合理的关系推理建模思路和设计更为高效的推理算法.
[1] Nickel M, Murphy K, Tresp V, et al. A review of relational machine learning for knowledge graphs[J]. Proceedings of the IEEE, 2016, 104(1): 11-33
[2] Liu Qiao, Li Yang, Duan hong, et al. Knowledge graph construction techniques[J]. Journal of Computer Research and Development, 2016, 53(3): 582-600 (in Chinese)(刘峤, 李杨, 段宏, 等. 知识图谱构建技术综述[J]. 计算机研究与发展, 2016, 53(3): 582-600)
[3] Wang Yuanzhuo, Jia Yantao, Liu Dawei, et al. Open web knowledge aided information search and data mining[J]. Journal of Computer Research and Development, 2015, 52(2): 456-474 (in Chinese)(王元卓, 贾岩涛, 刘大伟, 等. 基于开放网络知识的信息检索与数据挖掘[J]. 计算机研究与发展, 2015. 52(2): 456-474)
[4] West R, Gabrilovich E, Murphy K, et al. Knowledge base completion via search-based question answering[C] //Proc of the 23rd Int World Wide Web Conf. New York: ACM, 2014: 515-526
[5] Liu zhiyuan, Sun Maosong, Lin Yankai, et al. Knowledge representation learning: A review[J]. Journal of Computer Research and Development, 2016, 53(2): 247-261 (in Chinese)(刘知远, 孙茂松, 林衍凯, 等. 知识表示学习研究进展[J]. 计算机研究与发展, 2016. 53(2): 247-261)
[6] Dong X, Gabrilovich E, Heitz G, et al. Knowledge vault: A Web-scale approach to probabilistic knowledge fusion[C] //Proc of the 20th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM. 2014: 601-610
[7] Liu Qiao, Jiang Liuyi, Han Minghao, et al. Hierarchical random walk inference in knowledge graphs[C] //Proc of the 39th Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2016: 445-454
[8] Getoor L, Mihalkova L. Learning statistical models from relational data[C] //Proc of the 2011 ACM SIGMOD Int Conf on Management of data. New York: ACM, 2011: 1195-1198
[9] Richardson M, Domingos P. Markov logic networks[J]. Machine Learning, 2006, 62(1): 107-136
[10] Friedman N, Getoor L, Koller D, et al. Learning probabilistic relational models[C] //Proc of IJCAI 1999. San Francisco, CA: Morgan Kaufmann, 1999: 1300-1309
[11] Schoenmackers S, Etzioni O, Weld D S, et al. Learning first-order horn clauses from web text[C] //Proc of the 2010 Conf on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2010: 1088-1098
[12] Lao Ni, Mitchell T, Cohen W W. Random walk inference and learning in a large scale knowledge base[C] //Proc of the 2011 Conf on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2011: 529-539
[13] Gardner M, Mitchell T. Efficient and expressive knowledge base completion using subgraph feature extraction[C] //Proc of the 2015 Conf on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2015: 1488-1498
[14] Pennington J, Socher R, Manning C D. GloVe: Global vectors for word representation[C] //Proc of the 2014 Conf on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2014: 1532-1543
[15] Mikolov T, Sutskever I, Chen Kai, et al. Distributed representations of words and phrases and their compositionality[C] //Proc of the 26th Int Conf on Neural Information Processing Systems. Cambridge, MA: MIT Press, 2013: 3111-3119
[16] Bordes A, Usunier N, Garcia-Duran A, et al. Translating embeddings for modeling multi-relational data[C] //Proc of the 27th Annual Conf on Neural Information Processing Systems. Cambridge, MA: MIT Press, 2013: 2787-2795
[17] Nickel M, Tresp V, Kriegel H-P. A three-way model for collective learning on multi-relational data[C] //Proc of the 28th Int Conf on Machine Learning. New York: ACM, 2011: 809-816
[18] Bordes A, Weston J, Collobert R, et al. Learning structured embeddings of knowledge bases[C] //Proc of the 25th AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2011
[19] Wang Zhen, Zhang Jianwen, Feng Jianlin, et al. Knowledge graph embedding by translating on hyperplanes[C] //Proc of the 28th AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2014: 1112-1119
[20] Fan Miao, Zhou Qiang, Chang Emily, et al. Transition-based knowledge graph embedding with relational mapping properties[C] //Proc of Pacific Asia Conf on Language, Information and Computation. Stroudsburg, PA: ACL, 2014: 328-337
[21] Lin Yankai, Liu Zhiyuan, Sun Maosong, et al. Learning entity and relation embeddings for knowledge graph completion[C] //Proc of the 29th AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2015: 2181-2187
[22] Socher R, Chen Danqi, Manning C D, et al. Reasoning with neural tensor networks for knowledge base completion[C] //Proc of the 27th Conf on Neural Information Processing Systems. Cambridge, MA: MIT Press, 2013: 926-934
[23] Lin Yankai, Liu Zhiyuan, Luan Hanbo, et al. Modeling Relation Paths for Representation Learning of Knowledge Bases[C] //Proc of the 2015 Conf on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2015: 705-714
RepresentationLearningBasedRelationalInferenceAlgorithmwithSemanticalAspectAwareness
Liu Qiao, Han Minghao, Yang Xiaohui, Liu Yao, and Wu Zufeng
(SchoolofInformationandSoftwareEngineering,UniversityofElectronicScienceandTechnologyofChina,Chengdu610054)
Knowledge representation based relational inference algorithms is a crucial research issue in the field of statistical relational learning and knowledge graph population in recent years. In this work, we perform a comparative study of the prevalent knowledge representation based reasoning models, with detailed discussion of the general potential problems contained in their basic assumptions. The major problem of these representation based relational inference models is that they often ignore the semantical diversity of entities and relations, which will cause the lack of semantic resolution to distinguish them, especially when there exists more than one type of relation between two given entities. This paper proposes a new assumption for relation reasoning in knowledge graphs, which claims that each of the relations between any entity pairs reflects the semantical connection of some specific attention aspects of the corresponding entities, and could be modeled by selectively weighting on the constituent of the embeddings to help alleviating the semantic resolution problem. A semantical aspect aware relational inference algorithm is proposed to solve the semantic resolution problem, in which a nonlinear transformation mechanism is introduced to capture the effects of the different semantic aspects of the embeddings. Experimental results on public datasets show that the proposed algorithms have superior semantic discrimination capability for complex relation types and their associated entities, which can effectively improve the accuracy of relational inference on knowledge graphs, and the proposed algorithm significantly outperforms the state-of-the-art approaches.
statistical relational learning; relational inference; representation learning; knowledge graphs; multi-relational data mining

Liu Qiao, born in 1974. PhD and associate professor. Member of CCF. His main research interests include machine learning and data mining, natural language processing, and social network analysis.

Han Minghao, born in 1992. Mater. Student member of CCF. His main research interests include natural language processing and machine learning (hanmhao@gmail.com).

Yang Xiaohui, born in 1993. Mater. Her main research interests include machine learning, natural language processing and data mining (yangxhui@std.uestc.edu.cn).

Liu Yao, born in 1978. PhD and Lecturer. Member of CCF. Her main research interests include social network analysis, machine learning, data mining, and network measurement (liuyao@uestc.edu.cn).

Wu Zufeng, born in 1978. PhD and Engineer. Member of CCF. His main research interests include machine learning, data mining, and information security (wuzufeng@uestc.edu.cn).
2017-03-20;
:2017-05-15
国家自然科学基金项目(61133016,U1401257);四川省高新技术及产业化面上项目(2017GZ0308) This work was supported by the National Natural Science Foundation of China (61133016,U1401257) and the General Program of the Sichuan Province High-Technology Industrialization (2017GZ0308).
TP391
