基于频响函数分析的主轴-刀柄-刀具结合面轴向分布参数辨识

朱坚民 何丹丹

上海理工大学机械工程学院，上海，200093

基于频响函数分析的主轴-刀柄-刀具结合面轴向分布参数辨识

朱坚民 何丹丹

上海理工大学机械工程学院，上海，200093

针对主轴-刀柄-刀具结合面轴向分布参数的精确辨识问题，提出了一种基于频响函数分析的主轴-刀柄、刀柄-刀具结合面建模及参数辨识的方法。该方法根据主轴系统中各零部件之间的连接关系，将轴承-主轴结合面简化为集中的弹性支撑，建立主轴-刀柄、刀柄-刀具结合面参数沿主轴轴向呈离散分布的结合面模型，并通过Cuckoo search算法辨识结合面参数，确定其在轴向上的分布情况。以4刃铣刀为例，基于所辨识的结合面参数，在ANSYS中建立主轴系统的动力学模型，计算刀尖点频响函数，并与实测值进行比较。结果表明：主轴-刀柄、刀柄-刀具结合面参数在轴向上呈现非线性分布，由其确定的刀尖点频响函数计算值和实测值之间的相对误差在4%以内，达到了较高的建模精度。

刀尖点频响函数；频响函数分析；结合面参数；轴向分布

0 引言

主轴系统刀尖点频响函数(frequencyresponsefunction，FRF)在研究铣削颤振稳定性、预测动态铣削力以及研究机床动态特性等方面具有重要作用，而主轴系统中存在较多的结合面，结合面建模的准确性对刀尖点FRF的预测具有重要影响[1]。

在主轴系统结合面的建模研究方面，目前常采用集中或均布的弹簧阻尼单元模拟结合面，如闫蓉等[2]以均布的弹簧阻尼单元模拟刀柄-刀具结合面，并采用遗传算法辨识结合面参数。王二化等[3]以集中的弹簧阻尼单元模拟主轴-刀柄-刀具结合面，利用传递矩阵法与响应耦合子结构分析(RCSA)法预测刀尖点FRF，并通过粒子群优化算法辨识结合面参数。XU等[4]以两对径向弹簧阻尼单元和一个轴向弹簧阻尼单元模拟主轴-刀柄的结合面。由于主轴、刀柄、刀具之间的结合面轴向长度较长，上述建模方法未准确反映主轴系统中结合面参数在轴向上的实际分布。为此，程强等[5]提出了基于FRF的主轴-刀柄结合部特征参数辨识方法，辨识了主轴-刀柄结合面在不同拉力作用下沿轴向不同位置处的刚度参数，但是该研究忽略了结合面的阻尼参数，且未考虑结合面模型中力矩对位移的耦合作用以及力对转角的耦合作用。BURNS等[6]认为，要准确预测刀尖点FRF，需建立考虑耦合作用的结合面模型。SCHMITZ等[7]和郑登升等[8]基于弹塑性理论和ANSYS仿真分析计算了HSK热装刀柄-刀具结合面沿轴向不同位置处的结合面参数，由于简化了结合面的模型，所辨识的结合面参数准确性不高。AHMADI等[9]提出刀柄-刀具结合面的连续弹性层模型，建立了刀柄-刀具结合面参数沿轴向变化的多项式方程，随后AHMADIAN等[10]采用类似原理建立了主轴-刀柄-刀具结合面的连续弹性层模型，但是由于假设结合面参数在主轴轴向上为线性分布，该研究仅从实验角度验证了假设的合理性，并未基于实验探究结合面参数在轴向上的实际分布情况。YANG等[11]提出一种适用于计算铣刀、镗刀以及钻头的刀尖点FRF的方法，建立了刀柄-刀具结合面的二次多项式模型，但未说明建立该模型的依据。综上，现有文献未建立完整的主轴系统结合面模型，即目前的文献或者忽略了轴承-主轴结合面，或者仅考虑主轴-刀柄-刀具中的部分结合面，而BUDAK等[12]认为主轴-轴承结合面影响主轴动态特性的刚体模态；SHAMEINE等[13]认为主轴刀尖点25%～50%的变形与主轴-刀柄-刀具结合面有关，因此已有文献辨识的结合面参数不能准确反映主轴系统中主轴-刀柄、刀柄-刀具的结合面参数在轴向上的实际分布情况。

针对上述问题，本文基于主轴系统的主轴、刀柄、刀具各个部件之间的频响函数分析，建立轴承-主轴、主轴-刀柄、刀柄-刀具的结合面模型，推导主轴-刀柄和刀柄-刀具的结合面参数在主轴轴向上的表达式，采用CuckooSearch优化算法辨识结合面的相关参数，研究主轴-刀柄-刀具结合面参数在轴向上的分布情况，并通过实验验证该模型的正确性。

1 主轴系统的结合面建模

主轴系统主要包含轴承、主轴、刀柄、刀具等零部件以及轴承-主轴、主轴-刀柄、刀柄-刀具等特性较为复杂的结合面，其中与主轴直接连接的轴承不仅起到支撑和定位作用，同时还提供足够的界面刚性，使主轴可承受一定的切削力[14]，主轴系统的典型结构如图1所示。本文根据主轴系统的实际结构，将其简化为多个子结构。对轴承-主轴结合面建模时，将其简化为弹性支撑；对主轴-刀柄-刀具结合面建模时，因主轴、刀柄、刀具三者之间结合面的接触长度较长，故将主轴-刀柄、刀柄-刀具结合面沿主轴轴向均匀设置若干个弹性支撑单元，各单元参数通过优化算法辨识确定。包含轴承-主轴、主轴-刀柄、刀柄-刀具结合面模型的主轴系统动力学模型如图2所示，图2中的数字表示子结构两端的节点，如节点1～节点2表示子结构①，节点2～节点3表示子结构②，以此类推。

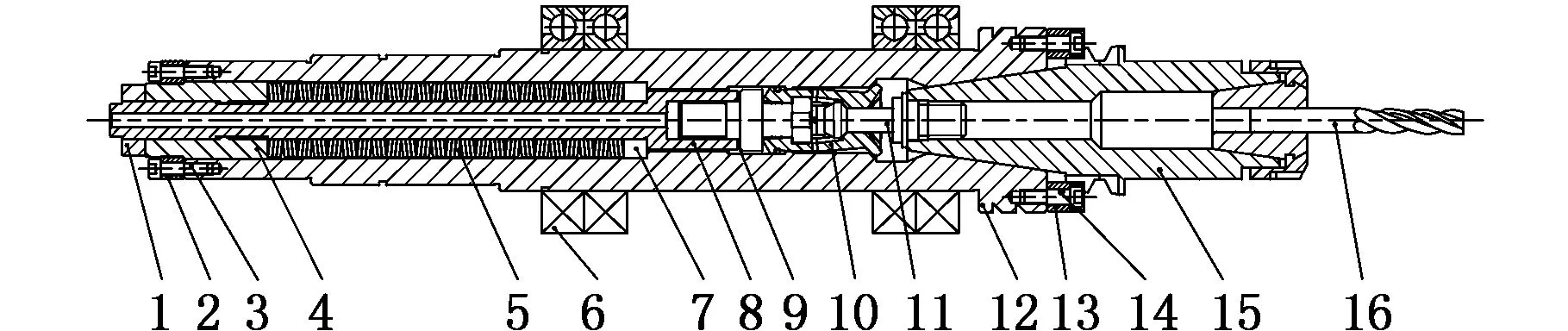
1.螺帽 2.压盖 3.内六角圆柱头螺栓M6 4.拉杆螺帽 5.盘形弹簧 6.角接触球轴承 7.拉杆垫圈 8.拉杆 9.安全华丝 10.四瓣爪 11.拉钉 12.主轴 13.主轴端键 14.内六角头圆柱螺栓M5 15.刀柄 16.铣刀图1 主轴系统的典型结构示意图Fig.1 Typical structure diagram of spindle system

图2 主轴系统动力学模型结构示意图Fig.2 Schematic of spindle system’s dynamic model

1.1 轴承-主轴结合面建模

在高速铣削加工中，轴承特性是影响铣削稳定性的主要因素之一，因此，在建立主轴系统的动力学模型时，轴承和主轴之间的结合面不可忽略。本文以VMC850E立式加工中心为研究对象，其主轴轴承为角接触球轴承，轴承刚度计算公式[15]如下：

(1)

式中，z为滚珠数量；D为滚珠直径；F为预紧力；α为轴承接触角。

经查相关技术资料，前后轴承的初始预紧力为69 kN，由式(1)可计算出轴承-主轴结合面刚度为1.734×1011N/m。

1.2 主轴-刀柄-刀具的结合面建模

根据结构动力学理论，对于自由度为n的主轴系统，其振动微分方程为

(2)

式中，X、M、C、K、F分别为主轴系统的位移矩阵、质量矩阵、阻尼矩阵、刚度矩阵以及受到的力载荷；ω为主轴系统的角频率。

由式(2)可得主轴系统的位移/力频响函数：

(3)

根据主轴系统所受的载荷(力矩载荷、力载荷)和计算的响应(位移响应、转角响应)之间的不同组合，可得到主轴系统的位移/力矩频响函数L、转角/力频响函数N以及转角/力矩频响函数P，如下所示：

(4)

式中，Mm为主轴系统受到的力矩载荷；θ为主轴系统在载荷作用下的转角。

为计算方便，本文在图2所示的主轴-刀柄、刀柄-刀具结合面沿着主轴轴向均匀设置相同数目的结合面单元。为表示方便，主轴-刀柄结合面之间的结合面单元编号采用Ⅰ,Ⅱ,…,m，如图3a所示。刀柄-刀具结合面之间的结合面单元编号采用1,2,…,n，如图3b所示。

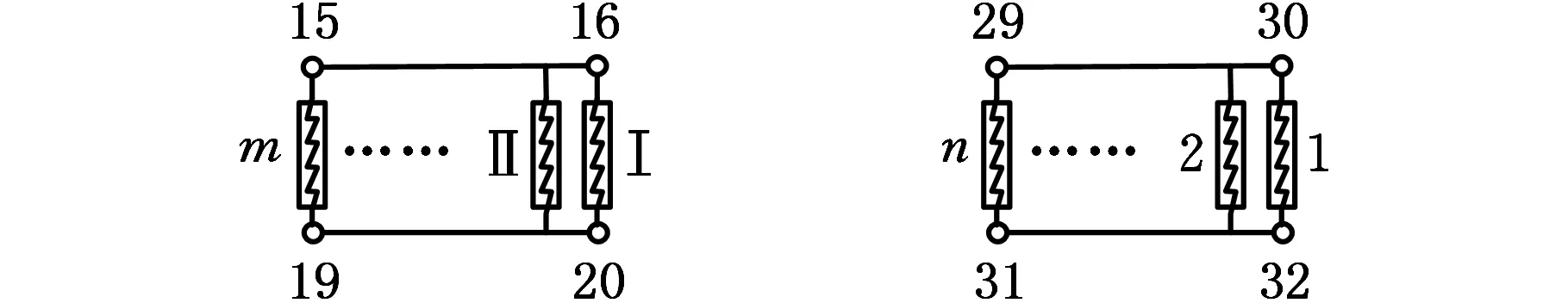
(a)主轴-刀柄结合面 (b)刀柄-刀具结合面图3 主轴-刀柄-刀具结合面轴向单元设置Fig.3 Units setup of interface among spindle-holder- tool on axis

根据图2中主轴、刀柄、刀具之间的连接关系，可得刀具上各点的响应、激励以及频响函数之间的关系：

(5)

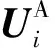
(6)

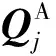
(7)

(8)

式中，Hij、Lij、Nij、Pij分别为刀具在j点激励作用下i点处获得响应的位移/力、位移/力矩、转角/力以及转角/力矩的频响函数，i,j=1, 2,…, n。

同理可得刀柄上各点的响应、激励以及频响函数之间的关系：

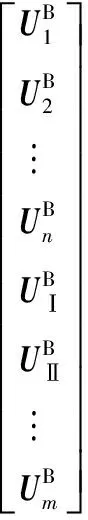
(9)

同理，主轴上各点的响应、激励以及频响函数之间的关系为

(10)

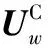
根据刀柄、刀具之间的连接关系，确定刀柄-刀具结合面的力平衡方程如下：

(11)

同理得到主轴-刀柄结合面的力平衡方程：

(12)

联立式(5)～式(12)，可得

(13)

(14)

式(14)中,K1,K2,…,Kn表示刀柄-刀具结合面沿着主轴轴向均匀设置的结合面参数，可表示为

(15)

i=1,2,…,n

式(14)中,KⅠ,KⅡ,…,Km表示主轴-刀柄结合面沿着主轴轴向均匀设置的结合面参数，可表示为

(16)

w=Ⅰ,Ⅱ,…,m

根据图2，由刀尖点的响应、激励以及刀尖点FRF之间的关系，可得

(17)

式中，Gee为刀尖点频响函数矩阵，可通过文献[16]中的方法计算得到。

联立式(11)、式(17)可得

(18)

联立式(13)～式(14)，可将式(18)化简为

(19)

2 主轴-刀柄-刀具结合面参数辨识

为辨识主轴-刀柄、刀柄-刀具结合面的参数，由式(19)可得

(20)

(21)

根据式(20)等号两边的矩阵对应项相等，可得

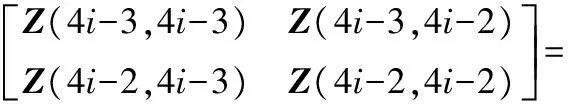
(22)

i=1,2,…,n

(23)

j=Ⅰ,Ⅱ,…,m

式(22)、式(23)分别表示式(20)左右两端任意位置处所对应的矩阵，具体的位置由i、j的具体取值确定。

为辨识刀柄-刀具和主轴-刀柄的结合面参数，本文采用Cuckoo Search优化算法进行辨识，Cuckoo Search算法[17]寻优效率高，待定参数少，且在解决复杂优化问题时一般不需要重新设置参数，相比遗传算法、粒子群算法等经典的启发式智能优化算法，该算法在解决很多优化问题上更胜一筹[18]。为求解刀柄-刀具结合面参数，建立如下目标函数：

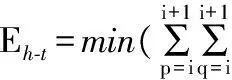
(24)

其中，Zcal(p,q)表示式(22)等号左边的表达式，Zcs(p,q)表示式(22)等号右边的表达式。

同理，为求解主轴-刀柄的结合面参数，建立如下目标函数：

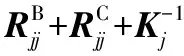
(25)

3 实验验证

为了验证本文方法的有效性，本文基于VMC850E立式加工中心，将型号为ER32-100L的刀柄BT40安装在主轴上，并将直径为10 mm的四刃铣刀安装在刀柄中，进行实验验证。

3.1 主轴系统的有限元模型

为辨识主轴-刀柄、刀柄-刀具中的结合面参数，需要先计算出各个部件的频响函数。本文将主轴、刀柄、刀具简化为Timoshenko梁模型，通过ANSYS中的谐响应分析法，计算各模型的频响函数。将主轴-刀柄、刀柄-刀具之间连接的部分分别等距划分为10段(即将图2中主轴上节点15～节点16之间等间隔划分为10个子结构，刀柄上节点19～节点20、节点29～节点30之间等间隔各划分为10个子结构，刀具上节点31～节点32之间等间隔划分为10个子结构)，即在主轴-刀柄、刀柄-刀具结合面沿轴向分别辨识10个结合面复刚度矩阵。主轴、刀柄、刀具各段的分段几何尺寸如表1～表3所示。

表1 主轴尺寸Tab.1 Dimension of spindle

3.2 实验测试

本文以常用的对称型4刃铣刀为例进行验证。按照图4将铣刀刀柄安装在VMC850E立式加工中心上，然后将BK 4525B型三向加速度传感器安装在刀具上，利用Kisler 9724A型激振力锤，通过LMS SCADAS Mobile205数据采集系统，进行模态锤击实验，采用LMS Test. Lab分析软件确定铣刀刀尖点FRF实测值的各阶固有频率。

4 结合面参数辨识结果及分析

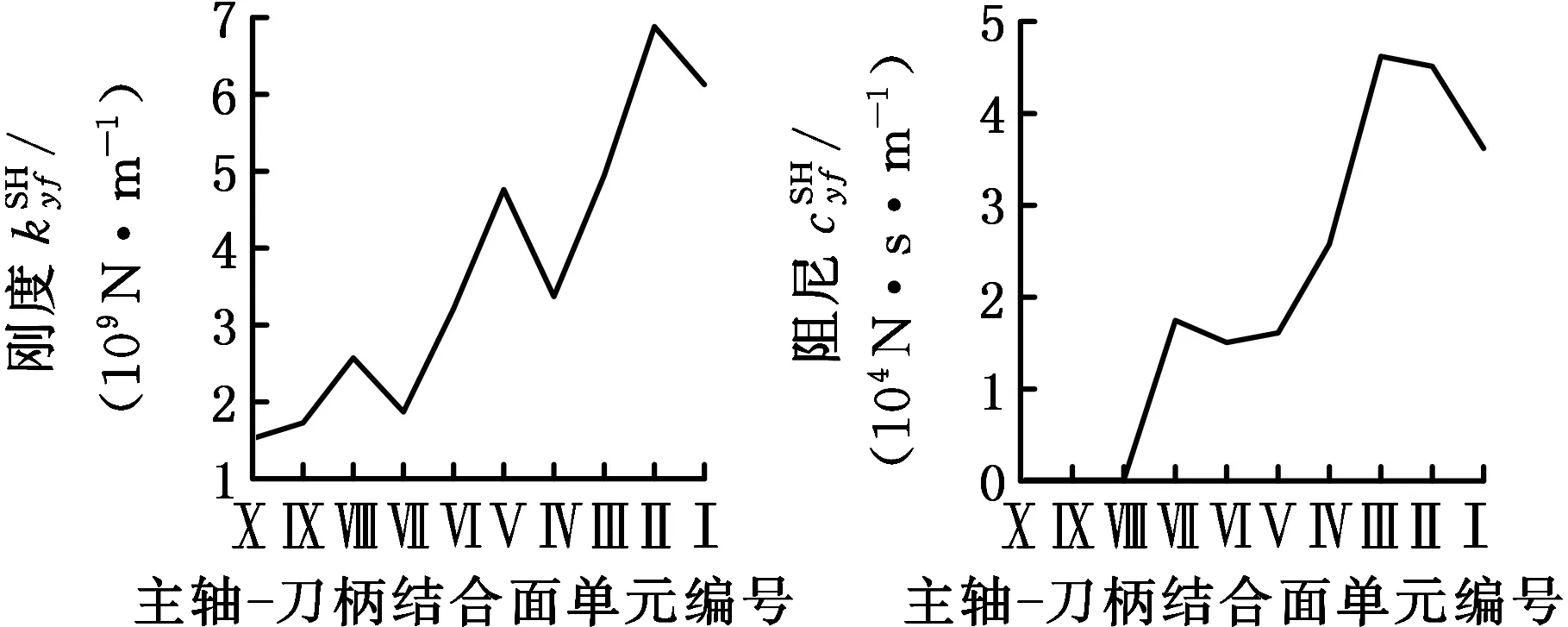
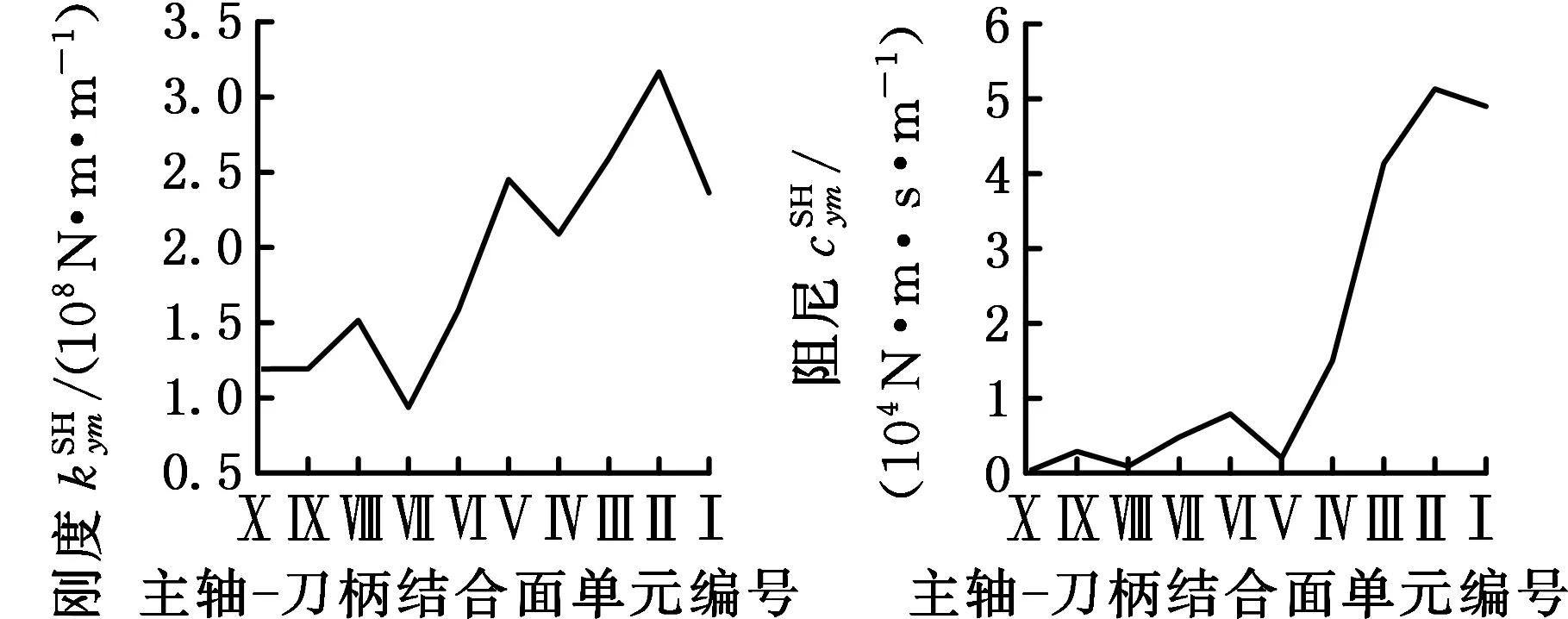
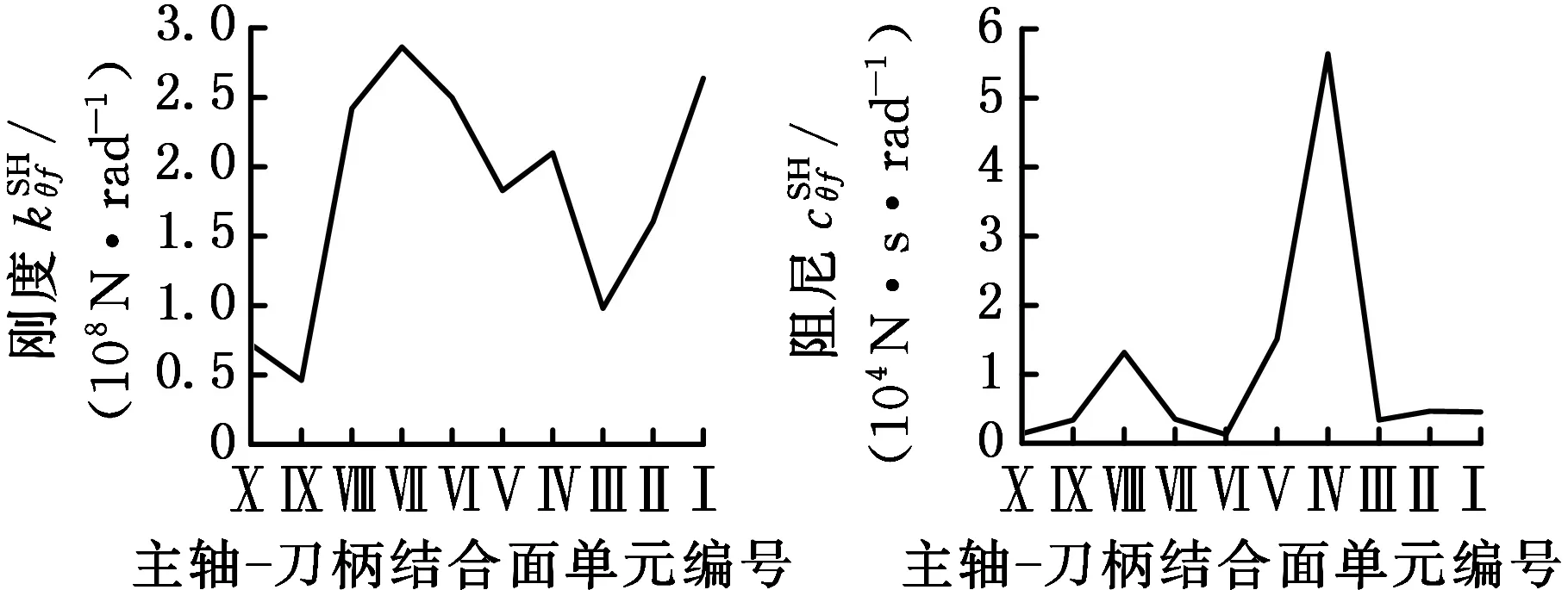
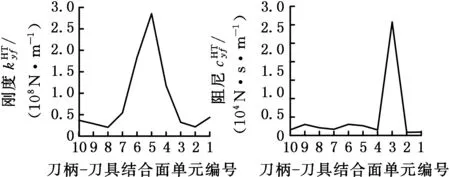
基于前述理论，辨识得到主轴-刀柄、刀柄-刀具的结合面参数，如图5、图6所示。

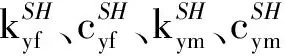
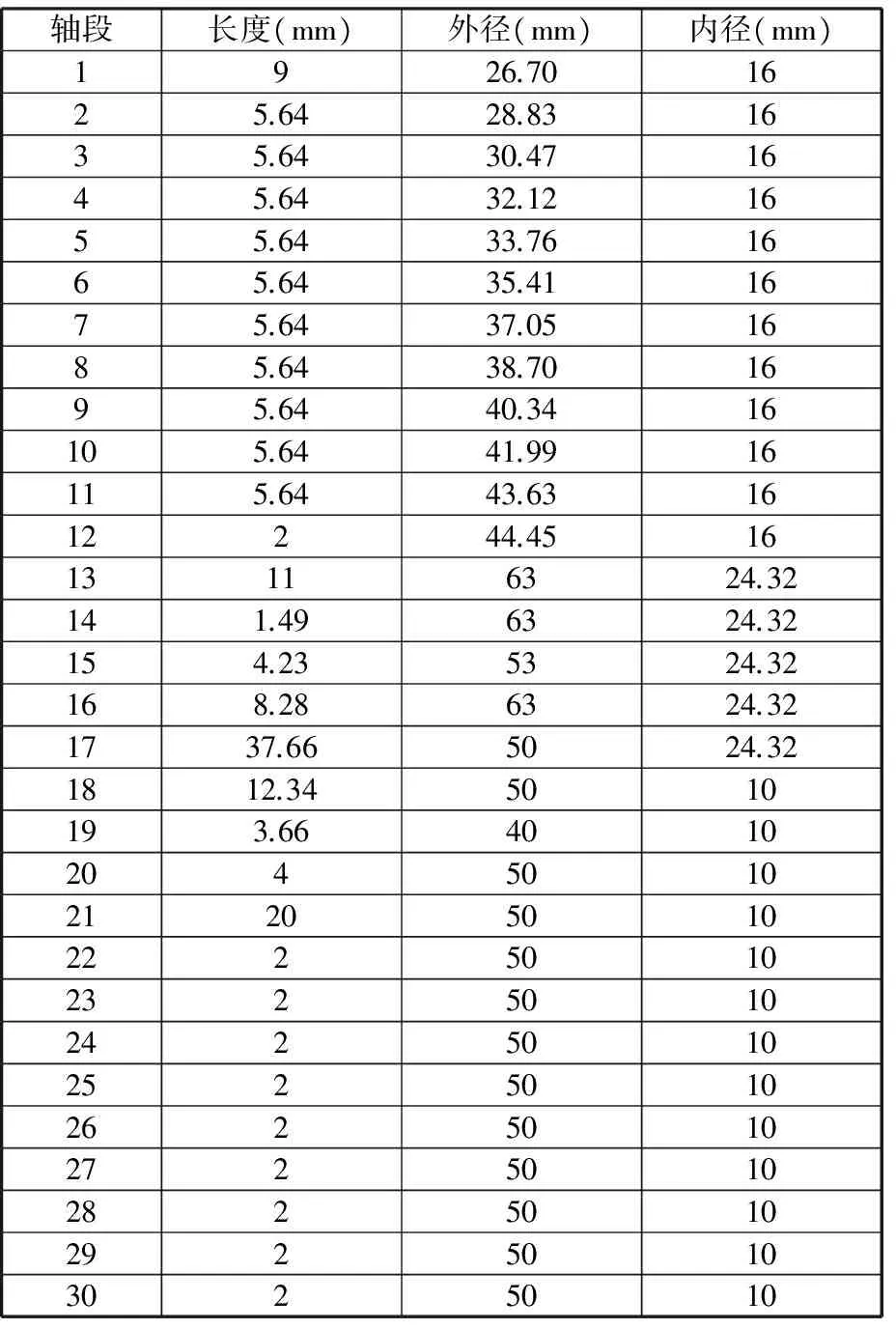
表2 刀柄尺寸Tab.2 Dimension of holder

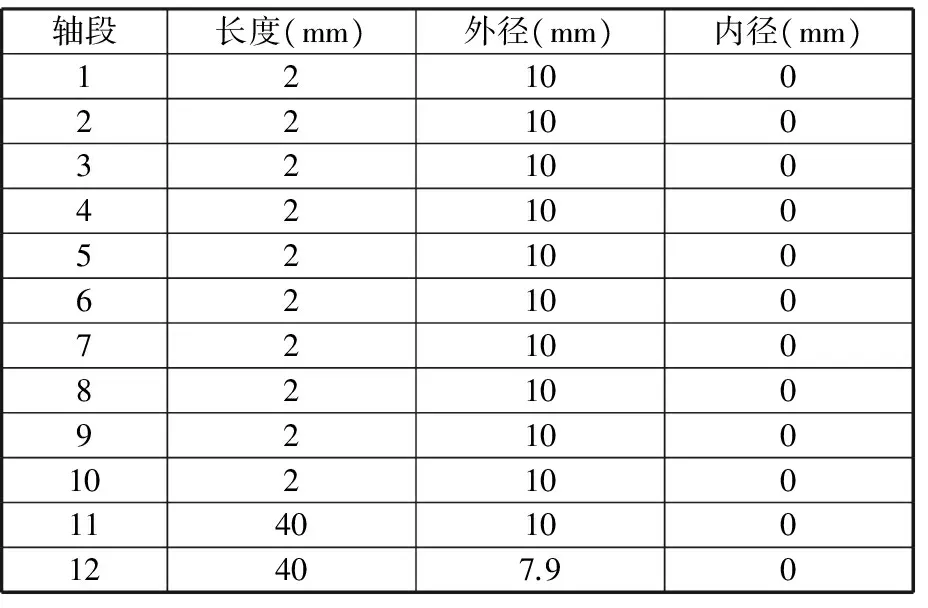
表3 刀具尺寸Tab.3 Dimension of tool

图4 铣刀刀尖点频响特性测试Fig.4 Tool point frequency response test

(a)主轴-刀柄结合面参数

(b)主轴-刀柄结合面参数

(c)主轴-刀柄结合面参数

(d) 主轴-刀柄结合面参数图5 主轴-刀柄结合面参数的辨识结果Fig.5 The spindle-holder contact parameters identified

(a)刀柄-刀具结合面参数

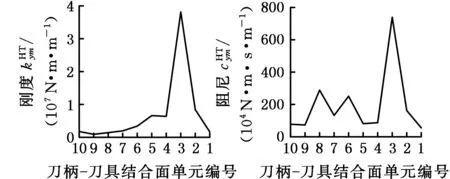
(b)刀柄-刀具结合面参数

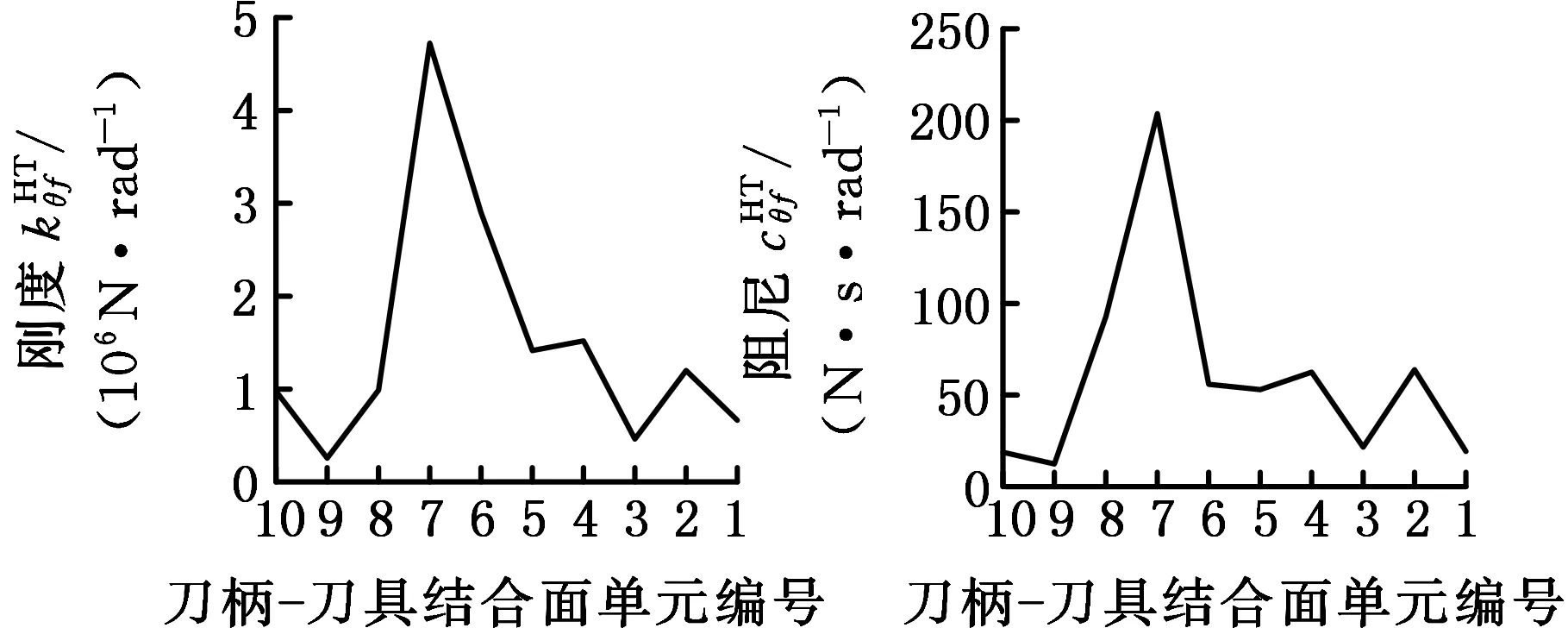
(c)刀柄-刀具结合面参数

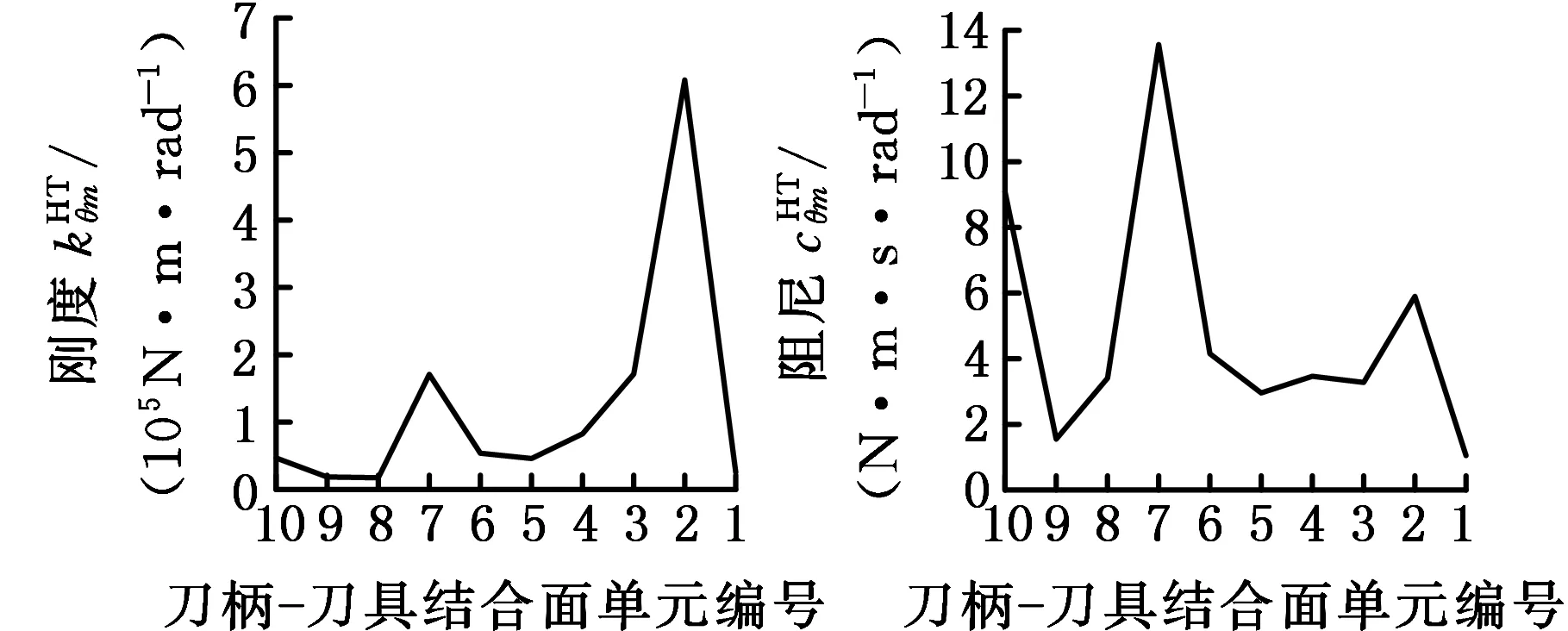
(d)刀柄-刀具结合面参数图6 刀柄-刀具结合面参数的辨识结果Fig.6 The holder-tool contact parameters identification

从图6中可以看出，刀柄-刀具结合面的8个参数呈现非线性，在刀柄-刀具结合面处出现峰值。因为实际切削过程中，主轴高速旋转，在离心力的作用下，连接刀具和刀柄的弹性夹头容易发生膨胀变形，而刀柄末端的圆螺母和刀柄之间为螺纹连接，加工过程中刀柄和刀具之间容易出现间隙，导致连接松动，使得该结合面处两端的刚度急剧下降，因此，在刀柄结构优化时，需要提高刀柄与刀具之间的配合精度，以满足高速切削时的刚度要求。

为验证上述辨识的结合面参数的准确性，本文在ANSYS中通过MATRIX27单元模拟轴承-主轴、主轴-刀柄以及刀柄-刀具结合面模型，并按图2的建模方法建立了VMC850E立式加工中心主轴系统的有限元模型，如图7所示。模型中的轴承-主轴结合面参数按照式(1)计算值进行设置，主轴-刀柄、刀柄-刀具的结合面轴向分布参数按图5、图6进行设置，其相应的材料参数如下：刀具的密度为14 133kg/m3，弹性模量为550GPa，泊松比为0.22;刀柄和主轴的密度为7870kg/m3，弹性模量为211GPa，泊松比为0.277，阻尼因子为0.003。然后通过谐响应分析可得到主轴系统刀尖点FRF的计算值。最后进行刀尖点FRF的测试实验与分析，并与计算值进行对比，结果如图8和表4所示。

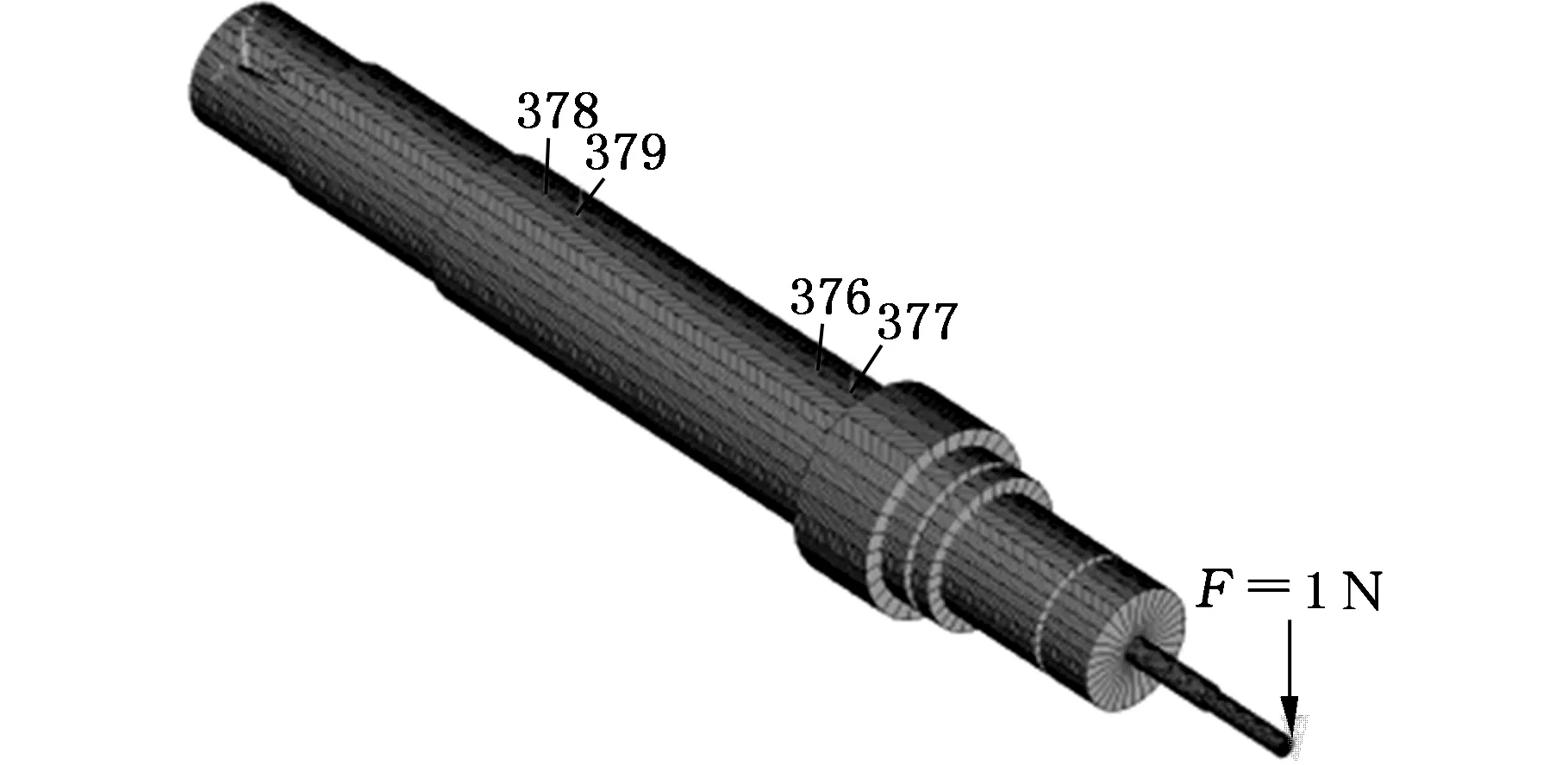
图7 主轴系统的有限元模型Fig.7 The finite element model of spindle system

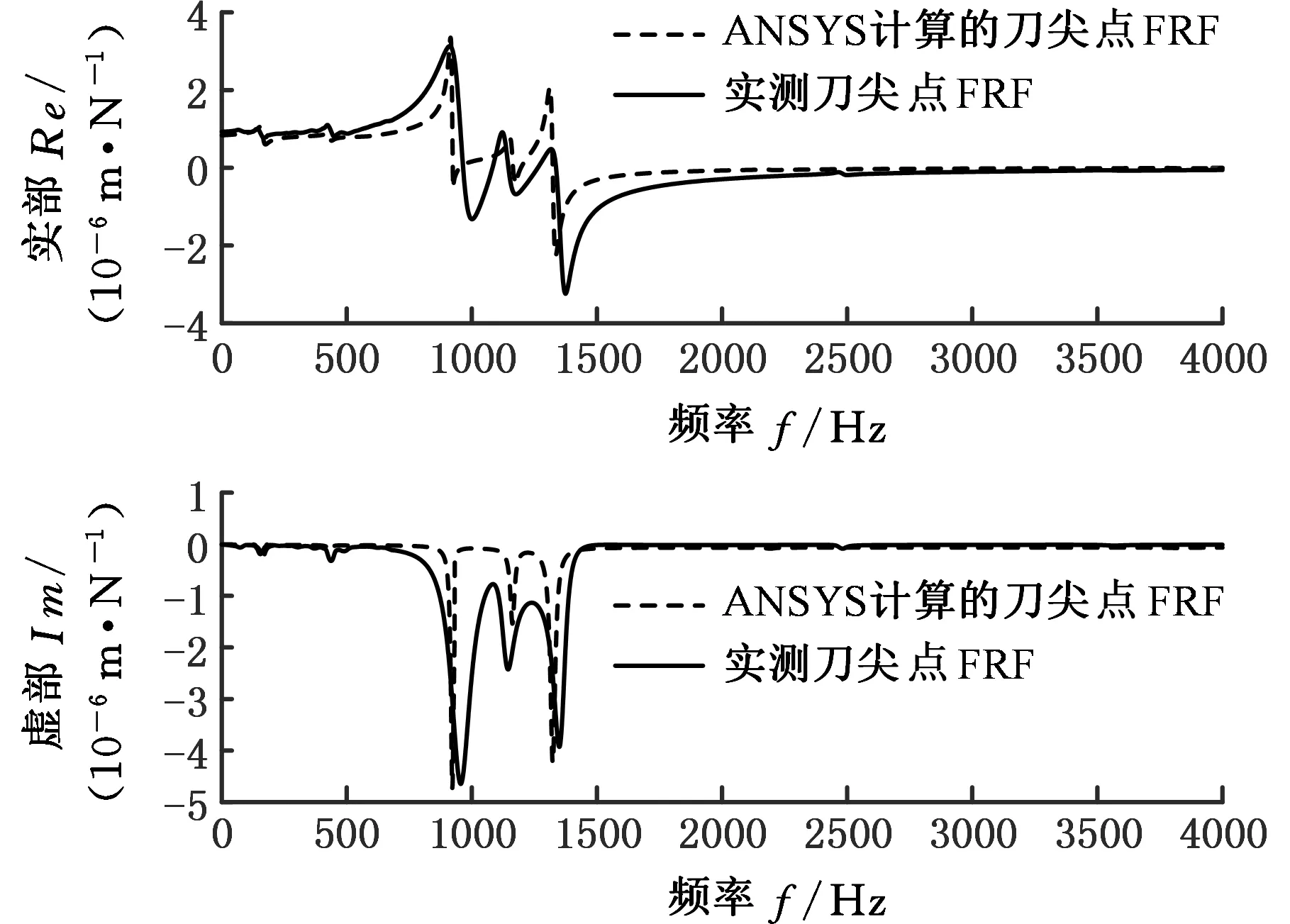
图8 刀尖点FRF的实测值与计算值的对比Fig.8 Comparison of tool point FRF measured with the calculated表4 刀尖点FRF固有频率的实测值与计算值对比Tab.4 Comparison of tool point FRF’s natural frequencies measured with the calculated

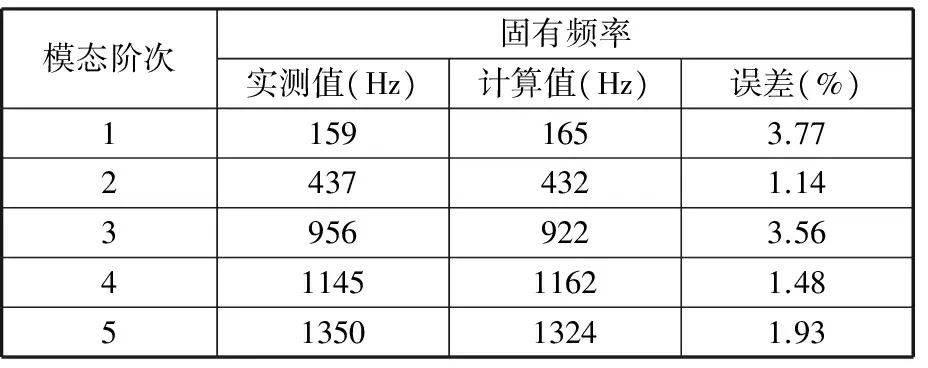
模态阶次固有频率实测值(Hz)计算值(Hz)误差(%)11591653．7724374321．1439569223．564114511621．485135013241．93

结合图8、表4可知，通过本文方法确定主轴-刀柄-刀具结合面参数，并据此计算的刀尖点FRF的固有频率理论值和实测值之间的误差在4%以内，说明本文方法的参数辨识精度较高。图8中两者之间的幅值在某些频率段内的差距较大，原因主要有：①ANSYS所建立的有限元模型是主轴系统的简化模型，存在一定的建模误差；②测量刀尖点FRF时，4刃铣刀和传感器之间的接触面积较小，存在一定的测量误差。尽管刀尖点FRF的实测值和理论值之间有一定差异，但是基于本文结合面参数辨识方法所预测的刀尖点FRF固有频率和实测值差异较小。因此，本文方法是有效的，并且通过本文方法可以进一步探究主轴-刀柄、刀柄-刀具结合面参数在轴向上的分布规律。

本文还以非对称型2刃铣刀为例，对VMC850E立式加工中心主轴系统中的主轴-刀柄、刀柄-刀具的结合面参数进行了建模、参数辨识、实验验证，结果表明：主轴-刀柄、刀柄-刀具结合面的轴向分布参数呈现非线性，并且多处出现峰值；由本文方法计算的刀尖点FRF的固有频率理论值和实测值之间的误差不超过2%。由于本文篇幅所限，未给出具体的实验结果与分析。

5 结论

(1)提出一种基于频响函数分析的主轴-刀柄、刀柄-刀具结合面建模及参数辨识方法，并考虑了轴承-主轴结合面的建模，根据主轴、刀柄、刀具之间的连接关系，推导出主轴-刀柄、刀柄-刀具结合面参数的辨识公式，基于Cuckoo Search优化算法辨识这些参数，获得了主轴-刀柄、刀柄-刀具结合面参数在主轴轴向上的分布。

(2)以4刃铣刀为例，基于所辨识的主轴系统结合面参数，在ANSYS中建立了主轴系统的动力学模型，基于谐响应分析法计算出刀尖点FRF，并和实测刀尖点FRF进行对比，结果表明基于本文方法建立的主轴系统动力学模型预测的刀尖点FRF的固有频率和实测值的误差在4%之内，达到了较高的预测精度。同时实验结果表明主轴-刀柄、刀柄-刀具结合面参数在主轴轴向上呈现非线性分布，为探究主轴-刀柄-刀具结合面建模提供了一定的理论支持。

[1] 汪博, 孙伟, 太兴宇, 等. 主轴系统结合面对主轴系统动力学特性的影响分析[J]. 振动与冲击, 2011, 30(10): 231-235. WANG Bo, SUN Wei, TAI Xingyu, et al. Effect of Interfaces on Dynamic Characteristics of a Spindle System[J]. Journal of Vibration and Shock, 2011, 30(10): 231-235.

[2] 闫蓉, 蔡飞飞, 彭芳瑜, 等. 基于响应耦合方法的铣刀刀尖点频响函数预测[J]. 华中科技大学学报(自然科学版), 2013, 41(4): 1-5. YAN Rong, CAI Feifei, PENG Fangyu, et al. Predicting Frequency Response Function for Tool Point of Milling Cutters Using Receptance Coupling[J]. Huazhong University of Science & Technology (Natural Science Edition), 2013, 41(4): 1-5.

[3] 王二化, 吴波, 胡友民, 等. 主轴-刀柄与刀柄-刀具结合面参数辨识研究[J]. 振动与冲击, 2014, 33(10): 50-54. WANG Erhua, WU Bo, HU Youmin, et al. Identification of Spindle-Holder and Holder-Tool Joint Parameters[J]. Journal of Vibration and Shock， 2014, 33(10): 50-54.

[4] XU C, ZHANG J J, WU Z J, et al. Dynamic Modeling and Parameters Identification of a Spindle-Holder Taper Joint[J]. International Journal of Advanced Manufacturing Technology, 2013, 67(5/8): 1517-1525.

[5] 程强, 刘新宇, 赵永胜, 等. 基于频响函数的主轴-刀柄结合部参数辨识方法[J]. 北京工业大学学报, 2013, 39(8): 1144-1148. CHENG Qiang, LIU Xinyu, ZHAO Yongsheng, et al. Identification of Dynamical Contact Parameters for Spindle-Tool Holder Interface Based on Frequency Response Functions[J]. Journal of Beijing University of Technology, 2013, 39(8): 1144-1148.

[6] BURNS T J, SCHMITZ T L. A Study of Linear Joint and Tool Models in Spindle-Holder-Tool Receptance Coupling[C]// International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Long Beach, California: American Society of Mechanical Engineers, 2005: 947-954.

[7] SCHMITZ T L, POWELL K, WON D, et al. Shrink Fit Tool Holder Connection Stiffness/Damping Modeling for Frequency Response Prediction in Milling[J]. International Journal of Machine Tools and Manufacture, 2007, 47(9): 1368-1380.

[8] 郑登升, 陈建, 陶德飞, 等. 高速HSK热装工具系统结合部的参数辨识[J]. 中国机械工程, 2015, 26(18): 2486-2490. ZHENG Dengsheng, CHEN Jian, TAO Defei, et al. Parameter Identification of High-speed HSK Shrink Tooling System Coupling Portion[J]. China Mechanical Engineering, 2015, 26(18): 2486-2490.

[9] AHMADI K, AHMADIAN H. Modelling Machine Tool Dynamics Using a Distributed Parameter Tool-Holder Joint Interface[J]. International Journal of Machine Tools and Manufacture, 2007, 47(12/13): 1916-1928.

[10] AHMADIAN H, NOURMOHAMMADI M. Tool Point Dynamics Prediction by a Three-component Model Utilizing Distributed Joint Interfaces[J]. International Journal of Machine Tools and Manufacture, 2010, 50: 998-1005.

[11] YANG Y, ZHANG W H, MA Y C, et al. Generalized Method for the Analysis of Bending, Torsional and Axial Receptances of Tool-Holder-Spindle Assembly[J]. International Journal of Machine Tools and Manufacture, 2015, 99: 48-67.

[12] BUDAK E, ERTÜRK A, ÖZGÜVEN H N. A Modeling Approach for Analysis and Improvement of Spindle-Holder-Tool Assembly Dynamics[J]. CIRP Annals—Manufacturing Technology, 2006, 55(1): 369-372.

[13] SHAMEINE D M, SHIN Y C. Analysis of No. 50 Taper Joint Stiffness under Axial and Radial Loading[J]. Journal of Manufacturing Processes, 2000, 2(3): 167-173.

[14] 刘玉. 高速机床主轴单元的动态特性分析及结构优化[D]. 西宁: 青海大学, 2009. LIU Yu. Dynamic Analysis and Structural Optimization of the High Speed Machine Tool’s Spindle Unit[D]. Xining: Qinghai University, 2009.

[15] 高相胜, 张以都, 张洪伟. 主轴-刀柄结合面刚度建模方法[J]. 计算机集成制造系统, 2013, 19(1): 61-66. GAO Xiangsheng, ZHANG Yidu, ZHANG Hongwei. Modeling Approach for Interface Stiffness of Spindle-Tool Holder[J]. Computer Integrated Manufacturing Systems, 2013, 19(1): 61-66.

[16] 朱坚民, 何丹丹, 田丰庆, 等. 一种新的预测铣刀刀尖点频响函数的方法[J]. 中国机械工程, 2016, 27(20): 2765-2773. ZHU Jianmin, HE Dandan, TIAN Fengqing, et al. A New Prediction Method of Tool Point Frequency Response Function for Milling Cutters[J]. China Mechanical Engineering, 2016, 27(20): 2765-2773.

[17] YANG X S, DEB S. Cuckoo Search via Lévy Flights[C] // Proceedings of World Congress on Nature and Biologically Inspried Computing. Coimbatore, 2009: 210-214.

[18] 赵玉新, (英)杨新社, 刘利强. 新兴元启发式优化算法[M]. 北京: 科学出版社, 2013: 173-200. ZHAO Yuxin, YANG Xinshe, LIU Liqiang. Emerging Heuristic Optimization Algorithms[M]. Beijing : Science Press, 2013: 173-200.

(编辑 王旻玥)

Identification of Axial Distribution Joint Parameters of Interfaces among Spindle-Holder-ToolBased on Frequency Response Function Analysis

ZHU Jianmin HE Dandan

School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai,200093

In allusion to identify the joint parameters for axial distribution interfaces among spindle-holder-tool accurately, a method of surface modeling and parameter identification of spindle-holder and holder-tool was proposed based on frequency response function analysis. According to the connection relationships among the various parts of spindle system, the bearing-spindle interfaces were simplified as some elastic supports and a discrete distribution model of interfaces among spindle-holder-tool was built on axial, and the corresponding contact parameters were identified through Cuckoo search algorithm, so as to explore their distributions. A four fluted milling cutter was used as an example, a spindle system’s dynamics model was established in ANSYS based on parameters identified, and the calculated tool point frequency response function in ANSYS was compared with the measured ones. Experimental results show a non-linear distribution of joint parameters for interfaces among spindle-holder-tool on axial, and the relative errors between the calculated tool point frequency response function and the measured ones are within 4%, which reaches a high prediction precision.

tool point frequency response function； frequency response function analysis； joint parameters； axial distribution

2017-03-13

国家自然科学基金资助项目(50975179)；上海市教委科研创新项目(11ZZ136)；上海市科委科研计划资助项目(12DZ2252300)

TH113

10.3969/j.issn.1004-132X.2017.16.001

朱坚民，男，1968年生。上海理工大学机械工程学院教授、博士研究生导师。主要研究方向为精密测试技术、机电系统的智能测控。E-mail：jmzhu@usst.edu.cn。何丹丹，女，1992年生。上海理工大学机械工程学院硕士研究生。