一种基于链接和语义关联的知识图示化方法

杨 林 张立波, 罗铁坚 万启阳 武延军

1(中国科学院大学 北京 101408) 2 (中国科学院软件研究所 北京 100190) (icode@iscas.ac.cn)

一种基于链接和语义关联的知识图示化方法

杨 林1张立波1,2罗铁坚1万启阳1武延军2

1(中国科学院大学 北京 101408)2(中国科学院软件研究所 北京 100190) (icode@iscas.ac.cn)

将海量的知识梳理成人类更容易接受的形式，一直是数据分析领域的难题.大多数传统分析方式直接对知识本身进行总结和描述概念化(conceptualization)；而一些教育实践证明，从临近的知识单元进行刻画图示化(schematization)更容易使一个知识点被人类接受.在目前的经典计算机知识表达方法中，知识图示化主要依靠人工整理完成.提出了一种利用计算机自动化完成知识图示化的方法，依托维基百科概念拓扑图，探究概念与其临近概念的关系，并且提出了基于链接的自动筛选最关联概念算法；使用目前最新的神经网络模型Word2Vec对概念间的语义相似度进行量化，进一步改进关联概念算法，提高知识图示化效果.实验结果表明：基于链接的关联概念算法取得了良好的准确率，Word2Vec模型可以有效提高关联概念的排序效果.提出的方法能够准确有效地主动分析知识结构，梳理知识脉络，为科研工作者和学习者提供切实有效的建议.

知识图示化；概念拓扑图；词嵌入；知识表达；维基百科

在人类知识库越来越庞大、分类越来越细化和专业化的今天，个体早已无法完全掌握人类的所有知识.人们自然而然地想到使用计算机来处理、存储和利用海量的知识.一方面，人们希望生产出能够充分利用人类知识库为自己服务的机器，继而产生了人工智能领域；另一方面，人类试图探究如何利用计算机完成对庞大知识数据的梳理和挖掘，用以提高人类的教育水平.无论以上哪个方面，都绕不开一个重要问题——如何用计算机对人类知识进行表示？人工智能领域的知识表示更倾向于对知识结构的描述，如逻辑表示、框架表示、本体表示[1]等，这些工作着眼于创造计算机能够接受的用于描述知识的数据结构.而用于教育人类自身的计算机知识大数据表示方式则更加直接，通常以“将知识梳理成人类更容易接受的形式”为核心目的，探究知识体系的表现形式.

很多实践证明，通过相关知识单元来描述给定知识点的知识表示方式更易被人类接受(例如思维导图Mind Map的蓬勃发展)，我们称之为知识的图示化(schematization)[2].在传统的教育方式中，由于人类教育者无法考虑到知识体系整体，只能着眼于对某个知识点本身的刻画，我们称之为知识的概念化(conceptualization)[3]；即使在教育过程中使用了相关知识点间的联系，这些联系本身也大多由经验丰富的人类教育者决定，缺乏普适性和客观性.而计算机的优势在于能够处理海量的数据，可以弥补人类教育者对于知识掌控的不足，本文将深入研究如何使用计算机对知识点进行合理、客观的图示化表示.

本文的主要贡献有3方面：1)通过建立维基百科概念拓扑图(Wikipedia concept topology, WCT)，并对其拓扑结构进行分析，提出了一种基于链接的概念相关性算法.2)运用自然语言处理中的分布式语义向量方法计算概念间的语义相似度并与基于链接的概念相关性算法结合，最终提出一种主动分析知识点并进行图示化表述的方法；3)提出了依靠知识的网络结构对概念进行分层、分类的思路，对计算机语义分析具有重要意义.

1 相关工作

在人类知识的整个结构框架中，概念是最重要的基本知识单元，而对于各种概念相关性的构建和量化是知识图示化的重要手段.对于概念相关性的计算主要依靠推荐系统和自然语言处理中的相关算法.目前主流的推荐算法主要有基于内容的推荐[4]、协同过滤推荐[5]、基于规则的推荐[6]等，而现有的推荐算法大多应用于社交网络，鲜见应用于知识网络中，本文尝试将推荐系统中的相似度算法推广到概念相关性计算中.

前人关于维基百科中的概念相关性算法有基于概念向量的方法、基于路径的方法、基于概率的方法和基于链接的方法等.基于向量的经典方法有Gabrilovich和Markovitch提出的精确语义分析(explicit semantic analysis)[7]，通过比较2篇文章中较重要概念组成的权重向量(weighted vector)判断它们的相关性；以及Shirakawa等人提出的概念向量(concept vector)[8]，通过比较2个概念投射到的对应分类组成的向量判断相关性.Strube和Ponzetto提出的基于路径的度量方式(path based measures)[9]，将概念投射到对应分类后比较分类中的最短路径.基于概率的方法依据模拟人类点击的概率分布(即概念的重要性)来判断相关性大小，例如Yeh等人提出的随机行走算法(random walks)[10]和Dallmann等人[11]提出的另一种随机行走算法的改进算法等.基于链接的方法是依靠概念网络中的链接来进行距离测算，如Milne和Witten提出的标准化链接距离(normalized link distance)和链接向量相似度(link vector similarity)[12].

虽然计算概念相关性的算法多种多样[11,13-15]，但这些算法大多适用于中远距离的概念，即区别较大的概念；而本文中需要比较的概念大多属于同一类别，于是我们提出了一种新的基于链接的相关性算法来判断概念的相关性，具体将在2.4节中叙述.

另外，在考虑概念相关性时自然会考虑到概念语义之间的相关性.自然语言处理领域关于语义关联的研究表明，词汇可以通过由神经网络训练的分布式语义向量表示，即词嵌入(Word Embedding)[16].Word Embedding是词项在低维空间中的语义向量表示，可用于度量概念间的语义关联.本文尝试利用一种词嵌入模型Word2Vec[16]来量化概念间的语义相似度，进而提高纯粹基于链接方法在计算相关概念方面的准确率和覆盖率.

2 知识图示化模型

2.1数据集与预处理

互联网百科全书是当前能够随意查阅的最大、最完整的人类知识库，其中维基百科是各国共同参与编撰的规模最大的互联网多语言百科全书，其与专业人士编撰的大英百科全书具有相近的正确率[17]，但由于编辑自由，发展更加迅速.截至2016年7月25日，英文维基百科总计拥有5 201 640篇文章、39 827 021个页面，覆盖了人类的大部分知识领域.其以词条为最小知识单元，以链接跳转表现知识之间的联系，具有紧密的结构以及普遍连通性，与人类思维模式高度一致，因此本文选取维基百科作为基本数据集.我们使用维基百科2016年6月1日发布的XML格式离线数据包作为原始数据，解压后的XML文件大小为53.4 GB，其中包含维基百科2016年6月以前的所有页面文本和超链接数据.

人类的知识是由一个个知识点(knowledge point)和它们之间的关系构成，概念是知识点的最小单位，维基百科数据集中概念的表达方式就是词条(title)[18].知识体系中，每个概念的刻画都由2个部分组成:1)概念本身包含的信息;2)与其他不同概念之间的关系.对应到维基百科的词条，就是词条本身的内容描述和与其他词条的链接关联.所以为了对概念之间的关系进行分析，我们不仅需要对维基百科的概念建立网络拓扑图，还需要对每个词条对应的文本进行语义分析.于是，我们对XML数据进行5步处理：

1) 抽取每个页面的文本信息(包括词条和词条的描述)和页面全部的链接；

2) 删除其中的非内容页(如分类页、帮助页等等)和空指向页，并且将所有重定向页与其指向的页面合并；

3) 将每个词条的首字母改为大写(统一命名规范)，并与其文本进行对应；获得维基百科内容语料数据集

4) 为了建立拓扑图，将单向链接变为双向链接，于是维基百科中的词条和链接就可以分别看成一个有向图的顶点和边的集合；

5) 利用广度优先搜索计算图的联通分量分布，去掉部分无关分量，获得维基百科拓扑图.

第5步处理获得的连通分量分布如表1所示，其中最大连通分量包含了维基百科中99.9%以上的词条，表明维基百科中的概念和知识网络具有普遍连通性的特点.其他连通分量中多为特殊字符等无关紧要的内容，因此我们将其忽略掉.将最大连通分量的12 269 222个词条连同它们之间的链接作为我们的概念拓扑图，其对应的概念和超链接作为我们研究的数据集.

最终我们获得了2个数据集：维基百科内容语料数据(content data of Wikipedia, CDW)和维基百科概念拓扑图(WCT).前者包含12 269 222个词条和这些词条对应的内容.后者包含了有向图GD(V,E)和对应的无向图GU(V,E)，其中V为所有概念对应的顶点(vertices)的集合，E为所有链接对应的有向边或无向边的集合.

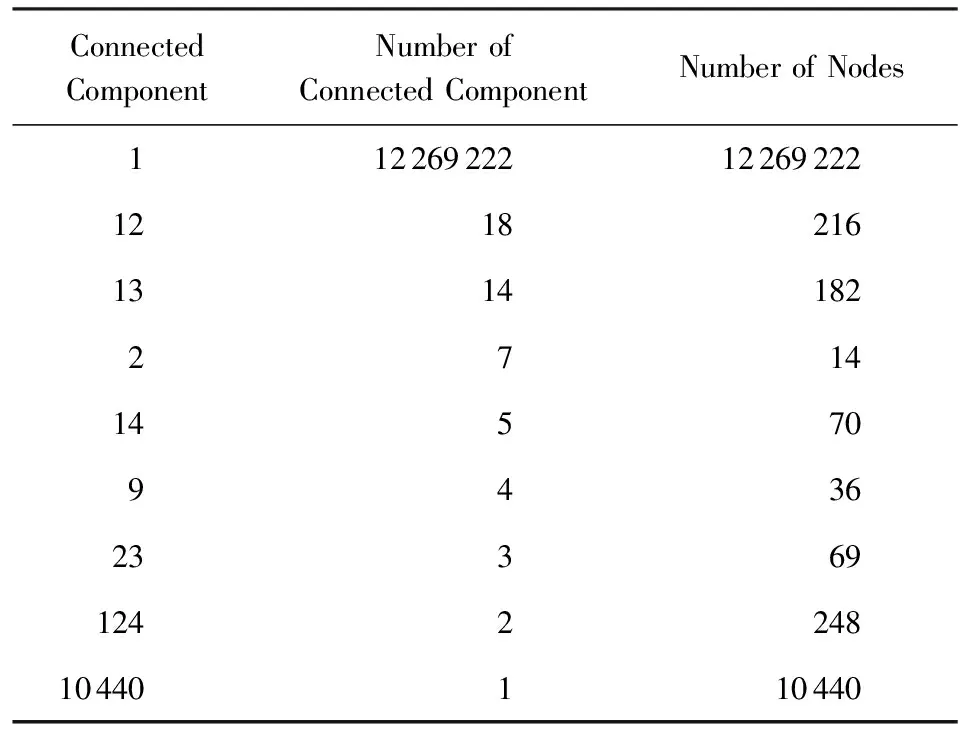
Table 1 Distribution of Connected Components表1 连通分量分布[19]

2.2概念相关性

从人类通常的思维方式出发，在接受一个未知的概念时，人们通常会利用与它相关的概念进行辅助理解.值得注意的是，这里的相关性概念不单包括简单意义上的“相近”，也包括从其他维度上的相关性.以单词记忆这种知识获取方式为例，原始的死记硬背方法效率十分低下.教育领域的相关研究发现：包括词根记忆、近反义词记忆、同领域单词记忆在内的各种维度的相关词记忆，都可以大大提高学习效果，即人们往往对一系列相关单词的记忆更加深刻(如图1所示).所以依据概念的相关性建立知识图谱，更加符合人类的思维方式，也更利于提高知识理解的效率.

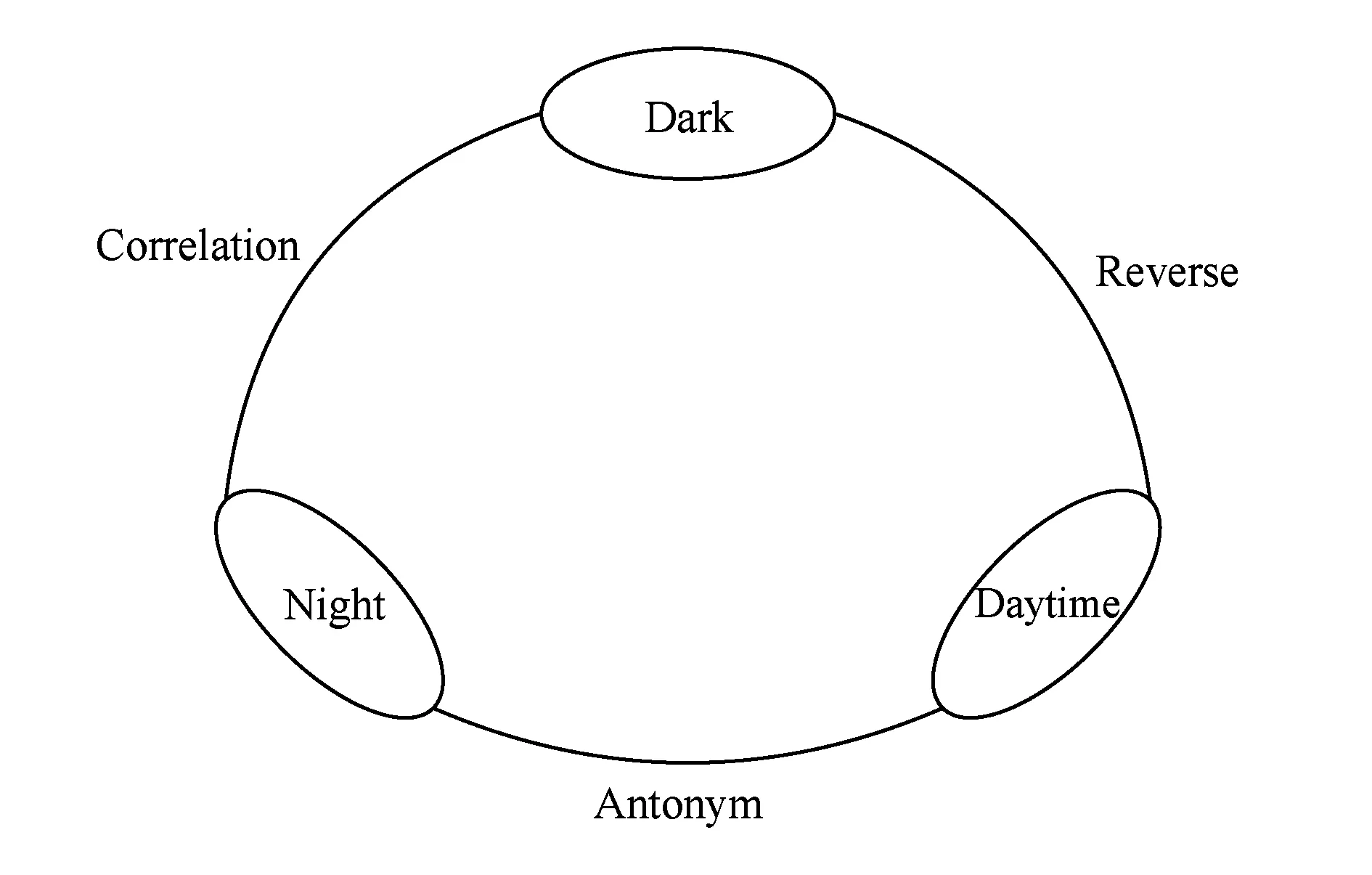
Fig. 1 Correlation application in word retention图1 相关概念应用在单词记忆中

为了研究概念之间的相关性，我们需要完成2项工作：1)选取与给定概念可能存在某种关联的概念，组成相关概念集合Vc；2)对相关概念集合按照某种算法进行相关性排序，筛选出最相关的部分概念，用于建立知识图谱.结合整个维基百科拓扑的网络概念和普遍连通性，本文将利用基于链接距离的方法，从其他概念与给定概念之间的距离进行分析，确定相关概念集合Vc.

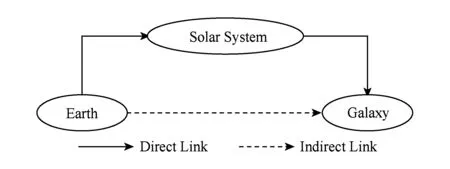
Fig. 2 Direct and indirect link in Wikipedia图2 Wikipedia中的直接和间接链接

2.3相关概念集合

维基百科中每个概念的页面中都包含了大量指向其他概念的链接，同时每个概念也被其他概念页面链接，显然这些存在直接页面链接的概念最有可能成为最相关概念，是我们分析的重点.然而维基百科的结构决定了我们并不能直接排除其他概念的相关性，因为一个页面上的超链接个数有限，显然无法将所有与给定概念相关的概念展现出来.例如“Earth”与“Galaxy”直观上是极其相关的2个概念，然而在维基百科概念拓扑图中它们直接并没有直接相连，而是通过“Solar System”间接联系，如图2所示.因此我们在建立相关概念集合时，必须将与给定概念直接或间接相连的概念(不同级别的邻接概念)都考虑在内.在通过链接距离建立相关概念集合的同时保留它们之间的距离信息(邻接度)，并以此作为计算概念之间相关性的重要参数.

假设给定概念为c，我们选取无向的维基百科概念拓扑图GU(V,E)作为研究对象，若无向图中概念a与概念b对应的顶点之间有边连接，我们称概念a与概念b邻接.定义图中与c直接邻接的概念组成的集合为c的1级邻接集合V1(c)；与V1(c)中的概念邻接，但不属于V1(c)的概念组成的集合为c的2级邻接集合V2(c)；依此类推，我们可定义出c的n级邻接集合Vn(c).n级邻接集合Vn(c)中概念v的邻接度由ac(v)表示.由以上定义和拓扑图GU的普遍连通性可知，任意不同于c的概念v，必定属于某一个邻接集合Vi(c)，且具有唯一的邻接度i.

V1(c)={v1∈V，(c,v1)∈E}， (1)

Vi+1(c)={vi+1∈V|∃vi∈Vi(c),(vi,vi+1)∈Eand ∀j≤i,vi+1∉Vj(c)}，i>1. (2)

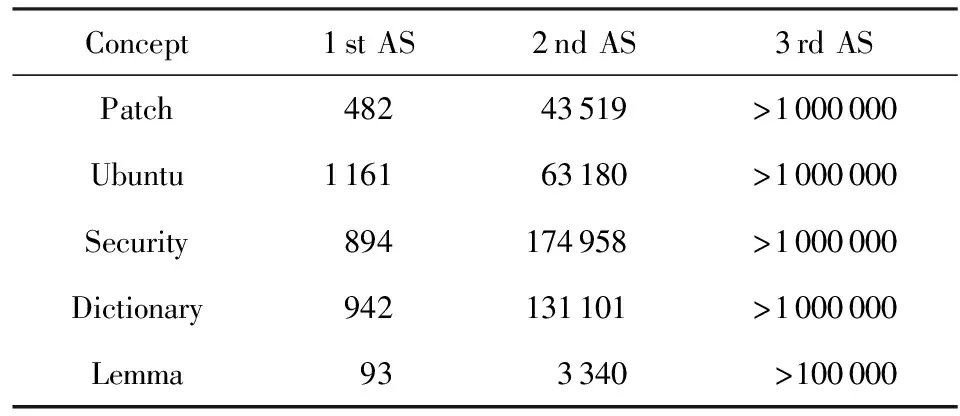
Table 2 Size of Adjacency Set (AS)表2 邻接集合规模

于是，我们需要对给定概念邻接集合的邻接度进行限制，以确定相关概念集合的大小.我们随机选取了500个概念，研究它们各级邻接集合分布情况(部分结果如表2所示).可以看出，随着邻接度的增长，邻接集合的规模增加速度极快，这是由维基百科的普遍联通性决定的，也符合概念间广泛联系的特点.大多数概念的3级邻接集合规模大于106，远远超出我们的需求；而部分概念的1级邻接集合过少，无法覆盖足够多的相关概念来建立网络.因此本文选取给定概念c的2级邻接概念集合V2(c)作为c的相关概念集合Vc，即：

Vc=V1(c)∪V2(c).

(3)

2.4基于链接的概念相关性排序算法

在通过网络拓扑获得了给定概念的邻接集合作为相关概念集合后，我们需要对相关概念集合Vc中的概念进行相关性排序.由于概念拓扑的复杂性，我们很难使用一种单独的方法既考虑到概念本身的特性又兼顾网络整体性，所以在本节中我们将采用偏重概念不同特点的排序方法，再将不同方法的排序结果进行拟合得到基于链接的概念相关性排序.

2.4.1 基于邻接概念的相似度排序

一个概念可以通过它周围近距离的概念进行一定程度上的描述，这些概念可视为给定概念的特征，且不同的概念其周围的概念一般也不同.因此我们可以仿照推荐系统中相似度判别的方法将某个概念v的1级邻接概念集合V1(v)与给定概念c的1级邻接概念集合V1(c)进行相似度判别，以此计算它们的相关性.如图3所示，白色节点为V1(c)中的元素，灰色节点为V1(v)中的元素，黑色节点为V1(v)和V1(c)的共有元素，概念v和c有一定的相关性(因为描述它们的概念有重叠部分，相关性大小可由重叠部分的占比计算).

我们引入Jaccard相似性系数Jc(v)[16]来衡量v与c的相关性：

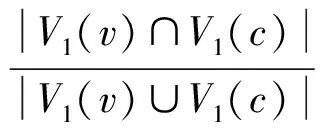
(4)

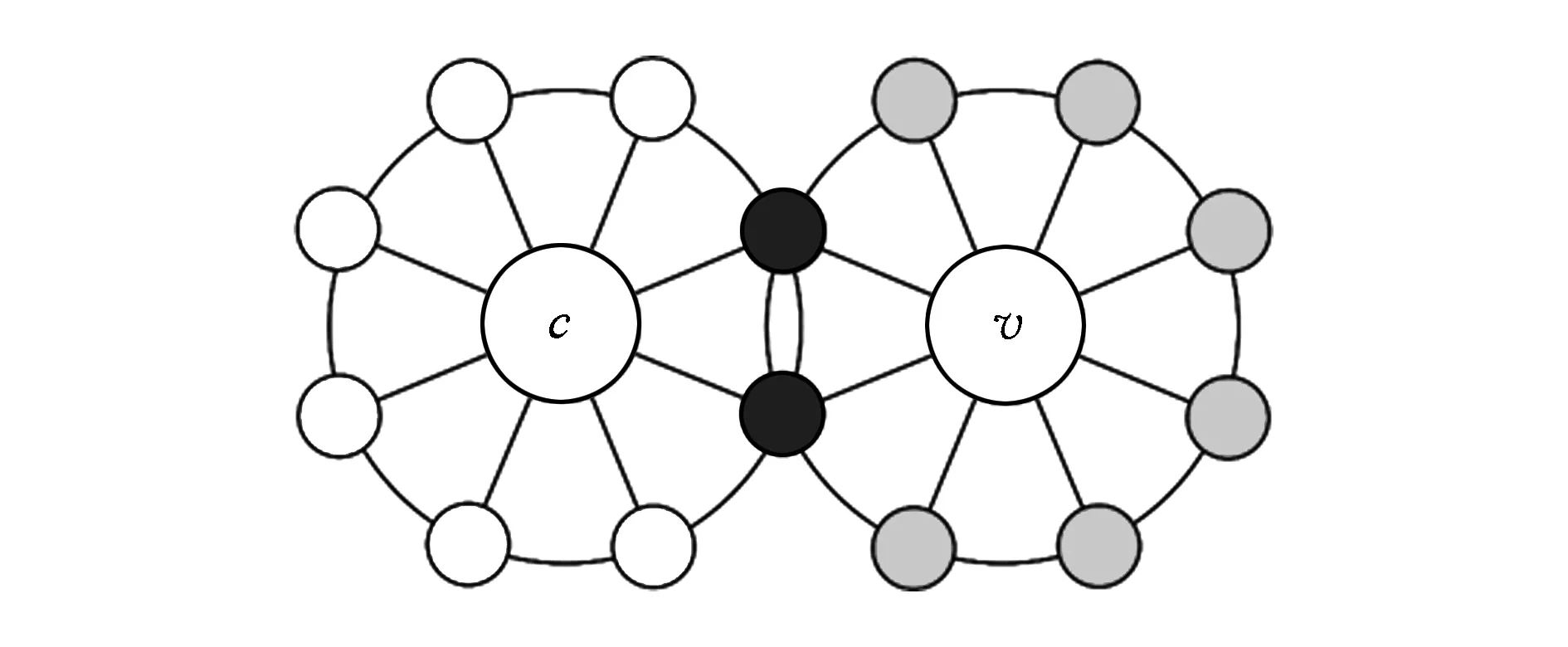
Fig. 3 Correlation calculation by overlaps of the first adjacency sets图3 1级邻接概念集的相似度计算

Jc(v)越大，即v与c的特征重合度越大，表明v和c有更强的相关性.对于给定概念c，我们在其相关概念集合Vc中对每个概念按照相关性进行排序，可得到一个最相关概念排行，如表3所示(以概念“Eigenvalues and Eigenvectors”为例).

为了验证相似度排序的准确性，我们利用另一个基于维基百科的数据集Clickstream作为测试集.该数据集以月份为单位记录了每个月中用户通过不同方式(搜索引擎、站内跳转或直接访问)访问维基百科不同概念页面的次数.截至2016年7月25日，Clickstream对英文维基百科总共提供了5个版本(201 501,201 502,201 602,201 603和201 604).为了充分利用数据集并消除热点词对访问的影响，我们将5个版本进行了组合，同时只保留站内链接跳转的数据，处理成易于访问和查询的格式，详细过程不再赘述.通过Clickstream数据集我们可以得到用户在2个概念之间双向访问的总次数，以此作为对相关概念集合Vc每个概念与给定概念相关性排行的依据，如表4所示(同样以概念“Eigenvalues and Eigenvectors”为例).

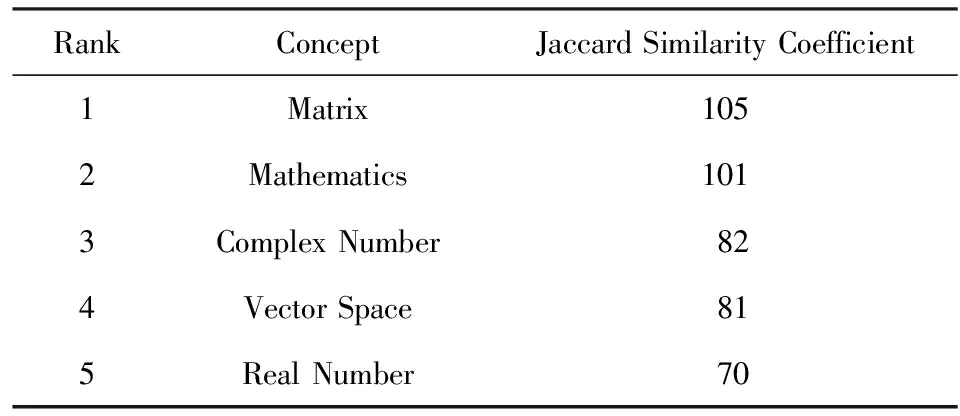
Table 3 Rank of “Eigenvalues and Eigenvectors” by JaccardSimilarity Coefficient (JSC)

Table 4 Rank of “Eigenvalues and Eigenvectors” by Clickstream表4 Clickstream中“Eigenvalues and Eigenvectors”的排序

2.4.2 基于双向链接距离的相似度排序

由表3和表4的对比我们看出，Jaccard相似性系数考虑了概念本身的特性，所以得到了较为合理的排序结果，但由于只利用了1级邻接概念集合，结果在广泛性上仍存在一些不足.为了提高排序效果，充分利用维基百科网络拓扑结构，本文提出了另一种相关性算法——标准化双向链接距离(normalized bidirectional link distance, NBLD).

Cilibrasi和Vitányi提出了基于Google判断2个单词相关性的标准化Google距离(normalized Google distance)[20]，随后Milne和Witten提出了标准化链接距离(normalized link distance, NLD)并将其应用到维基百科中[12]，NLD算法根据链入2个概念页面的链接数来计算它们的相关性.NLD算法只考虑了链入情况，然而事实上维基百科中给定概念页面中链入和链出的概念都与给定概念存在相关性.直接使用NLD算法的排序结果只覆盖了相关概念集合Vc中约17.03%的概念.于是本文提出一种标准化双向链接距离算法：

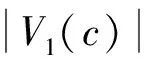
(5)

其中,W是研究对象中所有概念的集合，V1(c)和V1(v)分别是c和v的1级邻接概念集合.NBLD算法可以将相关概念覆盖率提高40%以上，以概念“Eigenvalues and Eigenvectors”为例，如表5所示:

Table 5 Rank of “Eigenvalues and Eigenvectors” by NLDand NBLD

(a) NLD

(b) NBLD

2.4.3 基于链接关系的相似度算法拟合

由表4和表5的对比可以看出，NBLD算法相比于NLD算法有更高的相关概念覆盖率，但NBLD算法过于注重概念网络整体性，忽略了概念自身的特性，结果仍不够理想.所以我们将Jaccard相似性系数和NBLD算法进行拟合，使之弥补各自的不足，获得基于链接的相似度排序算法；同时引入邻接度相关性衰减系数，使得邻接概念v与给定概念c的距离对最终结果产生加权影响.

对邻接概念集合Vc中的每个概念v与给定概念c，本文提出相关性排序算法：

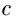
(6)

其中,γ为邻接度相关性衰减系数，取值范围为(0,1]；γ=1表示1级邻接概念和2级邻接概念权重相同，γ越趋于0表示越重视1级邻接概念的重要性.通过对整个WCT数据集的训练，我们可以确定γ的最优值.

2.5基于语义的相关性排序改进算法

2.4节提出了一种基于链接的相关性排序算法，通过维基网络拓扑的结构来自动生成指定概念c的相关概念排序.除了利用维基百科概念间的网络结构外，通过对概念之间的语义相关性进行分析也可以进一步提高概念相关性排序的准确性.

自然语言处理(natural language processing, NLP)领域的研究表明，单词可以通过神经网络计算出的分布式语义向量来表示[16].分布式语义向量表示方法，即Word Embedding，已经被应用在众多自然语言处理任务中.2个词之间的语义关联可通过计算他们的分布式语义向量间的余弦相似度来度量.而Word Embedding模型的1个重要特性是词语的相似度表示不局限于简单的句法规律,语义信息可通过语义向量的运算来获取,例如单词“King”的向量表示，通过简单的向量加减法“King”-“Man”+“Woman”，会获得1个和单词“Queen”的向量表示极为类似的向量.此外在语义向量空间中，2个具有相似上下文结构的单词其语义向量也相似.综上，利用Word Embedding可方便而准确地度量概念之间的语义关联，且这种语义关联是具有多样性的，并不局限于概念之间的语义相似.

本文提出一种基于语义的相似度算法(word embedding based, WEB)，使用Word Embedding模型来量化概念间的语义相似度，优化相关性排序结果.将Word Embedding用于知识图表示的主要挑战在于如何利用单词的语义向量表示生成概念的语义向量表示.

本文利用Word2Vec[16]计算架构的连续词袋模型(continuous bag of words model, CBOW)来训练概念的语义向量表示.CBOW模型的架构如图4所示，模型的神经网络由3层组成，包括输入层、隐藏层和输出层.基本思想是通过词w(t)的上下文内容：context{w(t-n),…,w(t-1),w(t+1),…,w(t+n)}来预测词w(t)，其中词w(t)的上下文由w(t)前后各n个词组成.上下文词的数量被称为窗口大小.模型的似然函数为

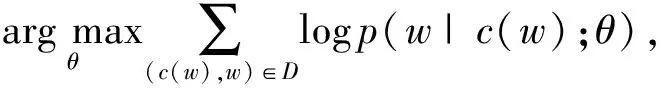
(7)

其中,w和c(w)分别代表选定词和其相关文本.(c(w)，w)是1个训练样本，D是训练样本集合.θ是待优化的参数集，包含了各词的分布式语义向量，训练算法为随机梯度上升法.需要提到的是，p(w|c(w);θ)是Softmax回归模型，在CBOW模型中有2种Softmax回归的实现方法，分层Softmax和负采样，本文中选用负采样方法.根据相关文献[16,21]，CBOW模型的上下文窗口大小设置为10，词向量的维度设置为100.

计算概念分布式语义向量

(8)

我们同样通过计算余弦相似度的方法来计算2个概念的相似度

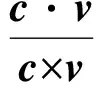
(9)

其中，c和v分别为概念c和概念v的语义向量表示.

最后，通过线性加权的方式来优化2.4节中基于链接距离的概念相似度算法

Corrc(v)=αCorrlink c(v)+(1-α)Corr_SEMc(v)，

(10)

其中，α是决定基于链接和基于语义2种相似度权重的参数.使用语义关联算法的优化效果将在实验结果及评价章节进行展示.

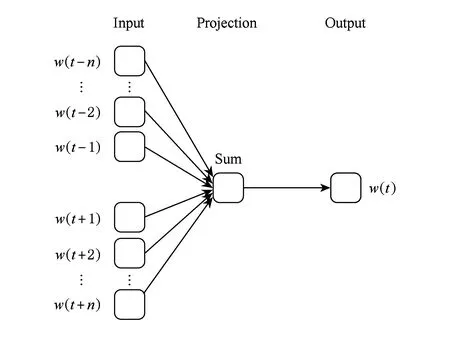
Fig. 4 The architecture of CBOW图4 连续词袋模型架构

3 实验分析

3.1评价指标

我们通过归一化折损累积增益(normalized dis-counted cumulative gain, NDCG)[22]指标，对本文提出的算法进行评估.NDCG@K被广泛应用于排序效果的评估

(11)

其中，如果某个概念排序与标准排序吻合,ri=1，否则ri=0.IDCG是人工标注的标准排序.

3.2实验设置

为了更好地评估本文提出的方法，本文进行了大量的对比实验，涉及的方法有10种：

1) JSC,单独使用JSC算法进行概念相关性排序.

2) NBLD,本文提出的标准化双向链接距离算法.

3) JSC+NBLD,本文提出的基于链接的概念相关性排序算法.

4) JSC+WEB,使用WEB算法对JSC算法进行优化.

5) NBLD+WEB,使用WEB算法对NBLD算法进行优化.

6) Finkelstein等人[13]提出的基于路径的算法.

7) Gabrilovich等人[23]提出的ESA算法.

8) Agirre等人[24]提出的基于分布式网络的相关性排序算法.

9) Milne等人[12]提出的一种基于超链接的相似度算法.

10) 本文方法,通过WEB算法对基于链接的概念相关性排序算法优化.

3.3参数设置

本文提出方法在实验中涉及的重要参数有2个，分别是基于链接的概念相关性算法中的邻接度相关性衰减系数以及WEB算法优化时的加权系数α.经过训练后，衰减系数γ=0.7(参数优化步长0.1)，加权系数α=0.78(参数优化步长0.01).

3.4实验效果评价

通过对包括本文方法在内的10种算法进行对比实验.将相关性概念的排序结果通过NDCG@10和NDCG@50进行评价，结果如表6所示：

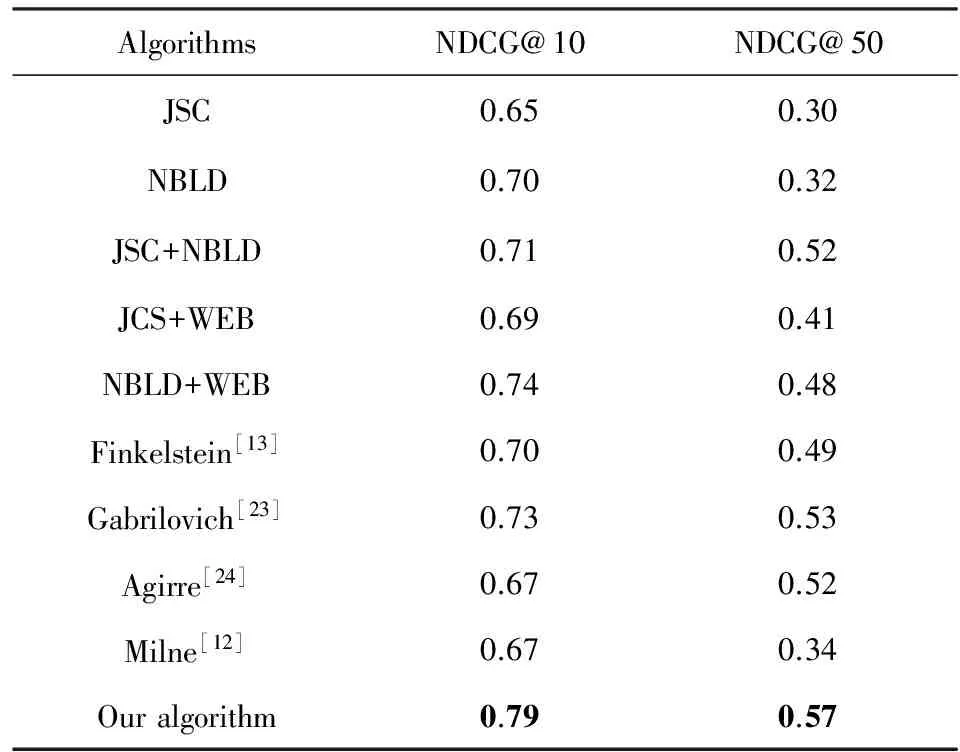
Table 6 Performance Evaluation Results of DifferentAlgorithms

实验结果显示，经过WEB算法优化后，无论是JSC算法还是NBLD算法以及基于链接的概念相关性排序算法的排序结果都有明显的提升，其中优化后的JSC算法在NDCG@50指标下排序效果提升了36.67%，JSC+NBLD方法在NDCG@10指标下提升了11.26%.可以看出，使用基于语义的概念相关性算法(WEB)明显地提升了相关概念排序的效果，这与本文的理论分析相吻合.

而本文提出的算法在与Finkelstein,Gabrilovich等人方法的比较中，获得了更好的实验结果，说明我们的方法可以更准确地描述出与给定概念最相关的概念，在概念图示化效果方面会取得更好的表现.

3.5知识图示化举例

使用本文中提出的模型，对于任何给定概念，都可以自动生成其对应的可靠的图示化表述.本节中以Neuron为例来展现这一图示化过程：

1) 选取Neuron为给定概念，找出其链入、链出的1级和2级邻接概念(1级邻接概念共1 455个，2级邻接概念共112 415个)组成相关概念集合；

2) 分别计算相关概念集合中每一个概念与Neuron的Jaccard相似性系数和标准化双向链接距离，并按照公式计算相关性，获得基于链接的相似度集合；

3) 计算Neuron与相关概念集合中其他所有概念的语义相似度，使用线性加权公式来产生最终的相似度集合.

4) 按照相关性降序排序，选出与Neuron最相关的6个概念(绘图需要)：Action potential,Axon,Brain,Neurotransmitter,Synapse,Central nervous system；

5) 分别选取这6个概念为给定概念，重复步骤1～4；

6) 将结果以图像形式展现出来，图5即为我们对概念Neuron的图示化结果.

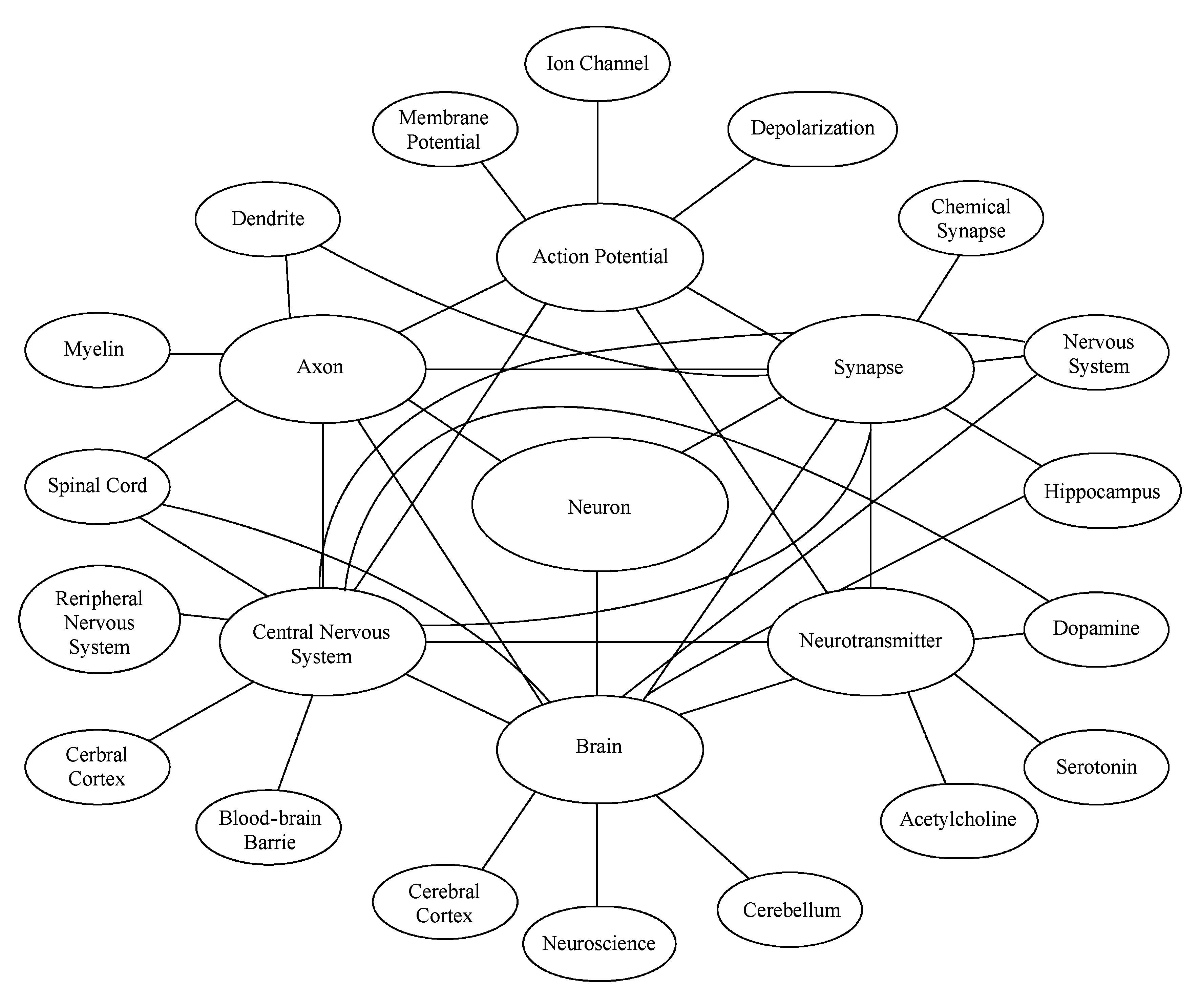
Fig. 5 Knowledge schematization of “Neuron”图5 概念“Neuron”的知识图示化

为了评估图示化结果的准确性，我们与Clickstream数据集进行对比，对于概念Neuron人类实际最关心的5个概念如表7所示，与我们生成的结果高度吻合.

Table 7 Most Correlated Concepts of Neuron by Clickstream表7 通过Clickstream对Neuron的相关概念排序

4 总 结

本文主要研究了基于维基百科的自动化图知识表示算法，利用维基百科的网络结构和概念间的语义关联，有效地建立了知识的网络拓扑结构.与前人工作不同的是，本文提出了计算机主动分析概念关系的思想，通过与记录人类点击的数据集Clickstream比较，不断完善相关性算法，使得计算机能够找出给定概念最恰当的1组相关概念，为人类学习者提供了可能的学习建议.

在研究工作初期，我们遇到数据量过大难以处理的困境，之后通过使用Hadoop集群进行分布式计算，从海量数据中抽取出研究所需的维基百科概念拓扑图，简化了后续工作的计算难度.由于我们需要对近距离概念相关性进行计算，对相关性算法的辨识度要求很高，且计算机语义分析的效果难以直接评判，于是我们使用了Clickstream数据集，依据人类点击的热度对模型进行评估.

需要指出的是，本文的工作基于维基百科进行，将维基百科的概念网络近似看作人类的知识网络.一方面来说，维基百科相较于人类知识网络更为规整和结构化，实际知识网络中2个概念之间是否有联系难以通过链接的形式简要判断，从这个角度看我们的工作有一定的理想性.但从另一个角度看，维基百科是当今人类最大的互联网百科全书，很大程度上能够代表人类的知识水平，我们通过其获得的知识结构同样具有很大的参考价值，结果不容忽视.如果我们能够获得、处理并应用更好的数据集和相关的算法，相信会取得令人更加耳目一新的成果.

[1] Brachman R J, Levesque H J, Reiter R. Knowledge Representation[M]. Cambridge: MIT Press, 1992

[2] Srinivas S, Hirtle S C. Knowledge based schematization of route directions[C] //Spatial Cognition V. Berlin: Springer, 2006: 346-364

[3] Camisón C, Forés B. Knowledge absorptive capacity: New insights for its conceptualization and measurement[J]. Journal of Business Research, 2010, 63(7): 707-715

[4] Balabanovic M, Shoham Y. Fab: Content-based, collaborative recommendation[J]. Communications of the ACM, 1997, 40(3): 66-72

[5] Sarwar B, Karypis G, Konstan J, et al. Item-based collaborative filtering recommendation algorithms[C] //Proc of the 10th Int Conf on World Wide Web. New York: ACM, 2001: 285-295

[6] Sarwar B, Karypis G, Konstan J, et al. Analysis of recommendation algorithms for e-commerce[C] //Proc of the 2nd ACM Conf on Electronic Commerce. New York: ACM, 2000: 158-167

[7] Gabrilovich E, Markovitch S. Computing semantic relatedness using Wikipedia-based explicit semantic analysis[C] //Proc of the 20th Int Joint Conf on Artificial Intelligence. San Francisco, CA: Morgan Kaufmann, 2007: 1606-1611

[8] Shirakawa M, Nakayama K, Hara T, et al. Concept vector extraction from Wikipedia category network[C] //Proc of the 3rd Int Conf on Ubiquitous Information Management and Communication. New York: ACM, 2009: 71-79

[9] Strube M, Ponzetto S P. WikiRelate! computing semantic relatedness using Wikipedia[C] //Proc of the 21st National Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2006: 1419-1424

[10] Yeh E, Ramage D, Manning C D, et al. WikiWalk: Random walks on Wikipedia for semantic relatedness[C] //Proc of the 4th Workshop on Graph-Based Methods for Natural Language Processing. New York: ACM, 2009: 41-49

[11] Dallmann A, Niebler T, Lemmerich F, et al. Extracting semantics from random walks on Wikipedia: Comparing learning and counting methods[C] //Proc of the 10th Int AAAI Conf on Web and Social Media. Menlo Park, CA: AAAI, 2016: 33-40

[12] Milne D, Witten I H. An open-source toolkit for mining Wikipedia[J]. Artificial Intelligence, 2013, 194: 222-239

[13] Finkelstein L, Gabrilovich E, Matias Y, et al. Placing search in context: The concept revisited[C] //Proc of the 10th Int Conf on World Wide Web. New York: ACM, 2001: 406-414

[14] Hoerl A E, Kennard R W. Ridge regression: Biased estimation for nonorthogonal problems[J]. Technometrics, 1970, 12(1): 55-67

[15] Singer P, Niebler T, Strohmaier M, et al. Computing semantic relatedness from human navigational paths on Wikipedia[C] //Proc of the 22nd Int Conf on World Wide Web. New York: ACM, 2013: 171-172

[16] Mikolov T, Chen K, Corrado G, et al. Efficient estimation of word representations in vector space[J]. Computer Science, 2013, abs/1301. 3781: 1-13

[17] Giles J. Internet encyclopaedias go head to head[J]. Nature, 2005, 438(7070): 900-901

[18] Gregorowicz A, Kramer M A. Mining a large-scale term-concept network from Wikipedia[J]. MITRE Corporation, 2006 [2017-02-06]. https://www.researchgate.net/publication/200773446_Mining_a_Large-Scale_Term-Concept_Network_from_Wikipedia

[19] Zhang Libo, Luo Tiejian, Sun Yihan, et al. Semantic analysis based on human thought pattern[C] //Proc of the 28th IEEE Int Conf on Bioinformatics and Biomedicine. Los Alamitos, CA: IEEE Computer Society, 2016: 1936-1939

[20] Cilibrasi R L, Vitanyi P M B. The google similarity distance[J]. IEEE Trans on Knowledge and Data Engineering, 2007, 19(3): 370-383

[21] Yazdani M, Popescu-Belis A. Computing text semantic relatedness using the contents and links of a hypertext encyclopedia: Extended abstract[J]. Artificial Intelligence, 2013, 194: 176-202

[22] Manning C D, Raghavan P, Schütze H. Introduction to information retrieval[M]. Cambridge: Cambridge University Press, 2008

[23] Gabrilovich E, Markovitch S. Wikipedia-based semantic interpretation for natural language processing[J]. Journal of Artificial Intelligence Research, 2014, 34(4): 443-498

[24] Agirre E, Alfonseca E, Hall K, et al. A study on similarity and relatedness using distributional and WordNet-based approaches[C] //Proc of Conf on the North Americ on Chapter of the ACL. Stroudsburg, PA: ACL, 2013: 19-27

KnowledgeSchematizationMethodBasedonLinkandSemanticRelationship

Yang Lin1, Zhang Libo1,2, Luo Tiejian1, Wan Qiyang1, and Wu Yanjun2

1(UniversityofChineseAcademyofSciences,Beijing101408)2(InstituteofSoftware,ChineseAcademyofSciences,Beijing100190)

How to present knowledge in a more acceptable form has been a difficult problem. In most traditional conceptualization methods, educators always summarize and describe knowledge directly. Some education experiences have demonstrated schematization, which depicts knowledge by its adjacent knowledge units, is more comprehensible to learners. In conventional knowledge representation methods, knowledge schematization must be artificially completed. In this paper, a possible approach is proposed to finish knowledge schematization automatically. We explore the relationship between the given concept and its adjacent concepts on the basis of Wikipedia concept topology (WCT) and then present an innovative algorithm to select the most related concepts. In addition, the state-of-the-art neural embedding model Word2Vec is utilized to measure the semantic correlation between concepts, aiming to further enhance the effectiveness of knowledge schematization. Experimental results show that the use of Word2Vec is able to improve the effectiveness of selecting the most correlated concepts. Moreover, our approach is able to effectively and efficiently extract knowledge structure from WCT and provide available suggestions for students and researchers.

knowledge schematization; concept topology; Word Embedding; knowledge representation; Wikipedia

born in 1989.

his bachelor’s degree in information and communication engineering from Zhejiang University, Zhejiang. Currently PhD candidate at the University of Chinese Academy of Sciences. His main research interests include recommendation system, information retrieval, machine learning and distributed storage system.

Zhang Libo, born in 1989. Received his bachelor’s degree in microelectronics from Anhui University, and received his master’s degree in electric engineering from the University of Electronic Science and Technology of China. Now assistant professor in the Institute of Software, Chinese Academy of Sciences. His main research interests include image processing, pattern recognition, knowledge graph and deep learning.

Luo Tiejian, born in 1962. PhD, professor. His main research interests include Web mining, large scale Web performance optimization and distributed storage systems.

Wan Qiyang, born in 1997. Undergraduate in the University of Chinese Academy of Sciences, Beijing. His main research interests include knowledge graph and computer education.

Wu Yanjun, born in 1979. Received his PhD degree in computer software and theory from the Institute of Software, Chinese Academy of Sciences, in 2006. Currently, professor at the Institute of Software, Chinese Academy of Sciences, Beijing. His main research interests include operating system and artificial intelligence.

2017-03-20；

：2017-05-12

中国科学院系统优化基金项目(Y42901VED2,Y42901VEB1,Y42901VEB2) This work was supported by the Foundation of Chinese Academy of Sciences for System Optimization (Y42901VED2, Y42901VEB1, Y42901VEB2).

张立波(zsmj@hotmail.com)

TP305