求解大尺度优化问题的学生t-分布估计算法
2017-08-31王豫峰董文永董学士
王豫峰 董文永 董学士 王 浩
1(武汉大学计算机学院 武汉 430072) 2(南阳理工学院软件学院 河南南阳 473000) 3 (岩土力学与工程国家重点实验室(中国科学院武汉岩土力学研究所) 武汉 430071) (wangyufeng@whu.edu.cn)
求解大尺度优化问题的学生t-分布估计算法
王豫峰1,2董文永1董学士1王 浩3
1(武汉大学计算机学院 武汉 430072)2(南阳理工学院软件学院 河南南阳 473000)3(岩土力学与工程国家重点实验室(中国科学院武汉岩土力学研究所) 武汉 430071) (wangyufeng@whu.edu.cn)
针对处理大尺度全局优化问题,提出一种基于自适应t-分布的分布估计算法(EDA-t).该算法不仅求解效果良好,而且求解速度也比同类型算法快.其基本思想是:在迭代搜索过程,首先利用期望最大化算法对演化种群进行概率主成分分析,然后根据得到的概率隐变量建立算法的概率模型,并通过t-分布自由度自适应方法,在算法收敛停滞时跳出局部最优.由于在构建模型时进行了数据降维,在不影响算法求解精度的前提下,其计算开销得到了明显降低.通过和目前主流的演化算法在大尺度优化测试函数上的仿真实验和分析,验证了所提算法的有效性和适用性.
概率主成分分析;学生t-分布;分布估计算法;大尺度全局优化;最大期望算法
分布估计算法(estimation of distribution al-gorithm, EDA)[1],是元启发算法的重要分支之一.它最开始被用于求解组合优化问题,后来扩展到求解连续优化问题.EDA是一种随机优化算法,通过对有希望的候选解采样来建立概率模型,从而探索潜在的解空间[2].通过学习的模型(单变量模型、双变量模型、多变量模型、混合变量模型),EDA可以提取变量中的一些隐藏的关系[3].例如:PBIL[4],UMDAG c[5],MIMIC[6],BMDA[7],BOA[8],IDEA[9],GMM-EDA[10]等.它们都被成功应用到很多低维优化问题中.
然而,当优化问题的维度增加时,由于问题变量之间的强相关性和高复杂度,原始的元启发算法面临着巨大的挑战.大尺度优化问题(large scale global optimization, LSGO)极难被处理,主要有2方面原因:1)维度灾难.随着问题维度的增长,搜索空间指数级地增长.2)问题维度的增长导致问题的特性(多峰、奇异点等)变得更加复杂.比如:Rosenbrock函数在两维空间中是一个单峰问题,但是,随着问题维度的增加,该函数变成多峰问题[11].当问题的维度增长时,EDA的性能下降非常快.为了克服这一个问题,一些EDA的变体算法被提出.Posik[12]提出利用独立成分分析方法对原始坐标系进行变换的遗传算法.Dong等人[13]提出一种基于模型复杂度控制的分布估计算法框架,它通过利用识别变量的弱相关行进行子空间建模.Kaban等人[14]提出一种基于随机投影的分布估计算法,它通过随机投影方式对原始协方差矩阵进行压缩.
本文提出一种基于自适应t-分布的分布估计算法(adaptive estimation of student’st-distribution algorithm, EDA-t).EDA-t利用t-分布的重尾特性在全局搜索中探索更多的解空间.在整个演化过程中,利用概率主成分分析方法学习当前最优种群的主特征隐变量空间.在学习过程中,通过期望最大值估计(expectation maximization, EM)算法代替原来的特征值分解方法,来学习当前种群主特征值的概率隐空间.根据得到的概率隐空间构建算法的概率模型,从而减少生成模型的计算开销,并加快算法收敛速度.通过对t-分布自由度的自适应,帮助算法在收敛停滞时跳出局部最优.本文提出的算法主要有3点创新:1)由传统的基于高斯分布的EDA算法扩展到学生t-分布;2)在概率模型参数的估计方面,采用EM算法来降低原始EDA估计参数的复杂度;3)由于学生t-分布的自由度参数可以控制分布的形状,自适应调整该参数能够很好地解决基于种群算法的“探索”与“开发”之间的矛盾.
1 相关工作
1.1EDA框架
EDA从提出到现在,它的变体算法使用了很多种不同的概率模型,也有很多种实现方法.但是,EDA的基本框架可以总结如算法1所示.
算法1. EDA的基本框架.
输入: 种群大小N、种群选择数K;
输出: 最优种群Popg.
①Pop0←InitialPop(N); /* 初试化种群,随机生成N个个体*/
②F0←f(Pop0); /*求出Pop0每个个体的函数值*/
③ repeat
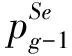
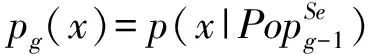
⑥Popg←getSamplePop(pg(x)); /*根据选择的个体生成概率分布*/
⑦Fg←f(Popg); /*求出Popg每个个体的函数值*/
⑧Popg←Combine(Popg-1,Popg); /*根据函数值,将种群Popg-1,Popg中的最优个体进行合并*/
⑨ until a stopping criterion is met.
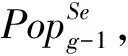
1.2学生t-分布
学生t-分布是一种统计分布.它的分布曲线呈对称钟形形状,并且曲线的图形与它的自由度υ大小有关.当υ比较小的时候,t-分布曲线中间较低,两侧尾部翘得较高;当υ增大时,分布曲线接近正态分布曲线;当υ→+∞时,t-分布曲线即为标准正态分布曲线.合理利用t-分布的这个重尾特性,能够设计出一个非常好的概率模型.
假设x是通过多元学生t-分布S(x|μ,Σ,υ)生成的D维随机变量:
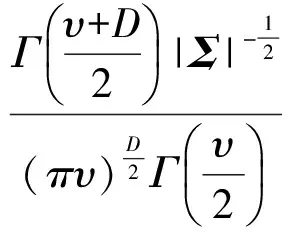
(1)
其中,μ代表均值;Σ代表正定内积矩阵;υ代表自由度,υ>0;(x-μ)TΣ-1(x-μ)代表x到μ关于Σ的马氏距离的平方;Σ-1是矩阵Σ的逆;Γ(x)代表伽马函数.当υ<2时,方差不存在.当υ>2时,Συ/υ-2就是协方差矩阵.正态分布N(μ,Σ)实际也就等于S(x|μ,Σ,∞).
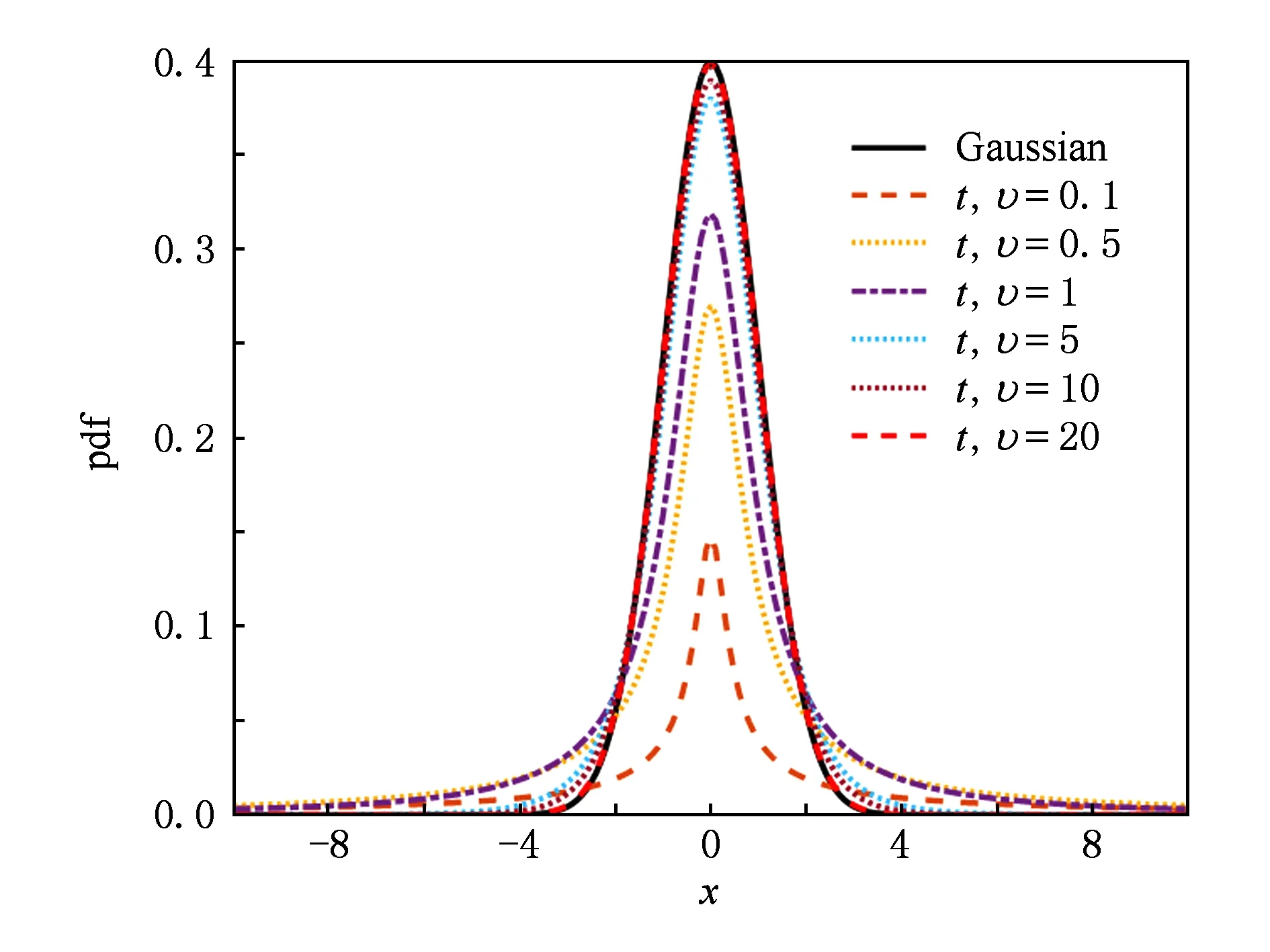
Fig. 1 Comparison between the univariate Gaussian and Students t-distributions图1 单变量t-分布和标准高斯分布对比图
为了更加清楚地理解t-分布,我们给出不同自由度下的单变量t-分布和标准高斯分布的概率密度函数图对比,如图1所示.其中,所有分布均值为0,固定方差为1.从图1中可以看到,当自由度υ比较小的时候,t-分布比高斯分布的尾部更翘.从而导致生成的个体比高斯分布有更高的概率远离均值,具有较强的全局搜索能力.在求解多峰问题的时候,更加容易逃离局部最优点,跳出停滞区.但是,它在均值点的概率密度更低,意味着减少局部搜索时间,局部微调能力降低.因此,t-分布的重尾特性有利也有弊.
2 EDA-t算法
本文提出一种新的求解大尺度优化问题的分布估计算法.算法使用基于概率隐空间建立的多元t-分布模型代替传统的高斯分布模型.通过对t-分布的自由度调整来控制算法搜索的特性.同时,引入EM算法对模型参数进行估计.和传统的PCA相比,大大减少了计算过程中的时间复杂度.
2.1概率主成分分析
传统的主成分分析需要计算数据集的均值μ和协方差矩阵Σ,然后进行特征值分解,寻找矩阵Σ的前M个最大特征值所对应的特征向量[15].而在计算特征值分解的时候,对D×D矩阵进行特征值分解的代价为O(D3).当D增大时,算法复杂度增长特别快[16].
概率主成分分析可以视为概率隐变量模型的最大似然解.其主要思想是:先根据隐变量的先验分布p(z)中生成隐变量z.然后,通过对隐变量z进行线性变换和附加噪声的方式生成观测数据点x[17].噪声服从给定隐变量下的数据变量的某个条件概率分布p(x|z).
p(z)=S(z|0,I,θ),
(2)
其中,z是一个M维隐变量,S为学生t-分布,θ为t-分布自由度,设置为固定值θ=20.
p(x|z)=S(x|Wz+μ,σ2I,υ),
(3)
W是D×M的因子载荷,μ为D维样本均值,υ为t-分布的自由度.
x=Wz+μ+ε,
(4)
ε为D维噪声变量.
p(ε)=S(ε|0,I,θ).
(5)
式(4)中有4个参数W,μ,σ2和υ,其中,υ为固定值,μ可以直接根据种群算出.W和σ2需要通过EM算法进行估计.根据概率的加和规则和乘积规则,边缘概率分布的形式为
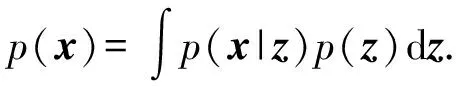
(6)
由于这对应于一个线性t-分布模型,所以,边缘概率分布还是t-分布,即:
p(x)=S(x|μ,C,υ),
(7)
其中,D×D的协方差矩阵C被定义为
C=WWT+σ2I.
(8)
在进行特征值分解计算的过程中,需要对C求逆,即需要对D×D的矩阵求逆:
C-1=σ-2I-σ-2WB-1WT,
(9)
其中,M×M的矩阵B为
B=WTW+σ2I,
(10)
由于我们对B求逆,而不是直接对C求逆.因此,计算C-1的算法复杂度从O(D3)减小到O(M3).
2.2模型参数估计方法
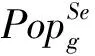
(11)
(12)
ωi∈+,1≤i≤N,是种群组合权重系数.当ωi=1/N时,式(11)就是计算所有种群的平均值.
EM是一种迭代算法.首先,通过使用旧的参数值计算隐变量的后验概率分布求期望.然后,最大化完整数据对数似然函数的期望就会产生新的参数值,直到迭代终止.完整数据的对数似然函数的形式为
lnp(X,Z|μ,W,σ2,υ)=
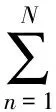
(13)
其中,矩阵Z的第n行由zn给出.均值μ由式(11)计算.分别使用式(2)和式(3)给出的隐变量概率分布和条件概率分布,对隐变量上的后验概率分布求期望,于是有:
E[lnp(X,Z|μ,W,σ2,υ)]=
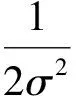
(14)
在E步,利用旧的参数去计算期望值:
(15)
(16)
在M步,估计新的参数值:
(17)
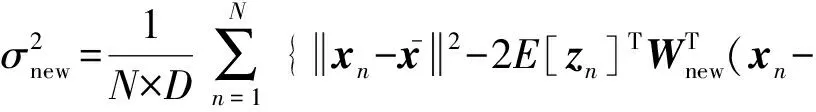
(18)
算法轮流执行E步和M步,一直到收敛.
2.3自由度自适应策略
对于t-分布,当υ=1时,t-分布就是标准柯西分布C(0,1);当υ→+∞时,t-分布趋近标准高斯分布N(0,1).柯西分布的全局探索能力较强,能够保持种群的多样性;而高斯分布的局部开发能力较强,可以保证种群的收敛精度.为了综合两者优点,通过采取自由度自适应的方法来提高算法的灵活性和求解精度.
算法在每一次迭代计算完成后,设定一个进化状态监视器U,记录当前种群中最优个体.当连续k代最优个体函数值变化为0时,出现收敛停滞状态,算法按比例α减小自由度,扩大算法全局探索能力,跳出局部最优值区域.
(19)
2.4算法框架
算法2展示了EDA-t的伪代码,算法由4个部分组成:初始化、抽样、选择和参数估计.其中,行①为初始化部分.参数W是D×M的旋转矩阵,从隐空间变化到种群原始空间,初始设置为D×D的单位矩阵前M列,参数σ初始设置为1;代码行③④为样本抽样部分;代码行⑤~⑨为样本选择部分;代码行⑩~为参数估计部分,利用新获取的种群对概率模型的参数进行估计;
算法2. EDA-t算法.
输入: 种群大小N、隐空间大小M、混合率ω、自由度υ;
输出: 最优种群Popg.
① 以随机方式初始化μ,W,σ,g=0,α=0.2,k=15;
② while 未达到终止条件时 do
③ 依据式(2)生成N个M维隐变量Z;
④ 依据式(3)生成N个D维个体X;
⑤ ifg>0 then
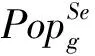
⑦ else
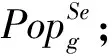
⑨ end if
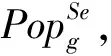
2.5算法复杂度分析
设问题维度为D,种群大小为N,隐变量大小为M.算法2中行③初始化隐变量Z的算法复杂度为O(NM);行④生成观测变量X的算法复杂度为O(ND);行⑤~⑨对种群进行重新选择组合,算法复杂度为O(N);行⑩计算种群均值算法复杂度为O(N);行通过EM算法估计参数W和参数σ.其中,EM算法的迭代次数为k,算法的复杂度为O(kNDM);在本算法中,去除所有低阶项,算法2的时间复杂度为O(kNDM).由于k、N和M都为固定值并且远远小于D,所以,整个算法的复杂度是远远小于基于特征值分解的算法O(D3).
3 仿真实验与分析
为了充分验证EDA-t算法在不同维度下的性能,实验选取了13个测试函数进行了实验分析.其中,F1-F2是可分离单峰问题;F3-F10是不可分离并且有极少(≤2)局部最优问题;F11-F13是多峰并且具有多局部最优问题.函数具体情况如表1所示,详细函数的设置见文献[13].
3.1实验设置
在对比实验中,测试问题维度为1000维,函数的最大评估次数FEs=2.5×106,实验中每一个算法对于每一个测试函数均独立运行25次.实验系统环境为64位的Windows 7系统,CPU为Intel®CoreTMi3 3.60 GHz、内存为4 GB、代码运行环境为Matlab R2015a.
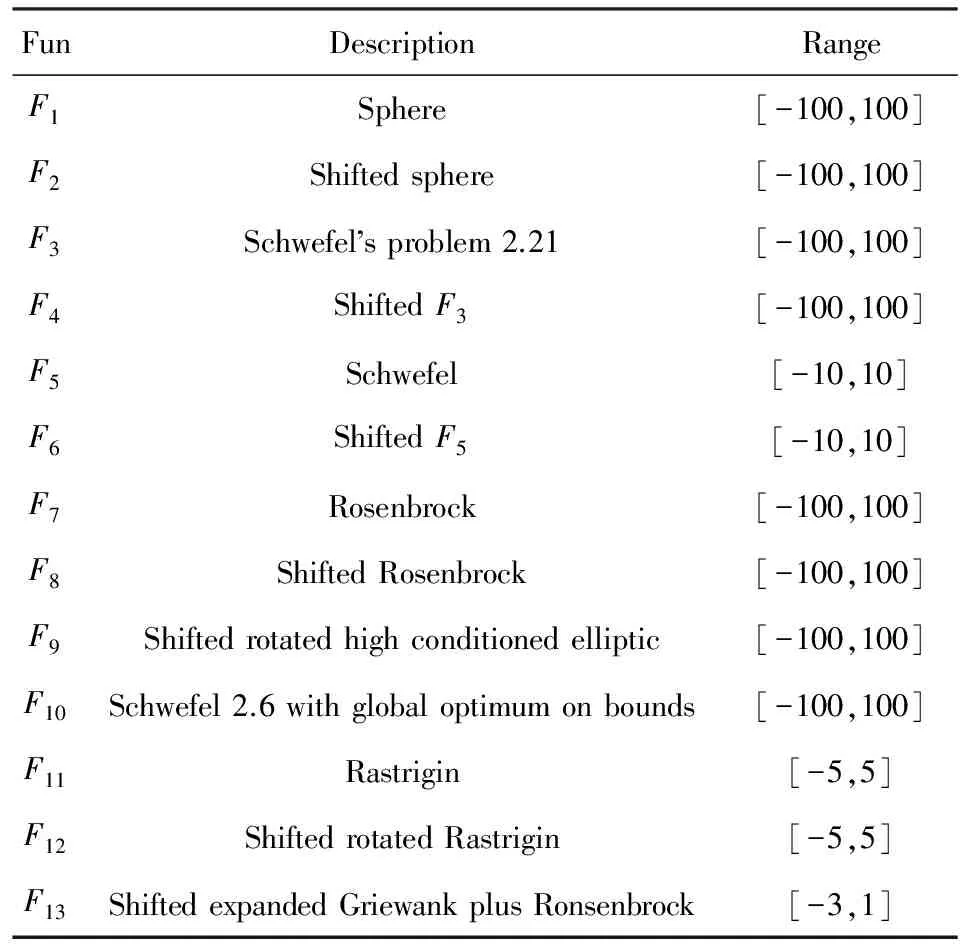
Table 1 Benchmark Functions表1 基准测试函数
在1000维实验中,选取了4个知名算法进行比较,分别是SaNSDE[18],DECC-G[19],EDA-MCC[13]和RP-EDA[14],算法参数保持与原文献一致的设置.EDA-t算法中,种群大小N=200、隐空间大小M=3、混合率ω=0.8,详细参数设置见3.4节.
为了客观公正的评价EDA-t算法的性能,采用Wilcoxon秩和检验和Friedman检验方法对实验结果进行统计分析.Wilcoxon秩和检验的显著性水平为0.05,在表2的底部的符号“-”,“+”和“≈”分别表示劣于、优于和相当于EDA-t的结果.
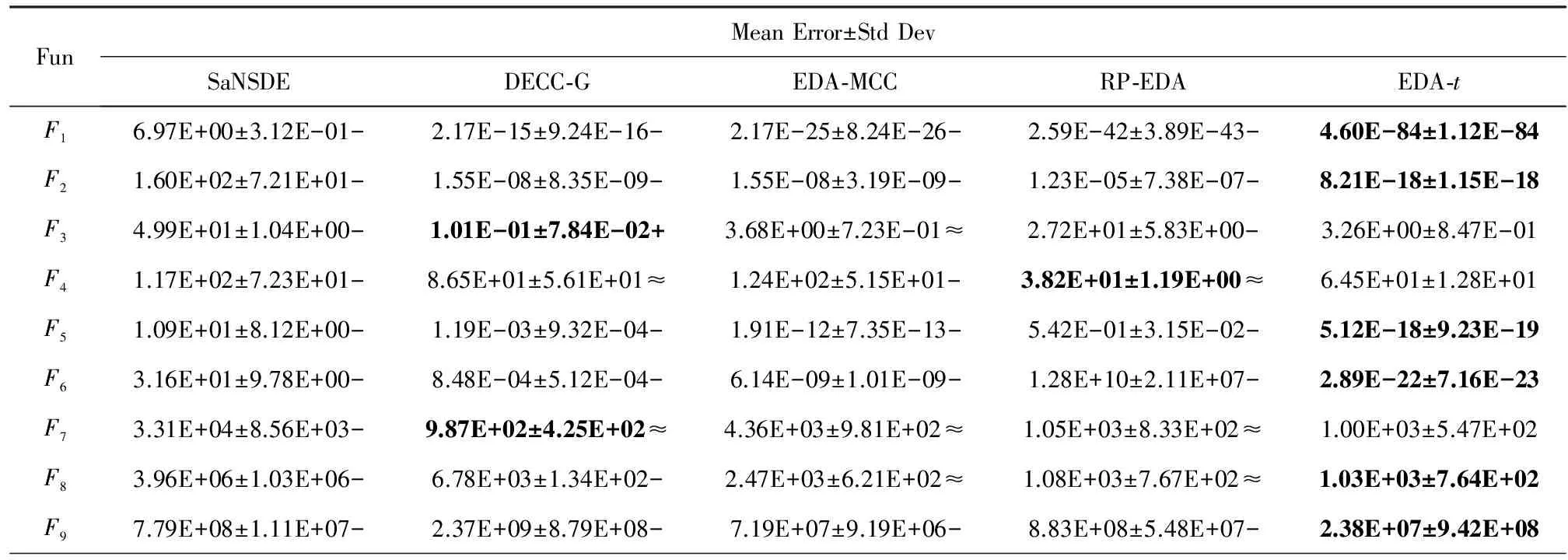
Table 2 Mean Error, Standard Deviation and Comparison Results Based on Wilcoxon’s Rank Sum Test
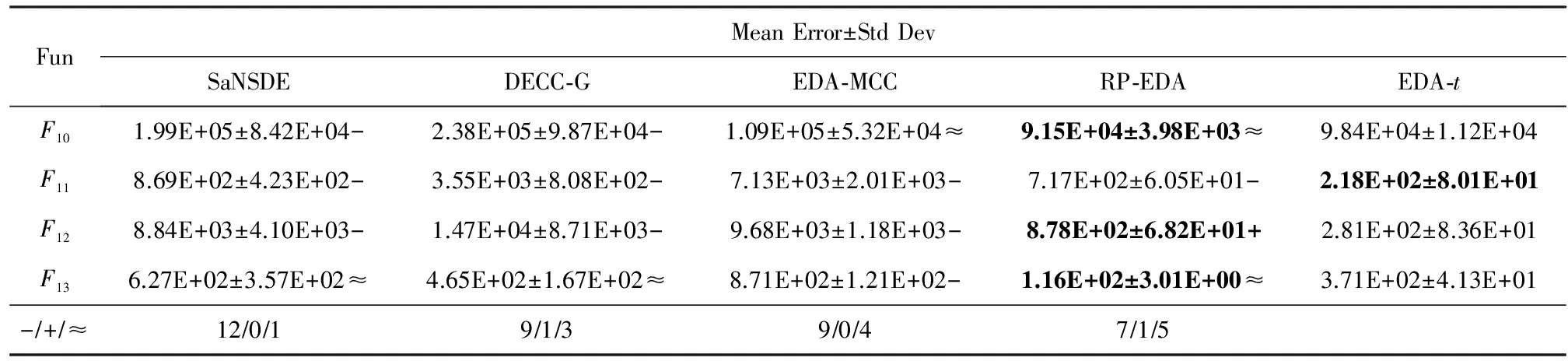
Continued (Table 2)
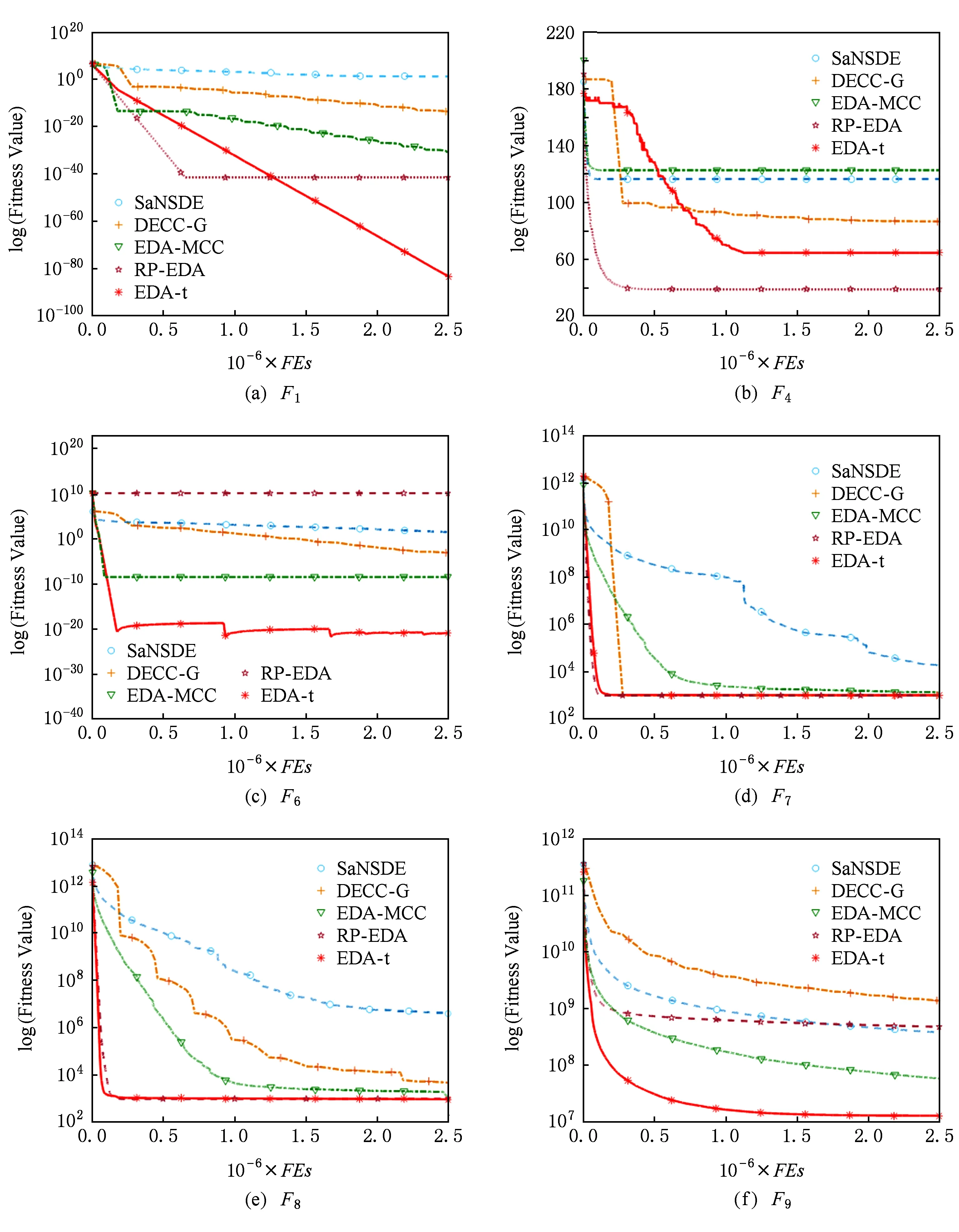
Fig. 2 Convergence curve of five algorithms on functions F1,F4,F6,F7,F8 and F9图2 各算法在函数F1,F4,F6,F7,F8和F9上的收敛曲线
3.2实验结果分析
通过表2、表3、图2和图3分析可发现,EDA-t算法在收敛速度、收敛精度和运行时间方面,与其他算法相比占有较大优势.特别是在F1,F2,F5,F6,F8和F9测试函数上,EDA-t算法可以快速收敛,并取得最优解.
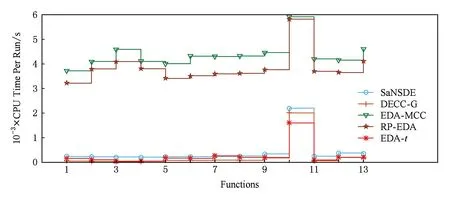
Fig. 3 CPU time per run of five algorithms图3 各算法的运行时间
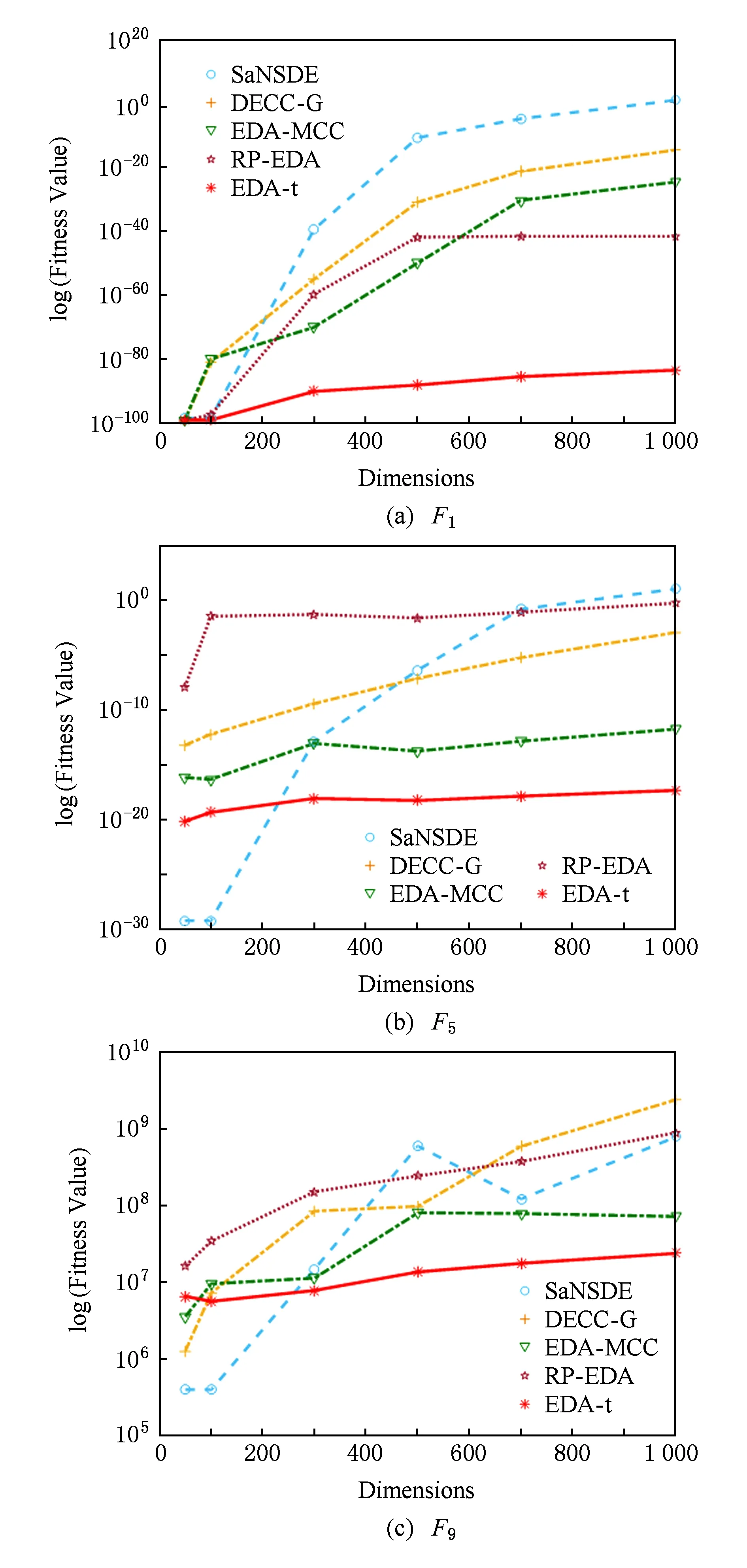
Fig. 4 Fitness value of five algorithms on different dimensions图4 各个算法在不同维度下收敛精度
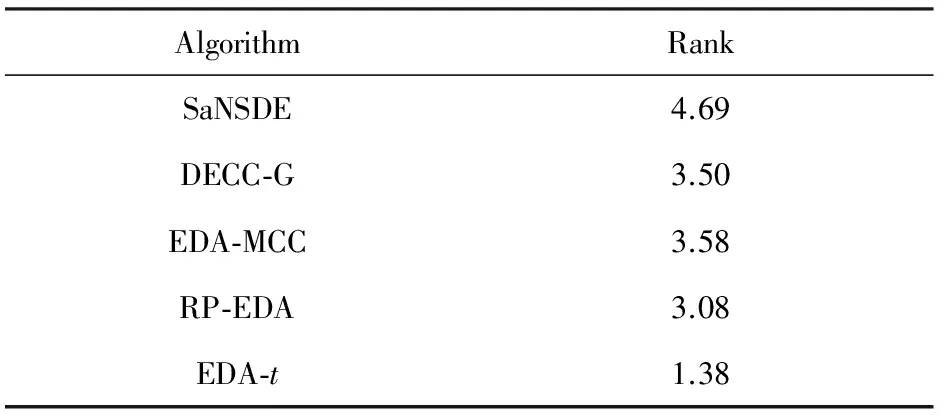
AlgorithmRankSaNSDE4.69DECC⁃G3.50EDA⁃MCC3.58RP⁃EDA3.08EDA⁃t1.38
在表2中,EDA-t除F3,F7和F13三个函数外均全面优于SaNSDE和DECC-G.SaNSDE采用邻域搜索的差分演化算法,该算法对低维的优化问题能取得较好的解.但是,对高维优化问题的搜索代价过大,往往不能得到很好的解.DECC-G是采用随机分组的协同演化算法,对于大尺度可分离优化问题能够得到较好的解.但是,对于非可分的优化问题,求解效果不太好.因此,EDA-t在求解大尺度全局优化问题全面优于这2种算法.
EDA-t在F1,F2,F5,F6,F9,F11和F12七个函数上要优于EDA-MCC和RP-EDA,在F3,F4,F7,F8,F10和F13六个函数上表现相似.EDA-MCC通过识别变量之间的弱相关性来控制模型的复杂度,而变量之间的相关性识别准确率直接影响算法的求解精度.RP-EDA通过将个体随机投影到低维空间,然后在低维空间抽样再还原到原始空间的方式进行演化,在演化的过程中具有很大的随意性.EDA-t是通过隐空间建立概率模型,在全局搜索的过程按当前种群主成分方向进行引导搜索,进而搜索更有效率,带来更优解.
从表2底部的Wilcoxon秩和检验的统计结果可以看出,EDA-t算法相对于其他近几年出现的国际知名算法更具有明显的优势.表3给出了EDA-t和其他算法的Friedman检验排名,EDA-t排在第一,从统计学上说明了DECC-CLV算法的优势.从图3可以看出,EDA-t算法和其他EDA优化算法(EDA-MCC和RP-EDA)相比,算法单次运行时间大大降低.并且,基于非分解策略的EDA-t算法运行时间已经比较接近基于分解策略的协同演化算法DECC-G.
综合以上实验分析可以说明EDA-t算法具有较快的收敛速度、较强的收敛精度和较好的函数适用性,有效提高了对大尺度全局优化问题的收敛效率.
3.3算法的稳定性分析
为了测试算法在不同维度下的表现稳定性情况,我们将所有对比算法分别在不同问题维度D=[50,100,300,500,700,1 000]情况下,进行对比实验.由于篇幅有限,我们从大尺度的测试函数中选F1,F5和F9三个函数进行测试.
从图4可以看出,对于大尺度全局优化问题,当问题维度小于300时,EDA-t劣于SaNSDE.因为SaNSDE是基于领域搜索的差分演化算法,在对待低维问题,可以充分发挥SaNSDE全局的搜索能力,求到最优解.但是,当问题维度增加时,基于领域搜索的策略导致SaNSDE算法搜索开销增大,性能降低.当问题维度大于300的时候,EDA-t算法在不同维度下都要比其他各种算法表现要好,表现出了算法的稳定性.
3.4参数敏感性实验
为了研究算法中参数的不同设置对于算法性能的影响.在本节中,首先对种群大小N的不同取值进行对比实验.然后,在种群大小固定的前提下,通过使用不同的参数设置进行对比实验.在本节对比实验中,函数的最大评估次数FEs=1 000×D.
从表4可以看出,在不同的问题维度下,EDA-t取得最优值时,所需的种群大小也不一样.因为,本文算法是在1000维下和其他知名算法进行对比实验.所以,在实际计算中,种群大小设置为N=200.
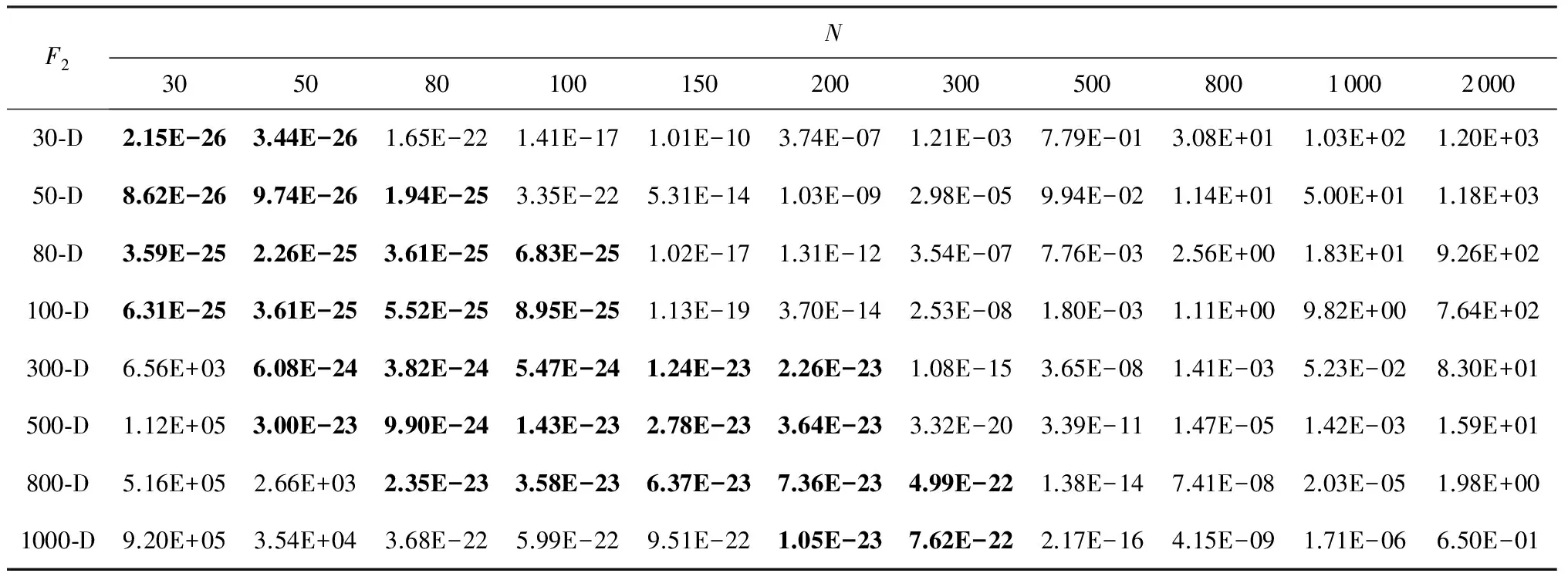
Table 4 Experimental Results of Different N on F2表4 F2函数上不同种群大小N的对比实验
我们对参数M,ω,υ进行正交对比实验,隐空间大小M=[1,3,5,7];混合率ω=[0.8,0.6,0.4];自由度υ=[5,20,100,200].由于篇幅限制,文中只列出F5、F7和F11函数的实验结果图.
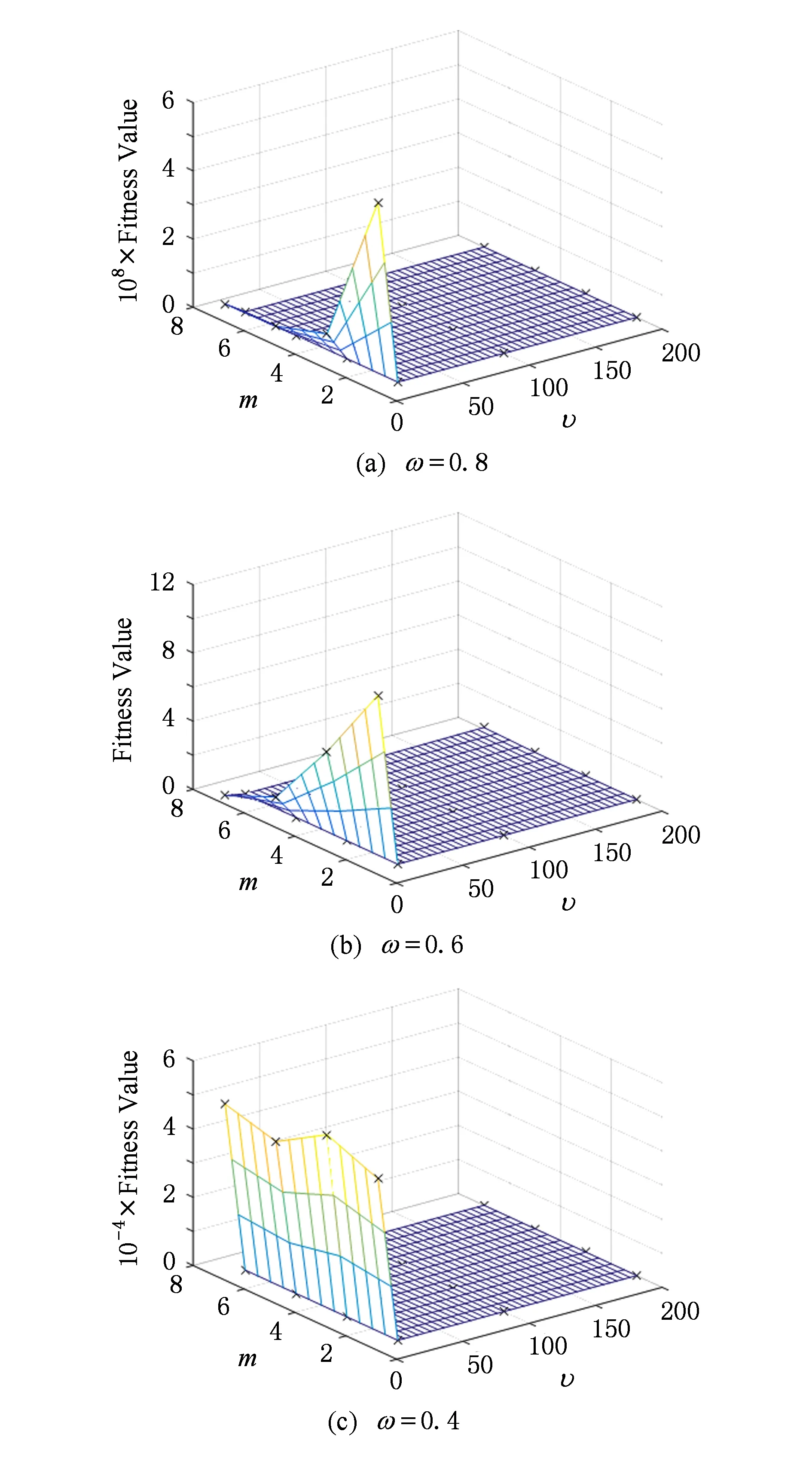
Fig. 5 Mesh grid of different parameters on functions F5图5 不同参数在函数F5上的曲面网状图
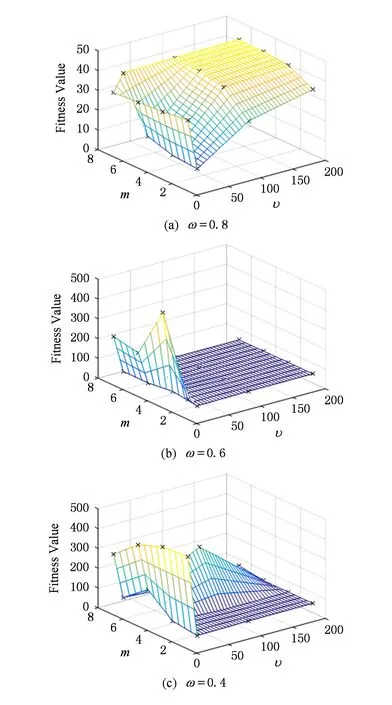
Fig. 6 Mesh grid of different parameters on functions F7图6 不同参数在函数F7上的曲面网状图
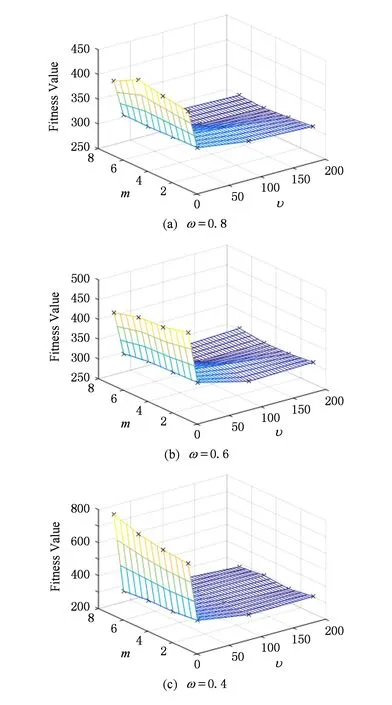
Fig. 7 Mesh grid of different parameters on functions F11图7 不同参数在函数F11上的曲面网状图
从图5~7可以看出,当M≥3时,算法的求解精度逐渐变好.但是,随着M的变大,算法的复杂度也加倍变大.所以,当M=3时,可以较好地平衡求解精度和算法复杂度.当ω=0.8时,EDA-t算法采用不同参数设置所取得的最差求解精度,也要比ω=0.4和ω=0.6所得到的求解精度好,表现了较强的鲁棒性.算法自由度υ从5变为20时,算法的求解精度明显变好.但是,当υ继续增大时,算法求解精度的变化不是很大.综上分析,在综合考虑算法计算代价与计算精度的平衡,算法参数可以取M≥3,ω=0.8和υ=20.
3.5自由度自适应策略有效性分析
为了研究t-分布的自由度自适应策略对算法性能的影响,在本节中,使用自由度固定的EDA-t算法和自由度自适应的EDA-t算法进行对比实验.EDA-t中的固定自由度按3.4节中最优值进行设置,υ=20.对比实验结果如表5所示.
从表5可以看出,EDA-t算法全面优于EDA-t算法,表明采取自由度自适应策略在整个演化过程中可以有效避免陷入局部最优.从而快速收敛到局部最优,并表现出较好的稳定性.
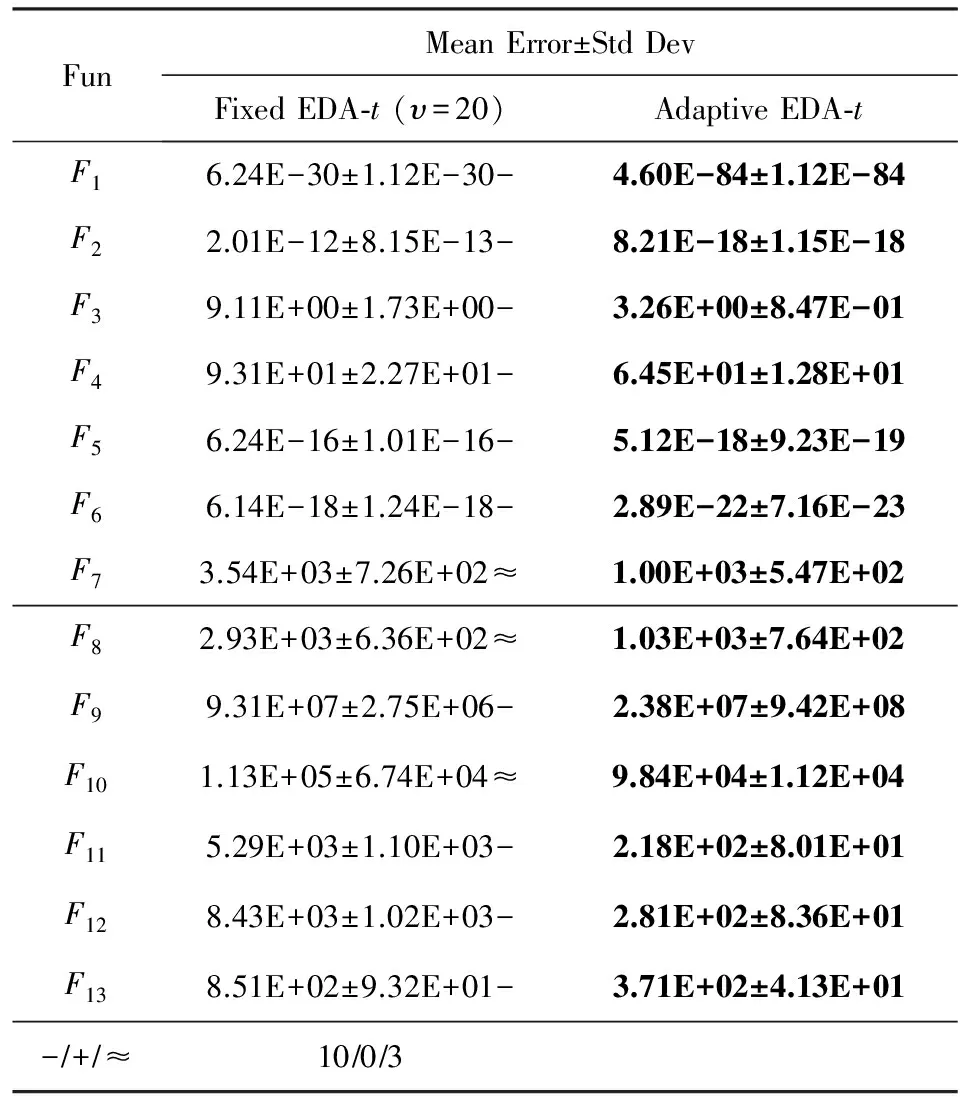
Table 5 Experimental Results of Fixed EDA-t andAdaptive EDA-t
3.6概率PCA的有效性分析
为了研究ED-t中使用概率PCA对算法性能的影响,在本节中,使用基于PCA的EDA-t算法和基于概率PCA的EDA-t算法进行对比实验.对比实验结果如表6、表7所示.
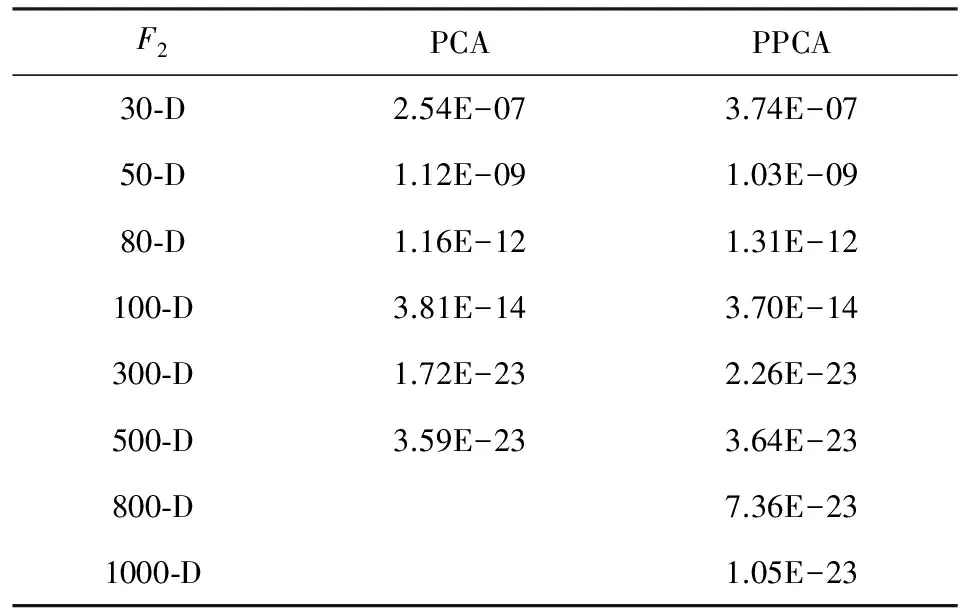
Table 6 Experimental Results of EDA-t Based on PCAand PPCA
从表6、表7中可以看出,当EDA-t使用PCA而不使用概率PCA的时候,算法求解精度变化不太大.但是,算法求解的时间随着问题维度的增加而急剧增加,直接导致算法在问题维度大于500维的时候,因为运算超时而无法求解.
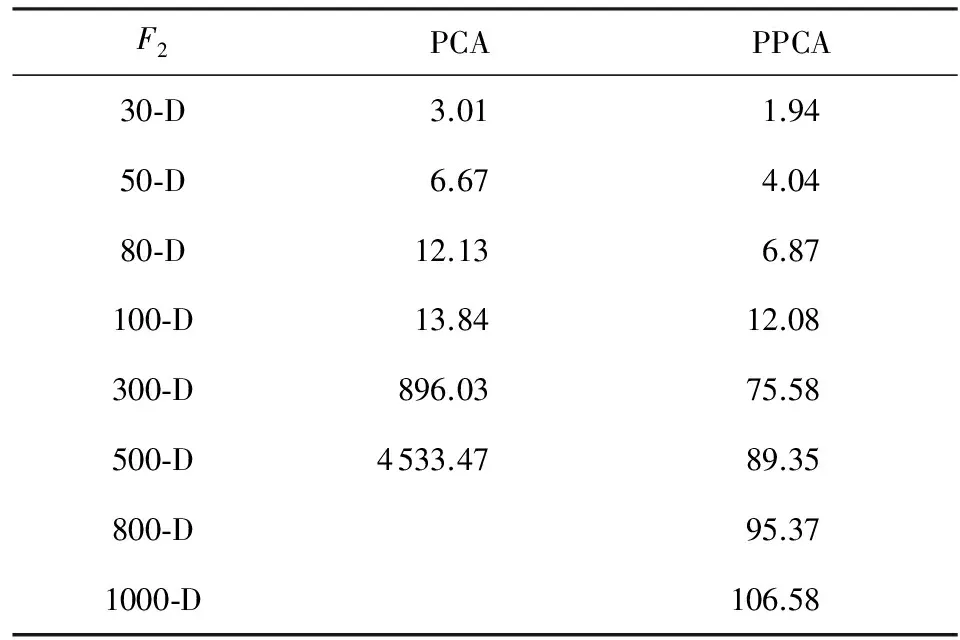
Table 7 CPU Time of EDA-t Based on PCA and PPCA
4 总 结
本文提出了一种新的基于自适应t-分布的分布估计算法EDA-t.它通过对t-分布自由度自适应的调节,提高了算法的全局探索能力和跳出局部最优停滞区的能力.通过使用隐空间的转换,加快了算法的收敛速度.通过对13个大尺度全局优化进行测试,实验结果表明与当前主流算法相比,本文算法在求解的精度与收敛速度上具有更优的性能.另外,如何将算法与实际问题相结合是未来研究工作的重点.
[1] Muhlenbein H, Bendisch J, Voigt H M. From recombination of genes to the estimation of distributions Ⅱ. Continuous parameters[C] //Proc of the Int Conf on Parallel Problem Solving From Nature Ⅳ. Berlin: Springer, 1996: 188-197
[2] Hauschild M, Pelkan M. An introduction and survey of estimation of distribution algorithms[J]. Swarm & Evolutionary Computation, 2011, 1(3): 111-128
[3] Zhang Bo, Hao Jie, Ma Gang, et al. Mixture of probabilistic canonical correlation analysis[J]. Journal of Computer Research and Development, 2015, 52(7): 1463-1476 (in Chinese)(张博, 郝杰, 马刚, 等. 混合概率典型相关性分析[J]. 计算机研究与发展, 2015, 52(7): 1463-1476)
[4] Sebag M, Ducoulombier A. Extending population-based incremental learning to continuous search spaces[C] //Proc of the Parallel Problem Solving From Nature Ⅴ. Berlin: Springer, 1998: 418-427
[5] Larraaga P, Lozano J A. Estimation of distribution algorithms. A new tool for evolutionary computation[J]. IEEE Trans on Instrumentation & Measurement, 2002, 64(5): 1140-1148
[6] Bonet J S D, JR C L I, Viola P A. MIMIC: Finding optima by estimating probability densities[C] //Advances in Neural Information Processing Systems. Cambridge: MIT Press, 1997: 424-430
[7] Pelikan M, Muehlenbein H. The bivariate marginal distribution algorithm[M]. Berlin: Springer, 1998: 521-535
[8] Pelikan M, Goldberg D E, Cant E. BOA: The Bayesian optimization algorithm[C] //Proc of the 1st Conf on Genetic and Evolutionary Computation. San Francisco: Morgan Kaufmann, 1999: 525-532
[9] Bosman P A N, Thierens D. Expanding from discrete to continuous estimation of distribution algorithms: The IDEA[C] //Proc of the Int Conf on Parallel Problem Solving From Nature Ⅵ. Berlin: Springer, 2000: 767-776
[10] Lu Qiang, Yao Xin. Clustering and learning gaussian distribution for continuous optimization[J]. IEEE Trans on Systems Man & Cybernetics Part C Applications & Reviews, 2005, 35(2): 195-204
[11] Shang Yunwei, Qiu Yuhuang. A note on the extended Rosenbrock function[J]. Evolutionary Computation, 2006, 14(1): 119-126
[12] Posik P. On the utility of linear transformations for population-based optimization algorithms[C] //Proc of the 16th Congress of the Int Federation of Automatic Control. Prague: IFAC, 2005: 281-286
[13] Dong Weishan, Chen Tianshi, TINO P, et al. Scaling up estimation of distribution algorithms for continuous optimization[J]. IEEE Trans on Evolutionary Computation, 2013, 17(6): 797-822
[14] Kab N A, Bootkrajang J, Durrant R J. Toward large-scale continuous EDA: A random matrix theory perspective[J]. Evolutionary Computation, 2016, 24(2): 255-291
[15] Fang Minquan, Zhang Weimin, Zhou Haifang. Parallel algorithm of fast independent component analysis for dimensionality reduction on many integrated core[J]. Journal of Computer Research and Development, 2016, 53(5): 1136-1146 (in Chinese)(方民权, 张卫民, 周海芳. 集成众核上快速独立成分分析降维并行算法[J]. 计算机研究与发展, 2016, 53(5): 1136-1146)
[16] Zhang Cheng, Wang Dong, Shen Chuan, et al. Separable compressive imaging method based on singular value decomposition[J]. Journal of Computer Research and Development, 2016, 53(12): 2816-2823 (in Chinese)(张成, 汪东, 沈川, 等. 基于奇异值分解的可分离压缩成像方法[J]. 计算机研究与发展, 2016, 53(12): 2816-2823)
[17] Bishop C M. Pattern recognition and machine learning[M]. Berlin: Springer, 2006, 571-586
[18] Yang Zhenyu, Tang Ke, Yao Xin. Self-adaptive differential evolution with neighborhood search[C] //Proc of IEEE World Congress on Computational Intelligence, NJ: IEEE, 2008: 1110-1116
[19] Yang Zhenyu, Tang Ke, Yao Xin. Large scale evolutionary optimization using cooperative coevolution[J]. Information Sciences, 2008, 178(15): 2985-2999
AdaptiveEstimationofStudent’st-DistributionAlgorithmforLarge-ScaleGlobalOptimization
Wang Yufeng1,2, Dong Wenyong1, Dong Xueshi1, and Wang Hao3
1(ComputerSchool,WuhanUniversity,Wuhan430072)2(SoftwareSchool,NanyangInstituteofTechnology,Nanyang,Henan473000)3(StateKeyLaboratoryofGeomechanicsandGeotechnicalEngineering(InstituteofRockandSoilMechanics,ChineseAcademyofSciences),Wuhan430071)
In this paper, an adaptive estimation of student’st-distribution algorithm (EDA-t) is proposed to deal with the large-scale global optimization problems. The proposed algorithm can not only obtain optimal solution with high precision, but also run faster than EDA and their variants. In order to reduce the number of the parameters in student’st-distribution, we adapt its closed-form in latent space to replace it, and use the expectation maximization algorithm to estimate its parameters. To escape from local optimum, a new strategy adaptively tune the degree of freedom in thet-distribution is also proposed. As we introduce the technology of latent variable, the computational cost in EDA-tsignificantly decreases while the quality of solution can be guaranteed. The experimental results show that the performance of EDA-tis super than or equal to the state-of-the-art evolutionary algorithms for solving the large scale optimization problems.
probabilistic PCA; student’st-distribution; estimation of distribution algorithm (EDA); large scale global optimization (LSGO); expectation maximization (EM) algorithm

Wang Yufeng, born in 1982. PhD candidate of Wuhan University. Student member of CCF. His main research interests include machine learning, evolutionary computation, data dimension reduction.

Dong Wenyong, born in 1973. Professor and PhD supervisor in Wuhan University. His main research interests include evolutionary computation, system control, machine learning, parallel computing.

Dong Xueshi, born in 1985. PhD candidate of Wuhan University. His main research interests include evolutionary computation, machine learning.

Wang Hao, born in 1972. PhD. Research Professor in the Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan. His main research interests include evolutionary computation, machine learning.
2017-03-17;
:2017-05-15
国家自然科学基金项目(61170305,61672024,41472288);河南省高等学校重点科研项目计划(17A520046) This work was supported by the National Natural Science Foundation of China (61170305,61672024,41472288) and the Key Research Program in Higher Education of Henan Province (17A520046).
董文永(dwy@whu.edu.cn)
TP301
