基于事故树的隧道塌方风险评估

南宇宏,赵 颂,羊正茂

(中铁科学研究院有限公司,四川成都 611731)

基于事故树的隧道塌方风险评估

南宇宏,赵 颂,羊正茂

(中铁科学研究院有限公司,四川成都 611731)

基于隧道施工中常见安全事故原因的调查和分析,对隧道施工阶段常见风险因素和危险环境进行辨识,并采用事故树分析方法,建立隧道塌方事故树模型,对隧道施工塌方顶事件进行了定性和定量分析。最终得出隧道塌方26个基本事件的结构重要度序列以及隧道塌方事件概率重要度和临界重要度分析方法;通过工程实例分析发现,采取措施前后塌方的发生概率从0.006 225降至0.000 941。

隧道工程;塌方分析;事故树分析;概率模型

0 引 言

近年来,中国基础设施建设迅速发展,海底隧道、山岭隧道和地下隧道等的建设进入高潮,隧道工程灾害也日益得到业内的关注,其中塌方是最严重的灾害之一[1-4]。目前,国内外关于隧道的研究主要集中在设计及施工技术方面[5-9],塌方风险评估只取得了一些理论成果[10-13]。本文主要从实用技术的角度出发,采用演绎推理的方法,用事故树模型演绎隧道塌方的直接或间接原因,为隧道塌方事后分析或预防提供决策依据。

1 隧道塌方影响因素辨识

1.1 隧道塌方因素统计分析

1.1.1 地质状况

复杂的地质状况具有多变性和不可预见性,主要与围岩级别、地下水、结构面产状、特殊地质有关。其中围岩级别决定隧道选址及支护类型,围岩级别越高,稳定性越差,塌方的风险就越大。断层面、层理、不整合接触面、节理及软弱夹层等结构面都可使岩体成为一种不连续介质,导致塌方事件的发生。另外,隧道施工过程中遇到的膨胀性围岩、溶洞、高应力、湿陷性黄土等特殊地质段,也极易使围岩不稳定而导致塌方。

1.1.2 施工工艺

勘察工作深度、隧道埋深、开挖跨度及支护强度等都与隧道塌方息息相关。其中,随着开挖跨度增大,隧道塌方比例呈上升趋势。尽管线路设计要求避开特殊地质结构,但当有些特殊地层由于勘察不到位或者无法绕行时,设计的支护体系不足以维持围岩的稳定性,或者选择的开挖方法不合理,都会导致塌方事故的发生。

围岩原始的平衡被打破是隧道塌方的起因,也是必要条件。在施工过程中,影响围岩应力重分布的主要因素有断面大小、钻爆控制、开挖机械扰动、开挖工法、循环进尺、工序安排。

1.1.3 施工质量

隧道施工主要采用爆破、人工或机械开挖等方法,支护以人工操作为主。当隧道原有的应力平衡被打破,必然要进行应力重分布;为限制应变,一般在开挖前采取超前预支护等辅助措施,开挖后采取支护措施,以预防塌方事件的发生。但是,实际施工中超前预支护往往得不到重视,常见的有预处理加固不到位、超前支护不符合要求、排水措施不到位、监控量测反馈不及时,这些都会给隧道施工埋下安全隐患。

1.1.4 安全管理

安全管理是隧道施工阶段管理的重要部分,安全管理工作不到位既影响施工过程控制,也危及施工人员的安全[14-16]。由于管理因素属于软科学范畴,目前不能直接与其他现场风险因素拟合,为此本文在事故树分析中将其在安全管理评估表中单独评价。

在研究隧道工程塌方风险中,考虑到隧道设计的特征属于动态化设计,假定隧道设计都能保证施工安全,建立隧道塌方风险因素辨识结果,如图1所示。

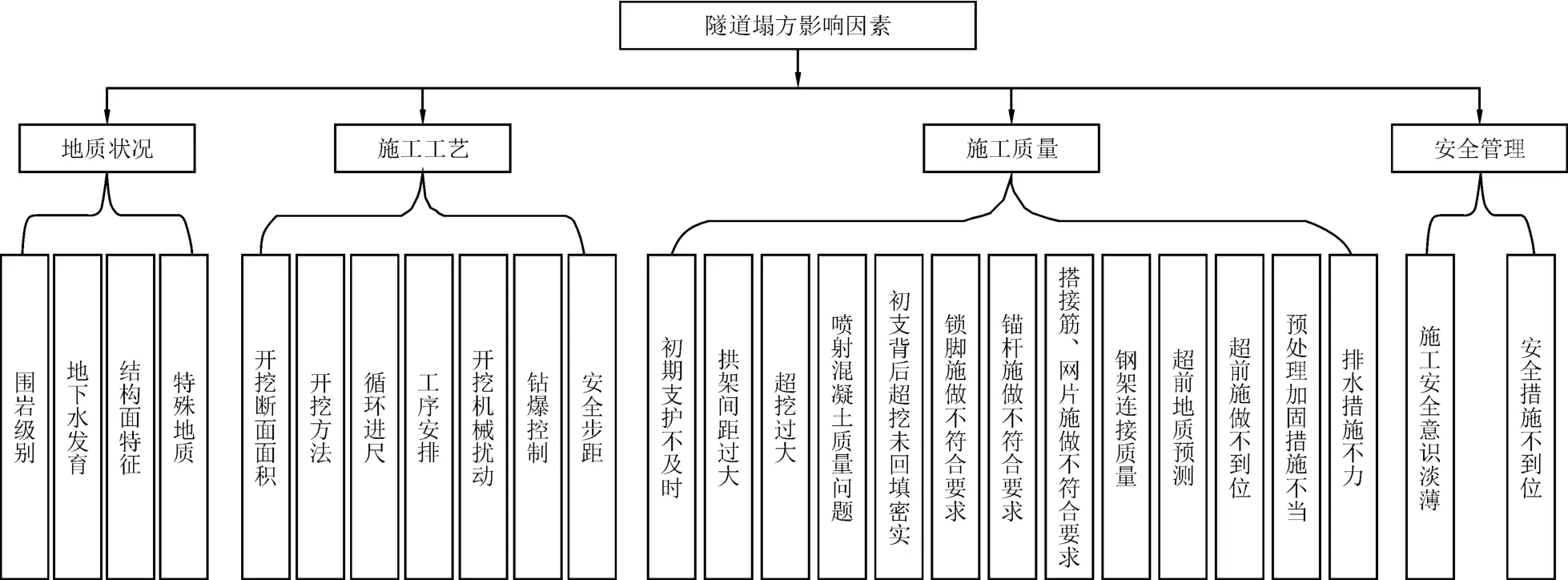
图1 隧道塌方影响因素辨识结果

2 事故树分析

2.1 事故树模型的建立

根据图1和资料统计结果,确定隧道塌方事故树事件及其对应的符号,如表2所示。根据各事件之间的逻辑关系,建立事故树模型(图2)。其中,符号T表示顶事件(隧道塌方)。事故树的定性、定量分析通过最小割集或最小径集实现。

2.2 最小割集

为了便于数学计算,将图2所示事故树等效描述为布尔代数表达式的形式

其中

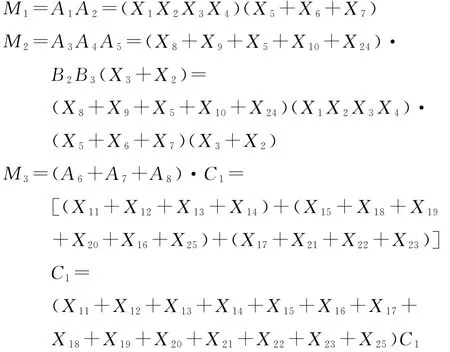
对式(1)进行化简,得到隧道塌方事故树结构函数表达式

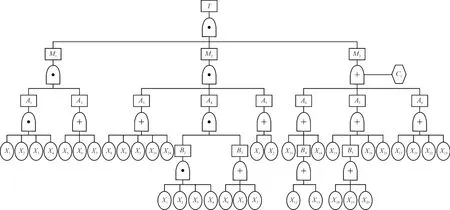
图2 隧道塌方事故树模型

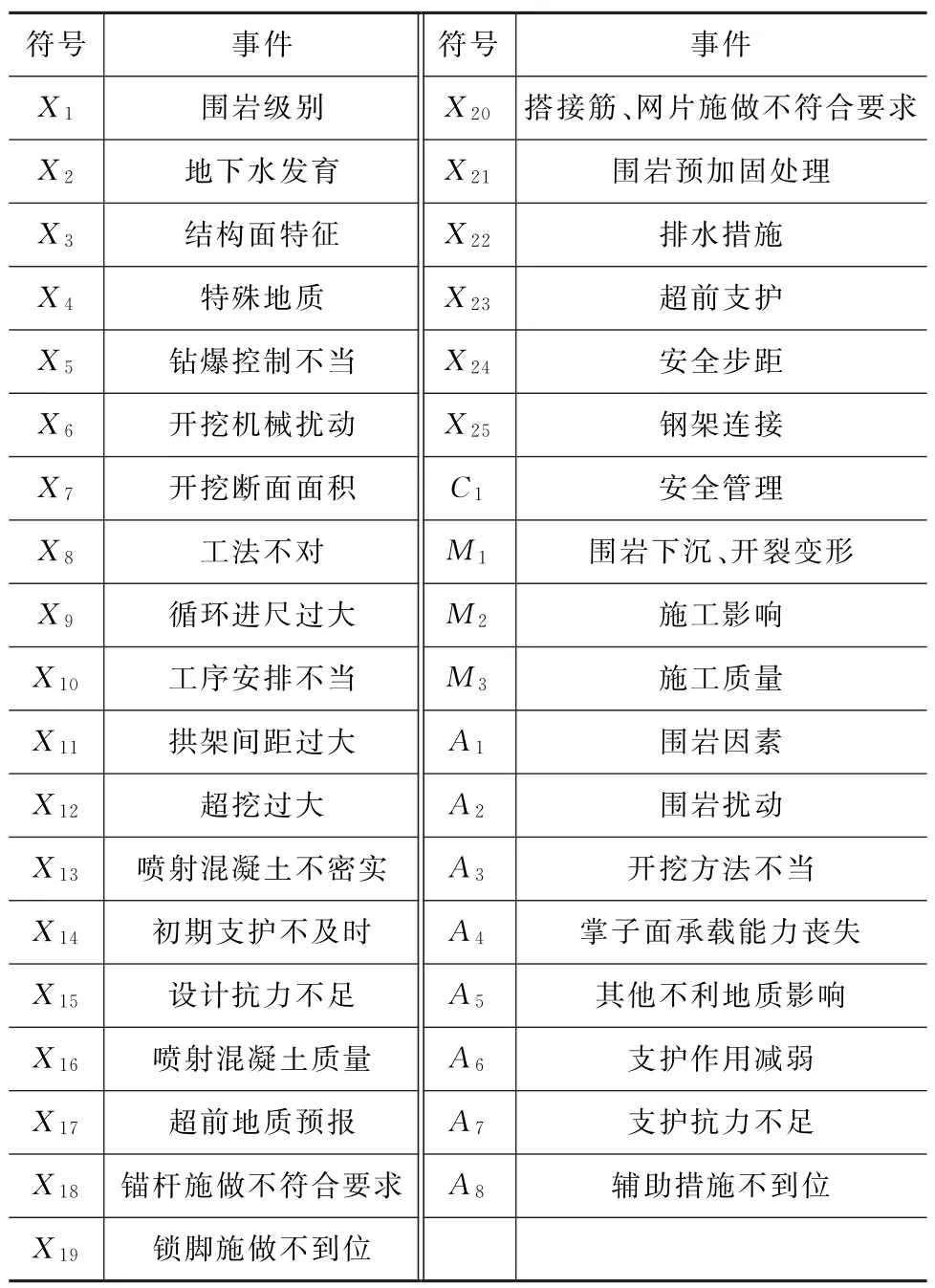
表2 事故树事件及符号

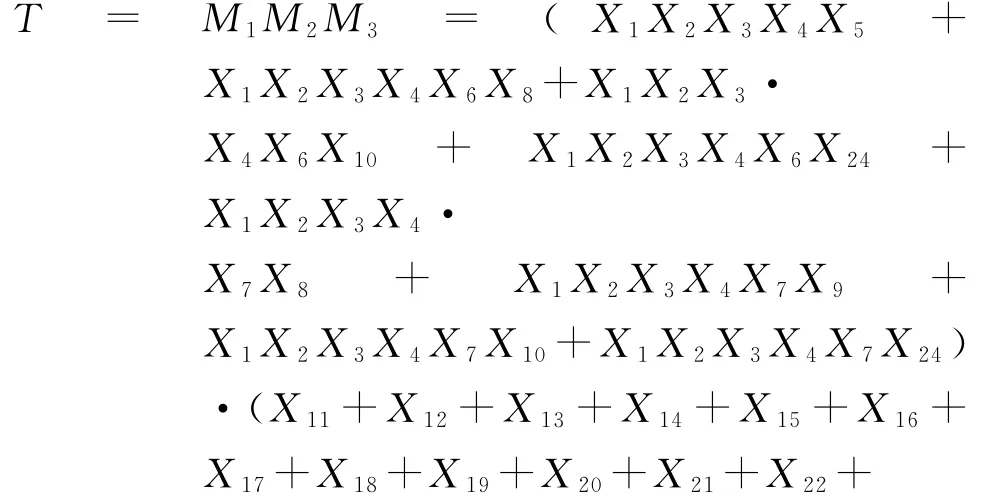
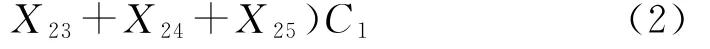
可知,该事故树有126个最小割集。

2.3 最小径集

根据最小割集与最小径集的对偶性,用布尔代数化简法求最小径集(对应的符号后加“'”)。

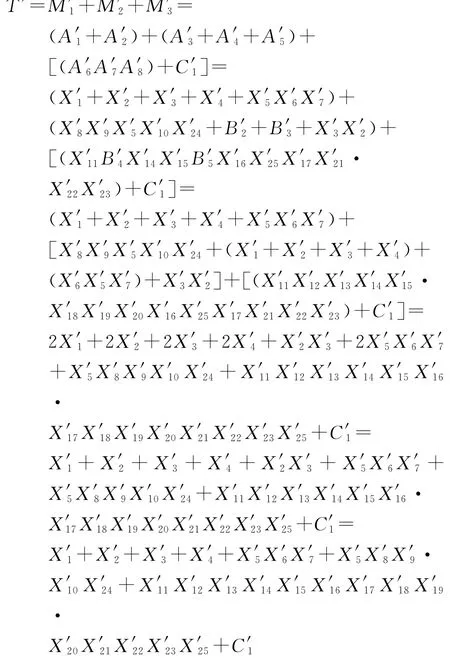
从化简结果可以看出,与事故树等效的成功树有8个最小割集。经对偶变换,得到事故树的8个最小径集,即{X1}、{X2}、{X3}、{X4}、{C1}、{X5, X6,X7}、{X5,X8,X9,X10,X24}、{X11,X12,X13, X14,X15,X16,X17,X18,X19,X20,X21,X22,X23, X25}。

所以用最小径集表示的隧道塌方事故树结构式为T=X1X2X3X4C1(X5+X6+X7)(X5+X8+X9+X10+X24)(X11+X12+X13+X14+X15+X16+ X17+X18+X19+X20+X21+X22+X23+X25)

综上可知,事故树模型的最小割集数远多于最小径集数,故使用最小径集进行塌方事件定性和定量分析。

3 定性分析

事故树的定性分析是依据事故树对所有事件只有发生(“1”)或不发生(“0”)两种状态进行逻辑计算,其目的是采用图论的方法检索出顶上事件发生的路径,给出顶上事件发生原因及各事件的影响程度。结构重要度是从事故树结构入手,分析各基本事件的重要程度,它是重要的定性分析途径,可通过最小割集或最小径集得到。

原事故树有8个最小径集,根据最小径集对25个基本事件进行结构重要度(Iφ)排序如下。

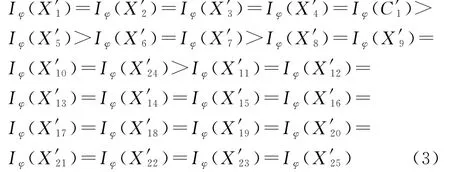
4 定量分析

4.1 隧道塌方发生概率计算模型

事故树的结构函数为

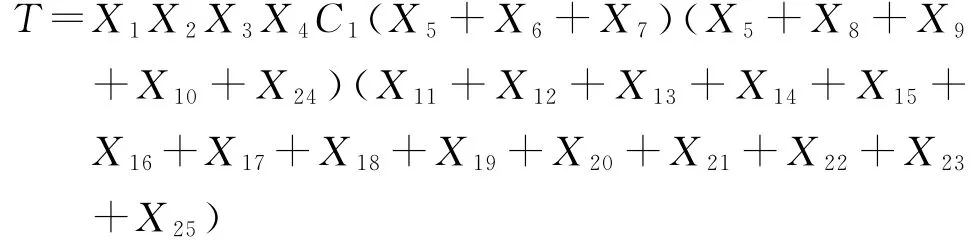
因此隧道塌方顶上事件发生的概率函数为

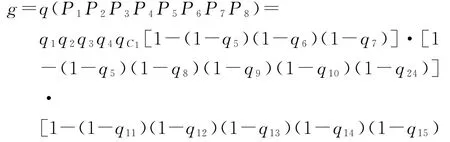
因为基本事件有重复,对式(4)进行展开并消掉重复事件Xi不发生的概率(1-qi),整理得隧道塌方发生概率的计算模型

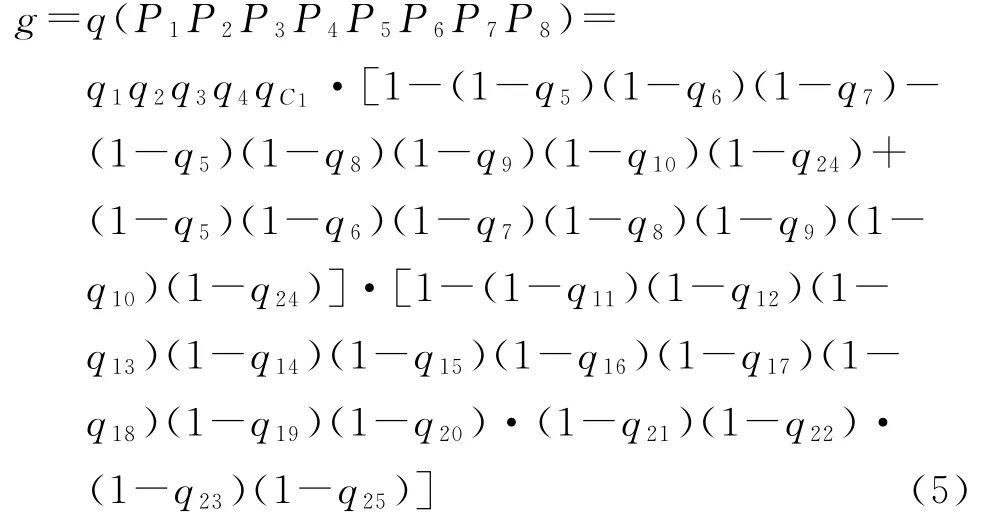
4.2 基本事件概率重要度分析

式(5)表明,隧道塌方事件发生概率是各基本事件发生概率的多元函数,各基本事件发生概率的变化对塌方事件发生概率的影响程度称为基本事件概率重要度。对多元函数求关于自变量qi的一次偏导,即可得出该基本事件的概率重要度系数计算模型

式中:Ig(i)为基本事件Xi的概率重要度系数;g为隧道塌方事件发生概率;qi为基本事件Xi的发生概率。

利用式(6)可计算出所有基本事件概率重要度系数,将计算结果从大到小进行排序,可得到导致顶上事件发生的基本事件的影响程度大小。

4.3 临界重要度分析

临界重要度系数从灵敏度和概率2个角度反映各基本事件的重要度。

式中:Cg(i)为基本事件Xi的临界重要度系数。

根据式(7)计算出所有基本事件临界重要度系数,将计算结果从大到小进行排序,可得到一个即考虑敏感度又考虑概率的各基本事件重要度排序。

5 工程实例分析

5.1 工程概况

兰渝铁路某隧道围岩主要为泥岩夹砂岩,多呈互层状分布,局部段拱部砂岩夹层增厚,以砂岩为主段落,掌子面有少量渗水,围岩稳定性较差。初期采用三台阶法施工,施工过程中进度缓慢,DK114+ 559~DK114+567段拱部发生塌方。

采用以下处置措施:施工方法由三台阶法改为CRD法(交叉中隔墙法);拱部超前小导管加密环向间距,每榀钢架施作1次;径向回填注浆,全环设置Φ42 mm注浆小导管,间距1 m×1 m;降水先行,采取中下台阶轻型井点及深井降水方案;加强支护强度及刚度;清退原有作业队伍,重新引进经验丰富、管理效率高的队伍。做出以上调整后,该隧道顺利度过塌方段,安全贯通。

5.2 事故树分析

5.2.1 定性分析

以结构重要度为指标,根据式(3)对实例事故树进行定性分析,利用径集计算结构重要度,并进行排序。

5.2.2 定量分析

顶事件发生概率是最重要的定量分析指标。在隧道施工期间,现场分别记录统计了三台阶施工和CRD施工中底事件的概率,三台阶法施工底事件的概率为0.006 225,采用CRD法施工底事件的概率为0.000 941。可见,采取CRD法后塌方发生概率明显降低,和模型结论一致。

6 结 语

(1)本文在分析隧道塌方相关数据及影响因素的基础上,建立了隧道塌方事故树模型。事故树模型表明,导致隧道塌方的途径越多,塌方事件发生的可能性就越大。

(2)从结构重要度可知I[X1]=I[X2]=I[X3] = I[X4]=I[C1]=0.667,因此这5个因素对塌方的影响较大,对预防塌方有重要意义;但前4个因素主要依靠辅助措施实现控制。

(3)依据事故树模型,采取措施前后隧道塌方的发生概率从0.006 225降至0.000 941。

[1] 刘科伟.公路隧道建造期塌方风险分析及控制的系统研究[D].长沙:湖南大学,2012.

[2] 李风云.隧道塌方风险预测与控制研究[D].长沙:中南大学, 2011.

[3] 吴学智,王 建,杨保全.某强倾倒变形体内浅埋偏压洞口段的隧道变形分析及处治技术研究[J].隧道建设.2015,35(7): 721-726.

[4] 王军涛,王海亮,杨 庆.城市硬岩隧道减振爆破直眼掏槽技术应用及实践[J].隧道建设,2014,34(6):564-568.

[5] 丰明海,何振宁.铁路隧道施工中围岩变形失稳工程地质问题[J].工程地质学报,2014,22(4):677-683.

[6] 何茂周.地铁盾构隧道穿越桩基综合处理技术[J].隧道建设, 2014,34(10):981-989.

[7] ALIABADIAN Z,SHARAFISAFA M,NAZEMI M.Numerical Analyses of Tunnel Collapse and Slope Stability Assessment Under Different Filling Material Loadings:A Case Study[J].Arabian Journal of Geosciences,2015,8(3):1229-42.

[8] 张 岭.隧道工程施工安全风险管理研究[D].石家庄:石家庄铁道大学,2013.

[9] 周建昆,吴 坚.岩石公路隧道塌方风险事故树分析[J].地下空间与工程学报,2008,4(6):991-998.

[10] 陈洁金,周 峰,阳军生,等.山岭隧道塌方风险模糊层次分析[J].岩土力学,2009,30(8):2365-2370.

[11] 曹文贵,翟友成,王江营,等.山岭隧道塌方风险的集对分析方法[J].中国公路学报,2012,25(2):90-99.

[12] 李风云.隧道塌方风险预测与控制研究[D].长沙:中南大学, 2011.

[13] 宓荣三.基于网络模糊综合评价的铁路隧道塌方风险分析研究[J].中国铁路,2011(3):46-49.

[14] 孙彦峰.理想点法在隧道塌方风险等级评价中的应用[J].隧道建设,2016,36(11):1310-1316.

[15] 夏 超,李 洁.基于集对分析的地铁隧道塌方风险评价[J].筑路机械与施工机械化,2016,33(4):112-116.

[16] 于咏妍.基于模糊层次分析法的隧道坍塌风险评估[J].交通科技,2016(5):111-114.

[责任编辑:杜敏浩]

Risk Assessment of Tunnel Collapse Based on Fault Tree Analysis

NAN Yu-hong,ZHAO Song,YANG Zheng-mao
(China Railway Academy Co.,Ltd.,Chengdu 611731,Sichuan,China)

Based on the investigation and analysis of the causes of common safety accidents in tunnel construction,the risk factors and dangerous environment around the tunnel were identified.The fault tree analysis method was used to establish the model for tunnel collapse,and the events of tunnel collapse were qualitatively and quantitatively analyzed.The structural importance sequence of the 26 basic events,the probability and the critical importance analysis method of tunnel collapse were acquired.In terms of the analysis on practical projects,the occurrence probability of the tunnel collapse is reduced from 0.006 225 to 0.000 941 after taking measures.

tunnel engineering;collapse analysis;fault tree analysis;probability model

U452.2

B

1000-033X(2017)07-0106-05

2017-01-12

中铁西北科学研究院创新项目(J2014003)

南宇宏(1973-),男,陕西渭南人,工程师,从事铁路、公路工程监理咨询工作。