几种加窗F F T算法谐波检测仿真比较

安徽理工大学电气与信息工程学院 王肖峰

几种加窗F F T算法谐波检测仿真比较

安徽理工大学电气与信息工程学院 王肖峰

对数字信号进行快速傅里叶变换，可得到数字信号的分析频谱。分析频谱是实际频谱的近似。傅里叶变换是对延拓后的周期离散信号进行频谱分析。如果采样不合适，某一频率的信号能量会扩散到相邻频率点上，出现频谱泄漏现象。为了减少频谱泄漏，通常在采样后对信号加窗。

海宁窗；海明窗；高斯窗；谐波分析

1 引言

在采用FFT对谐波进行检测分析时，一些误差是不可避免的，例如频谱泄漏以及栅栏效应。这是因为将连续的模拟信号转换成离散数字信号而导致的结果[1]。

所谓频谱泄漏，就是信号频谱中各谱线之间相互影响 ，使测量结果偏离实际值，同时在谱线两侧其他频率点上出现一些幅值较小的假谱。简单说来，造成频谱泄漏的原因是采样频率与信号频率不同步，造成周期采样信号的相位在始端和终端不连续。栅栏效应描述的是信号采样时只能得到采样点的信息，而忽略了采样间隔中数据信息的现象[2-5]。

频谱泄漏和栅栏效应，都会对FFT算法在信号处理时产生误差。针对频谱泄漏可以加大窗函数的宽度，相对的频域上就窄了，也就是泄露的能量就小了。栅栏效应，可以提高采样点，间隔小，频率分辨力高，被“挡住”或丢失的频率成分就会越少。

2 分别对几种窗函数进行仿真分析

图1所示为三种窗函数的波形图及其归一化曲线仿真。

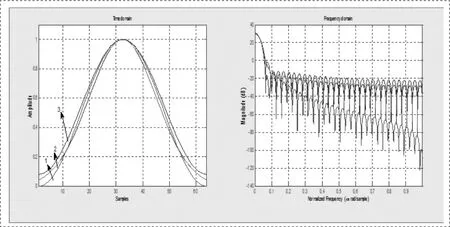
图1 N=64，几种窗函数的波形和归一化曲线

如图1所示，是采样点为64时，三种窗函数的归一化曲线。绿色线-海宁窗，红色-高斯窗，蓝色-海明窗。从图中可以看出，海宁窗的主瓣较窄，旁瓣小，能量较集中，所以海宁窗对信号的处理效果较好。同时采样点的多少对窗函数也有影响，采样点越多，窗函数的主瓣越窄，旁瓣越小。所以应在条件允许的情况下选用更多的采样数据进行信号分析。

在仿真实验时，分别对信号加不同的窗函数的FFT处理，原始信号为：

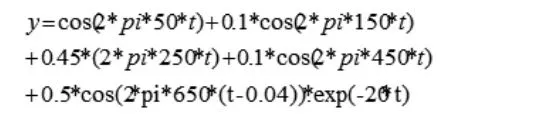
图2 原始信号波形及其频谱

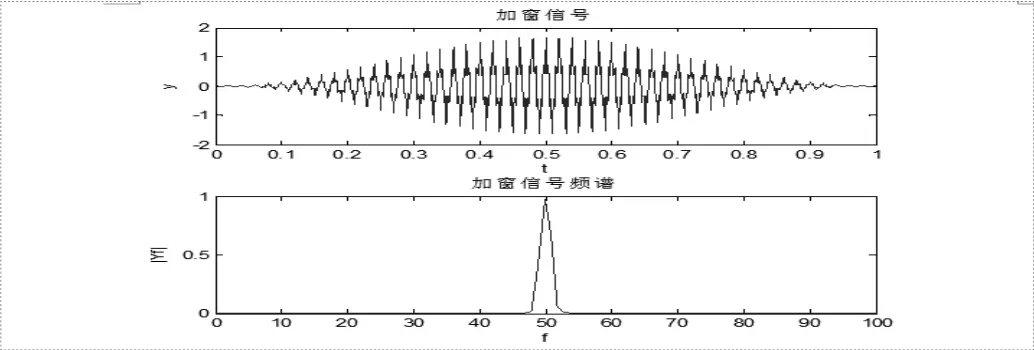
图3 加海宁窗信号波形及其频谱

图3所示为加海宁窗的仿真效果，从频谱上可以看出，主谱相对集中，旁瓣较窄，说明了加海宁窗对减少频谱泄漏具有很好的抑制效果。

3 总结

通过分析信号在采样时产生的频谱泄漏和栅栏效应等问题，提出了相应的解决办法。由图2和图3的对比可知，通过加海宁窗之后，可以看到其旁瓣变窄，主瓣能量集中，具有很好的效果。

由于对非同步采样序列进行FFT进行分析时存在栅栏效应和泄漏现象，使测量产生误差，无法满足谐波测量准确性的要求。因此采用加窗插值FFT算法，通过对信号加窗可以消除由泄漏现象引起的误差，通过插值算法可以减小由栅栏效应引起的误差。

[1]郑博．离散Fourier变换的算法分析研究[J]．重庆电子工程职业学院学报,2013,4:165-167．

[2]张杨,刘志刚．一种基于时频域多特征量的电能质量混合扰动分类新方法[J]．中国电机工程学报,2012,32(34):83-90．

[3]王丽霞,何正友,戴铭,等．一种电能质量扰动信号的分层识别新方法[J]．电力系统自动化,2009,33(24):65-69．

[4]Wang Q,Wang P,Kong L,et al．Novel Gas Concentration Measurements based on Harmonic Detection and a Broadband Light Source[J]．Instrumentation Science & Technology,2015,43(3):269-282．

[5]Chang G W,Chen C I,Teng Y F．Radial-Basis-Function-Based Neural Network for Harmonic Detection[J]．IEEE Transactions on Industrial Electronics,2010,57(6):2171-2179．

Comparison of Harmonic Detection in Several Windowed FFT Methods

WANG Xiao-feng
（School of electrical and Information Engineering，Anhui University of Science and Technology，Huainan Anhui 232001，China）

The digital signal is subjected to fast Fourier transform，and the spectrum of the digital signal can be obtained.The analysis spectrum is an approximation of the actual spectrum.Fourier transform is the spectral analysis of the periodic discrete signal after extension.If the sampling is not appropriate，a certain frequency of signal energy will spread to the adjacent frequency point，the phenomenon of spectrum leakage.In order to reduce the spectral leakage，usually after sampling the signal window.

Haining Window；Hamming Window；Gaussian Window；Harmonic Analysis