逆变型微网下垂控制器参数选择和稳定性分析

谷青发， 王 杰

(上海交通大学电子信息与电气工程学院， 上海 200240)



逆变型微网下垂控制器参数选择和稳定性分析

谷青发， 王 杰

(上海交通大学电子信息与电气工程学院， 上海 200240)

微网的动态稳定分析广泛采用特征分析法。微网孤岛运行时，多使用下垂控制方法来稳定其电压和频率。下垂控制器中下垂增益的选取会对微网系统的稳定性产生重要的影响。本文研究了状态矩阵中含有不确定参数的线性系统的稳定性分析方法，建立了微网采用下垂控制的小信号模型。利用提出的方法，分析了微网的小信号稳定性，并给出了系统为渐进稳定时下垂控制器下垂增益的范围。最后，通过模态相关因子的方法分析了系统稳定性与下垂增益的关系。算例结果验证了该方法的正确性。

微网； 逆变器； 下垂控制； 参数不确定； 稳定性

1 引言

随着能源危机和环境污染问题的加剧，能源生产方式和消费方式的变革势在必行。以新能源供给为主的分布式发电技术具有极大的应用潜力，但由于其并网存在诸多问题，无法被电力部门大规模接受。微网技术是实现分布式发电系统大规模应用和电网智能化的关键技术之一[1,2]。一般认为，微网是指由分布式电源(DG)、储能装置、电力电子变换装置、保护装置、负荷和监控系统组成的小型发配电系统，是一个能够实现自我控制、保护和管理的自治系统[3,4]。微网既可以并网运行，也可以孤岛运行。

微网中分布式电源大多通过逆变器产生交流电接入电网或给负荷供电，实现能量双向流动。当微网运行在孤岛模式时，为了稳定微网的频率和电压，逆变器的控制策略大多采用下垂控制方法。下垂控制的基本思想是通过微电源的有功和无功功率反馈分别调整系统的电压和频率，从而实现系统电压和频率的稳定。这种方法只需要采集本地信息，就地测量就地控制，可以减少因通信而产生的延时，增强系统控制的可靠性和准确性。

逆变器中下垂增益参数的选取会对微网系统的稳定性产生至关重要的影响，因此需要对其选取和微网稳定性的关系进行研究[5]。文献[6-9]考虑控制器和负荷网络的动态特性，建立了基于下垂控制的微网小信号模型，利用该模型计算系统状态矩阵特征根，分析了微网的稳定性。文献[10]将微网的稳定性分析分为小扰动稳定分析和暂态稳定分析，分别建立了不同电压等级的微网状态空间模型，算例结果表明不同电压等级的微网系统可以采用不同的模型进行稳定性分析。文献[11]建立了基于多变流器微网小信号模型，采用计算根轨迹的方法得到了微网中参数与稳定性的关系。文献[12]研究了一种基于二阶摄动理论的微网小干扰稳定性分析方法，利用该方法可以简便地计算出微网出现小扰动时系统状态矩阵的近似特征根，从而分析系统的稳定性。

文献[6-12]中建立了采用下垂控制的微网小信号模型，利用状态矩阵的特征根分析了微网稳定性与下垂增益、网络参数的关系。但是这些文献中下垂增益的值都是直接给出的，鲜有文献对于下垂增益参数的范围与微网系统稳定性之间的关系进行研究。当下垂增益为未知参数时，微网的状态矩阵中将含有不确定参数，尤其当矩阵维数过高时，通过求解状态矩阵特征根研究系统稳定性的方法将失效。针对此问题，本文研究了一种状态矩阵中含有不确定参数的线性系统的稳定性分析方法，建立了基于下垂控制的微网小信号模型，并利用提出的方法求解了使得含有不确定参数的系统稳定的下垂增益的范围，算例结果表明，当下垂增益位于该范围内时系统能够保持稳定。最后用模态相关因子法分析了下垂增益对于系统稳定性的影响，确定了影响系统稳定性的关键参数。

2 基于下垂控制的微网小信号模型

2.1 控制器小信号模型

逆变器下垂控制的基本原理如图1所示。

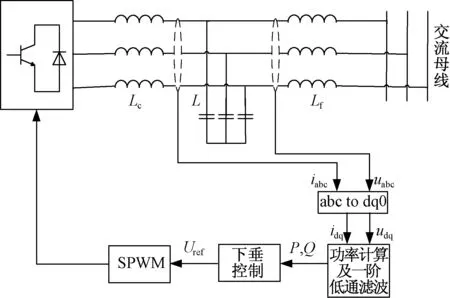
图1 逆变器下垂控制方框图Fig.1 Schematic of droop control

下垂控制器数学表达式为：

(1)

式中，m和n分别为逆变器角频率下垂增益和电压下垂增益；ωn和Vn分别为分布式电源参考角频率和参考电压幅值；ω和V分别为分布式电源的角频率和电压幅值；p和q分别为分布式电源输出的瞬时有功和无功功率；ωc为低通滤波器的截止频率。

将式(1)线性化可得：

(2)

在dq0坐标系下，分布式电源输出的电压相角和电压幅值为：

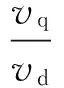
(3)

将式(3)在稳态运行点处Taylor展开并线性化可得：

(4)

式中

其中，vd0和vq0为dq0坐标系下分布式电源稳态运行点的值。

由于Δω(s)=sΔδ，可知：

(5)

dq0坐标系下，分布式电源电压的d轴和q轴分量为：

vd=vcosδ，vq=vsinδ

(6)

将式(6)在稳态运行点Taylor展开，线性化并求导可得：

(7)

整理式(2)～式(7)可得：

(8)

式中

2.2 电网络小信号模型

逆变型微网等效结构图如图2所示。其中两个分布式电源均采用下垂控制，同时给负荷供电。

图2 微网等效电路Fig.2 Equivalent circuit model of microgrid

图2所示的电网络状态方程为：

(9)

式中，RL和C分别为负载的等效电阻和电容。

分布式电源供给负荷的电流可表示为：

is=i1+i2

(10)

考虑到传输线路电阻率和电感率一般保持一定的比例[13]，可近似认为：

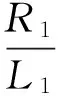
(11)

联立式(9)～式(11)可得：

(12)

式中，Rd=(R1+R2)/2;Ld=(L1+L2)/2。

式(12)经线性化和Park变换后，在dq0坐标系中，图2所示的电网络状态方程可表示为：

(13)

式中

X1=(Δω1,Δv1d,Δv1q,Δω2,Δv2d,Δv2q)T

X2=(Δvbd,Δvbq,Δisd,Δisq)T

其中，Δω1和Δω2分别为分布式电源1和2的角频率变化量。

图2中，分布式电源输出功率为：

(14)

整理式(14)，可得：

(15)

式中

将式(15)在稳态运行点处Taylor展开并线性化，可得：

(16)

式中

2.3 微网小信号模型

联立式(8)、式(13)和式(16)，可得微网小信号模型为：

(17)

式中

其中，Bi、Ci、Di和Ei(i=1,2)分别为第i个分布式电源对应的系数矩阵。

3 参数不确定线性系统的稳定性

3.1 系统描述

考虑以下状态矩阵中含有不确定参数的线性系统[14,15]：

(18)

式中，x∈Ω∈Rn，为n维状态向量，其中Ω为含x=0的某个邻域；εj为不确定参数；G为稳定阵，即G的特征根的实部均为负值。

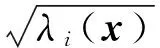
为简单起见，对每个固定的x∈Ω，记δM(U(x))为矩阵U(x)的n个奇异值中的最大值；如果QTQ=R，则记R1/2=Q。

由定义1可知，δM(U(x))即为矩阵U(x)的二范数，即

‖U(x)‖=δM(U(x))

(19)

3.2 系统稳定性分析

由于式(18)描述的系统中矩阵G是稳定阵，因此对任意n阶正定阵Q，必有唯一正定阵P，满足：

GTP+PG=-Q

(20)

对于式(18)描述的线性系统构造如下的Lyapunov函数：

V(x)=xTPx

(21)

由于P是正定阵，因此V(x)是正定函数，即V(x)>0。对V(x)求导可得：

(22)

(23)

式(22)和式(23)中正定矩阵Q为可调矩阵，其选取并不唯一，适当的选取Q可增大参数的鲁棒空间。利用式(23)中的条件不易求解参数的范围，为简化运算取Q=I，相应的P记为PI，即

GTPI+PIG=-Q

(24)

则式(23)可表示为：

(25)

进一步简化，式(25)可以表示为：

(26)

用式(26)可以方便地求出式(18)描述的系统为渐进稳定时参数εj的范围。由于正定阵Q的选取不唯一，当Q变化时，相应的参数εj的范围也会发生变化，但并不影响在求得的参数范围内系统的稳定性。

4 特征根与模态相关因子

特征根分析是电力系统小信号稳定性分析的基础。在控制理论中，状态矩阵的每一个特征根代表了系统的一种运行模态，而每一种运行模态与系统状态变量之间存在一定的关联性。

定义2：对矩阵W的任一特征根λi，满足方程：Wui=λiui，WTvi=λivii=1,2,...,n，的n维非零向量ui和vi分别称为矩阵W关于特征根λi的右特征向量和左特征向量。

在式(18)描述的系统中，状态矩阵特征根λi的右特征向量的第k个分量uki反映了状态量xk对λi的“可观性”；而左特征向量的第k个分量vki则反映了状态量xk对λi的“可控性”[16]。因此，定义uki和vki的积pki为相关因子，即

pki=ukivki

(27)

相关因子pki反映了第i个模态中第k个状态变量的相对参与程度，其值越大，表示状态变量参与程度越高，对系统的影响越大。利用相关因子可以分析影响系统模态的关键因素，进而通过调整关键因素改善系统的稳定性。

5 算例分析

5.1 系统稳定性分析

电网络和控制器各部分参数见表1。

表1 微网和控制器参数Tab.1 Parameters of microgrid and controller

采用第2节建立的小信号模型，可得微网小信号模型状态方程为：

(28)

式中，A0，K1，K2∈R10×10，为常量方阵。

利用式(26)可求得该系统为渐进稳定时下垂增益的范围，如图3所示。由图3可知，当下垂增益m和n位于直线和x轴及y轴包围的区域时，系统状态矩阵所有特征根的实部均小于0，系统能够保持稳定。由于式(20)中正定阵Q的取法并不唯一，不同的Q对应的参数范围也会发生相应的变化，当下垂增益的取值位于该稳定域内时，能够保证系统为渐进稳定。

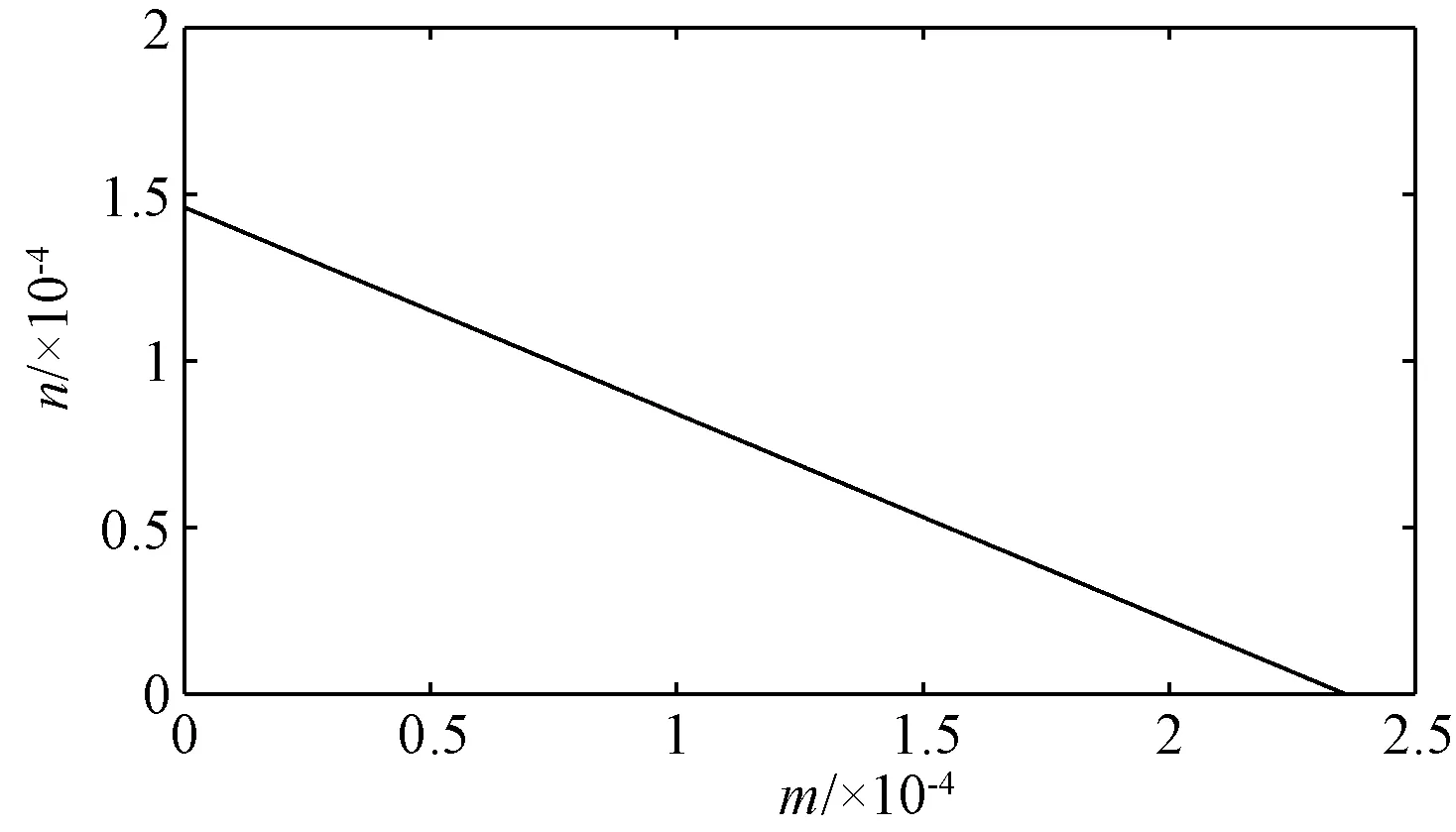
图3 系统参数稳定域Fig.3 Stability region of system parameters

为验证上述结论的正确性，任意选取稳定域中的两点m=10-4和n=2×10-5及m=5×10-5和n=10-4，计算系统的小信号状态矩阵，求出全部特征根，结果分别见表2和表3。

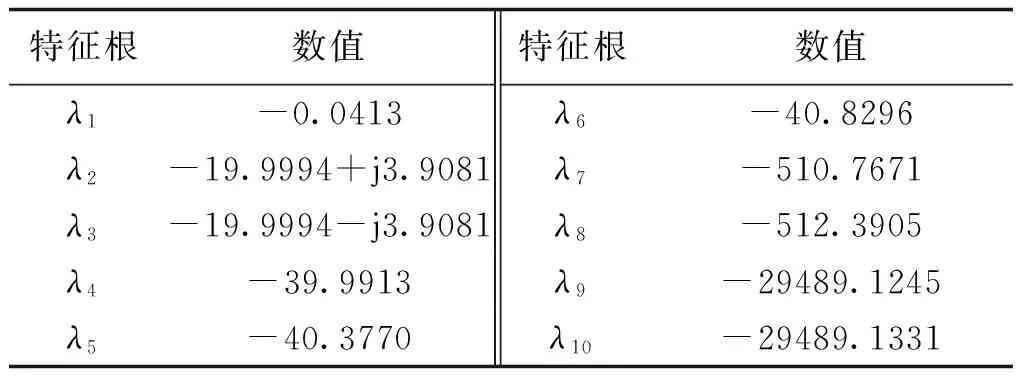
表2 m=10-4和n=2×10-5时状态矩阵特征根Tab.2 Eigenvalues of state matrix when m=10-4 and n=2×10-5

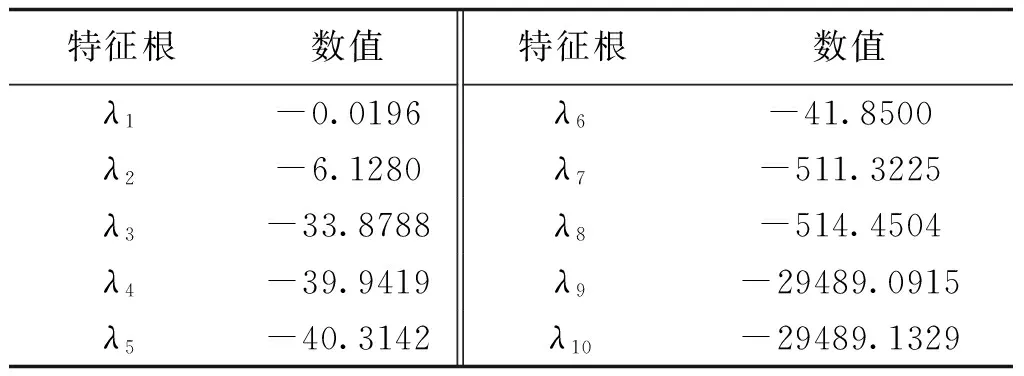
表3 m=5×10-5和n=10-4时状态矩阵特征根Tab.3 Eigenvalues of state matrix when m=5×10-5 and n=10-4

由表2和表3可以看出，当下垂增益参数m和n位于稳定域内时，状态矩阵的所有特征根的实部均位于虚轴的左侧，系统能够保持小信号稳定。

选取稳定域外的两点m=2.5×10-4和n=2×10-4及m=10-4和n=1.4×10-3，计算系统的状态矩阵，求出其全部特征根，结果见表4和表5。

表4 m=2.5×10-4和n=2×10-4时状态矩阵特征根Tab.4 Eigenvalues of state matrix when m=2.5×10-4 and n=2×10-4

由表4可知，系统状态矩阵的特征根的实部均小于0，系统稳定；由表5可以看出，系统状态矩阵的特征根λ1实部大于0，系统失稳。因此，当选取的下垂增益落在稳定域外时，除个别点能够保持系统稳定外，系统基本表现为失稳。该结论与第3节的分析结果一致。同时，由表4和表5可以看出，选取的点离稳定域越远，系统的稳定性越差。

5.2 模态相关因子分析

电力系统中，一般选取实部靠近虚轴的主特征值进行分析。选取稳定域内一点m=10-4和n=2×10-5时系统状态矩阵的特征根λ1=-0.0413作为主导特征根，计算相关因子模值，结果见表6。

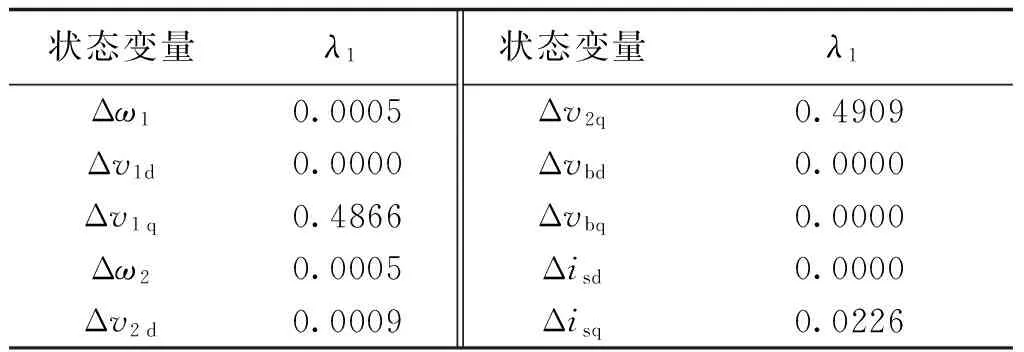
表6 主导特征根的相关因子Tab.6 Participating factors of leading eignvalue

由表6可以看出，特征根λ1主要与状态变量Δvq有关。下垂控制器中影响逆变器输出电压的是下垂增益n的变化。因此，控制器参数中电压下垂增益n对主导特征根λ1的影响较大，进而影响系统的稳定性。

为验证上述结论的可靠性，保持角频率下垂增益m不变(m=10-4)，电压下垂增益n从2×10-5增大到1.5×10-3时，特征根的变化轨迹如图4中箭头方向所示。

图4 主导特征根随下垂增益n变化轨迹Fig.4 Track of leading eignvalue when droop gain n changes

由图4可以看出，随下垂增益n的增大，主导特征根的实部逐渐向虚轴方向靠近，系统稳定性变差。当下垂增益n增大到一定程度(n=1.4×10-3)，主导特征根的实部将大于0，系统失稳。因此，当下垂增益n变化时，对主导特征根的影响较大，该结论与相关因子的分析结果一致。

6 结论

本文建立了一种状态矩阵中含有不确定参数的线性系统的稳定性分析方法，使用该方法可以方便地求出线性系统为渐进稳定的参数范围。其次，建立了基于下垂控制的微网小信号模型，并利用近似处理，简化了模型。利用提出的方法分析了系统为渐进稳定时下垂增益的范围。仿真结果表明，在求得的下垂增益范围内，系统能够保持渐进稳定性。因此，所提出的分析方法能够为下垂控制器中下垂增益的选取提供一定的指导意义。但是，由于算法中的正定矩阵Q的选取不唯一，使得系统稳定与不稳定的参数之间没有确定的界限，这一问题还有待进一步深入的研究。最后，利用模态相关因子法分析了系统稳定性与下垂增益的关系，结果表明下垂增益越大，系统稳定性越差，当下垂增益增大到一定程度，系统会失稳。因此，合理的选择下垂增益参数对于采用下垂控制的微网的系统稳定性至关重要。

[1] 张建华, 苏玲, 刘若溪，等(Zhang Jianhua, Su Ling, Liu Ruoxi, et al.). 逆变型分布式电源微网小信号稳定性动态建模分析(Small-signal dynamic modeling and analysis of a microgrid composed of inverter-interfaced distributed generations) [J]. 电力系统自动化(Automation of Electric Power Systems), 2010, 34(22): 97-102.

[2] 冯建周,王晓寰,张纯江，等(Feng Jianzhou, Wang Xiaohuan, Zhang Chunjiang, et al.). 基于频率恢复控制的逆变器主动同步策略研究(Active synchronization control of inverter based on frequency recovery control)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy),2016,35(6):7-12.

[3] 栗赛男,马建伟,孙芊，等(Li Sainan, Ma Jianwei, Sun Qian, et al). 考虑不确定出力的微网内分布式发电和储能的容量配置(Configuration optimization of capacity of distributed generation and energy storage in microgrid considering uncertain output)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy),2016,35(8):21-28.

[4] 张庆海, 彭楚武, 陈燕东，等(Zhang Qinghai, Peng Chuwu, Chen Yandong, et al.). 一种微电网多逆变器并联运行控制策略(A control strategy for parallel operation of multi-inverters in microgrid) [J]. 中国电机工程学报(Proceedings of the CSEE), 2012, 32(25): 126- 132, 18.

[5] 肖朝霞(Xiao Zhaoxia). 微网控制及运行特性分析(Control and operation characteristic analysis of a micro grid)[D]. 天津：天津大学(Tianjin: Tianjin University), 2009.

[6] Shi H，Zhuo F，Hou L, et al. Small-signal stability analysis of a microgrid operating in droop control mode[A]. 2013 IEEE ECCE Asia Downunder[C]. 2013. 882-887.

[7] 徐青山, 孙鄞, 丁茂生，等(Xu Qingshan, Sun Jin, Ding Maosheng, et al.). 采用下垂控制的微电网小干扰稳定性分析(Small-signal stability analysis of micro-grid with inverters employing droop control) [J]. 华南理工大学学报(自然科学版) (Journal of South China University of Technology (Natural Science Edition)),2013, 41 (12): 56- 62, 69.

[8] 张建华, 苏玲, 刘若溪，等(Zhang Jianhua, Su Ling, Liu Ruoxi, et al.). 逆变型分布式电源微网并网小信号稳定性分析(Small-signal stability analysis of grid-connected microgrid with inverter-interfaced distributed resources)[J]. 电力系统自动化(Automation of Electric Power Systems), 2011,35(6): 76-80, 102.

[9] 徐青山, 孙鄞, 丁茂生，等(Xu Qingshan, Sun Jin, Ding Maosheng, et al.). 采用下垂控制的微电网小干扰稳定性分析(Small-signal stability analysis of micro-grid with inverters employing droop control) [J]. 华南理工大学学报(自然科学版) (Journal of South China University of Technology (Natural Science Edition)),2013, 41 (12): 56-62, 69.

[10] 肖朝霞, 赵倩宇, 方红伟(Xiao Zhaoxia, Zhao Qianyu, Fang Hongwei). 逆变型微网状态空间方程的分析与建立(Analysis and establishment of state-space equations for inverter-interfaced microgrid) [J]. 电力系统自动化(Automation of Electric Power Systems), 2015, 39(2): 39-45.

[11] 马添翼, 金新民, 黄杏(Ma Tianyi, Jin Xinmin, Huang Xing). 含多变流器的微电网建模与稳定性分析(Modeling and stability analysis of microgrid with multiple converters) [J]. 电力系统自动化(Automation of Electric Power Systems), 2013, 37(6): 12-17.

[12] 彭跃辉, 杨耀, 马静，等(Peng Yuehui, Yang Yao, Ma Jing, et al.). 区间不确定信息下微网小干扰稳定性分析方法(Small-signal stability analysis of microgrid under interval uncertain) [J]. 华北电力大学学报(自然科学版) (Journal of North China Electric Power University (Natural Science Edition)), 2014, 41(5): 35-40.

[13] Tahim A P N, Pagano D J，Lenz E，et al. Modeling and stability analysis of islanded DC microgrids under droop control[J]. IEEE Transactions on Power Electronics, 2015, 30(8): 4597-4607.

[14] 严星刚, 井元伟, 张嗣瀛(Yan Xinggang, Jing Yuanwei, Zhang Siying). 一类参数不确定非线性系统的鲁棒稳定性(Robust stability for a class of nonlinear systems with uncertain parameters) [J]. 控制理论与应用(Control Theory and Applications), 1996, 13(3): 395-399.

[15] 胡庭姝，施颂椒(Hu Tingshu, Shi Songjiao). 状态矩阵中含不确定参数的系统的鲁棒性分析(Robust analysis for systems with uncertain parameters in state matrix) [J]. 控制理论与应用(Control Theory and Applications), 1992, 9(5): 533-537.

[16] 倪以信，陈府孙，张柬霖(Ni Yixin, Chen Fusun, Zhang Jianlin)．动态电力系统的理论与分析(Theory and analysis of dynamic power system )[M]．北京：清华大学出版社(Beijing: Tsinghua University Press)，2002．

Droop controller parameter selection and stability analysis for inverter-interfaced microgrid

GU Qing-fa, WANG Jie

(School of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

Eigen-analysis is widely used in dynamic stability analysis of power system. And droop control method is used to stabilize the voltage and frequency under islanding modes of microgrid. The selection of droop gain of droop controller will have great influence on system stability. This paper analyzes the stability of the state matrix containing uncertain parameters of the linear system, and establishes the small-signal model of microgrid under droop control mode. With the proposed method, the small-signal stability of micro-grid is analyzed. In such context, the dropping gain range is given when the system is asymptotically stable. Finally, the relationship between system stability and droop gain is analyzed through modal participating factor method. The numerical example demonstrates the validity of the method.

microgrid; inverter; droop control; uncertain parameter; stability

2016-10-12

国家自然科学基金项目(61374155)、 高校博士点专项科研基金项目(20130073110030)

谷青发(1992-)， 男， 河南籍， 硕士研究生， 研究方向为电力系统稳定分析与控制； 王 杰(1960-)， 男， 江苏籍， 教授， 博导， 研究方向为复杂系统非线性控制、 自适应控制、 鲁棒控制、 电力系统非线性控制与稳定分析。

10.12067/ATEEE1610020

1003-3076(2017)07-0034-07

TM721