基于经验模态分解和最小二乘支持向量机的溶氧预测
2017-08-30曹伟建秦益霖顾玉宛
宦 娟, 曹伟建, 秦益霖,2, 顾玉宛
(1 常州大学信息科学与工程学院,江苏 常州213164; 2 常州旅游商贸高等职业技术学校,江苏 常州213032)
基于经验模态分解和最小二乘支持向量机的溶氧预测
宦 娟1, 曹伟建1, 秦益霖1,2, 顾玉宛1
(1 常州大学信息科学与工程学院,江苏 常州213164; 2 常州旅游商贸高等职业技术学校,江苏 常州213032)
养殖池塘中溶氧(DO)与鱼、蟹等水产品的生长有着十分密切的关系。为了提高DO的预测精度和有效性,提出了一种基于经验模态分解(EMD)和自适应扰动粒子群优化最小二乘支持向量机(LSSVM)的组合预测模型。首先将DO时间序列通过EMD分解成若干分量,接着对各个分量进行相空间重构,在相空间中用LSSVM对各分量进行建模预测,并使用自适应扰动粒子群算法对LSSVM的超参数进行优化,采用单点迭代法进行多步预测。结果显示:该模型与单一LSSVM预测模型相比,具有良好的预测效果。预测未来4 h DO值时,各项性能指标误差均方根(RMSE)、平均相对误差均值(MAPE)和平均绝对误差(MAE)三项指标分别降低了13.4%、11.3%和1.8%;预测未来24 h DO值时,三项指标分别降低了12.9%、12.1%和2.7%。研究表明:该组合模型可有效提取DO序列特性,具有较高的预测精度和泛化性能。
溶氧预测;经验模态分解;最小二乘支持向量机;自适应粒子群算法;单次迭代法
信息技术已经成为现代水产养殖可持续发展的重要支撑,其在水产养殖智能投饲、疾病监测诊断以及水质监测、预测和预警等方面得到了广泛运用。溶氧(DO)是水产品生存的关键水质参数之一,反映出养殖水质的变化,水质的好坏直接影响水生动物的生长及其产品品质[1-2]。准确的DO预测具有十分重要的经济价值和现实意义。DO受物理因素、化学因素、生物因素以及人为因素的影响。国内外许多研究学者提出一些方法进行DO预测,如模糊推理模型[3]、灰色系统方法[4]、贝叶斯模型[5]、神经网络方法[6-7]和支持向量机[8-9]。其中最小二乘支持向量机(LSSVM)[10]是支持向量机的一种扩展,具有计算复杂度低、鲁棒性强、收敛精度较高、非线性拟合能力较好等特点。如果只使用最小二乘支持向量机建立预测模型,针对DO时间序列的非线性部分能进行比较好的拟合,然而在一定程度上DO的非平稳性却会对预测结果产生较大影响。从目前的研究成果看,以上所述的单一预测模型虽然有一定的优势,但预测误差比较大,无法满足对DO预测的更高要求。而组合预测模型的提出符合高精度DO预测的发展方向。
经验模态分解(EMD)是一种新型自适应信号时频处理方法[11],它完全不用考虑基函数,是根据数据信号本身的特征来进行分解的。对于处理非线性、非平稳的数据有着很好的作用。EMD 算法使用简单方便,有很快的分解速度,能够较好地捕捉不同尺度下的特征信息,具有多分辨特性,同时能克服小分解中需要选取小波基、确定分解尺度的困难。该算法已经在多个领域有了成功的应用,如:构建基于EMD和ELM的组合模型预测育苗水温[12];集合经验模态分解(EEMD)和人工蜂群算法组合模型预测pH[13],EEMD是针对EMD方法的不足,提出了一种噪声辅助数据分析方法。借鉴前人的研究,提出了采用EMD和LSSVM的组合模型预测DO值。
1 数据来源及方法
1.1 数据采集
选取溧阳市埭头黄家荡特种水产养殖场为试验区域。养殖场占地面积153 hm2,建有池塘循环水系统,配备DO传感器、增氧泵、无线监控系统等现代化渔业装备。养殖环境数据来自于水产养殖远程无线监控系统,每小时在线采集一次数据,选用2017年4月27日至5月2日共6 d的144个数据,选取前120个数据作为训练数据,后24个数据作为测试数据。
1.2 经验模态分解
EMD算法目的在于将性能不好的信号分解成一系列包含了原信号不同时间尺度局部特征信号的本征模函数(Intrinsic Mode Function,IMF)和一个趋势量Res,且IMF必须满足两个条件:信号的极大值和极小值点的个数与过零点的数目恰好相等,或者是相差小于等于一个;由局部极大值构成的上包络线和由局部极小值构成的下包络线的均值为零[10]。
对选定的DO时间序列x(t)进行经验模态分解,其步骤如下[14]:
第一步:确定整个DO时间序列的所有极大值和极小值,采用三次样条函数对极大值点和极小值点进行拟合,组成上包络线和下包络线,计算出上、下包络线的均值,记为n1(t)。将时间序列x(t)与n1(t)的差值,记为z1(t),t表示时间,即:
z1(t)=x(t)-n1(t)
(1)
第二步:判断z1(t)是否满足IMF的条件,如果满足,记b1(t)=z1(t),b1(t)就是时间序列x(t)的第一个IMF分量,如果不满足,则将z1(t)作为原始序列x(t)再重复第一步,直到经过k次后得到满足IMF条件的差值zk(t),记b1(t)=zk(t)。
第三步:用原始的时间序列减去b1(t),得到余项r1(t),即:
r1(t)=x(t)-b1(t)
(2)
再将r1(t)作为x(t)重复上述步骤,可以陆续得到其余的IMF和一个趋势量rn(t)。DO时间序列x(t)分解为如下形式:
(3)
1.3 最小二乘支持向量机
最小二乘支持向量机(LSSVM)支持向量机(SVM)的改良和发展[15], 对于非线性时间序列,LSSVM对其进行预测,它的回归问题可以描述为,对于给定的样本集{xi,yi},i=1,2,…,N,设其回归函数为:
f(x)=WTφ(x)+b
其中φ(x)为处理非线性问题的核函数,可将输入空间映射到高维特征空间[16-17]。将上述回归问题表示为约束优化问题。
(4)

(5)
通过对w,b,e,a求偏导数,化简后可得,
(6)
式中:Ψki=K(xk,xi),k,j=1,2,3,…,l,是核函数矩阵;C是正则化参数,a=[1,…,l];Y=[y1,…,yl];通过求解式(6),最后可以得到LSSVM的决策函数为
(7)
1.4 自适应扰动粒子群算法
运用改进的粒子群算法对LSSVM参数进行优化,克服粒子群早熟、局部最优等缺点,从而降低预测风险。粒子群算法(PSO)一开始先初始化一组随机解,然后所有粒子跟随当前的最优粒子在解空间中搜索,即通过迭代找到最优解。设d维搜索空间中的第i个粒子的位置和速度分别为Xi=(xi,1,xi,2,…,xi,d)和vi=(vi,1,vi,2,…,vi,d),每一次迭代时,粒子跟踪两个最优解来自我更新,第一个就是个体极值pbest,Pi=(pi,1,pi,2,…,pi,d),另一个则是全局最优解gbest,Pg,粒子通过式(8)和式(9)来更新自己的速度和位置。
vi,j(t+1)=wvi,j(t)+c1r1[pi,j-xi,j(t)]+c2r2[pg,j-xi,j(t)]
(8)
xi,j(t+1)=xi,j(t)+vi,j(t+1)
(9)
式中:w—权重系数;c1,c2—正学习因子;r1,r2—0到1之间的均匀分布随机数;j=1,2,…,d。
为了避免粒子群算法自身的早熟收敛问题,使用自适应扰动粒子群算法(ADPSO)[10,18]。在整个运行过程中,所有粒子都在寻找最优解,当接近极值时,粒子的速度降为零而停止运动,此时算法就陷入局部极值。因此,根据种群中粒子所在的位置就能判断种群是否陷入早熟。设定种群规模大小为M,当前群体平均适应度为favg,群体适应度方差d2可以定义为式(10),其中,fe为粒子e的适应度,f为归一化定标因子,用来限制适应度方差,f的值可由式(11)得到。
(10)
(11)
不同粒子的适应度会随着算法迭代次数的增加而越来越接近,因此,群体适应度方差d2就会
越来越小。d2越小说明群体中粒子越聚集,群体就越接近收敛。当d2小于给定阈值η时,种群就会陷入局部最优。此时,要对粒子进行扰动,让其继续搜索新的位置。粒子位置更新公式可修改为
(12)
式中:θ—扰动因子,是0到1之间的随机数,t为步数。
2 试验与结果
2.1 算法实现
基于EMD和自适应扰动粒子群算法优化LSSVM的溶氧组合预测模型,建模流程如图1所示。其步骤如下。
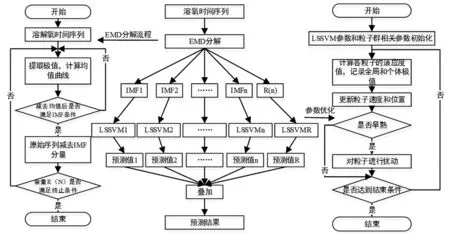
图1 基于 EMD-LSSVM 的溶氧预测流程图
(1)DO时间序列经验模态分解。将组成的DO时间序列经过经验模态分解,分解成IMF1,IMF2,IMF3,IMF4这4个分量和一个Res余项(图2)。

图2 DO时间序列 EMD 分解结果
(2) 数据归一化处理。将分解出来的各组数据xi采用最大最小法如式(13)进行归一化处理,从而减少因数据的量纲不同而影响预测模型。

(13)
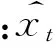
(3)相空间重构。根据周期性确定嵌入维数和延迟时间,对输入向量进行相空间重构。可观察DO时间序列存在周期性(周期为24),确实嵌入维数为24,延迟时间为1。根据公式(14)、(15)构造输入向量X(k),输出向量Y(k),其中D为嵌入维数,τ为延迟时间。
X(k)=[x(k),x(k+τ),…,x(k+(D-1)τ)]
(14)
Y(k)=x(k+D)
(15)
(4)核函数的选择。在每个LSSVM预测模型中,核函数的选择至关重要。RBF核可以处理系统内难以解析的规律性,具有良好的泛化能力和很快的学习收敛速度。所以本文选择RBF核作为核函数,其函数表达式如下式(16)所示。
(16)
式中:σ—宽度参数。将此式带入式(7)可以得到LSSVM的决策函数为
(17)
(5)参数优化。对粒子群算法进行初始化。设定种群数目为40,进化代数为300,加速度常数c1,c2都为2,适应度阀值为0.001。采用改进的粒子群算法对LSSVM模型中的惩罚参数C和宽度参数σ进行组合优化。以最小均方差函数(MSE)作为目标函数F,通过优化算法寻找F的最优值,以获取C和σ的最优组合。其表达式如公式(18)。

(18)

将求得的参数C和σ代入式(6),可以求得b和ai,再将这两个参数代入式(17),得到LSSVM回归估计函数表达式,对未来某个时刻的DO时间序列分量的值进行预测。
(6)单次迭代法。对每个分量的预测结果进行叠加,可获得下一个时刻的DO预测值。因为LSSVM只能实现单步预测,即一次只能得到一个预测值,运用单点迭代法实现多步预测,即预测未来24 h的DO值,其原理是利用预测值代替真实值作为预测输入向量的元素来获取下一个时刻的预测值。
(7)误差分析。选用误差均方根(RMSE),平均相对误差均值(MAPE)和平均绝对误差(MAE)作为评价指标。

(19)
(20)

(21)
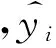
2.2 结果
采用本文建模方法得到的各分量相应的 LSSVM 参数C和σ2见表1。
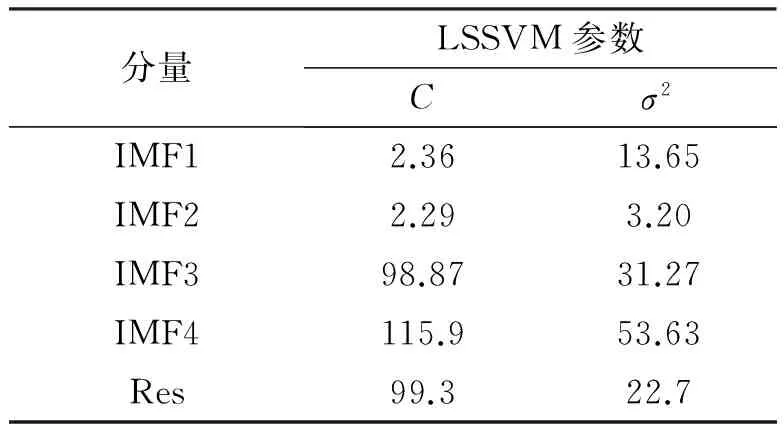
表1 各分量LSSVM参数
为了评估EMD-LSSVM预测模型的性能,将单一的LSSVM与EMD-LSSVM进行比较,两种模型采用相同的测试集,预测结果如图3所示。从图中可以直观地看到EMD-LSSVM的预测曲线与真实值曲线接近,而单一的LSSVM预测曲线较远,由此表明EMD-LSSVM的预测较为精准。

图3 EMD-LSSVM与单一LSSVM的预测值
为了进一步对比研究,表2给出了1 d不同时刻的实测值:EMD-LSSVM模型的预测值,单一LSSVM的预测值以及计算出的绝对百分比误差。从表2可以看出,EMD-LSSVM的预测结果,其误差比单一LSSVM预测结果的误差小,说明EMD-LSSVM具有较高的预测精度。
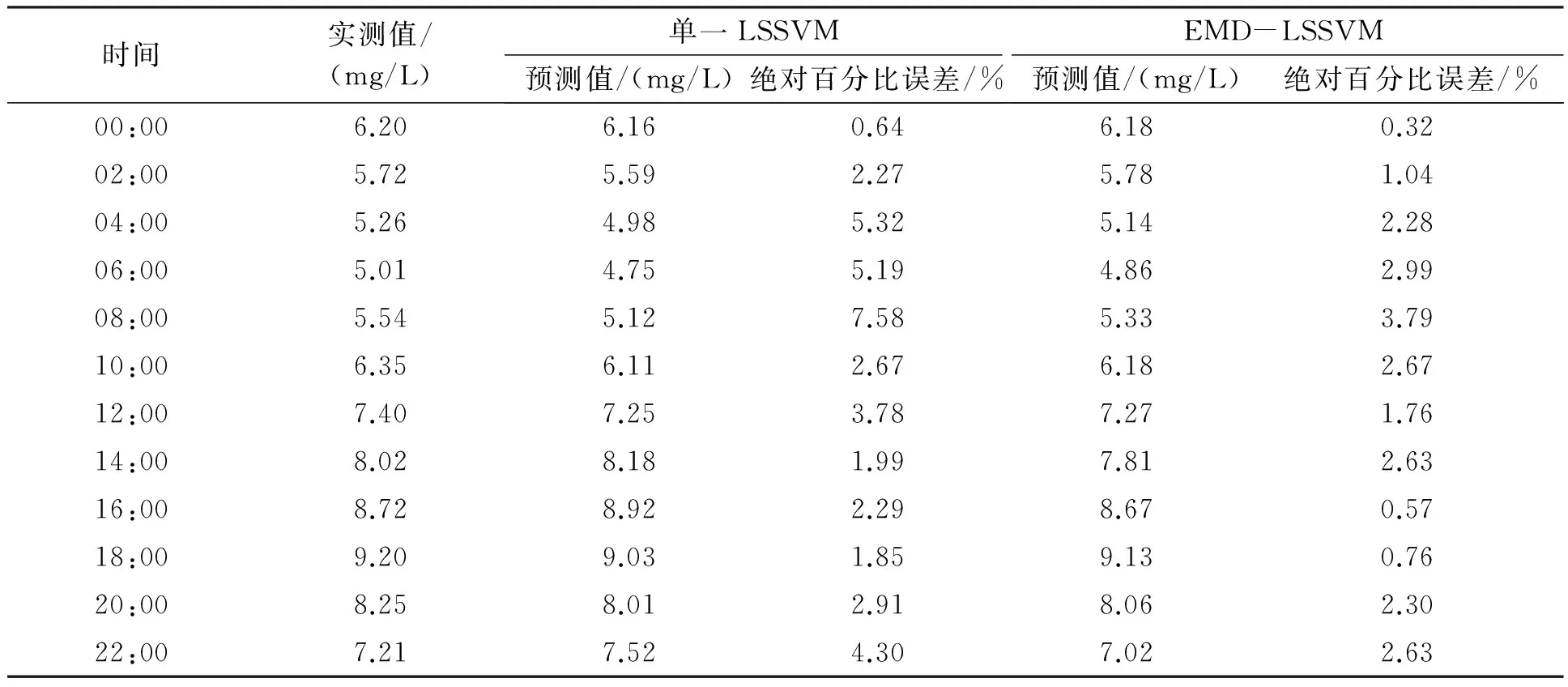
表2 预测值及绝对百分比误差
为了更加客观精确地评价预测精度,本文计算出2种预测模型的误差均方根(RMSE)、平均相对误差均值(MAPE)和平均绝对误差(MAE)3种评价指标,预测未来4 h和24 h的预测误差见表3。

表3 预测未来4 h和24 h误差指标
由表3可知,在相似的前提条件下,预测4 h DO值时,EMD-LSSVM与单一的LSSVM相比,评价指标RMSE、MAE、MAPE分别降低了13.4%、11.3%、1.8%;预测24 h DO值时,分别降低了12.9%、12.1%、2.7%。各项误差指标证明了EMD-LSSVM的组合预测模型的可行性,预测精度要高于单一的LSSVM预测模型。EMD-LSSVM模型可以对DO值进行有效预测,在一定程度上能够为水产养殖DO调控提供科学支撑。
3 讨论
由实验分析可知:(1)未经过EMD分解的LSSVM模型预测精度比EMD-LSSVM模型低。DO时间序列经过EMD分解后,降低了DO时间序列的非平稳性,减少了不同尺度信息间的相互影响,进一步挖掘和利用了DO序列的特征信息,提高了组合预测性能。(2)将改进的粒子群优化算法运用到本文的组合预测模型中,克服了组合权重确定过程中人为因素的影响,实验表明改进的粒子群算法可避免过早陷入局部最优,有比较好的自适应能力,是一种较好的组合权重寻优算法。(3)模型预测4 h的精度要比预测24 h的精度要高,参考相关文献[19]、文献[20],这是由于多步预测采用的是单点迭代法,一开始预测到的值在输入向量中占比不大,越往后预测值占比就越来越多,导致精度快速下降。(4)组合预测模型与单一的LSSVM相比具有先进性,可以为其他方向的模型建立提供有效参考。(5)在室外水产养殖场中,天气变化对DO会产生很大影响,在接下来的研究中,参考相关文献[6],根据天气的变化和晴、雨、阴、多云等天气状况,构造相似日DO时间序列,进一步优化本文提出的EMD-LSSVM模型,提高预测精度。此外,温度、pH、氨氮、亚硝酸盐等与DO具有很大的相关性,也可以运用多因子去预测DO值。
4 结论
利用EMD算法、ADPSO自适应扰动粒子群算法和LSSVM算法,构造了一个“分解-预测-重构”的组合预测模型。先将DO时间序列运用EMD进行分解,再对分解出来的各个分量进行相空间重构,构造输入输出向量,通过ADPSO算法优化LSSVM的超参数,再将优化后的LSSVM用于预测,预测出一个值再代入输入向量预测下一个时刻的值,这样通过多次迭代获得未来24 h内每个小时的DO值。相比单一的LSSVM、神经网络等其他算法,精度在一定程度上得到了提高,泛化能力得到加强。通过对养殖池塘DO预测,可及时掌握DO状况,为应对突发水质事件、水质调节、生产管理与规划提供科学的决策支撑。
□
[1] 胡金有,王靖杰,张小栓,等.水产养殖信息化关键技术研究现状与趋势[J].农业机械学报, 2015,46(7) :251-263.
[2] LIU S Y,XU L Q,LI D L, et al. Prediction of dissolved oxygen content in river crab culture based on least squares support vector regression optimized by improved particle swarm optimization[J].Computers and Electronics in Agriculture,2013,95: 82-91.
[3] HAMAAMIN Y A, NEJAD A P, EIMHEUSER M D. Application of fuzzy logic techniques in estimating the regional index flow for michigan[J]. Transactions of the Asabe, 2013, 56(1): 103-115.
[4] 张颖,高倩倩.基于灰色模型和模糊神经网络的综合水质预测模型研究[J].环境工程学报,2015,9(2):537-545.
[5] FRENI G,MANNINA G. Uncertainty estimation of a complex water quality model: the influence of Box-Cox transformation on Bayesian approaches and comparison with a non-Bayesian method[J].Physics and Chemistry of the Earth, 2012,42-44: 31 -41.
[6] 宦娟,刘星桥.基于K-means聚类和ELM神经网络的养殖水质溶氧预测[J].农业工程学报, 2016,32(17) :174-181.
[7] EMAMGHOLIZADEH S, KASHI H, MAROFPOOR I, et al. Prediction of water quality parameters of Karoon River (Iran) by artificial intelligence-based models[J].International Journal of Environmental Science and Technology,2014,11(3):645-656.
[8] 朱成云,刘星桥,李慧.工厂化水产养殖溶氧预测模型优化[J].农业机械学报,2016,47(1):273-278.
[9] 刘双印,徐龙琴,李道亮,等.基于蚁群优化最小二乘支持向量回归机的河蟹养殖溶氧预测模型[J].农业工程学报,2012,28(23):167-175.
[10] 王贺,胡志坚,张翌晖,等.基于聚类经验模态分解和最小二乘支持向量机的短期风速组合预测[J].电工技术学报,2014,29(4):237-245.
[11] HUANGA E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London A,1998,454(1971):903-995.
[12] 徐龙琴,张军,李乾川,等.基于EMD和ELM的工厂化育苗水温组合预测模型[J].农业机械学报,2016,47(4):265-271.
[13] 徐龙琴,李乾川,刘双印,等.基于集合经验模态分解和人工蜂群算法的工厂化养殖pH值预测[J].农业工程学报,2016,32(3):202-209.
[14] 高相铭,杨世凤,潘三博.基于EMD和ABC-SVM的光伏并网系统输出功率预测研究[J].电力系统保护与控制,2015,43(21):86-92.
[15] 阎威武,邵惠鹤.支持向量机和最小二乘支持向量机的比较及应用研究[J].控制与决策,2003,18(3):358-360.
[16] 田中大,高宪文,石彤.用于混沌时间序列预测的组合核函数最小二乘支持向量机[J].物理学报,2014,63(6):66-76.
[17] 温祥西,孟相如,李明迅.基于最优样本子集的在线模糊LSSVM混沌时间序列预测[J]. 应用科学学报,2013,31(4):411-417.
[18] 陈道君,龚庆武,金朝意,等.基于自适应扰动量子粒子群算法参数优化的支持向量回归机短期风电功率预测[J].电网技术,2013,37(4):974-980.
[19] 刘琦.基于LSSVM的时间序列预测方法及其应用研究[D].哈尔滨:哈尔滨工业大学,2011.
[20] 江田汉,束炯.基于LSSVM的混沌时间序列的多步预测[J].控制与决策,2006,21(1):77-80.
Prediction of dissolved oxygen based on empirical mode decomposition and least squares support vector machine
HUAN Juan1, CAO Weijian1, QIN Yilin1,2, GU Yuwan1
(1 School of Information Science and Engineering,Changzhou University,Changzhou 213164,China;2 Changzhou Technical Institute of Tourism & Commerce,Changzhou 213032, China )
The dissolved oxygen (DO) in the pond has a very close relationship with the growth of aquatic products such as fish and shrimp. In order to improve the prediction accuracy and effectiveness of DO, a combined prediction model based on empirical mode decomposition (EMD) and least squares support vector machine (LSSVM) of adaptive disturbance particle swarm optimization is proposed. First DO time series are decomposed into several components by EMD, then each component is subject to phase space reconstruction and modeling prediction by LSSVM in the phase space, and finally adaptive disturbance particle swarm optimization is applied for optimization of hyper-parameters of LSSVM and single point iterative method for multi-step prediction. The results show that the model has good prediction effect compared with single LSSVM prediction model. When DO value of next 4 h is predicted RMSE, MAPE and MAE are decreased by 13.4%, 11.3% and 1.8% respectively; when DO value of next 24 h is predicted, the three indexes are decreased by 12.9%, 12.1% and 2.7% respectively. The study shows that the combined model can extract DO series features effectively and has relatively high prediction accuracy and generalization performance.
prediction of dissolved oxygen; empirical mode decomposition; least squares support vector machine; adaptive particle swarm optimization; single point iterative method
10.3969/j.issn.1007-9580.2017.04.006
2017-06-13
国家自然科学基金项目(61640211);2016年度溧阳市第一批重点研发计划(现代农业)项目(LB2016003)
宦娟(1980—) ,女,副教授,硕士生导师,研究方向:农业信息化。E-mail: huanjuan@cczu.edu.cn
S959
A
1007-9580(2017)04-037-07
