微型飞行器的自抗扰控制器设计

高少婷，黄静雯，陈兵彬，符文星

(1.西北工业大学 航天学院，西安 710072; 2.中航工业西安飞行自动控制研究所，西安 710072)

微型飞行器的自抗扰控制器设计

高少婷1，黄静雯2，陈兵彬2，符文星1

(1.西北工业大学 航天学院，西安 710072; 2.中航工业西安飞行自动控制研究所，西安 710072)

微型飞行器具有高度的非线性特性，且气动参数具有不确定性，难以建立精确的数学模型；为实现其姿态、速度、以及高度的精确鲁棒控制，基于自抗扰控制方法设计了微型飞行器速度回路和高度回路的控制器;首先建立了微型飞行器的非线性模型，然后利用扩张状态观测器对飞行器状态和气动不确定性因素进行了估计，并通过非线性反馈对模型不确定性部分和状态耦合进行补偿，实现了纵向通道的解耦控制;通过仿真对所设计的控制器进行性能验证，结果表明自抗扰控制器能够实现对微型飞行器的快速稳定控制，且不依赖于精确的飞行器数学模型，具有良好的鲁棒性。

微型飞行器；自抗扰控制；解耦控制

0 引言

微型飞行器(MAV)体积小，在执行作战任务时隐蔽性强、机动灵活，在军事及民用方面都有很高的应用价值，因此受到越来越广泛的关注。在军事方面，微型飞行器可用于战场目标捕获、目标跟踪、损失评估等；在民用方面，微型飞行器能高效地完成环境监测、边境巡逻、及森林火灾监测等任务[1]。

微型飞行器并不是简单地针对常规武器的尺寸缩小，其具有质量轻、转动惯量小、飞行速度低、低雷诺数效应明显等特点；且微型飞行器的结构通常为特殊布局[2]，给其飞行动力学带来了明显的非线性；实际情况下微型飞行器精确的数学模型很难得到，动力学模型及气动参数会随飞行状态的改变而产生大幅度的摄动。因此为保证微型飞行器能有效地完成任务，其控制系统的设计是至关重要的。

针对微型飞行器控制系统的设计问题，主要的解决方法有自适应控制、鲁棒控制、滑模控制等。Monty J.Smith等[3]在线性状态空间模型的基础上利用线性动态逆方法设计了微型飞行器的控制器；Peter M. Thompson 等[4]将角加速度和角速度用互补滤波器结合在一起构成更为有效的速率传感器，提高系统的鲁棒性；A Jorge等[5]利用线性二次型调节器来抑制微型飞行器气动弹性带来的随机影响；但是这些方法都是在线性模型的基础上设计控制器。Xing L等[6]将遗传算法最优控制和滑模变结构控制结合在一起，抑制扰动及参数摄动带来的影响；T.J.J.Lombaerts等[7]使用H∞鲁棒控制方法设计了微型飞行器的控制系统，并与传统PID控制方法进行了对比。虽然以上方法具有良好的鲁棒性，但都是建立在模型精确已知的前提下。Matthew J S等[8]利用模型参考自适应控制方法设计了微型飞行器的姿态角控制回路，减弱了气动参数不确定带来的影响，但是模型参考自适应控制器对自适应增益较敏感，并且增益很难整定。

针对微型飞行器的高度非线性特性及气动模型不确定性，本文基于微型飞行器的非线性动力学模型，利用自抗扰控制(ADRC)方法[9-10]解决其控制问题，设计了俯仰姿态控制回路、速度控制回路以及高度控制回路的自抗扰控制器，通过MATLAB/Simulink仿真平台对控制器性能进行了仿真分析，并验证了其在气动模型发生变化时的鲁棒性。

1 微型飞行器模型

下面以纵向平面运动为例，给出微型飞行器的非线性数学运动模型。

(1)

式中，

(2)

(3)

式中，V、α、θ、y、ωz分别为飞行器的飞行速度、攻角、航迹倾角、飞行高度、以及俯仰角速率；m、Jz、S、L分别为飞行器的质量、纵向转动惯量、参考面积、参考长度；X、Y、Mz分别为飞行器在飞行中所受到的阻力、升力、俯仰力矩；ρ、Cx、Cy分别为动压头、阻力系数、升力系数。

微型飞行器的不确定性包含很多方面，主要的由气动参数不确定性以及未建模动态导致的不确定性。本文主要考虑气动参数不确定性对微型飞行器所带来的影响。气动参数不确定性主要是指气动力系数、气动力矩系数存在摄动等情况。

2 自抗扰控制器设计

对于飞行器在飞行过程中的控制，需要保证其姿态的稳定，并能快速跟踪速度及高度指令。此外，当飞行状态及环境变化时，飞行器的动力学模型会产生巨大变化，在这种情况下要保证控制系统仍能正常工作，并且具有良好的性能。

利用自抗扰控制器能够解决模型非线性和不确定性的特点，分别设计微型飞行器的姿态稳定回路、速度跟踪回路、高度跟踪回路。在设计速度跟踪回路时，因为飞行器速度主要是受推力的影响，舵偏对其的影响不大，因此可以将舵偏对其的作用当作是内部耦合来处理；同时在设计高度跟踪回路时，由于舵偏对高度影响较显著，可以看作是由升降舵偏影响飞行器的飞行高度，并将推力作为内部耦合。将速度和飞行高度变量之间的耦合看作为系统的总的干扰的一部分，扩张状态观测器可以对系统的不确定部分和干扰部分进行估计补偿，从而实现俯仰角、速度与高度之间的解耦控制，并保证系统的鲁棒性。

2.1 俯仰姿态稳定回路设计

俯仰姿态稳定回路控制即通过设计控制器保证俯仰控制姿态角的稳定。对于微型飞行器来说，在飞行过程中能够保持姿态的稳定是很重要的，在本节中给出俯仰姿态回路控制器的设计过程。

将式(1)中给出的俯仰角速率变化方程进行转化，写成便于设计自抗扰控制器的形式，经过转化，控制方程可写为：

(4)

为方便设计，记：

(5)

则式(4)最终可改写为:

(6)

令飞行器的俯仰角φ=x1，俯仰角速度ωz=x2，则可得状态方程为：

(7)

可以看出式(7)是一个典型的二阶非线性系统，其中的f是这个二阶系统的总和扰动，其中包含非线性系统模型的不确定性、干扰、以及耦合，该总和扰动可以通过扩张状态观测器(ESO)对其进行估计并实现补偿。因此设计三阶自抗扰控制器(ADRC)，其中跟踪微分器(TD)部分设计为如下形式：

(8)

在上式中，fhan(·)为非线性函数，v0是系统的期望输入信号，v1是v0的跟踪值，v2是v0的近似微分值，r0,h是需要确定的控制参数。通过调整r0可以控制过渡过程的快慢，r0值越大，v1能v0越快地跟踪v0，但会受到系统承受能力的约束；h为步长，同时当输入存在噪声时，可以起到一定的滤波效果。跟踪微分器(TD)具有良好的跟踪特性，能够快速跟踪输入信号且没有超调，在此基础上还能够给出相应的微分信号，合理地安排了过渡过程，实现了对输入信号及其微分的跟踪。

扩张状态观测器(ESO)的实质是通过对高阶的微分信号求积分来求得低阶的微分信号，估计出系统的状态变量x1,x2以及系统的总和扰动f(x,x(1),…,x(n-1),t)，利用跟踪微分器求得的输入信号跟踪值与扩张状态观测器的状态变量估计值作减法运算求得误差，再通过非线性反馈组合得到控制量。

设计的ESO具体表达式为：

(9)

误差反馈采用非线性函数，具体形式如式(10)所示：

(10)

如式(10)所示，最终的控制量是由非线性函数计算得到的控制量减去扩张状态观测器估计出的总和扰动而得到，通过非线性反馈对总和扰动进行补偿，使得控制系统变为一个单纯的积分环节。

俯仰姿态稳定回路的ADRC控制框图如图1所示。

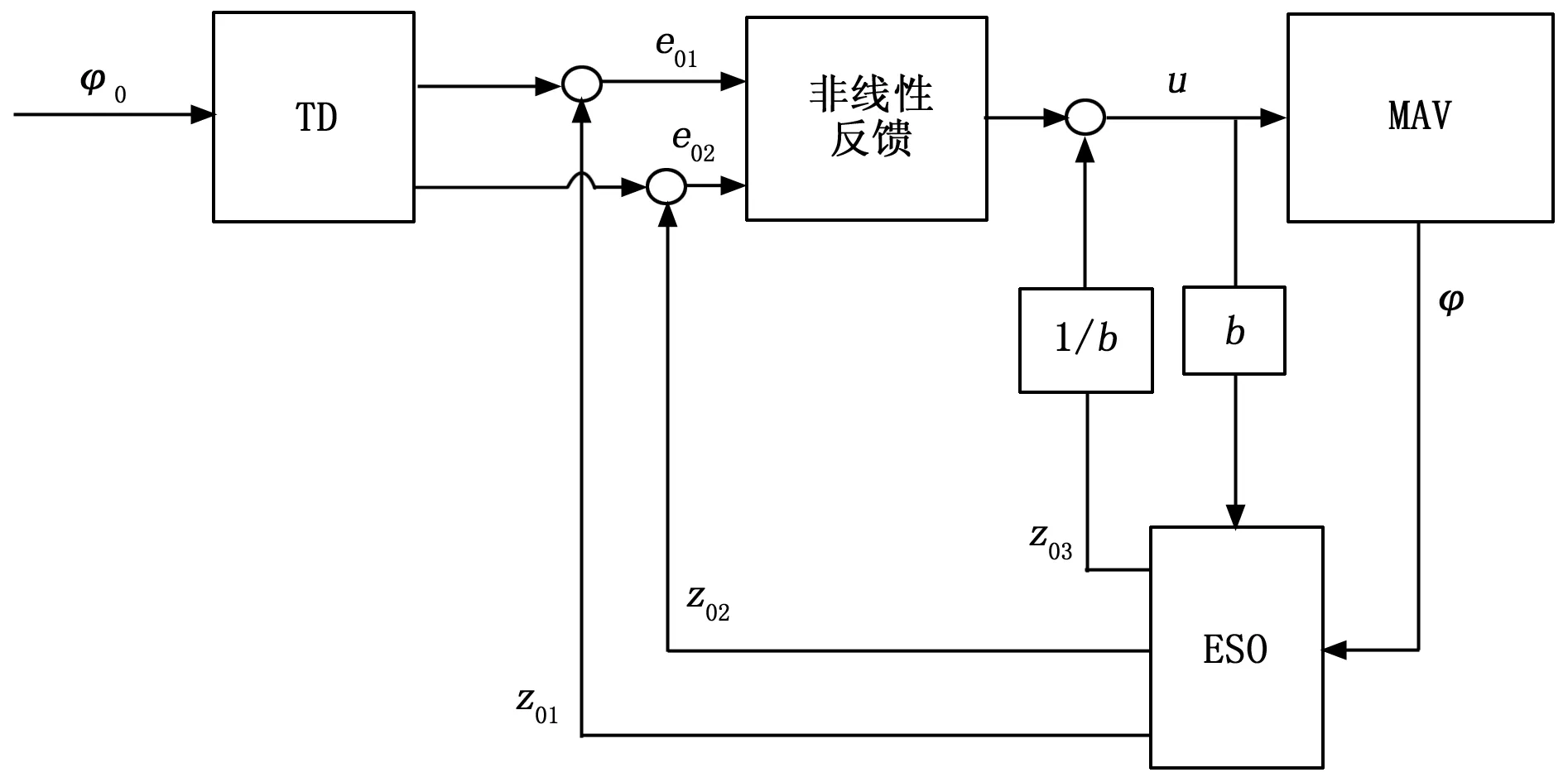
图1 俯仰姿态稳定回路的控制框图

2.2 速度跟踪回路设计

速度回路控制器的目的是使微型飞行器能够快速、稳定地跟踪输入的速度指令。速度变化方程也可转化为类似式(6)的形式为：

(11)

可以看出，式(11)是一个一阶微分方程，所以针对速度回路设计相应的二阶ADRC。跟踪微分器TD1与俯仰角稳定回路形式类似；扩张状态观测器ESO1设计为二阶形式：

(12)

误差反馈控制律采用非线性函数为：

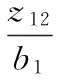
(13)

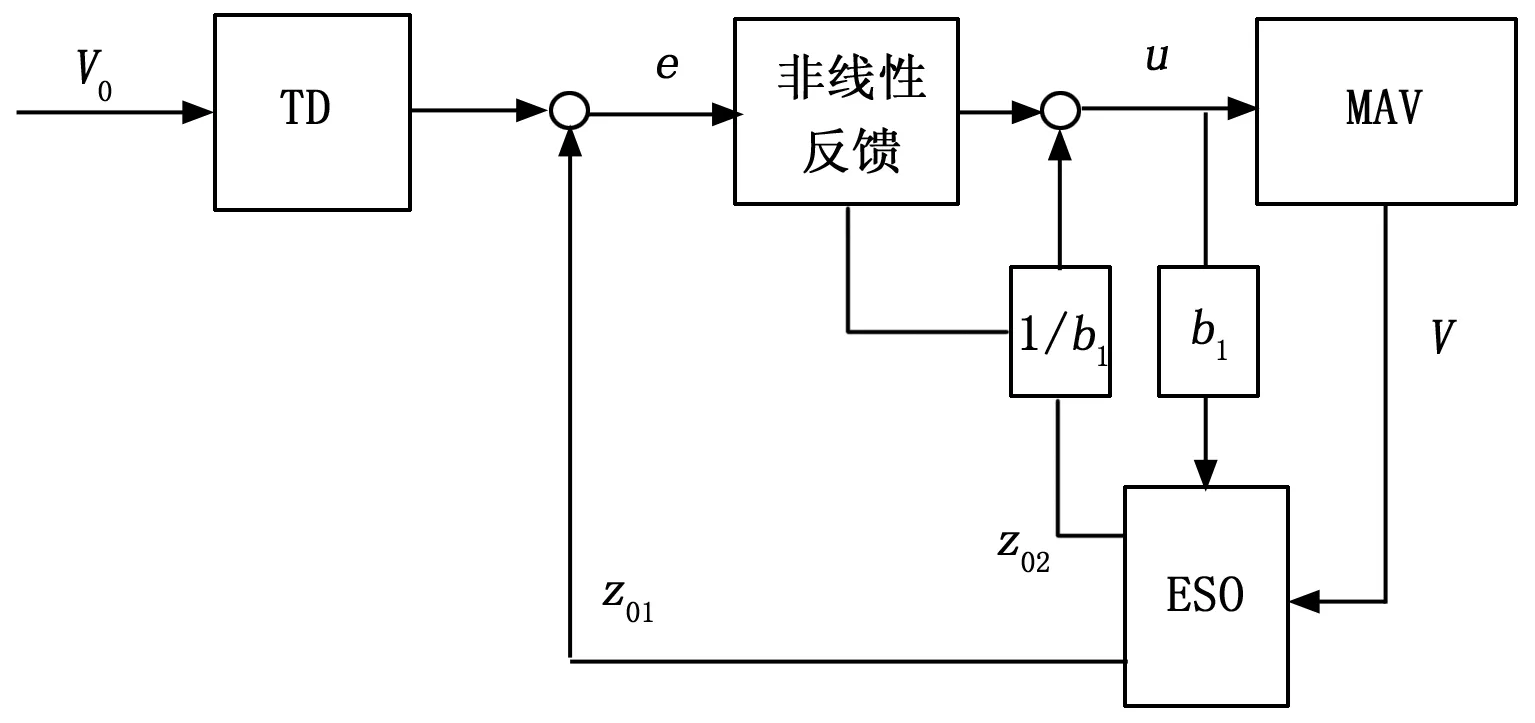
图2 速度跟踪回路的控制框图

2.3 高度跟踪回路设计

实现飞行器速度和高度之间的解耦控制，只考虑舵面偏转对高度变化的影响，将其看作是一个单输入单输出问题。因为对于控制高度变量来说，不能直接将其表达式表示成关于俯仰舵偏角的一阶微分方程或二阶微分方程，所以需要建立内外环控制。内环系统的输出反馈为航迹倾角，而外环输入期望高度指令y0，飞行器实际高度作为输出反馈，通过外环控制器得到期望的航迹倾角θ0，作为内环输入指令进一步得到控制输出即俯仰舵偏角δe，从而实现高度的快速跟踪。内外回路单独设计控制器ADRC，将子回路间的耦合加入到总和干扰中，通过扩张状态观测器对干扰进行估计补偿，从而实现解耦控制。

航迹倾角与俯仰角之间的关系式为：

θ=φ-α

(14)

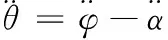
(15)

将式(1)代入到式(15)中，令:

(16)

(17)

所以可得式：

(18)

期望的航迹倾角θ0与实际输出的航迹倾角θ之间的传递函数可表示为一阶惯性环节：

(19)

故高度关系式可改写为：

(20)

简化为：

(21)

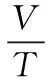
内外回路皆为二阶系统，故内回路ADRC2与外回路ADRC1与俯仰角稳定回路扩张状态观测器类似。

高度跟踪回路的双闭环控制框图如图3所示。

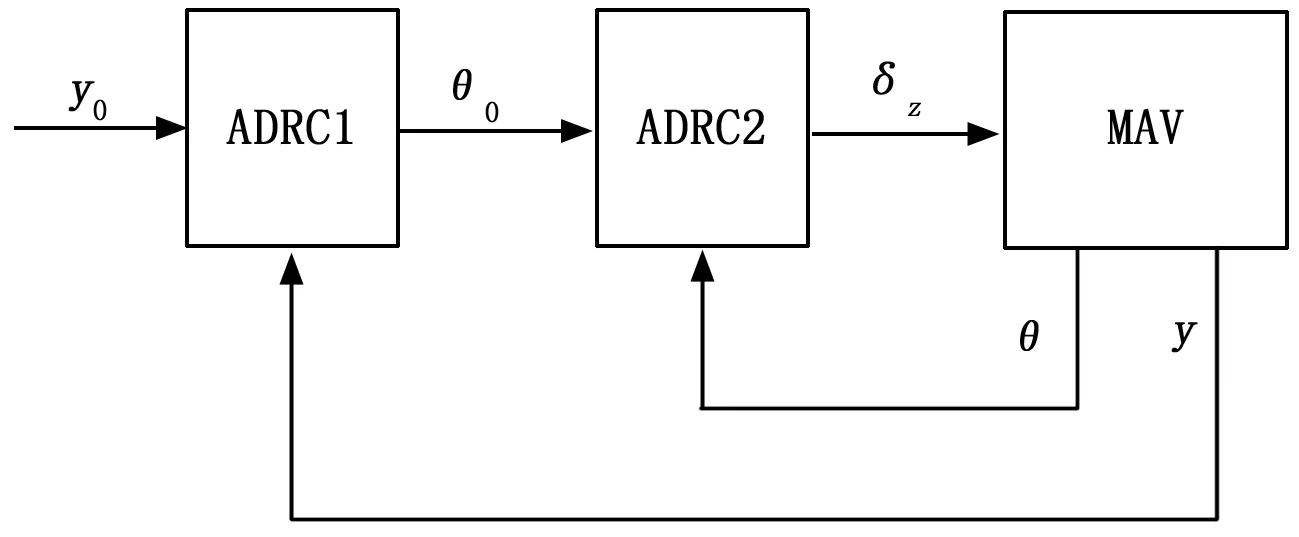
图3 高度跟踪回路的双闭环控制框图

3 仿真试验与结果分析

以某型微型飞行器为研究对象，建立其运动方程数学模型，设计控制器，并在此基础上调节控制器参数，利用MATLAB验证设计的自抗扰控制器的性能，要求飞行器作无侧滑且无倾斜的运动。初始状态为：俯仰角φ=10°，速度V=10 m/s，高度H=500 m。对控制器进行参数整定，俯仰角稳定回路控制参数：r0=4，h=0.01，δ=0.5，β01=18，β02=800，β03=1 000；速度回路控制参数为：r0=20，h=0.01，β11=500，β12=1 300；高度回路控制参数为：r0=20，h=0.01，外回路ESO控制参数：β01=10，β02=120，β03=300，内回路ESO控制参数：β01=500，β02=5 400，β03=12 000；控制目标为将俯仰角镇定至0°；速度指令为30 m/s；高度指令为1 000 m。

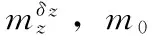
1)俯仰角响应曲线及误差曲线；

2)速度跟踪曲线及跟踪误差曲线；

3)高度跟踪曲线及跟踪误差曲线。

仿真结果显示，图4中俯仰角初始值在10°，经过1 s左右，系统输出进入稳定状态，达到0°，相应快速，没有超调，满足微型飞行器短周期运动的要求；在气动参数存在摄动时，仍能够快速的实现对姿态角的稳定，控制器能达到使俯仰角稳定的要求。

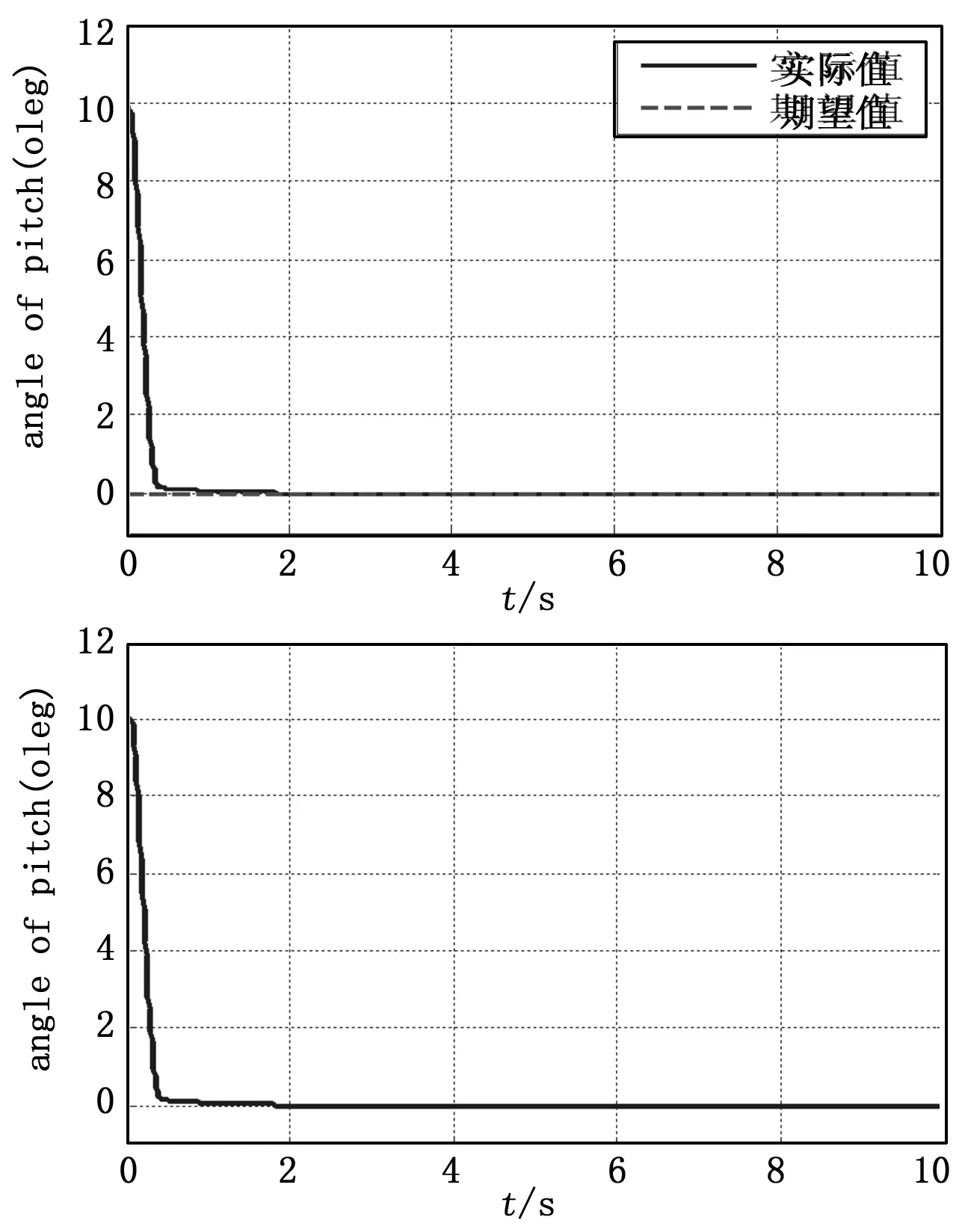
图4 干扰下俯仰角镇定实验结果

在图5、图6中，输入指令分别为：速度在10 s内由10 m/s上升至30 m/s的曲线，高度在20 s内由500 m上升至550 m的曲线，分析图中实际飞行情况，可知速度及高度皆能快速跟踪上指令信号，响应曲线平滑，时间延迟最大为0.5 s，且稳态误差小于0.1%，并且速度和高度能够互不干扰地跟踪各自的指令信号，实现了速度与高度之间的解耦控制。并且当速度、高度大范围变化，控制器参数不变，仍能达到控制要求，并具有良好的动态性能。

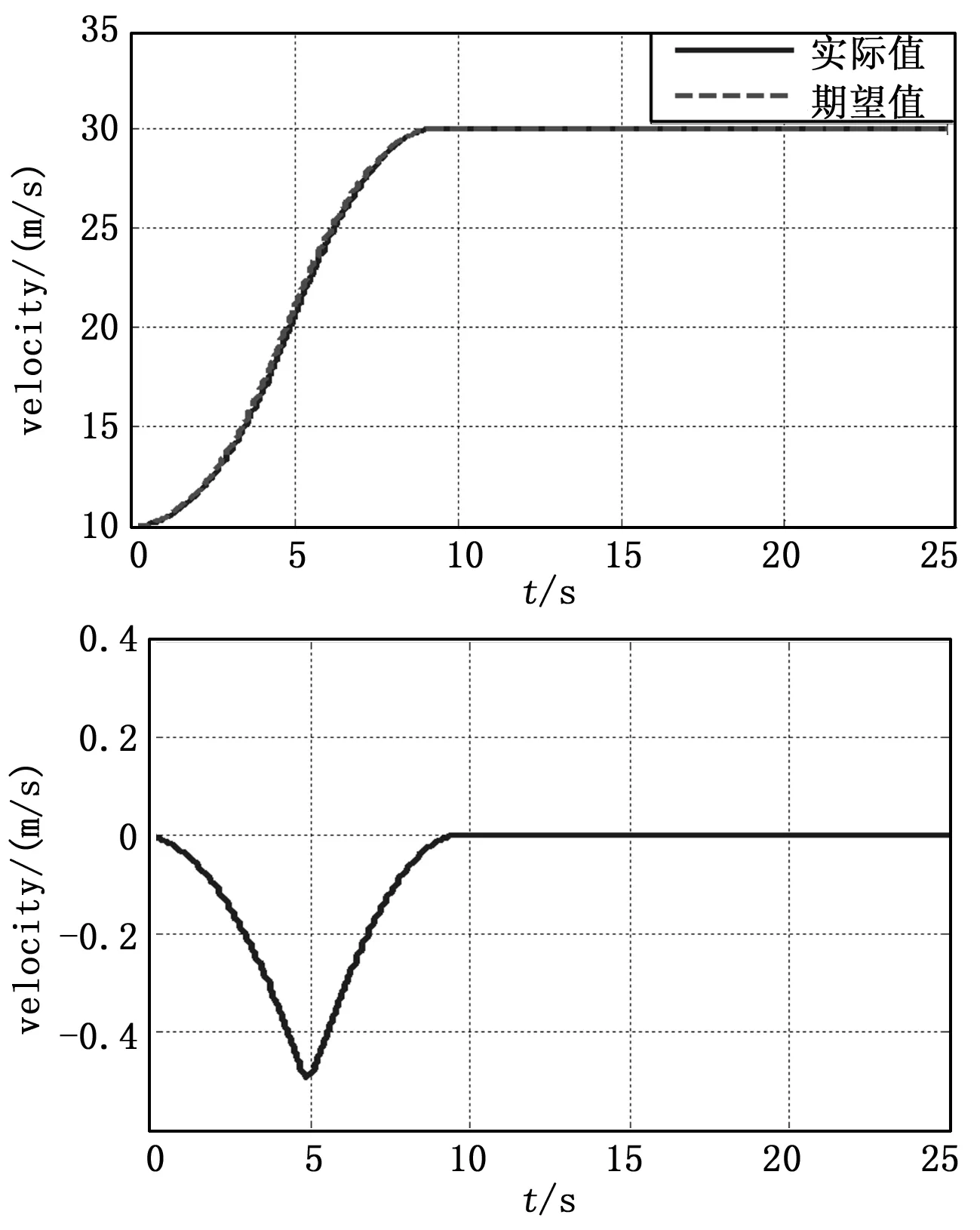
图5 干扰下速度跟踪实验结果

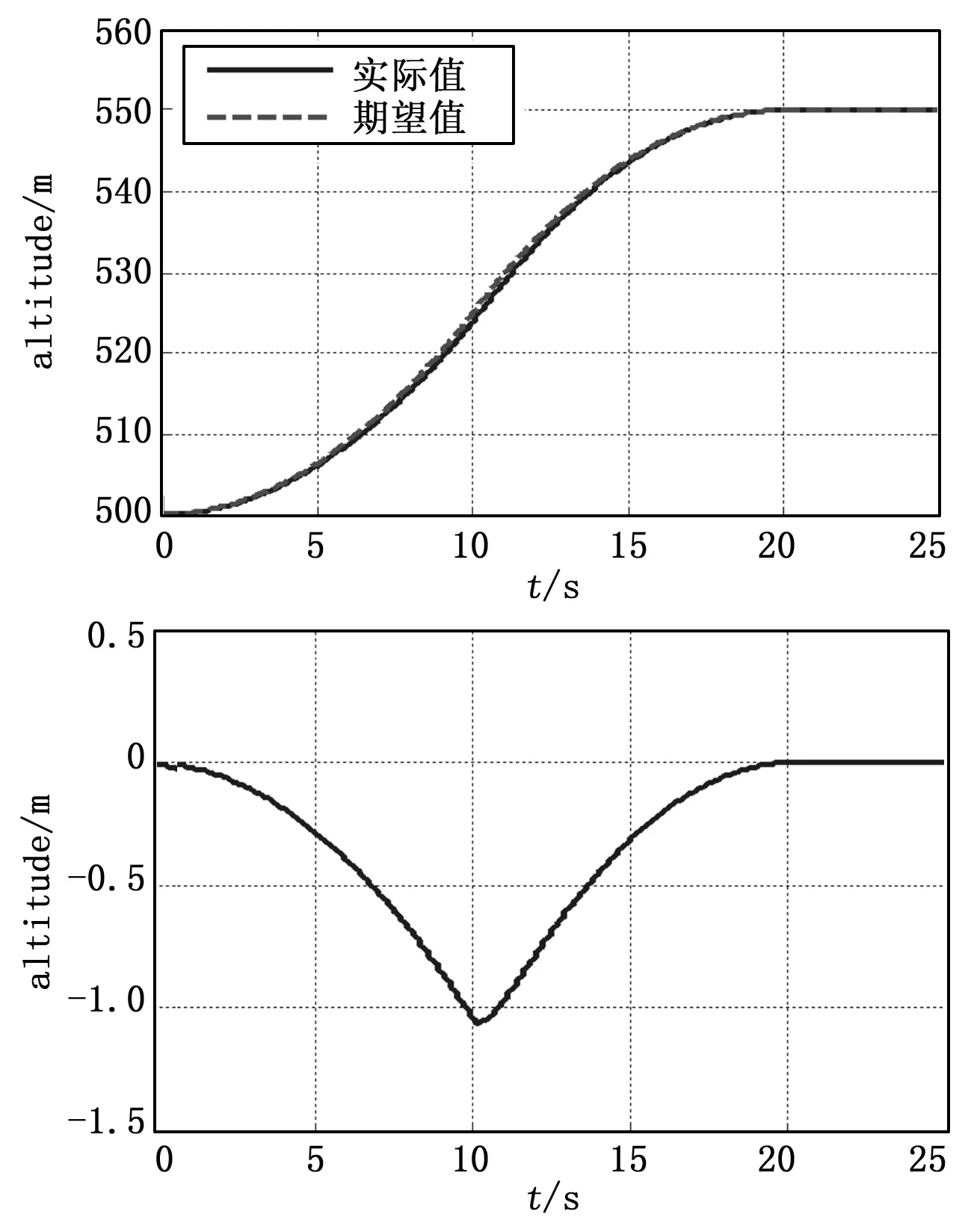
图6 干扰下高度跟踪实验结果

仿真结果显示，在引入模型参数摄动后，系统仍能达到指令值后稳定在平衡位置，表明自抗扰控制器很好地补偿了参数的不确定性影响，具有很强的鲁棒性。

4 结论

本文基于自抗扰控制技术设计了微型飞行器的控制器，提供了一种微型飞行器控制器的设计方法。微型飞行器由于低雷诺数、易受干扰等原因，使得其气动参数不确定、气动模型具有很高的非线性，给使微型飞行器控制系统的设计带来了难题。自抗扰控制方法可以直接针对飞行器非线性模型设计控制器，且能很好的补偿系统的不确定性及外部干扰，在很大的飞行状态包线内不需要改变控制器的设计参数，就能很好的达到控制的目的，动态性能好，且具有很强的鲁棒性，可以在工程上广泛应用。

[1] 昂海松.微型飞行器的现状、难题和发展趋势[A]. 2014(第五届)中国无人机大会论文集[C].2014:653-658.

[2] Reed H L, Saric W S. Aerodynamic Studies of Micro Air Vehicles[M]. 2001.

[3] Smith Monty, Swei Sean, Tischler Mark. A Study of the Control of Micro Air Vehicles Using the Linear Dynamic Inverse Approach[A]. AIAA 1st Intelligent Systems Technical Conference[C]. 2004, American Institute of Aeronautics and Astronautics.

[4] Thompson Peter M, Lampton Amanda K, Lind Richard C, et al. Attitude Control Enhancement for Small and Micro Air Vehicles Using Acceleration Feedback[A]. AIAA Atmospheric Flight Mechanics (AFM) Conference[C]. 2013, American Institute of Aeronautics and Astronautics.

[5] Jorge Ahmed, C. Lind Richard. Control of a Stochastic Model of an Aeroelastic Micro Air Vehicle in Turbulence[A]. AIAA Atmospheric Flight Mechanics (AFM) Conference[C]. 2013, American Institute of Aeronautics and Astronautics.

[6] Xing L, Yu X. Sliding Mode Variable Structure Optimized Control For Micro-Air-Vehicle Attitude Control Systems[A]. Mechatronic Science, Electric Engineering and Computer (MEC)[C]. 2011 International Conference on, 2011:460-463.

[7] Lombaerts T J J, Mulder J A, Voorsluijs G M, Design of a Robust Flight Control System for a Mini-UAV[R]. AIAA, 2005:6408.

[8] Matthew J S, Knoebel N B, Osborne S R, et al. Adaptive backstepping control for miniature air vehicles[A]. 2006 American Control Conference[C]. Minnesota, USA, 2006.

[9] 栗金平，杨 军. 基于自抗扰技术的高超声速飞行器控制系统设计[J]. 计算机测量与控制，2011, 19(5):1055-1057.

[10] 胡海燕，徐 敏. 无人机飞行控制系统的自抗扰姿态稳定控制[J]. 遥测遥控，2012, 33(3):62-67.

Active Disturbance Rejection Control for Micro Aerial Vehicle

Gao Shaoting1，Huang Jingwen2，Chen Bingbin2，Fu Wenxing1

(1.College of Astronautics，Northwestern Polytechnical University, Xi’an 710072, China;2.AVIC Xi’an Flight Automatic Control Research Institute, Xi’an 710072,China)

The micro aerial vehicle's (MAV) dynamic is nonlinear; in addition, due to the uncertainty aerodynamic parameters of MAV, it is difficult to establish the accurate mathematical model. So, controllers of altitude and velocity tracking is designed with the active disturbance rejection control (ADRC) algorithm aiming to achieve the high quality control of MAV’attitude, velocity, and altitude. In the first place, the nonlinear model of the MAV is established. Then, the vehicle’s state and uncertainty factors is estimated by the extended state observer; the uncertainty parts and state coupling is compensated with the nonlinear feedback. Thus, the decoupling control of longitudinal channel was implemented. Finally, there is a simulation in order to demonstrate the performance of the designed controller , the result shows that the proposed ADRC control law can improve the robust performance of the system, and the effects is independent of the accurate mathematical model.

micro aerial vehicle；active disturbance rejection control；decoupling control

2016-12-20；

2017-02-06。

国家自然科学基金(U1630127)。

高少婷(1992-)，女，陕西西安人，硕士研究生，主要从事导航制导与控制方向的研究。

1671-4598(2017)07-0136-04

10.16526/j.cnki.11-4762/tp.2017.07.034

V249.1

A