一种改进人工蜂群的分数阶PID控制器优化算法
2017-08-30胡海涛陈超波
胡海涛,高 嵩,陈超波,曹 凯
(西安工业大学 电子信息工程学院,西安 710021)
一种改进人工蜂群的分数阶PID控制器优化算法
胡海涛,高 嵩,陈超波,曹 凯
(西安工业大学 电子信息工程学院,西安 710021)
针对分数阶PID控制器参数整定过程参数多复杂性大,传统靠经验试凑的方法不易实现且优化效果差的问题,提出了一种改进的人工蜂群算法,实现分数阶PID控制器参数的整定;该算法通过改进人工蜂群算法中搜索方程,并引入一个淘汰机制,对分数阶控制器参数进行群智能搜索,将搜索到的参数送至分数阶PID控制器中反复迭代,以带有权值的误差绝对值积分指标(AIE)作为人工蜂群寻优的目标函数,最后得出控制器;本文以非线性系统为被控对象,经过实例仿真,验证了该算法实现的控制器比传统整数阶控制器和未改进的人工蜂群算法实现的分数阶控制器的动态性能和稳态性能都有所提高,在超调、上升时间、振荡性方面都优于未改进算法。
人工蜂群算法;分数阶;控制;最优化
0 引言
分数阶系统比整数阶可以更精确的描述很多自然现象和现实过程,分数阶控制器的控制效果也比整数阶更具柔性,控制范围也从整数阶点状网格扩展到面状[1]。凭借在机械化工、自动化控制领域等有着整数阶不可比拟的性能,近年来被广泛应用在PID控制器中。文献[2]提出的分数阶PID控制器设计方法,证明了分数阶控制器在动态性能等方面效果比整数阶好。文献[3]研究了分数阶非线性系统控制具有稳定性。然而分数阶系统的数字实现一直是一个难点,根据分数阶定义公式直接计算非常困难,因而出现了多种多样的近似方法,有直接近似法、连分式近似法、Carlson近似法等多种常用的似方法中,在这些方法中改进Oustaloup近似方法效果较好且易于数字实现,故得到广泛的应用。文献[4]给出了一种Oustaloup近似方法的数学分析和数字实现推导过程。文献[5]给出了分数阶系统和分数阶PID控制器数值求解过程和MATLAB实现方法。虽然这些方法可以实现分数阶PID控制器,通过多引入了λ和μ两个参数,使控制器参数整定范围变大,控制效果也更好,但分数阶PID更多的参数使得控制器参数的整定和设计比整数阶更复杂,传统的试凑法和靠经验整定参数变得更加困难。
很多学者和研究人员开始将智能控制引入分数阶PID控制器的参数整定中,如遗传算法、粒子群、蚁群等群智能算法都被相继应用到分数阶系统。文献[6]提出了一种基于改进粒子群算法的分数阶系统辨识方法。文献[7]提出了一种基于遗传算法的分数阶控制器分级整定方法。这些群智能算法加速了分数阶的应用和开发。智能算法中人工蜂群算法作为一种新的算法,自2008年传入国内就得到了广泛关注[8]。它是一种基于模拟蜂群采蜜行为而提出的群智能搜索优化算法,几乎能够很好地处理所有计算机科学、管理科学和控制学科等领域的全局优化问题,且其控制参数少,易于实现,其中文献[9]和[10]都对人工蜂群做了不同研究,文献[9]在蜂群迭代过程中引入了OBL策略,提高了收敛速度,文献[10]提出了一种改进的人工蜂群算法并将其应用到整数阶参数整定中。
本文在以往人工蜂群算法的基础上,通过引入一个概率调节机制和一个淘汰机制分别对其搜索方程和蜜源更新概率进行改进。改进后的人工蜂群算法结合改进的Oustaluop近似方法进行数字实现,最后以一个非线性系统进行仿真分析,证明了改进后的算法全局搜索能力和搜索速度都有所提高。改进后的算法实现的控制器在阶跃响应下超调、上升时间、振荡性等都变小,精度更高,正弦跟踪曲线也更理想。
1 分数阶PID
1.1 分数阶微积分定义
分数阶微积分中其积分,微分的阶次是任意的,故整数阶可以看成是特殊一部分,分数阶可以看成是整数阶的扩展。经常用到的分数阶定义有Grunwald-Letnikov定义和Riemann-Liouville定义。
若函数f可导,其m阶微积分Grunwald-Letnikov定义如下:
(1)
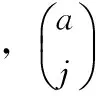
Riemann-Liouville分数阶微积分定义中,积分定义:
(2)
微分定义:
(3)
1.2 改进的Oustaloup近似方法
虽然1.1中公式可以较为精确的计算出给定信号的分数阶微积分,但在实际应用中不易实现具有很大的局限性。故出现了很多近似方法,其中Oustaloup效果较好。Oustaloup近似方法主要基于对(4)式的近似上。
H(s)=(s/ωμ)a,a∈R+
(4)
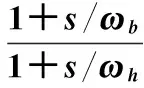
(5)
式中,0
(6)
式中,-N为第k个零点,N为第k个极点。
改进后的Oustaloup近似方法在整个近似频段内都能达到一定要求而且一定程度上提高了近似的准确度。
1.3 分数阶PID控制器
目前的分数阶控制器主要有:分数阶PID控制器,TID控制器,CRONE控制器和超前滞后矫正补偿器等4种,应用最广泛的是Podlubny提出的分数阶PID控制器,与整数阶相比它引入了两个可变参数,使其控制范围更广,无论在目标跟踪还是扰动特性、鲁棒性方面的控制性能更加优良。其传递函数表达式为:
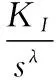
(7)
故构成分数阶控制器模型如图1。
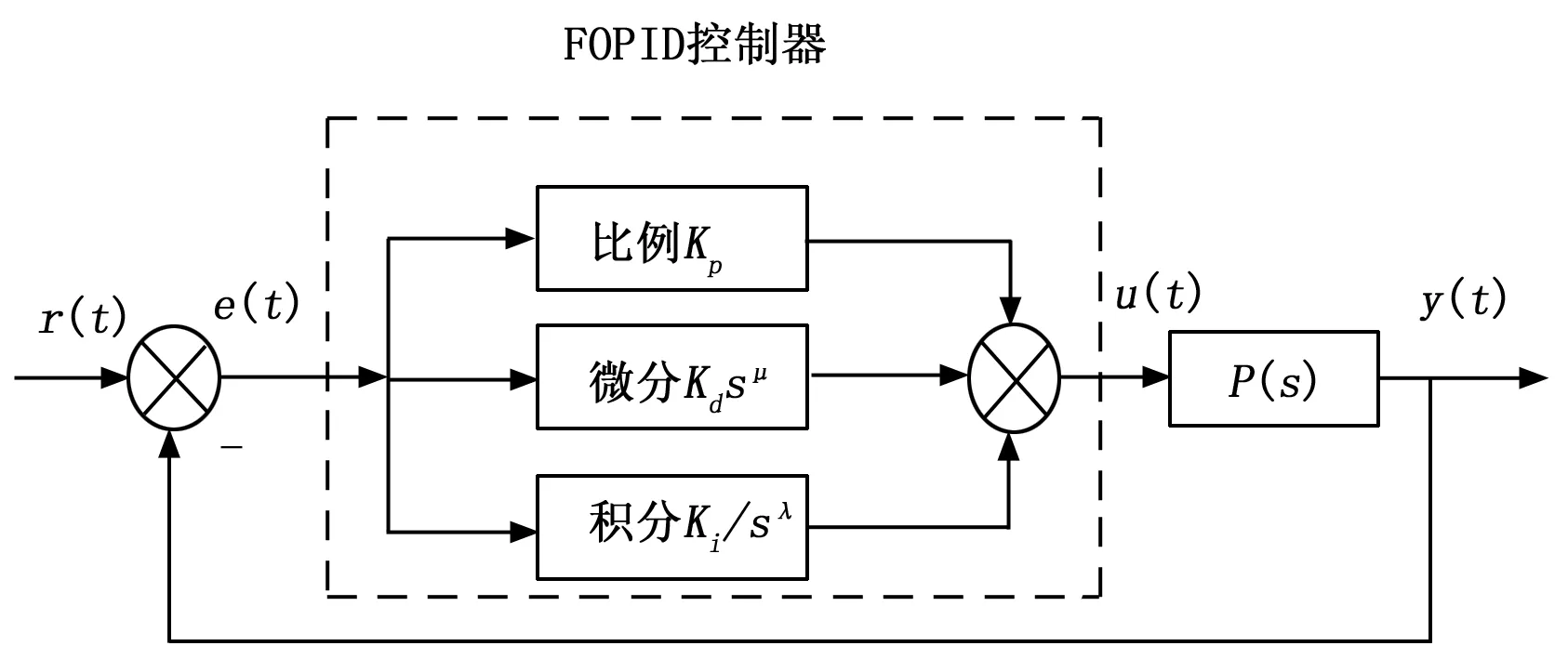
图1 分数阶控制器模型
2 人工蜂群算法及改进
2.1 人工蜂群算法
人工蜂群算法将不同行为蜜蜂分为三类:采蜜蜂、观察蜂、侦查蜂,其中采蜜蜂和观察蜂数量相同且等于蜜源数量,可认为其各占整个蜂群数量的一半;采蜜蜂负责寻找蜜源并记忆信息与观察蜂分享蜜源信息,观察蜂在舞蹈区等待选择要采蜜的蜜源,放弃原先蜜源的采蜜蜂转变为侦查蜂随机寻找新蜜源。
蜜蜂在选择蜜源过程中根据一概率值:
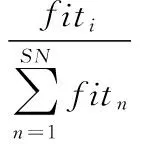
(8)
选择蜜源。其中fiti是解Xi的适应度值;xi(i=1,2,…,SN)是一个D维向量,D为优化参数个数;SN为种群中解的个数。在每次选择中无论适应度值结果如何,都以相同权值计入,那些结果很差的值对挑选好的蜜源产生着很大影响。
蜜蜂根据原蜜源产生新候选密源的迭代公式:
vij=xij+φij(xij-xkj)
(9)
其中:k为不同于i的蜜源,j为随机选择的下标,φij为[-1,1]之间的随机数。这样φij无论在搜索前期还是后期都随机的产生一个随机数,这种以轮盘赌选择法来选择蜜源前期容易陷入局部解、后期容易过早收敛,而且搜索精度只能控制在一定范围。
2.2 较差结果淘汰机制
本文根据适应度函数的结果对较差值的权值进行修改,结果值越差权值越小,这样就可以对结果进行筛选,蜜源选择概率修改如下:
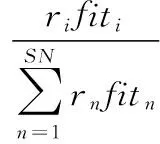
(10)
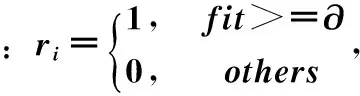
2.3 搜索方程改进
本文针对原来人工蜂群中以轮盘赌选择法以随机概率选择蜜源容易出现陷入局部解、过早收敛等问题提出了一种概率机制,通过改进随机选择机制,改进搜索方程。
以上次迭代最优蜜源为中心,以随机数选择一个新地点,同时对随机数进行约束。将新选择地点与原蜜源差值以随机权值在原蜜源上叠加得到新蜜源。表达式如下:
vij=xbest,j+φi,j(xbest,j-xk,j)
(11)

3 改进人工蜂群算法的PIλDμ控制器
3.1 算法设计原理
首先初始一个蜂群,设置参数范围和最大循环次数等值防止陷入死区。然后将蜂群进行迭代,将本次迭代的最优结果带入分数阶PID控制器中,以带有权值的AIE(Integral of absolute error)指标作为改进人工蜂群算法目标函数和适应度值,并对新产生的值做贪婪选择,进入下一轮迭代,产生新解,直至循环结束。
本文中以带有权值的误差绝对值积分指标AIE作为改进人工蜂群算法目标函数,表达式如下:

(12)
式(12)中在目标函数中加入控制输入的平方项目的是为了防止控制能量过大。e(t)为系统误差,u(t)为控制器输出,tu为上升时间,w1,w2,w4,w3为权值。为了避免超调,采用了罚函数功能,如果e(t)<0,目标函数变为:

(13)
3.2 控制器算法迭代步骤
1)设定PIλDμ各参数(kp,ki,kd,λ,μ)范围,蜂群大小,目标函数,并随机产生初始蜂群,计算各解适应度,记录最优解;
2)设置循环次数;
3)采蜜蜂根据式(11)邻域搜索;产生新的PIλDμ各参数值;
4)观察蜂根据式(10)选择食物源,并根据式(11)搜索产生新解;
5)将新得到的参数带入PIλDμ控制器,并运行系统得到输出,根据输出,及误差计算适应度值;
6)对要放弃解,根据侦查蜂搜索公式产生新解替换原解;
7)记录最优解;
8)循环次数加1,如果未到达设定最大值,转至3)。
4 仿真结果与分析
为了验证本文改进算法的优越性,以一个复杂的非线性系统进行PID控制器参数整定,并绘出单位阶跃和正弦响应曲线。蜂群算法中取最大迭代循环次数N=500,蜂群大小NP=20,选择被控对象如下:

(14)
将其用带延迟的降阶模型逼近有:
Gr(s)=0.1836e-0.827s/(s+0.18326)
(15)
取采样时间为1s,输入信号为单位阶跃,本文目标函数中选Kp范围为[0,20],Ki,Kd,范围为[0,1],取w1=0.999,w2=0.001,w3=2.0,w4=100。分别用改进后的蜂群算法实现的分数阶控制器和未改进算法实现的控制器对其进行作用,对输出结果呢进行比较。
系统在单位阶跃输入下,仿真结果如图2所示。
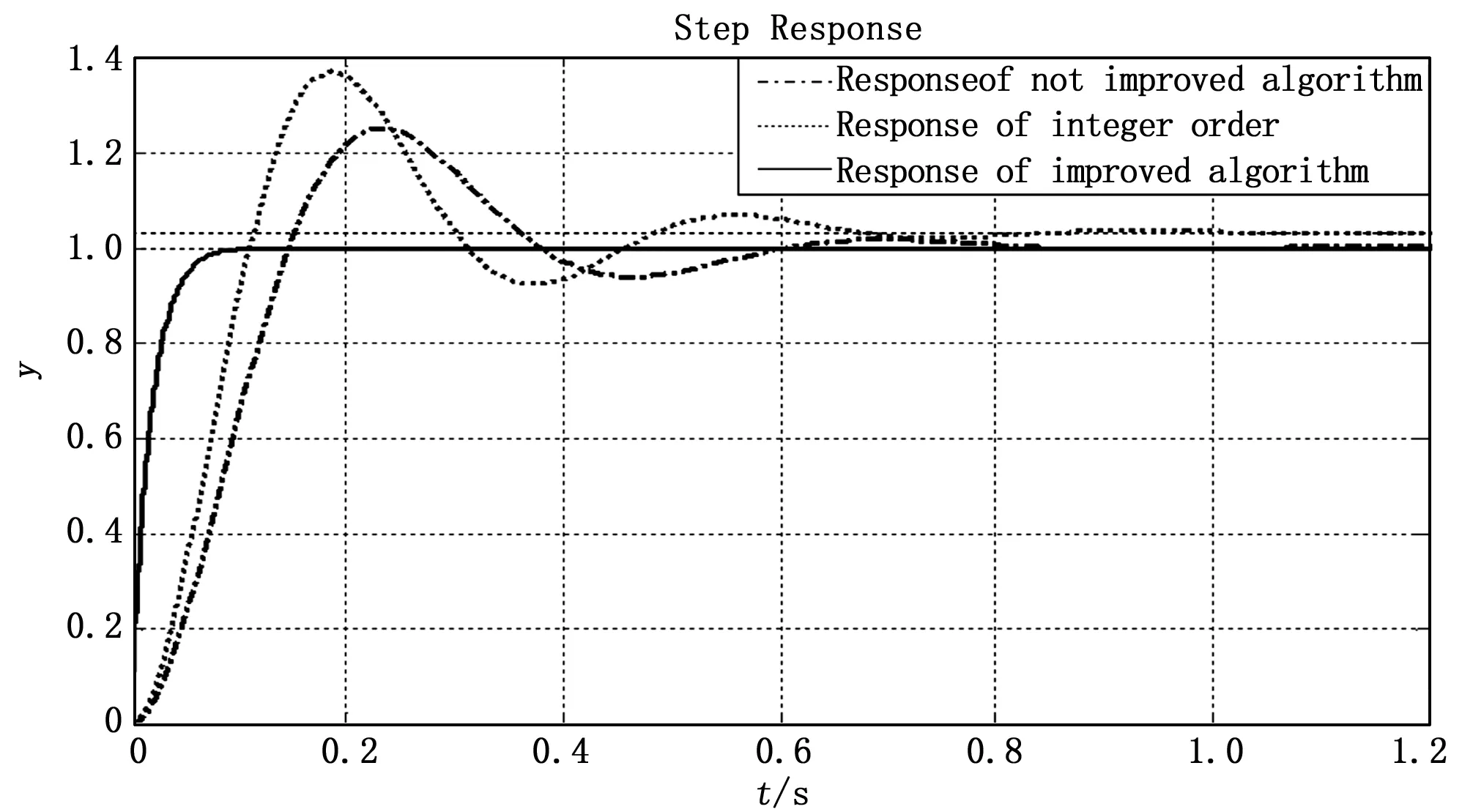
图2 改进前后控制效果对比图
从图2中可以看出改进后的人工蜂群算法整定的控制器在阶跃信号下响应曲线比未改进算法的控制曲线超调更小,振荡性更小,而且更快的趋于稳定。相比于整数阶控制器的器控制效果,超调量和稳定时间也都更小,精度更高。

表1 系统分别在不同算法下参数整定值
kp,ki,kd,λ,μ——分数阶控制器各参数,td——迭代时间,GlobalMin——最优目标值
从表1中可以看出,分数阶控制器目标值(误差)小于整数阶;改进后算法实现的控制器的目标值小于未改进算法实现的控制器,而且迭代时间更短。
图3给出了改进算法代价函数值J的优化过程在正弦信号输入下,改进后算法实现的控制器和未改进的系统位置跟踪仿真结果如下:

图3 改进算法代价函数值优化过程
图4和图5为初始值取0.5的偏差时的正弦响应结果。从图中可以看出,改进前正弦跟踪误差曲线在起初有大的偏离外,一直都存在波动误差。改进后算法跟踪误差则逐渐趋于零。故改进后算法正弦响应下的的位置跟踪结果比未改进的结果更优良。
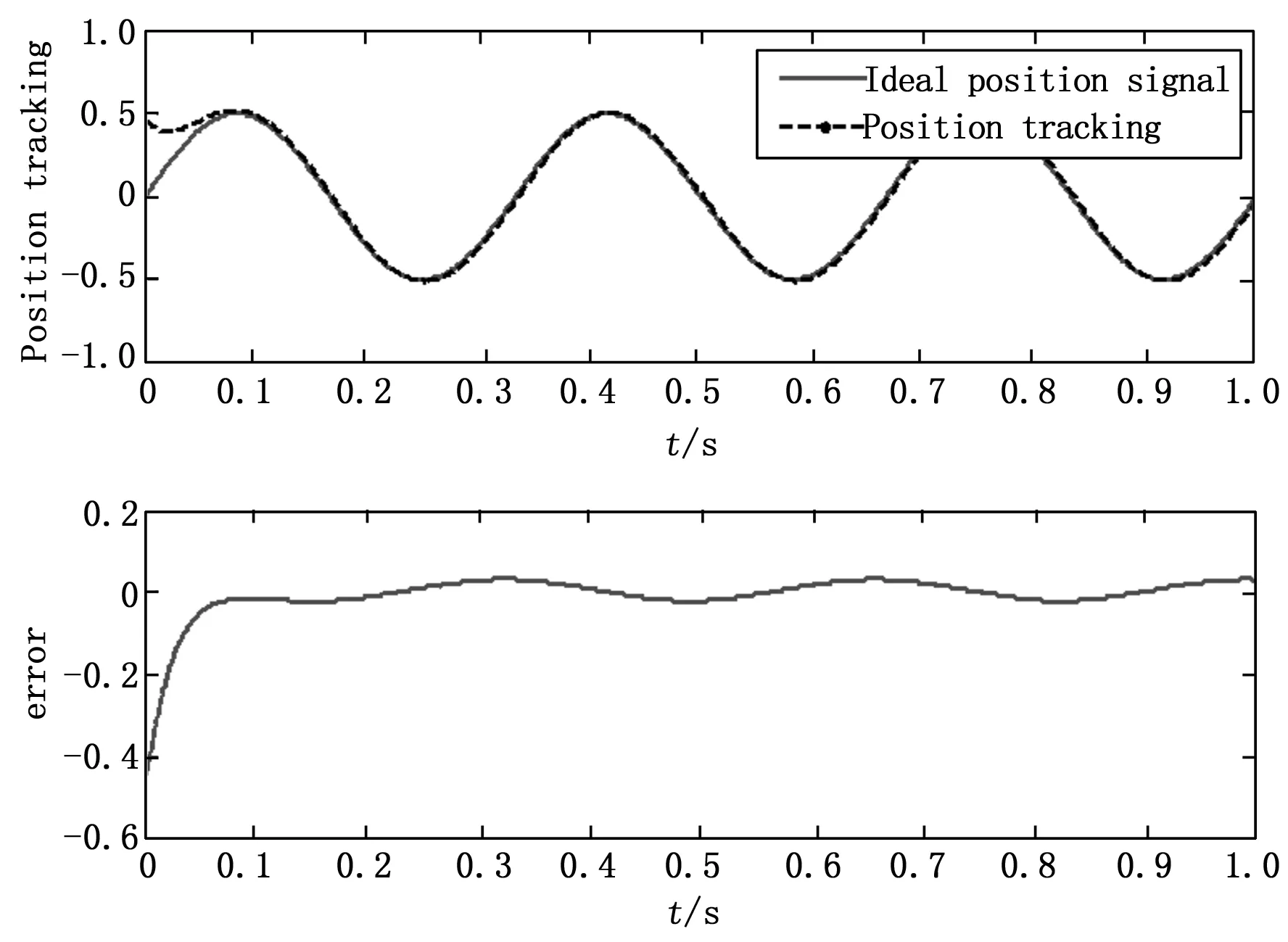
图4 未改进算法的正弦响应跟踪曲线及误差曲线

图5 改进后算法的正弦响应跟踪曲线及误差曲线
图6、图7为初始值无偏差时正弦响应结果。可以看出即使在无偏差跟踪中,未改进算法的正弦跟踪误差跟改进后算法相比还是一直存在。
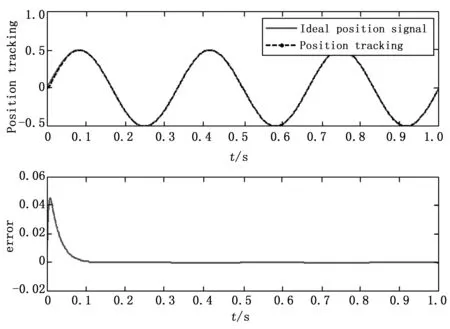
图6 改进后算法的正弦响应跟踪曲线及误差曲线

图7 未改进算法的正弦响应跟踪曲线及误差曲线
5 结束语
分数阶控制器参数多,设计更灵活,整定也更加困难。本文提出的改进的人工蜂群算法,通过引入优胜劣汰机制和对搜索方程的改进,来提高对参数搜索的效率和精度。最后结合改进的Oustaluop近似方法,数字实现了该控制过程。通过MATLAB仿真实验,分别以改进前和改进后算法实现的控制器以及整数阶控制器在阶跃响应输出,以及误差曲线分析,证明了改进后的算法实现的控制器在阶跃响应下的超调、稳定时间、振荡性方面都要优于未改进的算法;在正弦响应下改进的算法的跟踪误差也基本趋进于零。从另一方面证明改进后的算法全局搜索能力,搜索精度都有所提高。
[1] 赵春娜,李英顺,陆 涛.分数阶系统与设计[M].北京:国防工业出版社,2010.
[2] 薛定宇,赵春娜.分数阶系统的分数阶控制器PID控制器设计[J].控制理论与应用,2007,25(5):771-776.
[3] 胡建兵,赵灵东.分数阶系统稳定性理论与控制研究[J].物理学报,2013,62(24):1-7.
[4] Alain Oustaloup, Francois Levron, Benoit Mathieu M.Nanot etc. Frequency-Band Complex Noninteger Differentiatior: Characterization and Synthesis[J].Fundmental Theory and Applications,2000,7(1):25-39.
[5] Xue Dingyu.Computer Aided Control Systems Design.Using MATLAB Language[M].北京:清华大学出版社,2012.
[6] 王 强,赵志成,桑 博.基于改进粒子群算法的分数阶系统辨识方法[J].太原科技大学学报,2014,35(3):203-206.
[7] 李 文,刘 洋.基于遗传算法的分数阶控制器参数分级整定[J].大连交通大学学报,2009,30(6):83-85.
[8] 余胜威.MATLAB优化算法案例分析与应用(进阶篇)[M].北京:清华大学出版社,2015.
[9] 毕晓君,万艳娇.改进人工蜂群算法[J].哈尔滨工程大学学报,2012,33(1):118-123.
[10] 李荣雨,朱正方.改进人工蜂群算法在MFAC参数整定中的研究[J].自动化仪表,2016,37(8):75-79.
[11] 陈超波,胡 莉,马 颖,等.一种改进式遗传算法优化分数阶PID控制器[J].西安工业大学学报,2016,36(6):511-516.
[12] Li M D, Xiong W, Liang Q.Wireless Sensor Networkds Node Localization Algorithm Based on Improved ABC Algorithm[J].Acta Automatica Sinica,2014,5(5):974-980.
[13] 黄丽莲,周晓亮,项建弘.分数阶PID控制器参数的自适应设计[J].系统工程与电子技术,2013,25(5):1065-1069.
[14] 刘金琨.先进PID控制MATLAB仿真(第三版)[M].北京:电子工业出版社,2011.
[15] 张小凤,王孝洪,田联房,等.基于分数阶PIλ控制器的有源电力滤波器直流侧电压控制[J].电力系统自动化,2013,37(16):108-113.
[16] 谢 伟,游 敏,周玉钦.基于自适应分数阶微分的引导滤波及其应用[J].计算机应用研究,2016,34(2):1-7.
[17] 尹进田,李白雅,黄 海.基于DSP的模糊自适应PID伺服电机控制系统[J].电机与控制应用,2007,34(10):8-10.
[18] 姚舜才,潘宏侠.粒子群优化同步电机分数阶鲁棒励磁控制器[J].控制与决策,2009,24(2):162-167.
An Improved Artificial Colony Optimized Algorithm for Fractional-Order PID Controller
Hu Haitao,Gao Song,Chen Chaobo,Cao Kai
(Xi’an Technological University,Xi’an 710021,China)
It is complicated to set parameters of fractional order PID controller, the optimization results from traditional method are not only difficult to achieve but poor, so this paper put forward an improved artificial colony algorithm to complete the fractional order PID controller’s parameter setting. First, improving the searching equation and adding an elimination mechanism in artificial colony algorithm to achieve parameters’ intelligent searching. Next those parameters will be sent to the fractional order PID controller and then repeat forementioned process. Meanwhile, using the integral of absolute error index (AIE) with weights as the objective function. Finally the controller can be concluded. This paper used a nonlinear system as a controlled object, by simulation and analysis, proved the controller’ performance of improved algorithm is more better in dynamic and steady-state than the controller of traditional integer order and the controller without improved artificial colony algorithm.In addition, this new algorithm we proposed is better than not improved algorithm in the aspect of maximum overshoot, rise time and oscillation.
artificial bee colony algorithm; fractional order; optimization
2017-01-18;
2017-02-27。
陕西省教育厅科研计划项目(16JF013);陕西省工业科技攻关计划项目(2016GY-032);西安工业大学校长基金(XAGDXJJ15014)。
胡海涛(1992-),男,陕西西安人,硕士研究生,主要从事系统工程理论及应用方向的研究。
高 嵩(1966-),男,陕西西安人,博士,教授,硕士研究生导师,主要从事智能控制和多传感器信息融合方向的研究。
1671-4598(2017)07-0098-04
10.16526/j.cnki.11-4762/tp.2017.07.025
TP301.6
A
陈超波(1978-),男,浙江宁波人,副教授,硕士研究生导师,主要从事智能控制和计算机控制方向的研究。
