多移动机器人轨迹跟踪控制系统设计与实现

陈 俊, 俞 立, 滕 游

(浙江工业大学 信息工程学院, 杭州 310023)

多移动机器人轨迹跟踪控制系统设计与实现

陈 俊, 俞 立, 滕 游

(浙江工业大学 信息工程学院, 杭州 310023)

针对轮式移动机器人的轨迹跟踪控制问题，在分析了机器人运动学模型的基础上，构建多机器人的领航-追随模型；采用跟踪微分器在输入输出两端安排过渡过程，设计了一种基于多变量解耦的非线性PID轨迹跟踪控制器；搭建以Arduino Mega 1280控制板为核心的移动机器人实验平台，采用速度PID控制器以满足机器人驱动电机的实时调速要求，基于ROS提出一种结构化和模块化的多机器人控制系统；在此基础上进行实验，并将实验结果与传统PID方法控制的实验结果进行对比；实验结果验证了文章所提算法的有效性，控制器易于实现且具有一定的鲁棒性。

轮式移动机器人；轨迹跟踪；跟踪微分器；非线性PID；机器人操作系统

0 引言

轮式移动机器人是一个典型的非线性系统，其固有的非完整约束使得对轮式移动机器人的研究必须建立在非完整系统理论基础上[1]。在实际应用中，移动机器人会受到如地面不规则、轮子滑动等许多意想不到的干扰，加上Brockett定理的限制[2]，机器人的轨迹跟踪控制问题具有很大的挑战性。

针对移动机器人轨迹跟踪控制问题,国内外也已经有了很多研究成果。Back-stepping方法将复杂非线性系统分解并设计子系统的Lyapunouv函数和中间虚拟控制量，然后通过积分器后推逐步修正算法，最终完成整个控制律的设计[3-6]。自适应控制方法通过比较实际的和要求的性能指标，获取信息来修正控制器参数，适应控制目标和外部扰动等动态性能的变化[7-9]。另外还有模型预测控制[10]、滑模变结构[11]、遗传算法[12]等控制方法以及多方法混合控制策略[13-15]。但这些控制方法在不但在控制器设计和参数整定上十分复杂，同时对数据的实时性要求很高，在实际应用当中很难实现。所以，寻求一种控制效果好同时又容易实现的控制方法十分有必要。

本文根据多移动机器人的领航-追随模型，在基于Arduino的机器人平台上对机器人的轨迹跟踪控制进行了实验研究。在对多机器人轨迹跟踪系统进行状态解耦之后，考虑到非线性PID控制方法的快速性和鲁棒性[16]，尤其是其在实际应用中更易实现的特点，本文提出了一种基于非线性PID控制方法的轨迹跟踪控制器。采用最速跟踪微分器[17]安排过渡过程，来提高给定量和输出量的合理性并且更有效地提取对应的微分信号[18]。同时，以Arduino为控制系统核心搭建简单可靠的移动机器人运动控制平台，通过速度PID控制器实现底层的电机实时调速，并在ROS环境下设计多机器人软件控制系统。实验结果验证了所设计算法的有效性和抗干扰性。

1 问题描述

轮式移动机器人采用两轮独立驱动外加从动轮的差分结构，其结构示意图如图1所示。其中，XOY为全局坐标系，c点为小车的质心，d为小车质心到两轮中心的距离，r表示小车驱动轮的半径，L表示两个轮子之间的距离，(x,y)表示小车质心在全局坐标系中的位置，θ为小车的偏航角，v和ω分别表示小车的线速度和角速度。

图1 移动机器人结构示意图

(1)

针对多机器人的控制问题，在同一水平面下，两个机器人的系统结构如图2所示，其中的M1和M0分别表示主从两个机器人。

图2 多机器人跟踪系统示意图

(2)

对式(2)进行求导，由式(1)可得误差模型如(3)式所示。(3)式即为主从机器人的领航追随模型，其中xe为主从机器人的横向位置误差，ye为主从机器人的纵向位置误差。

(3)

本文所涉及的轨迹跟踪指的是从机器人以固定的横向距离差和纵向距离差跟踪主机器人的运动。在两个机器人初始位置和主机器人运动速度已知的前提下，给定期望的横向差与纵向差，设计轨迹跟踪控制器控制从机器人的线速度v0和角速度ω0，使得主从机器人的横向差xe和纵向差ye能够跟踪上给定值。

2 控制器设计

多移动机器人轨迹跟踪控制系统是一个多输入多输出系统，具有强耦合性。为了更加灵活地选取参数，使被控输出更有效地跟踪设定值，提高控制精度，对系统参数进行解耦是十分有必要的[19]。考虑到解耦过程中的计算复杂度和控制精度等因素，本文采用多变量解耦[20-21]的方式把系统解耦成x轴方向和y轴方向两个独立的单输入单输出系统。把从机器人的线速度和角速度看成是中间控制量，即令uv=v0，uω=ω0，则由式(3)可以得到：

(4)

在(4)式中取：

(5)

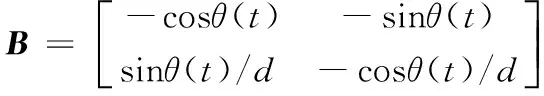
(6)

简写成如下形式：

(7)

然而，针对这样一个典型的非线性系统，面对不断变化的环境，控制器的动态品质会受到很大影响，必须设计另一个控制器提供虚拟控制量Um，以保证系统的鲁棒性。传统PID控制方法的精髓在于“基于误差反馈来消除误差”，控制器设计简单可靠且具有强鲁棒性，但直接取目标与实际的误差又常常造成初始控制力太大而使系统出现很大超调[22]。考虑到这些局限性，本文进一步设计了一种基于非线性PID方法的控制器，利用跟踪微分器安排过渡过程来提取信号的跟踪值和微分值，在保证闭环系统稳定性的同时很好地改善了传统PID控制方法的快速性和鲁棒性[23-24]。系统总体结构如图3所示。考虑到最速跟踪微分器快速、无超调、无颤振且能给出较好的微分信号的特点，非线性PID控制器采用非线性结构的最速跟踪微分器安排过渡过程，分别得到给定信号和实际信号两者的信号跟踪值及其微分信号，不仅很好地解决了超调和快速性的矛盾，增强其鲁棒性，同时也扩大了反馈增益的选取范围，更容易整定其参数[25]。最速跟踪微分器的一般形式为：

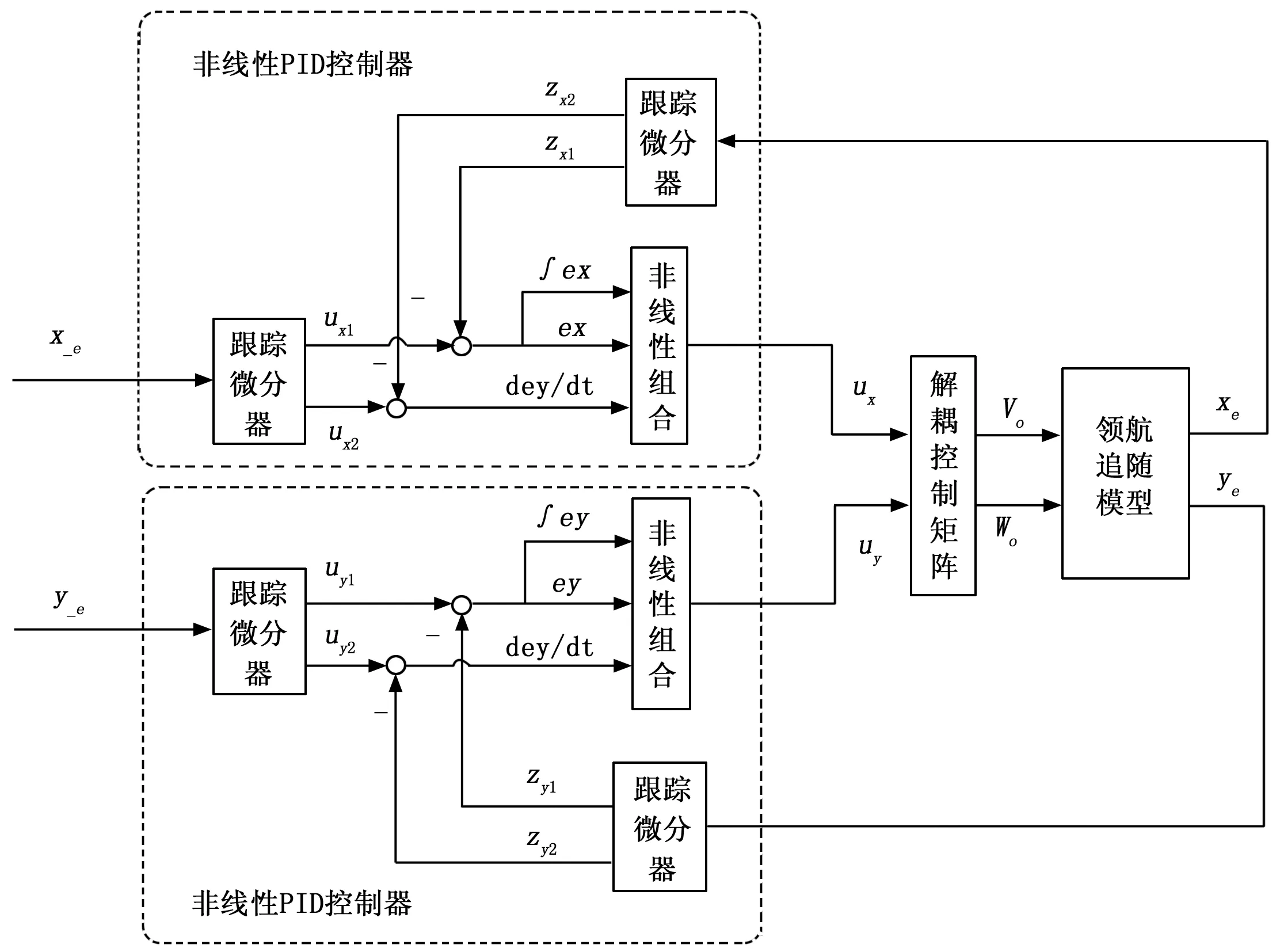
图3 非线性PID轨迹跟踪控制框图

(8)

其中:fh=fhan(v1-v,v2,r,h0)为最速控制综合函数，v为最速跟踪微分器的输入，v1和v2为输出。r为跟踪微分器的快速因子，h0为滤波因子，h为积分步长。(8)式中最速控制综合函数的算法公式如(9)式所示

(9)

以横向间距控制为例，给定信号xe_1作为参考输入，xe作为实际输出，分别将其送入对应的跟踪微分器中。ux1和ux2分别表示给定信号xe_1的跟踪值和微分值，zx1和zx2分别表示输出信号xe的跟踪值和微分值。考虑到安排过渡过程所需的设定值没有什么噪声，可以取h0=h=dt，其中dt表示系统运行的采样时间。那么就有:

(10)

产生误差信号:

(11)

取误差信号的线性组合产生状态误差反馈控制律：

Ux=βx1ex1+βx2ex2+βx3ex3

(12)

同样方法可获取纵向差控制部分的的状态误差反馈控制律：

Uy=βy1ey1+βy2ey2+βy3ey3

(13)

多变量解耦控制和非线性PID控制共同组成了多机器人系统的轨迹跟踪控制器，在保证控制效果的同时也能够分别控制x轴方向和y轴方向的被控输出，提高了系统的灵活性。

3 实验验证

3.1 多移动机器人实验平台设计

多移动机器人实验平台由两个相互独立的机器人组成，如图4所示。

图4 多移动机器人控制系统实验平台

主从两个机器人作为两个相互独立的子系统，通过PC端的WiFi信号连入同一个网中组成多机器人系统，实现信息交互。考虑到机器人操作系统(ROS, Robot Operating System)模块化、网络化和分布式的特点，本文基于ROS设计多机器人轨迹跟踪控制系统软件，实现传感器和机器人位姿信息的交互和处理，以及上位机软件的开发。其系统结构如图5所示。

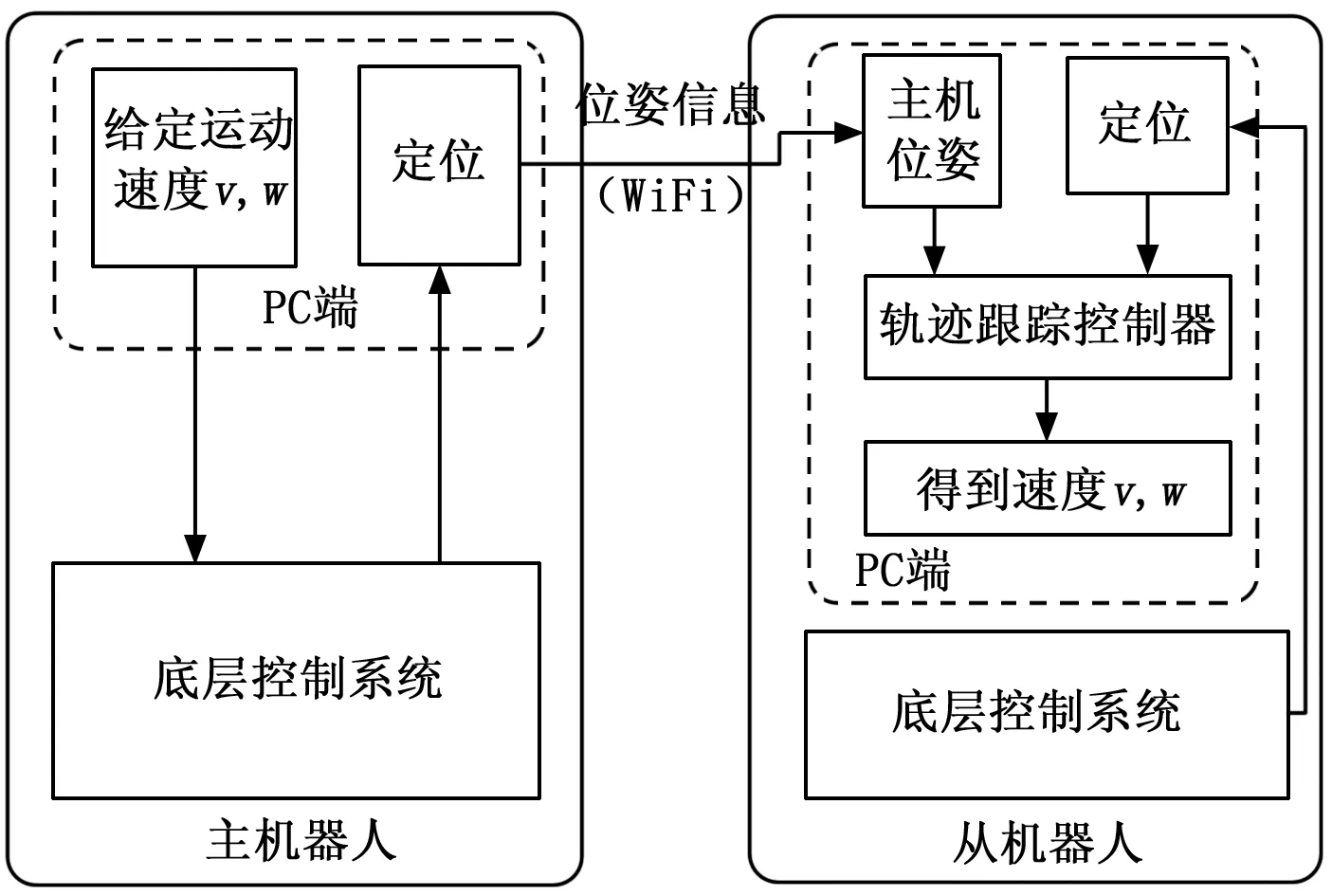
图5 多机器人跟踪控制系统结构

系统采用航迹推算的方式实现机器人自身的定位[26]，在设定主机器人线速度和角速度的前提下，给定期望的横向差和纵向差。从机器人接收主机端位姿信息之后，结合自身的位置信息以及期望距离差，通过所设计的非线性PID轨迹跟踪控制器控制从机器人的线速度和角速度，进而使得主从机器人的横向差和纵向差趋近期望值。

对于单个移动机器人来说，其硬件结构如图6所示。

图6 移动机器人硬件结构图

其中，核心控制板选用以ATmega 1280单片机为基础的Arduino Mega 1280，具有I/O接口丰富、运算速度快、存储空间大、实时性好等优点。电机驱动器采用双路大功率H桥驱动形式，4个数字I/O口同时控制2路电机运转。电机选用直流减速电机，减速比51，自带高精度的霍尔编码器，可提供输出轴每转663个反馈的脉冲信号。另外，轮胎选用136 mm外直径的橡胶轮胎。电源选用11.1 V/12AH锂聚合电池供电，配以72 W直流稳压模块(12 V@6A)，保证12 V的稳定电压。

考虑机器人底层的运动控制，采用PWM调速的方法实现电机的转速调节[27]。以采样周期内编码器值的变化量作为反馈信号，设计基于PID控制方法的速度闭环，采用传统的PID参数整定方法[28]对控制器参数进行整定，实现电机的实时调速。考虑到移动机器人的运动学约束，控制过程中引入机器人速度、加速度受限策略以排除一些不必要的干扰信号，保证机器人运动的平滑性。

设置电机速度PID控制器的采样时间tp=25 ms，参数为(kp,ki,kd)=(3,0.5,0.6)受限环节选取:

给定电机转速100 r/min，电机调速效果如图7所示，从图中可以看出，在PID控制器作用下，电机能够实时准确地跟踪给定速度。

图7 电机速度PID控制响应

基本的控制程序均在Arduino中实现，在接收到PC端发来的控制指令后，经过闭环调速系统实时调节电机转速，同时将机器人的动态信息发送至PC端，用以实时记录与监控。底层的控制系统通过USB串行通讯与PC端相连，实现数据交互。

3.2 多机器人轨迹跟踪实验

为了验证算法的正确性，在上述实验平台上进行轨迹跟踪控制实验。机器人重心与两轮之间的距离d=5 cm，驱动轮的直径dl=13.4 cm，两轮之间的距离L=28 cm，驱动轮转动一周的编码器值的变化量为1 326。

主机器人初始位置作为全局坐标系的原点，选取从机器人的初始位置(x0,y0)=(0,-0.5)。设定主机器人的运动速度(v1,ω1)=(0.1,0.1)，期望的横向纵向距离(x_e,y_e)=(0,0.5)。另外，实验开始后10 s外加一个物块增加负载，当做是外部扰动。

设置非线性PID轨迹跟踪控制器的采样时间dt=25 ms，参数为：

主从两个机器人在上位机上显示的运动轨迹如图8所示；运动过程中两个机器人之间的横向距离和纵向距离变化如图9所示；运动过程中两个机器人之间的横向距离误差和纵向距离误差变化如图10所示。

图8 机器人参数设定及轨迹显示

图9 横向距离和纵向距离的变化曲线

图10 横向和纵向距离误差的变化曲线

对实验结果进行分析，发现系统动态过程中有一定的超调量，最大超调量为10%，系统的调节时间大约在4 s左右，稳态过程中系统的稳态误差始终在5%范围内波动。同时，在外加一定干扰的情况下，系统仍能快速稳定。

为了进一步证明上述算法的优越性，设计基于传统PID控制方法的轨迹跟踪控制器，设置PID控制器的参数为：

图11和图12分别表示在传统PID控制器作用下的系统响应曲线。

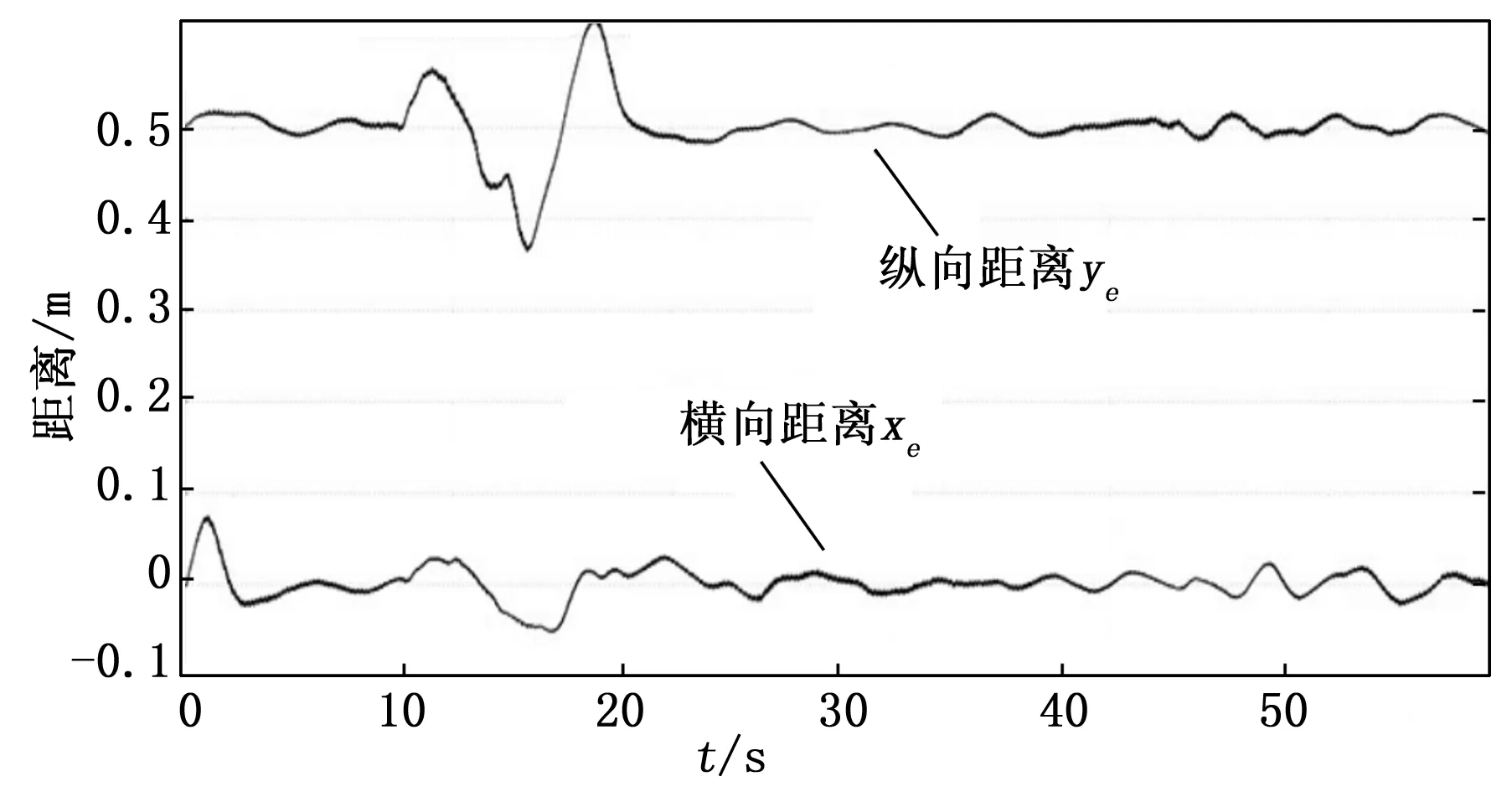
图11 PID控制器作用下的距离变化曲线

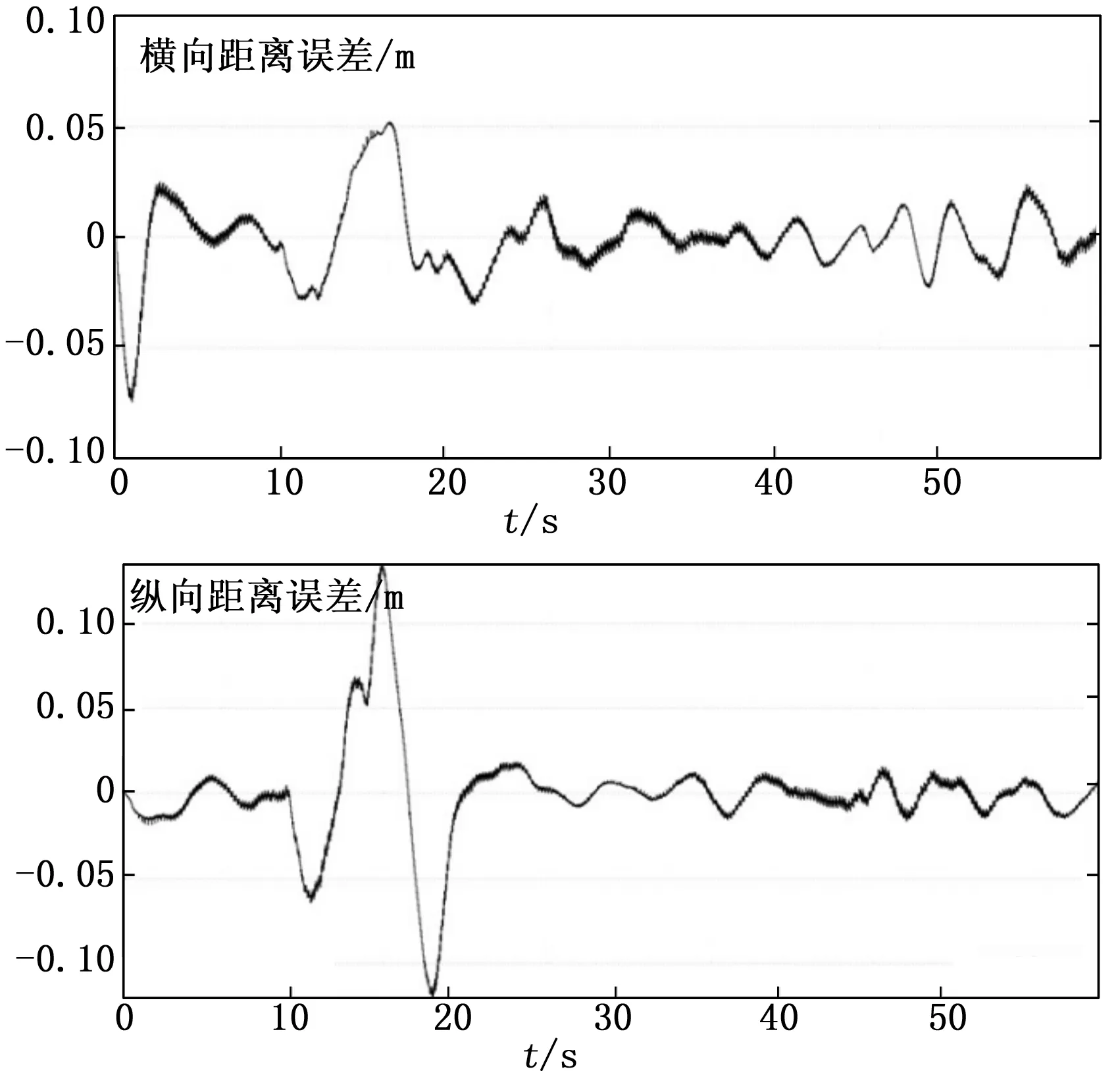
图12 PID控制器作用下的误差变化曲线

从图中可以看出，传统PID控制器作用下的系统动态性能不佳，超调偏大，能使系统保持稳定但最后稳定状态下波动幅度偏大。而非线性PID控制器在保证系统鲁棒性的同时，大大减少了超调，同时在稳定状态下也有很好地动态性能。

4 结论

本文研究了轮式移动机器人的轨迹跟踪控制问题，根据移动机器人的动态特性,得到了主从机器人的领航追随模型。设计了一种基于非线性PID方法的轨迹跟踪控制器，以最速跟踪微分器为过渡过程，解决了传统PID控制器的局限性所带来的问题。然后采用多变量解耦的方式对系统进行解耦。同时，基于Arduino控制板搭建移动机器人实验平台，机器人的速度PID控制器作为底层控制器实现电机的快速实时调速。轨迹跟踪实验表明本文提出的算法具有良好的控制效果。

[1] Kolmanovsky I, Mcclamroch N H. Developments in nonholonomic control problems[J]. IEEE Control Systems, 1995, 15(6): 20-36.

[2] Gardner R B. Differential geometric methods interfacing control theory[M]. Birkhauser, Boston, 1983.

[3] Jiang Z P, Nijmeijer H. Tracking control of mobile robots: a case study in backstepping[J]. Automatica, 1997, 33(7): 1393-1399.

[4] Kozlowski K, Majchrzak J. A backstepping approach to control a nonholonomic moblie robot[A]. IEEE International Conference on Robotics and Automation[C]. 2002: 3972-3977.

[5] 徐俊艳, 张培仁, 程剑锋. 基于Backstepping时变反馈和PID控制的移动机器人实时轨迹跟踪控制[J]. 电机与控制学报, 2004, 8(1): 35-38,43.

[6] 孟 静, 陈 罡, 高晓丁. 多移动机器人的目标跟踪研究[J]. 计算机测量与控制, 2016, 24(4): 141-145.

[7] Park B S, Yoo S J, Jin B P, et al. A simple adaptive control approach for trajectory tracking of electrically driven nonholonomic mobile robots[J]. IEEE Transactions on Control Systems Technology, 2010, 18(5): 1199-1206.

[8] Park B S, Yoo S J, Park J B, et al. Adaptive output-feedback control for trajectory tracking of electrically driven non-holonomic mobile robots[J]. IET Control Theory & Applications, 2011, 5(6): 830-838.

[9] Huang J, Wen C, Wang W, et al. Adaptive stabilization and tracking control of a nonholonomic mobile robot with input saturation and disturbance[J]. Systems & Control Letters, 2013, 62(3): 234-241.

[10] Farina M, Betti G, Giulioni L, et al. An approach to distributed predictive control for tracking-theory and applications[J]. IEEE Transactions on Control Systems Technology, 2014, 22(4): 1558-1566.

[11] Chwa D. Sliding-mode tracking control of nonholonomic wheeled mobile robots in polar coordinates[J]. IEEE Transactions on Control Systems Technology, 2004, 12(4): 637-644.

[12] Guo J, Hu P, Li L, et al. Design of automatic steering controller for trajectory tracking of unmanned vehicles using genetic algorithms[J]. IEEE Transactions on Vehicular Technology, 2012, 61(7): 2913-2924.

[13] Yanfeng G, Hua Z, Yanhui Y. Back-stepping and neural network control of a mobile robot for curved weld seam tracking[J]. Procedia Engineering, 2011, 15: 38-44.

[14] Rossomando F G, Soria C, Carelli R. Sliding mode neuro adaptive control in trajectory tracking for mobile robots[J]. Journal of Intelligent and Robotic Systems, 2014, 74(3): 931-944.

[15] Sun D, Wang C, Shang W, et al. A synchronization approach to trajectory tracking of multiple mobile robots while maintaining time-varying formations[J]. IEEE Transactions on Robotics, 2009, 25(5): 1074-1086.

[16] 尹君驰, 黄 勇. 非线性PID控制系统设计[J]. 中小企业管理与科技, 2012 (21): 209-210.

[17] 韩京清, 王 伟. 非线性跟踪—微分器[J]. 系统科学与数学, 1994, 14(2): 177-183.

[18] 韩京清. 一种新型控制器—NLPID[J]. 控制与决策, 1994, 9(6): 401-407.

[19] 池瑞楠, 胡跃明, 胡终须. 基于解耦控制的非完整移动机器人实时轨迹跟踪[J]. 机器人, 2001, 23(3): 256-260.

[20] 韩京清. 自抗扰控制器及其应用[J]. 控制与决策, 1998, 13(1): 19-23.

[21] 马永光, 郝 娜, 李鹏飞, 等. 基于自抗扰的多变量解耦控制在球磨机的应用[J]. 热能动力工程, 2007, 22(3): 297-300.

[22] 韩京清. 利用非线性特性改进PID控制律[J]. 信息与控制, 1995, 24(6): 356-364.

[23] Huang Y, Han J. Analysis and design for the second order nonlinear continuous extended states observer[J]. Chinese Science Bulletin, 2000, 45(21): 1938-1944.

[24] 韩京清. 非线性PID控制器[J]. 自动化学报, 1994, 20(4): 487-490.

[25] 韩京清, 袁露林. 跟踪—微分器的离散形式[J]. 系统科学与数学, 1999, 19(3): 268-273.

[26] 张 利, 潘承毅, 刘征宇,等. 差动驱动机器人的一种航迹推算定位方法[J]. 合肥工业大学学报(自然科学版), 2010, 33(11): 1605-1608.

[27] 邹爱成, 曹轶杰. 基于单片机的PWM直流电机控制系统设计[J]. 装备制造技术, 2014 (4): 27-29.

[28] 周 阳, 周美娇, 殷 弋. 直流电机调速系统设计及 PID 参数整定[J]. 电子科技, 2016, 29(5): 153-157.

Design and Implementation of Trajectory Tracking Control System of Wheeled Mobile Robots

Chen Jun, Yu Li, Teng You

(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023,China)

This paper deals with the problem of trajectory tracking control of wheeled mobile robots. The leader-follower model of the robots is established, then a nonlinear PID trajectory tracking controller with multivariable decoupling strategy is proposed, including two tracking differentiators(TD) at the input and output ports. To implement this algorithm, a wheeled mobile robots platform is constructed using Arduino Mega 1280 controller as the core, then the PID controller is proposed for the speed control of DC motor, and the software system is developed under the environment of robot operating system(ROS). Finally, experiments on the robot are developed to show the performance of the proposed algorithm, including the comparison with PID controller. The experimental results demonstrate the effectiveness and robustness of the algorithm.

wheeled mobile robot; trajectory tracking; tracking differentiators(TD); nonlinear PID control; robot operating system(ROS)

2017-01-03；

2017-02-27。

浙江省自然科学基金重点项目(LZ15F030003)。

陈 俊(1991-)，男，浙江杭州人，硕士研究生，主要从事移动机器人轨迹跟踪方向的研究

俞 立(1961-)，男，浙江杭州人，教授，博士生导师，主要从事网络化控制、机器人控制方向的研究。

1671-4598(2017)07-0082-05

10.16526/j.cnki.11-4762/tp.2017.07.021

TP3

A