多智能体系统的队形控制方法及应用综述
2017-08-30禹鑫何燕琳欧林林
禹鑫,何燕琳,欧林林,程 诚
(浙江工业大学 信息工程学院,杭州 310023)
多智能体系统的队形控制方法及应用综述
(浙江工业大学 信息工程学院,杭州 310023)
多智能体系统队形控制的研究主要集中于队形形成、队形保持和队形变换3个方面;首先,介绍、分析了多种队形控制方法,包括轨迹跟踪法、行动选择法、假想刚体法、网络关系图分析法、动态编队法、虚拟势场法、学习控制法和混合控制法等;其次,对移动机器人、无人机、水下机器人等多智能体系统的队形控制应用进行研究;然后,给出了近年来多智能体系统队形控制的研究进展,包括基于复Laplacian矩阵的多维空间队形控制方法,其它领域技术(云计算、图像处理等)用于队形控制的研究成果,并对基于队形控制的多移动机器人和无人机搬运作了介绍;最后,给出了当前队形控制研究中尚未解决的问题,包括队形扩展,队形稳定性,通信、传感器功能,异构多智能体系统队形控制和机械臂编队等。
队形控制;多智能体系统;编队应用
0 引言
随着社会生产的发展和科学技术的创新升级,越来越多的任务正从由人类完成转变到通过智能体来完成。随着任务复杂度的提高,对单智能体的要求也越来越高,出现了单智能体很难或是无法完成给定任务的情况,人们开始对多智能体系统进行研究。多智能体系统“是由多个智能体组成的集合,智能体之间以及智能体与环境之间通过通讯、协商与协作来共同完成单个智能体所不能解决的问题”[1]。多智能体系统有很多优势,如提高完成任务的效率,较大的冗余,更好的容错性、鲁棒性、经济效益等等,因此多智能体系统的规划、协调和竞争等研究在控制领域和人工智能领域获得了广泛的关注[2-4]。在较多任务中,需要多智能体在运动和完成任务时保持一定的队形,这样不仅能够充分获取周边环境信息,还能提高工作效率,增强系统的鲁棒性,因此多智能体的队形控制研究受到了多方面的关注。
队形控制指“多个智能体组成的团体在向特定目标或方向运动过程中,相互之间保持预定的几何形态(即队形),同时又要适应环境约束(例如避开障碍物)的控制问题”[5]。近十几年来,国内外在队形控制方面进行了大量的研究,研究内容主要集中在以下3个方面:第一是队形形成,主要研究多智能体如何自主形成目标队形的问题;第二是队形保持,研究多智能体实现队形后,在运动和作业时保持队形不变的问题;第三是队形变换,研究多智能体从一种队形转换到另一种队形的问题,包括主动变换和被动变换两种方式,主动变换往往是由于任务要求,需要多智能体变换成另一种队形从而能够完成或是更好的完成任务,被动变换一般是由环境造成的,使得多智能体不得不做出队形变换,此时的队形变换主要是为了躲避障碍物以便多智能体能够顺利进行任务。
队形控制的应用十分广泛,在工业、军事、航空等领域拥有很好的前景。在工业制造中,例如通过多智能体系统进行大型物体或是危险物品的搬运,对多智能体的队形位置有一定的要求,需要实现搬运过程中负载平衡,避免出现某一智能体承受过多负载的情况,同时还提高了效率,保障人类安全。在军事领域,自古排兵布阵是很有学问的,在现代军事装备下,通过保持合理合适的队形,可以做到攻守兼备,大大提高了军事实力;在危险、恶劣环境下,通过智能体代替士兵的方式,进行诸如探索未知环境、排雷、巡逻、侦察等任务,能够最大程度的保证人员安全,同时完成任务。在航天领域,航天器如地球卫星等在一定程度上可以看成是智能体,因此航天器的编队也是属于多智能体编队领域,通过将卫星、探测器等航天器进行编队探索宇宙,不仅能降低成本,提高系统的可靠性,还可以完成许多单个航天器无法实现的任务。在某些特殊情况下,可以进行地震或是水灾后的营救、物资发放。民用上可以进行农作物的播种、播撒(农药)、收割。因此,对多智能体系统队形控制的研究在多智能体控制领域得到了广泛的关注。
1 国内外研究现状
随着在工业领域中计算机技术,人工智能技术,自动化控制技术的飞速发展,多智能体系统的队形控制已经成为国内外的热点前沿研究领域,每年在国内外主流学术期刊以及重要国际、国内控制会议上都有许多关于多智能体系统队形控制的文献出版。近几年提出的主要编队方法有轨迹跟踪法,行动选择法,假想刚体法,网络关系图分析法,动态编队法等。
关于不同编队方法的国内外研究现状将分别加以详细阐述。
1.1 轨迹跟踪法
轨迹跟踪法是一种由领航智能体和跟随智能体组成的编队方法,领航者采用直接指定的方式,需完成跟踪给定轨迹的任务,余下的智能体作为跟随者跟踪领航机器人轨迹,同时与领航者之间保持相对位置或是保持一定的距离[6]。该方法将队形控制的问题转换成轨迹跟踪的问题,主要研究距离和角度的相对误差,与控制理论知识的误差概念相近,因此也可以用控制理论的知识来研究该方法。
Kumar教授是较早对轨迹跟踪法进行研究的人员,对这种方法的主要工作包括:提出了l-φ和l-l两种跟踪领航者轨迹的经典编队模式,提出输入输出线性化方法[7],之后在l-φ和l-l两种模式基础上实现了任意队形切换[8-9]。除了以上两种策略实现轨迹跟踪法的编队,还有其它的控制策略能够实现编队,包括基于李雅普诺夫直接法的运动控制方法[10],转换策略[11]等等。其他研究人员也对这种方法进行了研究。Soorki等[12]将Kumar提出的两种编队模式结合,提出了l-l-φ的编队方式,利用反馈线性化分析方法,对相对于领航者的跟随者进行了相对距离和方向角稳定性分析,针对机器人的一阶和二阶运动学模型设计了队形控制器,同时将障碍物作为一个虚拟领航者,提出了快速避障的方法;Peng等[13]采用了轨迹跟踪法的思想研究编队问题,通过简单的输入输出线性方法推导出4个控制律研究了编队问题;Wu等人[14]研究了基于跟随领航动力学模型的编队问题,采用线性化方法设计了速度控制器,将队形控制问题转换成追踪问题实现编队;Guo等[15]给出了双领航者的控制策略,规定只有领航者知道行进路线,其余每个智能体有且只有两个邻居智能体并组成三角形队形,对三角形的组成规则进行了约束,构成了串级连接,能够用于大规模编队;日本学者Choi等[16]考虑到实际环境和噪声会对传感器数据产生影响,导致队形不稳定,因此对轨迹跟踪编队控制下的多智能体系统队形进行了PID控制算法的研究,提高了队形的稳定性。
轨迹跟踪法只需要给定领航者的行进路线,就能够控制所有智能体形成队形,不需要进行复杂的数学分析。此外,该方法能够进行扩展,即通过指定多个多级领航者形成大规模的队形,但队形的主领航者只有一个,其余领航者根据上下级关系保持跟踪上一级的队形领航者,其余跟随者按照队形要求跟踪各个次级领航者,从而实现规模扩展。这种方法也有缺点:整个队形依赖领航智能体[17-19],队形没有反馈机制。研究人员提出了一些解决办法。针对领航者出现故障的情况,最直接有效的解决方法是更换领航者。曹志强等人[20]就对“Leader更换”的方法进行了研究,即当领航智能体无法继续执行任务时,按设定的规则从余下智能体中选出新的领航者继续执行接下去的任务,解决了领航智能体出现故障时队形控制的问题;针对缺乏反馈机制的问题,Kumar等人采用反馈线性化技术克服了该缺点[7],并以智能体之间不同的拓扑位置关系作为依据,设计了适合不同情况的3种控制器[11-21]。
1.2 行动选择法
行动选择法很早就被用于计算机仿真,研究动物的行动,如鸟类、鱼类的聚集行动。Balch和Arkin首次将行动选择法运用到多智能体队形控制领域,设计了一系列基本行动,实现多智能体系统编队、避障并最终到达目标点[22]。行动选择法“主要是通过对智能体基本行动以及局部控制规则的设计使得智能体群体产生所需的整体行动”[23]。该方法的核心是行动和行动选择,因此如何定义行动和行动选择机制十分重要。行动往往是一些简单的基本动作,主要包括了避碰、避障和保持队形等等,且都有各自的触发条件和实现目标,“当智能体传感器接收到外界环境刺激后,根据传感器的输入信息做出反应,并输出反应向量作为该行动的期望反应(如方向和运动速度)”[5]。
对行动的设计可以根据已知任务中可能会遇到的情况进行设计,同时考虑智能体是否能够执行该行动。相比行动设计问题,行动选择机制的研究更有意义,行动选择机制目前主要有3种[[22,24]:第一种是行动抑制法,基本思想是对行动按照规则制定优先级,虽然各个行动之间是相互独立的,但是在编队和运动过程中,行动之间会发生时间上的冲突,如当智能体向目标前进的过程中遇到了障碍物,此时的智能体最应该采取的是避障行动,但当前执行的是向目标前进的行动,为了解决这样的冲突,可以通过设定优先级解决冲突问题,即高优先级的行动抑制低优先级的行动。第二种是加权平均法,行动抑制法用数学语言描述就是行动权值大小的问题,但是只有两种权值0和1,因此有可能会造成控制不平滑,加权平均法是将各个行动的输出向量乘以一定的权重求出矢量和,其权值的大小对应行动的重要性,经正则化后作为智能体的输出,是在充分考虑行动的重要性后再进行的行动选择,可以得到较好的结果。第3种是模糊逻辑法,该方法本质是加权平均法的变形,根据具体情况确定权值的大小,按照模糊规则综合各个行动的输出,从而确定智能体的输出。
行动选择法中,智能体的最终行动取决于基本行动,基本行动的选择依赖于其它智能体的信息,因此队形具有明确的反馈机制;当多智能体系统需要对多个竞争性目标进行整合时,只需通过制定的规则选择行动和权重,就能够快速得出控制策略;从本质上来说,这是一种分布式的控制方法,可以进行规模扩展。该方法的主要缺点在于行动难以量化,很难从数学上进行性质(如稳定性)分析。
1.3 假想刚体法
Tan和Lewis[25]是最早提出假想刚体法的,当时是为了解决多智能体系统协作的问题,该方法的基本思想是,将整个队形作为一个假想的刚性结构体进行研究。刚体在空间中运动时,其上面每一点的位置虽然都在变化,但是点与点之间的相对位置是保持不变的,如果将这些点看作是智能体,那么当这样的刚体运动时,智能体在刚体作为参考的坐标系下的坐标是不变的,即多智能体系统能够组成具有一定几何形状的队形并且保持不变,这些智能体共同形成了一个假想的刚性结构,这样的结构称为假想结构。
假想刚体法进行编队的本质是智能体跟踪刚体上对应的期望点,每个智能体的期望点可以通过对目标队形的分析计算得到,将编队的问题转换成了跟踪的问题,但又不同于轨迹跟踪法的跟随者跟踪领航者轨迹的跟踪,假想刚体法的跟踪是各个智能体跟踪通过队形分析得到的相应的轨迹,此外,轨迹的获取需要其余智能体的信息,因此具有反馈机制。有学者就是将编队问题转换成跟踪问题,以假想刚体法分析计算得到智能体期望点的路径,采用反步法技术,设计了非线性控制算法进行队形控制[26]。当机器人规模扩大时该怎样进行编队呢?Jian等[27]先以多智能体系统的空间分布将智能体分成多个群集,然后对每个群集的运动轨迹进行规定,并设计了基于状态反馈的控制率用于在限定时间内稳定转向角度误差和位置误差。Ren等[28]采用这种方法研究队形的精确控制,提高系统性能同时保证了系统的稳定性。
假想刚体法容易描述整体行为,具有队形反馈机制和较高的控制精度,但在实际应用中,反馈机制和高精度控制都需要高通信质量和高计算能力作为代价。
1.4 网络关系图分析法
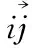
Desai等人是较早采用关系图对队形控制进行分析的研究人员,在文献[8]中采用有向关系图来表示编队问题中多智能体系统的拓扑关系,并对队形变化问题进行了研究。之后,Desai及其团队将智能体间的控制关系图用有向无环关系图进行描述,并设计了控制策略,以枚举所有可能情况的方式实现任意队形切换[9]。Wang等人[29]研究了基于有向和切换拓扑的线性队形控制方法。Lafferriere等人[30]使用代数图知识对队形的稳定性进行分析,智能体之间的信息交换通过预先设定的(无向)通信关系图G进行,仅仅以通信获得的关于智能体状态的相对信息作为反馈控制,证明了只要通信关系图G一直是连通的,则线性稳定反馈就一直存在,此外还对编队收敛速率受到通信图G的李雅普诺夫最小正根的大小的控制进行说明。Azuma等人[31]采用假想刚体法进行编队,重点研究了队形的网络结构,结合刚性图的知识,提出了只要网络关系结构是刚性的,那么队形控制就具有容错能力以应对智能体失联的情况。王祥科等人对关系图分析法的编队方法进行了较为详细的总结:基于关系图进行多智能体系统队形设计及队形控制策略设计;“代数图论借助线性代数理论研究图的表示、变换和性质等”;刚性图用来研究队形变换的问题[32]。
网络关系图分析法的数学属性使得该方法在数学分析上很有优势,也可用于分析大规模的编队问题,如利用数学知识可以进行队形稳定性、收敛性等性质的研究,但分析过于理想化,实际中碰到的问题较难用数学语言表示。
1.5 动态编队法
对编队控制的研究,大多数的研究前提是在已知环境、静态环境、同构智能体等条件下,研究的编队控制问题集中在形成队形和队形保持上,但实际环境复杂多变,更有可能发生突发状况,如对未知环境的搜索,地形复杂,障碍物也可能是动态的,队形控制的研究成果很难有较好的实际效果,因此,如何才能让编队更好的适应变化的环境引起了研究人员的思考,动态编队得到发展。对动态编队很难进行定义,但进行研究的目的是为了控制编队能够更好的适应复杂的环境,积极应对环境的变化。
日本学者Kohata、Yamaguchi等人较早研究动态编队,主要是为了解决实际的多智能体系统搬运问题,他们选择在FAMOUS和CFS系统的基础上进行改进,根据当时通过传感器等获得的环境信息,动态改变智能体的控制模块,以重新分配智能体角色的方式进行队形切换,实现动态编队[33-34]。杨丽等人以环境信息作为约束条件,“提出了一种在不确定环境下对多智能体系统进行动态编队的控制方法,解决了输入输出反馈线性化方法中因离轴点造成的问题,实现了包括线性队形在内的队形控制,并将复杂的编队问题分解成若干组两个智能体之间的协调问题,通过建立队形、保持队型、编队避障保持智能体之间的指定相对信息,躲避在行进中可能出现的障碍物”[35]。张瑞雷等人[36]将环境条件设计成更贴近实际的三维地形,研究了异构多智能体系统在该环境条件下的混合动态编队,利用反步法和李雅普诺夫函数对构建的轨迹跟踪系统模型进行轨迹跟踪器的设计,实现了不同运动学模型智能体的混合动态编队控制。Li等人[37-38]结合图论知识,利用动态交互拓扑研究了编队问题,采用了基于带鲁棒性的自适应神经网络控制的局部控制方法,通过动态选择编队方式实现动态编队,不仅实现编队任务,同时还能躲避障碍物,适应不同环境。Hou等人[39]将所有智能体限制在一定的几何图形内,以几何图形的方式运动,提出了一种动态区域编队控制方法,不仅能够按比例将图形变大或缩小实现避障,还能够在运动中改变几何图形以适应变化的环境。Ballard及其团队[40]探索实施了一种新的分布式策略进行动态变换队形控制,目的是为了智能体能够适应队形的形状和大小,此外在加入新的智能体之后,原有的形状也不发生改变。学者Low[41-42]以假想刚体法为基础,结合轨迹跟踪控制系统,对多智能体系统的队形控制进行了研究,实现动态编队控制。
1.6 其它队形控制方法
国内外学者还提出了虚拟势场法、学习控制法、混合控制法等队形控制方法。
(1)虚拟势场法。该方法来源于物理学中的电子在电场中运动,是Khatib在1986年提出的[43],其基本思想是假定智能体在一个虚拟的力场中运动,目标点产生吸引力,力的大小随着与智能体距离的减少而减小,障碍物产生排斥力,力的大小随着与智能体距离的减少而增加,吸引力、排斥力用势场函数描述,在这两种力的合力作用下,智能体将沿着最小势能方向运动。Song等人[44]提出了一种基于势函数的有效实现护卫队形和避障的控制算法,根据任务要求的不同,设计了3种势函数,并在此基础上设计了分布式控制律,该控制律不仅能够实现预期队形,还能保证在队形行进中避碰、避障。虚拟势场法计算简单,能够进行实时控制,对空间的避障、避碰问题很有效[45],但势场函数设计比较困难。
(2)学习控制法。该方法的基础是学习控制,针对的是重复性较高的任务,如工厂物件的编队搬运、安全巡逻任务等等。对多智能体系统队形进行预期编队,通过学习控制实现大致的预期队形,随着学习次数的增加,队形精度、运行效率都会得到大幅度提高[46],适用于重复性高的任务,学习花费的时间与任务复杂度成正相关性,缺点是当运行环境发生变化影响任务时,多智能体系统需要重新进行学习,方法不灵活,时间成本较高。
(3)混合控制法。上面提到的编队形控制方法都是单一的控制方法,每种方法都有各自的优缺点,面对复杂多变的环境,单单采取其中某种方法是不能满足需求的,因此研究人员开始将两种或是几种方法混合运用或是借鉴优化,取长补短,以便实现更好的队形控制。例如,轨迹跟随法可以实现准确、稳定的队形,但对动态环境适应能力较差,而行动选择法对动态的环境适应能力强,但在队形稳定性上存在不足。Zhao等人[47]结合了轨迹跟随法和虚拟势场法两种方法,控制多智能体系统形成了一个“圆”的队形,用于实现追捕任务;Kishorekumar等人[48]采用虚拟势场法对领航智能体导航避开障碍物,对跟随者智能体采用l-φ的方法进行控制,从而实现编队并能够避障。
2 多智能体系统队形控制的应用研究
对多智能体系统队形控制进行实际应用,研究人员通常会采用移动机器人进行研究。移动机器人拥有多种传感器,能进行通信交换数据,具有很好的机动性和灵活性,通过设计算法就能够表现出一定的智能。用移动机器人进行队形控制的研究应用十分广泛。在对未知环境进行探索时,多移动机器人通过控制形成队形,每个机器人在行进过程中探测环境的一部分,通过分享数据获得较为全面的环境信息,有利于人们快速熟悉环境;工业生产中,通常会需要搬运一些大型物件,对多移动机器人的位置分布有一定的几何要求,同时需要平衡负载,在一些特殊的环境下(如核反应堆内部)进行搬运,队形的控制要求更加严格。近年来,计算机科学的发展、机器人的发展都给队形控制研究注入了新的活力,出现的新型机器人拓展了队形控制的研究。
无人机是近年来研究的热点,以用途广泛,成本低,无人员伤亡风险,生存能力强,机动性能好,使用方便等众多优势吸引了一大批专家学者对其进行研究,无人机编队便是研究方向其中之一,研究人员研究较多的无人机是四旋翼飞行器。对无人机的研究,比之前的移动机器人的研究难度要大,也更有挑战性。首先,移动机器人的研究往往是两维平面,而无人机则是三维立体的研究,维度上增加了,需要考虑的影响因素也增加了,如无人机自身的平衡性。Mercado等人[49]使用轨迹跟踪法的编队方法,利用队形误差用滑模控制控制跟随者保持与领航者的相对位置,从而维持队形;Hamed等人[50]也用轨迹跟踪法,设计了模糊逻辑控制器控制跟随者,将跟随者的速度和姿态最小化编队误差来解决编队问题,该方法还能够实现未知非线性运动学的固定翼无人机的任意三维编队;Rui[46]同样采用了模糊控制器对多无人机进行编队控制,并用强化学习算法——Q学习算法对参数进行调整,提高控制精度。Luo等人[51]研究了队形保持和队形变换问题,采用PID控制方法进行队形保持,对于队形变换则是考虑到变换中可能出现的碰撞问题,设计了控制策略解决问题。针对固定翼无人机的特点,袁利平等[52]利用局部相对信息,提出了一种基于信息一致性的分散化编队飞行策略,即利用无人机之间的相对速度和相对航向信息进行速度和航向的同步,利用无人机之间的相对位置信息进行编队形成和队形保持。
除了对无人机进行研究,研究人员也对水下机器人编队控制进行研究。地球绝大多是水覆盖的,海洋资源很丰富,但因目前技术有限,人类对海洋的研究进展缓慢,通过对水下机器人的研究可以加快对海洋的探索。水下因其自身的特点,机器人之间不得不通过网络进行数据传输,但在数据传输时会存在通信延迟的问题,Millan等人[53]就注意到了这个问题,研究了在通信时延的情况下,水下机器人的编队控制问题;李一平等人[54]考虑到水下环境复杂,跟随者可能出现异常状态,提出了基于跟随者状态反馈确定领航者的策略,并在实现了一个领航者、3个跟随者的队形形成和保持的情况下,将控制策略推广到了N个跟随者的情况;Guohua等人[55]采用轨迹跟踪法进行编队,基于反推控制和生物启发神经网络研究了三维队形控制和避障问题。
3 多智能体系统队形控制的研究新进展
3.1 基于复Laplacian矩阵的多维队形控制方法
林志赟教授带领的团队将拉普拉斯算法从实数域扩展到复数域,对二维及更高维的队形控制方法进行了研究,获得了许多研究成果。多智能体系统实现一维编队的条件是当且仅当实数Laplacian矩阵有一个零特征根,或是队形关系图中存在一个根,从根出发其余各节点都可以到达[56-58]。对实数Laplacian矩阵有了一定的研究之后,该团队用复数Laplacian矩阵,研究了无向、有向拓扑结构下的多智能体队形控制,提出相似编队的概念,在此基础上,还研究了切换拓扑网络结构下的队形控制问题。
基于无向拓扑结构,通过复Laplacian矩阵和空间拓扑结构来描述队形控制问题,在此结构下得到了队形形成的代数几何条件,即图是双根的,并且还得出只受形状限制的相似队形位于满足一定秩条件的复Laplacian矩阵的零空间内,然后又在复Laplacian矩阵的基础上,设计了基于相对位置信息的分布式控制策略,同时能够保证其全局稳定性[59]。考虑多智能体系统的传感能力有限,环境复杂度等问题,研究不能局限于无向拓扑结构,进而研究了有向拓扑结构下队形控制问题,其研究思路与无向拓扑结构相同,并得到了相同的结果,是对之前结果的完善[60]。
前面的工作主要是固定拓扑结构下进行的研究,很自然就会对切换拓扑网络结构下的队形控制的研究。通过之前的研究可知,队形能够形成的充分必要条件是拓扑结构是双根的,因此,假设系统是在一组全部是双根的拓扑图中进行切换。假定每个智能体只能获得周边传感信息,考虑到物理传感约束、智能体运动超时的情况,系统的传感图是有向并且时变的,这就很难进行编队控制,于是在假设传感图在某些情况下可以转变的前提下,提出了一种线性切换控制方法用于编队控制,并进行了稳定性分析[61]。之后研究了有向切换拓扑情况下二阶智能体三维编队耦合控制的问题,目的是控制双积分动力学模型的跟随者群体和领航机器人群体耦合,形成一种单一全局刚性编队[62]。
3.2 基于云计算和图像处理的队形控制研究
云计算、图像处理等其它领域的技术发展也为队形控制研究提供了新思路。Turnbull等人[63]利用云计算对多智能体系统进行了队形控制;有学者通过智能体自身携带的摄像头,实时进行图像处理,获得相对信息从而进行队形控制[64],或是利用视觉反馈进行研究编队问题[65]。Wang等人[66]基于递归神经网络研究多智能体系统的最优编队问题,采用图形理论描述目标队形,该理论能够生成一系列的可行队形,最优队形意味着从一系列可行队形中寻找到与目标队形最小距离的队形,因此将编队问题转换成最优化的问题;特别的,当所有智能体是同构机器人时,每个智能体的目标位置是可变化的,此时的队形最优又成了组合队形最优的问题,这类问题通过借助补偿法可以近似成凸优化问题进行解决。张洪亮[67]采用分布式层次控制结构研究多智能体系统编队问题,设计了基于声纳传感器(获得周围信息)和多智能体系统通信的队形保持方法。
3.3 基于队形控制的多移动机器人搬运
多移动机器人编队应用十分广泛,在军事、工业生产、航空航天、农业生产等领域都有很好的前景,能够实现搬运、侦察、巡逻等多项任务。搬运是实际生产生活中涉及面最广、应用也是最频繁的任务,因此以该任务作为说明对象对多移动机器人编队应用进行介绍。
实际搬运中参与搬运任务的可能是移动机器人,也有可能是移动机械臂,或者是带有手抓的移动机器人。Dalfior等人[68]研究多移动机器人编队控制实现协同物体搬运,研究的重点是如何让机器人与物体一直保持接触,并且协调它们的运动完成搬运到目标地点的任务,通过设计编队控制器,将负载当做虚拟领航机器人,控制多移动机器人形成队形,并采用一种非线性位置控制器用于定义负载到目标点的移动。Moon等人[69]研究协同完成推箱子任务,为了两个移动机器人在推箱子的过程中保持一定的队形,定位系统实时获得各个机器人的位置信息,通过计算控制速度。Bai等人[70]采用移动机械臂研究协同搬运问题,需要搬运的有效负载是可变化的,用渐变的非线性电势能建模移动机械臂和负载之间的接触力,机械臂和有效负载收敛到相同的速度才能完成搬运,搬运的问题就可以近似当成编队控制问题。Eoh等人[71]利用多移动机器人协同编队进行重物体的搬运,该团队成员认为物体搬运能否成功与机器人编队有很强的关联,提出了基于推和拉(抓)两种行为的pusher-puller队形。作为pusher的机器人在物体后面推,作为puller的机器人在前面拉。Zhaohui等人[72]研究多个机器人搬运重物时,对物体质量也进行了考虑,并假定物体是刚性的,移动机器人有手抓且能紧紧抓住物体,采用分散控制技术保证搬运过程中所有机器人手抓之间的相对位置保持不变,完成搬运任务。之后又考虑环境中可能会有参数不确定的情况,结合神经网络在线学习技术,实时逼近系统的动力学模型,来实现搬运。
考虑到空中搬运,人们在以前研究时往往采用直升机作为研究对象,随着无人机的出现,专家学者开始将目光转向无人机搬运。当出现如地震、泥石流、山体滑坡等自然灾害,路面物资运输往往受阻,人工物资运输效率低下,空中投掷物资不精确,常常出现物资失踪的情况。无人机小巧灵活,无人员伤亡风险,成本低,能低空飞行,可在复杂区域登陆,采用无人机运输能够很好的解决物资运输的难题。Michael等人[73]研究控制多四旋翼无人机进行缆绳运输负载的问题,证明了因单边张力约束导致系统欠驱动,依然能够控制无人机将负载运输到指定的位置;Lee[74]重点研究刚性负载的跟踪控制,负载与任意数量的无人机通过刚性线缆连接,构造了一个几何控制器,控制负载渐进的跟踪给定期望轨迹,该方法独到之处是将刚性负载、链接和无人机之间的耦合动力明确地合并到控制系统设计和稳定性分析中;Lee与Farhad[75]合作研究了任意数量的四旋翼无人机通过软电缆连接刚性负载,提出了一种几何非线性控制器将刚性负载运输到指定地点,并将所有的连接电缆垂直对齐。
4 尚未解决的研究问题
4.1 队形扩展
对队形进行扩展包括两方面:数量和维度。目前很多队形控制研究方法面向的都是小规模的多智能体系统,运用到大规模的系统中会出现各种问题,特别的,当智能体数目是动态变化时,如智能体发生故障无法执行任务需要退出队伍或是有新的智能体需要加入队伍中时,又该如何进行队形控制;当前很多的研究都是局限在二维平面上,对智能体在更一般的三维空间中的队形控制研究较少,随着无人机、水下机器人等新型智能体的发展,三维编队控制的研究也显得越来越迫切。
4.2 队形稳定性问题
多智能体系统的队形控制中,队形的稳定性是研究者广泛关注的一个方面,主要包括了多智能体系统能否实现稳定的队形和运动过程中队形能否保持稳定两方面。此外,当环境发生变化,队形还能否继续稳定保持,这些都是在设计控制算法是需要考虑的问题。目前关于队形稳定性的研究处于理论性阶段,需要大量的实验进一步论证。
4.3 通信、传感器功能受限
随着计算机技术的发展,通信的重要性越来越重要,也是多智能体系统队形控制的基础,在进行理论分析时,一般将通信理想化,但当理论成果运用到实际时,通信就要考虑很多问题,如数据传输的时延问题、带宽限制、数据丢包、通信范围等等,这些问题对多智能体系统的队形控制是有很大影响的。除了通信理想化,智能体的传感功能也会做理想化处理,即多智能体系统不仅能实时获得周围信息,而且数据准确,但在实际应用中,除了受到智能体自身传感器的限制,诸如感知范围有限、获得数据存在时延、数据精度不足等,还会受到环境噪声的影响。此外,一些智能体自身的信息(如速度和加速度)是无法精确获取的。因此,在通信和传感器功能受限条件下的队形控制问题也是应用到实际环境中需要解决的问题。
4.4 异构多智能体系统队形控制研究
在目前现有的队形控制研究成果中,绝大多数的研究都是针对同构智能体进行的,采用同构智能体进行研究有其优势:所有智能体的动力学特性相同,数学分析、建模都比较简单,且拥有相同的功能,能够相互替换完成任务。但在实际应用中,以远距离运输为例,部分智能体编队组成导航组进行导航,部分智能体编队组成搬运组进行运输,实现的功能不同,队形设计的侧重点不同,相互之间的动力学特性也存有较大的差异。现在社会分工越来越细,专业化的智能体往往比综合性智能体有更好的经济效益,这也就意味着智能体之间的动力学特性等存在差异,在面向实际应用方面,异构多移动机器人的编队控制也有很大的发展前景。
4.5 机械臂编队研究
当前研究的编队控制对象几乎都是轮式机器人、无人机、水下机器人等,很少有对机械臂进行编队研究,机械臂都是固定式的,当机械臂的操作对象在移动时,就可以将机械臂看成是移动的,机械臂的编队研究也有实际应用。比如喷漆操作,当需要对部件进行喷漆处理时,不同的部位需要喷上不同的颜色,当机械臂组成一定队形时,就能实现该任务。
5 应用前景展望
多智能体系统的队形控制涉及的内容十分广泛,具有很大的应用前景。在对海底环境勘探时,水下机器人组成特定队形,每个机器人在行进过程中探测环境的一部分,通过通信分享数据获得较为全面的全部环境信息,有利于加快人们对海底环境的了解。但是,海底环境复杂,多机器人系统保持良好的稳定性和良好的通信状况是实现水下机器人勘探海底环境的重要前提。在工业生产中,通常需要搬运一些大型物件,多移动机器人可以很好地完成这个任务。然而,在远程搬运中,就需要有异构多智能体,一部分负责导航,一部分负责搬运。因此,异构多智能体系统队形控制的研究将对远程搬运起到很大的作用。无人机的快速发展,促进了人们对空中搬运的研究,当发生地震、泥石流等自然灾害时,无人机空中搬运将大大降低救援成本和救援人员伤亡的可能性。因此,对多智能体系统三维编队控制的研究也越来越迫切。此外,多智能体的队形控制还能够应用于排雷、定点巡逻、灾后营救、农作物播种等许多领域。随着科技的不断发展,多智能体系统的队形控制方法与应用水平将得到不断地提高,队形控制也将在更多的领域中得到实际应用。
[1] 刘 佳, 陈增强, 刘忠信. 多智能体系统及其协同控制研究进展[J]. 智能系统学报, 2010, 5(1): 1-9.
[2] Yang F, Liu S, Liu F. Cooperative transport strategy for formation control of multiple mobile robots[J]. Journal of Zhejiang University SCIENCE C, 2010, 11(12): 931-938.
[3] Galuszka A, Swierniak A. Planning in multi-agent environment using strips representation and non-cooperative equilibrium strategy[J]. Journal of Intelligent and Robotic Systems, 2010, 58(3-4): 239-251.
[4] Liu S, Sun D, Zhu C. Coordinated motion planning for multiple mobile robots along designed paths with formation requirement[J]. IEEE/ASME Transactions on Mechatronics, 2011, 16(6): 1021-1031.
[5] 苏治宝, 陆际联. 多移动机器人队形控制的研究方法[J]. 机器人,2003(1):88-91.
[6] Soltani N, Shahmansoorian A, Khosravi M. Robust distance-angle leader-follower formation control of non-holonomic mobile robots[A]. 2014 Second RSI/ISM International Conference on Robotics and Mechatronics (ICRoM)[C]. 2014: 24-28.
[7] Desai J, Ostrowski J, Kumar V. Controlling formations of multiple mobile robots[A]. Proceedings of the IEEE International Conference on Robotics and Automation[C]. 1998: 2864-2869.
[8] Desai J, Ostrowski J, Kumar V. Modeling and control of formations of nonholonomic mobile robots[J]. IEEE Transactions on Robotics and Automation, 2001, 17(6): 905-908.
[9] Desai J. A graph theoretic approach for modeling mobile robot team formations[J]. Journal of Robotic Systems, 2002, 19(11): 511-525.
[10] Li X, Xiao J. Robot formation control in leader-follower motion using direct Lyapunov method[J]. International Journal of Intelligent Control and Systems, 2005, 10(3): 244-250.
[11] Fierro R, Das A K, Kumar V, et al. Hybrid control of formations of robots[A]. Proceedings of the IEEE International Conference on Robotics and Automation[C]. 2001, 1: 157-162.
[12] Soorki M N, Talebi H A, Nikravesh S K Y. A leader-following formation control of multiple mobile robots with active obstacle avoidance[A]. Proceedings of the 19th Iranian Conference on Electrical Engineering (ICEE)[C]. 2011: 1-6.
[13] Peng T, Li S. Formation Control of Multiple Wheeled Mobile Robots via Leader-Follower Approach[A]. 第26届中国控制与决策会议论文集[C]. 2014.
[14] Lijuan W, Hui W. Multi-robot formation control and simulation[A]. Proc of the 25th Chinese Control and Decision Conference (CCDC)[C]. 2013: 2830-2833.
[15] Guo J, Lin Z, Cao M, et al. Adaptive leader-follower formation control for autonomous mobile robots[A]. American Control Conference (ACC)[C]. 2010: 6822-6827.
[16] Choi I, Choi J, Chung W J. Leader-follower formation control without information of heading angle[A]. IEEE/SICE International Symposium on System Integration (SII)[C]. 2012: 842-846.
[17] Mesbahi M, Hadaegh F Y. Formation flying control of multiple spacecraft via graphs, matrix inequalities, and switching[J]. Journal of Guidance, Control, and Dynamics, 2001, 24(2): 369-377.
[18] Vela P, Betser A, Malcolm J, et al. Vision-based range regulation of a leader-follower formation[J]. IEEE Transactions on Control Systems Technology, 2009, 17(2): 442-448.
[19] Panagou D, Kumar V. Cooperative Visibility Maintenance for Leader-Follower Formations in Obstacle Environments[J]. IEEE Transactions on Robotics, 2014, 30(4): 831-844.
[20] 曹志强, 张 斌. 基于行为的多移动机器人实时队形保持[J]. 高技术通讯, 2001, 11(10): 74-77.
[21] Desai J, Kumar V, Ostrowski J. Control of changes in formation for a team of mobile robots[A]. Proceedings of the IEEE International Conference on Robotics and Automation[C]. 1999, 2: 1556-1561.
[22] Balch T, Arkin R C. Behavior-based formation control for multirobot teams[J]. Transactions on Robotics and Automation, 1998, 14(6): 926-939.
[23] 刘银萍, 杨宜民. 多机器人编队控制的研究综述[J]. 控制工程, 2010, 17(9): 182-186.
[24] Goodridge S G. A fuzzy behavior-based nervous system for an autonomous mobile robot[M]. 1994.
[25] Tan K H, Lewis M A. Virtual structures for high-precision cooperative mobile robotic control[A]. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems[C]. 1996, 1: 132-139.
[26] Chen Lei, Baoli Ma. A nonlinear formation control of wheeled mobile robots with virtual structure approach[A]. Proceedings of the 34th Chinese Control Conference(CCC)[C]. 2015: 1080-1085.
[27] Jian Yuan, Tang Gongyou. Formation control for mobile multiple robots based on hierarchical virtual structures[A]. Proceedings of the 8th International Conference on Control and Automation (ICCA)[C]. 2010: 393-398.
[28] Ren W, Beard R W. Formation feedback control for multiple spacecraft via virtual structures[A]. Control Theory and Applications[C]. 2004, 151(3): 357-368.
[29] Wang L, Han Z, Lin Z, et al. A linear approach to formation control under directed and switching topologies[A]. International Conference on Robotics and Automation (ICRA)[C]. 2014: 3595-3600.
[30] Lafferriere G, Caughman J, Williams A. Graph theoretic methods in the stability of vehicle formations[A]. Proceedings of the American Control Conference[C]. 2004, 4: 3729-3734.
[31] Azuma T, Karube T. Formation control with fault-tolerance based on rigid graph theory[A]. Proceedings of SICE Annual Conference[C]. 2010:1137-1140.
[32] 王祥科, 李 迅, 郑志强. 多智能体系统编队控制相关问题研究综述[J]. 控制与决策, 2013, 28(11): 1601-1613.
[33] Kohata N, Yamaguchi T, Sato M, et al. Dynamic formation generating for intelligent transport systems using algorithm to select function by environmental information[A]. Proceedings of the IEEE/IEEJ/JSAI International Conference on Intelligent Transportation Systems[C]. 1999: 798-803.
[34] Yamaguchi T, Sato M, Kohata N, et al. Dynamic formation generating in mobile-agents using algorithm to select function by environmental information[A]. Fuzzy Systems Conference Proceedings[C]. 1999, 3: 1443-1448.
[35] 杨 丽, 曹志强, 谭 民. 不确定环境下多机器人的动态编队控制[J]. 机器人, 2010, 32(2): 283-288.
[36] Ruilei Z, Chun Y, Sheng L, et al. Hybrid dynamic formation control for nonholonomic mobile robots[A]. Proceedings of the 33rd Chinese Control Conference (CCC)[C]. 2014: 8396-8401.
[37] Li Y, Chen X. Dynamic control of multi-robot formation[A]. International Conference on Mechatronics[C]. 2005: 352-357.
[38] Li Y, Chen X. Leader-formation navigation using dynamic formation pattern[A]. Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics[C]. 2005: 1494-1499.
[39] Hou S P, Cheah C C, Slotine J. Dynamic region following formation control for a swarm of robots[A]. International Conference on Robotics and Automation[C]. 2009: 1929-1934.
[40] Ballard L, Ren W. Dynamic formation algorithms and experiments[A]. Proceedings of the 4th IEEE Conference on Industrial Electronics and Applications[C]. 2009.
[41] Low C B. A dynamic virtual structure formation control for fixed-wing UAVs[A]. Proceedings of the 9th IEEE International Conference on Control and Automation (ICCA)[C]. 2011: 627-632.
[42] Low C B, Ng Q S. A flexible virtual structure formation keeping control for fixed-wing UAVs[A]. Proceedings of the 9th IEEE International Conference on Control and Automation (ICCA)[C]. 2011: 621-626.
[43] Khatib O. Real-time obstacle avoidance for manipulators and mobile robots[J]. The international journal of robotics research, 1986, 5(1): 90-98.
[44] Song Y, Wang X, Gong Z. Safeguarded formation control via the artificial potential approach[A]. Proceedings of the 11th World Congress on Intelligent Control and Automation (WCICA)[C]. 2014: 4790-4796.
[45] Liang Y, Lee H H. Decentralized formation control and obstacle avoidance for multiple robots with nonholonomic constraints[A]. American Control Conference[C]. 2006: 6 pp.
[46] Rui P. Multi-UAV formation maneuvering control based on q-learning fuzzy controller[A]. Proceedings of the 2nd International Conference on Advanced Computer Control (ICACC)[C]. 2010, 4: 252-257.
[47] Zhao L, Ma D. Circle formation control for multi-agent systems with a leader[J]. Control Theory and Technology, 2015, 13(1): 82-88.
[48] Kowdiki K H, Barai R K, Bhattacharya S. Leader-follower formation control using artificial potential functions: A kinematic approach[A]. Proceedings of the International Conference on Advances in Engineering, Science and Management (ICAESM)[C]. 2012: 500-505.
[49] Mercado D A, Castro R, Lozano R. Quadrotors flight formation control using a leader-follower approach[A]. Proceedings of the European Control Conference (ECC)[C]. 2013: 3858-3863.
[50] Rezaee H, Abdollahi F, Menhaj M B. Model-free fuzzy leader-follower formation control of fixed wing UAVs[A]. Proceedings of the 13th Iranian Conference on Fuzzy Systems (IFSC)[C]. 2013: 1-5.
[51] Luo D, Xu W, Wu S, et al. UAV formation flight control and formation switch strategy[A]. Proceedings of the 8th International Conference on Computer Science & Education (ICCSE)[C]. 2013: 264-269.
[52] Li-Ping Y, Zong-Ji C. Decentralized formation flight control of multiple fixed-wing UAVs using only local relative states[A]. Proceedings of the 30th Chinese Control Conference (CCC)[C]. 2011: 4871-4877.
[53] Millan P, Orihuela L, Jurado I, et al. Formation control of autonomous underwater vehicles subject to communication delays[J]. IEEE Transactions on Control Systems Technology, 2014, 22(2): 770-777.
[54] Li Y P, Yan S X. Formation control of multiple autonomous underwater vehicles based on state feedback[A]. Proceedings of the 11th World Congress on Intelligent Control and Automation (WCICA)[C]. 2014: 5523-5527.
[55] Guohua D, Daqi Z, Bing S. Formation control and obstacle avoidance of multi-AUV for 3-D underwater environment[A]. Proceedings of the 33rd Chinese Control Conference (CCC)[C]. 2014: 8347-8352.
[56] Jadbabaie A, Lin J. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J]. IEEE Transactions on Automatic Control, 2003, 48(6): 988-1001.
[57] Lin Z, Broucke M, Francis B. Local control strategies for groups of mobile autonomous agents[J]. IEEE Transactions on Automatic Control, 2004, 49(4): 622-629.
[58] Ren W, Beard R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies[J]. IEEE Transactions on automatic control, 2005, 50(5): 655-661.
[59] Lin Z, Wang L, Han Z, et al. Distributed formation control of multi-agent systems using complex Laplacian[J]. IEEE Transactions on Automatic Control, 2014, 59(7): 1765-1777.
[60] Wang L, Han Z, Lin Z. Formation control of directed multi-agent networks based on complex Laplacian[A]. Proceeding of the IEEE 51st Annual Conference on Decision and Control (CDC)[C]. 2012: 5292-5297.
[61] Wang L, Han Z, Lin Z, et al. A linear approach to formation control under directed and switching topologies[A]. Proceedings of the IEEE International Conference on Robotics and Automation (ICRA)[C]. 2014: 3595-3600.
[62] Han T, Lin Z, Xu W, et al. Three-dimensional formation merging control of second-order agents under directed and switching topologies[A]. Proceedings of the 11th IEEE International Conference on Control & Automation (ICCA)[C]. 2014: 225-230.
[63] Turnbull L, Samanta B. Cloud robotics: Formation control of a multi robot system utilizing cloud infrastructure[A]. Proceedings of IEEE Southeastcon[C]. 2013: 1-4.
[64] Cook J, Hu G. Vision-based triangular formation control of mobile robots[A]. Proceedings of the 31st Chinese Control Conference (CCC)[C]. 2012: 5146-5151.
[65] Scheggi S, Morbidi F, Prattichizzo D. Human-robot formation control via visual and vibrotactile haptic feedback[J]. IEEE Transactions on Haptics, 2014, 7(4): 499-511.
[66] Wang Y, Cheng L, Hou Z G, et al. Optimal Formation of Multirobot Systems Based on a Recurrent Neural Network[J]. IEEE Transactions on Neural Networks and Learning System, 2015, PP(99):1.
[67] 张洪亮. 多机器人编队技术的研究与应用[D]. 北京:北京工业大学, 2009.
[68] Dalfior J S, Vassallo R F. Nonlinear formation control for a cooperative load pushing[A]. IEEE International Conference on Industrial Technology (ICIT)[C]. 2010: 1439-1444.
[69] Moon S, Kwak D, Kim H J. Cooperative control of differential wheeled mobile robots for box pushing problem[A]. Proceedings of the 12th International Conference on Control, Automation and Systems (ICCAS)[C]. 2012: 140-144.
[70] Bai H, Wen J T. Cooperative load transport: a formation-control perspective[J]. IEEE Transactions on Robotics, 2010, 26(4): 742-750.
[71] Eoh G, Jeon J D, Choi J S, et al. Multi-robot cooperative formation for overweight object transportation[A]. IEEE/SICE International Symposium on System Integration (SII)[C]. 2011: 726-731.
[72] Zhaohui D, Min W, Xin C. Multi-robot cooperative transportation using formation control[A]. Proceedings of the 27th Chinese Control Conference(CCC)[C]. 2008: 346-350.
[73] N. Michael, J. Fink, and V. Kumar. Cooperative manipulation and transportation with aerial robots[J]. Autonomous Robots, 2011,30(1):73-86.
[74] Lee, Taeyoung. Geometric control of multiple quadrotor UAVs transporting a cable-suspended rigid body[A]. Proceedings of the IEEE 53rd Annual Conference on Decision and Control (CDC)[C]. 2014.
[75] Farhad A.Goodarzi, Taeyoung Lee. Dynamics and Control of Quadrotor UAVs Transporting a Rigid Body Connected via Flexible Cables[A]. American Control Conference[C]. 2015: 4677-4682.
Research on Formation Control Method and Application of Multi-agent Systems
Yu Xinyi, He Yanlin, Ou Linlin, Cheng Cheng
(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)
Survey on the formation control method and application of multi-agent systems is summarized in this paper. The main problem of formation control includes three aspects: formation architecture, formation keeping and formation transformation. Firstly, a variety of formation control methods are deeply analyzed, including several methods: the leader-follower, the behavior based, the virtual structure, the graph theoretic, the dynamic formation, the artificial potential field, the learning control and so on. Secondly, the application of formation controled on multi-agent systems (mobile robots, unmanned aerial vehicles, underwater vehicles) is presented. Thirdly, the research on: the recent multi-dimensions formation control method based on complex Laplacian matrix, the other areas’ technology which is used into formation control and multiple mobile robots transportation based on multi-agent systems formation control is introduced. Finally, some unsolved problems need to be investigated in depth are proposed.
formation control; multi-agent systems; formation application
2016-12-15;
2017-02-06。
国家自然科学基金资助项目(61273116);863计划(2014AA041601-05);宁波重点项目(2014B10017);浙江省自然科学基金(LYl5F030015);浙江省公益项目(2016C31064)。
禹鑫燚(1979-),男,浙江余姚人,博士,讲师,主要从事多智能体系统协同控制和机器人路径规划与控制方向的研究。
1671-4598(2017)07-0001-07
10.16526/j.cnki.11-4762/tp.2017.07.001
TP3
A
