基于CFD的网格絮凝池内水流紊动协同效应分析

贺维鹏+曹玉烛+施周+林梦雄

摘 要 借助CFD方法对网格絮凝池内的流场进行数值模拟，并结合紊流涡旋理论和絮体多级成长模型，从水流速度分布、紊动能和紊动能耗散率等角度考察不同网格板的开孔率和间距以及过水孔洞的尺寸等条件下整个池内水流紊动的相互作用.研究发现，前述各因素对流场的影响均局限于一定的区域范围，但考虑到絮凝任何阶段水动力学环境的变化都会导致最终形成絮体性能的差异，故在实际构筑物设计时，应充分利用不同分段水流紊动间的协同效应，通过确定适宜的设计参数组合来实现絮凝效果的优化.

关键词 计算流体力学；网格絮凝池；涡旋尺寸；絮凝效果；水力优化

中图分类号 TU991.2文献标识码 A文章编号 1000-2537（2017）04-0014-07

Abstract According to turbulence vortex theory and floc multi-level growth model， turbulent interactions of water flow were explored under different perforation ratios and distances of grid plates as well as different physical dimensions of the water opening. For comparison purposes， the velocity distribution， turbulent kinetic energy and dissipation rate of turbulent kinetic energy of water flow， derived from flow-field simulations by the Computational Fluid Dynamics （CFD） method， were used. The results showed that each factor may only affect the flow field within a certain regional range of the tank. However， as the morphological characteristics of the resultant floc are highly related to the hydrodynamic environments in any part of flocculating tank， an appropriate combination of design parameters of actual structures would be determined by responsibly taking into account synergetic effects of water flow turbulence in different parts of the whole tank， in order to realize the optimization of flocculation effect.

Key words Computational Fluid Dynamics （CFD）； grid flocculating tank； vortex size； flocculation effect； hydrodynamic optimization

根據紊流涡旋理论开发的网格絮凝池，具有效率高、能耗低和占地少等优点，已被广泛应用于新建水厂或老水厂的提质改造中[1-2].其通过在构筑物内填充一定数量的扰流组件（如网格板），促使水流中形成大量的微尺度涡旋，增加颗粒间的有效碰撞率，以强化同向絮凝效果[3-5].在网格絮凝池设计时，设计者往往凭借经验从相关规范手册进行参数选取，使得极易因人为或工程个体的差异而导致实际运行效果与设计预期存在较大偏差[6].

近年来，部分学者[7-10]尝试利用计算流体力学（CFD）方法对网格絮凝池内水流结构进行数值模拟，以分析其设计参数的合理性和最优性，但多数研究只针对单个竖井，并未考虑连续串联的多格竖井内水流紊动作用的相互影响.方千里[11]虽选取絮凝池整体为考察对象，然而也仅对网格为圆形和方形时的工况进行了数值模拟.鉴于此，本文借助CFD模拟以优化絮凝效果为目标，探讨不同网格板的开孔率和间距以及过水孔洞的尺寸等条件下连续串联竖井内水流紊动的协同效应，为网格絮凝池设计参数的优选和实现其高效运行提供理论指导.

1 模型构建及模拟策略

1.1 物理模型

网格絮凝池的计算模型（图1）是按照相似准则[3]对湖南省某市级自来水厂实际构筑物缩小一定比例并予以适当简化后得到，共由5个竖井组成.其中，1#和2#位于前段，各设两层网格板；3#和4#位于中段，每个竖井设单层网格板；5#竖井位于末段，其内不设网格板.各竖井的几何尺寸详见表1.

1.2 模拟方案

根据现行设计手册中给定的参数范围[12]，拟从以下5方面依次开展CFD模拟（注：除需改变的条件外，其余结构部位的尺寸均同表1）：

（1）设置1#和2#竖井内各网格板的开孔率分别为31%，36%和45%（对应的各模型流速为0.19 m/s，0.16 m/s和0.13 m/s），以考察前段竖井各网格板的开孔率对絮凝池水流紊动特性的影响；

（2）设置3#和4#竖井内各网格板的开孔率分别为36%，45%和54%（对应的各模型流速为0.16 m/s，0.13 m/s和0.11 m/s），以考察中段竖井各网格板的开孔率对絮凝池水流紊动特性的影响；

（3）设置1#和2#竖井内两层网格板的间距分别为160 mm，190 mm和230 mm，以考察前段各竖井内网格板间距对絮凝池水流紊动特性的影响；

（4）设置1#与2#以及2#与3#竖井间方形过水孔洞的尺寸（宽×高）分别为390×120 mm，390×170 mm和390×280 mm（对应的各模型孔洞流速为0.35 m/s，0.25 m/s和0.15 m/s），以考察前段各竖井内过水孔洞尺寸对絮凝池水流紊动特性的影响；

（5）设置3#与4#以及4#与5#竖井间方形过水孔洞的尺寸（宽×高）分别为390×170 mm，390×280 mm和390×350 mm（对应的各模型孔洞流速为0.25 m/s，0.15 m/s和0.12 m/s），以考察中段各竖井内过水孔洞尺寸对絮凝池水流紊动特性的影响.

1.3 控制方程求解

选取网格絮凝池内整个液体部分为计算域，并按图1所示建立笛卡尔坐标系（z轴正向朝上）.将建立好的模型及网格导入CFD常用软件FLUENT（v6.3.26）求解器后，进行如下设置：解算器采用稳态的隐式分离法，并激活標准k-ε模型（相关参数选用默认值）；采用有限体积法求解控制方程及SIMPLE算法对压力-速度场进行解耦，对流项的离散采用二阶迎风格式，收敛残差设定为10-4.

模型入口位于1#竖井上端，采用入口流速为0.06m/s的速度进口（velocity-inlet）；出口位于5#竖井底面附近，为自由出流（outflow）；各固体壁面均采用无滑移的标准壁面（wall）边界条件.

1.4 流场紊动特性表征

（1）速度矢量图：用以直观展示絮凝池内水流速度大小和方向分布情况.

（2）紊动能k：紊流剪切力是导致絮体破碎的主要原因[13]，可直接将紊动能k作为其控制指标，且k值越大，单位质量流体紊流脉动越剧烈，微涡旋数量越多，越有利于致密性絮体的形成[5].

（3）紊动能耗散率ε：在标准k-ε模型中，紊动能耗散率ε是指微尺度涡旋紊动动能的粘性耗散率[14].可认为ε值越大，紊动能转化为热能的速度越快，絮凝池的有效能耗越高，故可将其作为絮凝效果的评价指标[3-4].

本文选用由CFD模拟获得的各竖井内距絮凝池底面不同距离处的一系列横截面（用z坐标来表示）上流体的面积加权平均紊动能k和紊动能耗散率ε的分布情况来反映水流的紊动特性及其对絮凝效果的影响.

2 结果与讨论

2.1 网格板开孔率对流场及絮凝效果的影响

图2为仅改变位于前段的1#和2#竖井内各网格板的开孔率时，网格絮凝池内水流速度大小和方向分布图.由图可知，随着前段网格板开孔率的增加，进入絮凝池的水流在经过1#和2#竖井的各网格板后其流速大小和方向变化的剧烈程度均有所减弱，但各开孔率对应的3#，4#和5#竖井内流速分布的差异性却非常小，即改变前段网格板开孔率时，其对水流速度矢量图的影响主要集中于前段，而对下游各竖井内的影响极其微弱.

同样，中段竖井各网格板的开孔率分别为36%，45%和54%时相应的水流速度矢量图的差异也主要体现在开孔率发生改变的中段竖井内，而位于絮凝池前段和末段各竖井的水流速度分布近似相同（限于篇幅，矢量图未给出）.

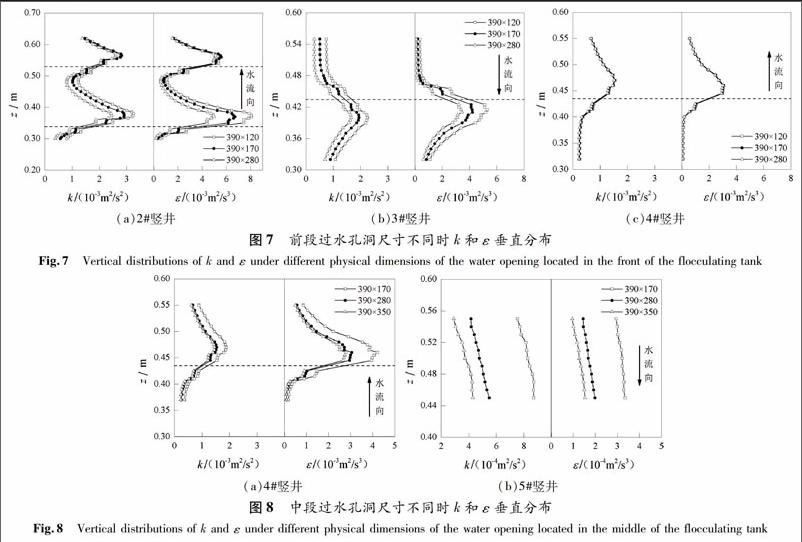
前段网格板开孔率不同时，1#，2#和3#竖井内紊动能k和紊动能耗散率ε的分布见图3.需指出的是，各分图中横虚线为网格板位置示意，同时用竖向箭头标出各竖井内的水流方向，以便于分析（下文同）.由图3a可知，在给定开孔率条件下，双层网格板对竖井内水流的紊动作用明显，如开孔率为31%时，自1#竖井上端进入絮凝池的水流，在横截面z>0.54 m上的k和ε的水平都非常低（接近于0）；当流经中心线位于横截面z=0.53 m的上层网格板后，k和ε均呈先增大后减小的变化趋势，并在横截面z=0.50 m上取得第一个极大值；继续行至横截面z=0.38 m，此时因中心线位于横截面z=0.34 m的下层网格板的阻流作用加剧了水流的扰动，k和ε又开始增大，并在通过下层网格板后的横截面z=0.30 m上取得第二个极大值.

网格板开孔率为36%和45%时，1#竖井内k和ε的垂直分布情况与开孔率为31%时的类似，只是根据孔口出流原理，水流经过具有较大开孔率的网格板后其紊动程度较弱，能量耗散率也低，因而对应于较小的k和ε（图3a）.同样，前段网格板的开孔率对2#竖井内沿水流方向的k和ε的垂直分布的影响也较大，其变化规律同1#竖井内（图3b）.然而，仅改变前段网格板的开孔率并未对位于其下游的各竖井（例如图3c的3#竖井）内的水流紊动产生太大的影响，甚至可不计.

通过对比图3a和图3b各曲线上的极大值后发现，在1#竖井各开孔率条件下以及2#竖井开孔率为31%时沿水流方向k和ε垂直分布曲线上的第二个极大值均大于第一个，并且开孔率越小，同一曲线上的极值相差越大，这可能是由于水流在到达同一竖井内下游网格板时上游网格板对其扰动的影响尚未完全消失而出现叠加导致的，并且网格板的开孔率越小，水流经过网格板的离心惯性效应越强，紊动程度和能量耗散率越高，其趋于均匀所需的流线越长（对应于较大的有效作用范围[9]），上述叠加影响越为显著.但在2#竖井内开孔率为36%和45%时，k和ε的两极值的大小却相反（图3b），其可能原因除前文所述的较大开孔率对水流的紊动作用较弱外，还因水流向上行进时部分能量用于克服重力做功而被消耗掉.

考虑到仅改变中段竖井各网格板的开孔率时，位于上游的1#和2#竖井内沿水流方向的k和ε分布受其影响可忽略，均呈现出图3中开孔率为36%条件下相应竖井内的分布情况，故现重点考察3#，4#和5#竖井内的变化规律，如图4所示.在开孔率发生改变的3#竖井内（图4a），横截面z>0.47 m的k和ε均较小且近似相等，即不同开孔率的网格板对其水流扰动的影响尚未显现；之后由于中心线位于横截面z=0.44 m的网格板上孔口出流产生的阻流作用，k和ε均呈先增大后减小的变化趋势，并在经历网格板后的横截面z=0.41 m上取得极大值，且极值大小与开孔率的关系同前；水流继续沿竖井前行，不同开孔率对应的相同截面上的k和ε的差值开始变小，造成这一现象的原因是水流行至位于其下游的井底附近时，因单层网格板有限的作用范围致使其趋于均匀流，受开孔率的影响也变得不明显.

由图4b可知，随着中段网格板开孔率的增加，4#竖井内沿水流方向的k和ε垂直分布的变化规律与3#竖井的类似，不同的是4#竖井内相同开孔率条件下k和ε的初始值和极大值均小于3#竖井的.分析其可能原因是，与3#竖井的上游竖井（即2#竖井）相比，位于4#竖井上游的3#竖井内仅布一块网格板，对水流扰动作用范围有限，再加之3#和4#竖井间的过水孔洞尺寸（390×280 mm）要大于2#和3#竖井间的（390×170 mm），对水流产生作用也较小，最终导致4#竖井内水流受上游竖井和过水孔洞的影响均小于3#竖井.此外，不同尺寸的过水孔洞对其下游竖井内水流紊动作用的影响还表现在，较小的过水孔洞在强化水流扰动的同时，还在一定程度上削弱了来水因经过位于上游的具有不同开孔率的网格板后产生的紊动特性的差异，从而导致在相同数量级（10-4）时，不同中段网格板开孔率条件下5#竖井内k和ε垂直分布受上游网格板开孔率的影响（图4c）略大于不同前段网格板开孔率条件下3#竖井内的（图3c）.

综上，网格板开孔率对絮凝池内流场的影响，主要体现在开孔率发生改变的竖井内，且在网格板下游附近区域尤为显著，而对位于上游和下游的其他竖井内水流分布的影响较为微弱.结合紊流涡旋理论[3]和絮体多级成长思想[13]可知，网格絮凝池任何分段的水流紊动特性的差异均会导致本段各竖井所形成絮体在形态上各异，最终影响到絮凝末期絮体的质量以及固液分离效果.因而，在选择各段竖井内网格板的数量及相应的开孔率时，应考虑不同分段水流紊动间的协同效应，通过确定适宜的设计参数组合来实现絮凝效果的优化.

2.2 网格板间距对流场及絮凝效果的影响

由2.1节的分析可推知，若能合理利用同一竖井内上游网格板的有效作用范围，就可显著提高水流经过下游网格板后的紊动效果，加大微尺度涡旋的比例，提高颗粒的有效碰撞所需能耗，以促进高性能絮体的快速形成.武道吉等[5]通过理论推导提出，对絮凝最有效的涡旋应为尺度接近且略大于絮体颗粒的，而尺度小于絮体粒度的涡旋不仅难以推动悬浮颗粒作变速运动，同时还会增加对已形成絮体的冲击破碎作用.基于此，笔者认为，在进行网格板间距的设计时，最为理想的方案是应将下游网格板设置于与其紧邻的上游网格板的有效作用范围内且最好位于上游网格板已形成的与絮体粒度相近的涡旋完全或绝大多数消失的临界位置.这样做的优势在于，下游网格板既不会破坏上游网格板产生的对絮凝有利的涡旋，同时还可将上游网格板形成的不利于絮体成长且尚未消失的涡旋中携带的能量转移至下游网格板形成的涡旋中，通过能量叠加来实现其最大化的有效利用.接下来将探讨在网格板开孔率和其他条件均相同的前提下，前段各竖井内网格板间距对絮凝池内水流分布及絮凝效果的影响.

与仅改变前段竖井中各网格板开孔率的情况类似，网格板间距分别为160 mm，190 mm和230 mm时相应的水流速度矢量图的差异主要体现在位于前段的1#和2#竖井内，而各间距对应的3#，4#和5#竖井的流速分布近似相同.并且，间距越小，1#和2#竖井内上游网格板对下游网格板在水流扰动上的叠加作用越显著，两板间流速的分布也越不规则（限于篇幅，相关矢量图未给出）.

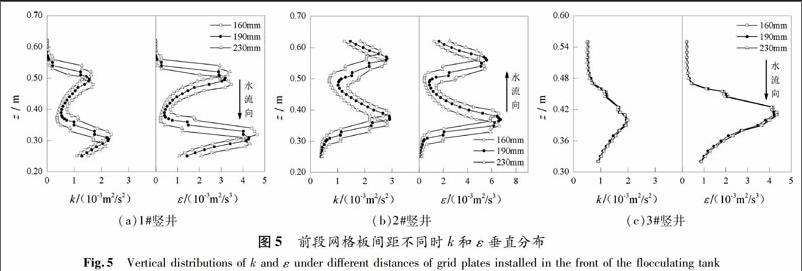
图5为前段网格板间距改变时，1#，2#和3#竖井内紊动能k和紊动能耗散率ε的分布图.由图5a可知，1#竖井的k和ε分布曲线上沿水流方向依次出现的两个极值的大小和横截面位置，均与网格板间距密切相关.具体而言，较小间距（如160 mm）时，水流通过上游网格板产生的绝大多数能量尚未耗散完全就已受到下游网格板的影响，虽然此时两层网格板间涡旋中携带的能量可迁移至下游网格板形成的涡旋中，但部分对絮凝有利的涡旋可能在转运过程中遭受破坏，势必造成能量损失，影响絮体成长；间距增至190 mm时，水流行至横截面z=0.39 m的位置，上游网格板输入的能量仅剩少部分未被粘性耗散，即可认为接近于该网格板有效作用范围的边界，此后下游网格板的影响开始凸现，再次加剧对水流的扰动，同时两板间尚未消散涡旋携带的能量还可被迁移至下游网格板形成的涡旋中，从而在整个竖井内形成有利于絮体成长的紊动环境，实现能量的高效利用；间距继续增至230 mm时，k和ε分布曲线上两极值的差值均小于其他间距的，即上游网格板对下游网格板水流扰动的叠加影响开始减弱，此时1#竖井内两网格板的作用变得相对独立，不能满足前文提出的最为理想的间距方案.

同样，前段网格板间距对2#竖井内沿水流方向的k和ε垂直分布的影响也较大，其变化规律同1#竖井内的（图5b），但对位于其下游各竖井（例如图5c的3#竖井）内的水流紊动特征的影响很微弱.

2.3 过水孔洞尺寸对流场及絮凝效果的影响

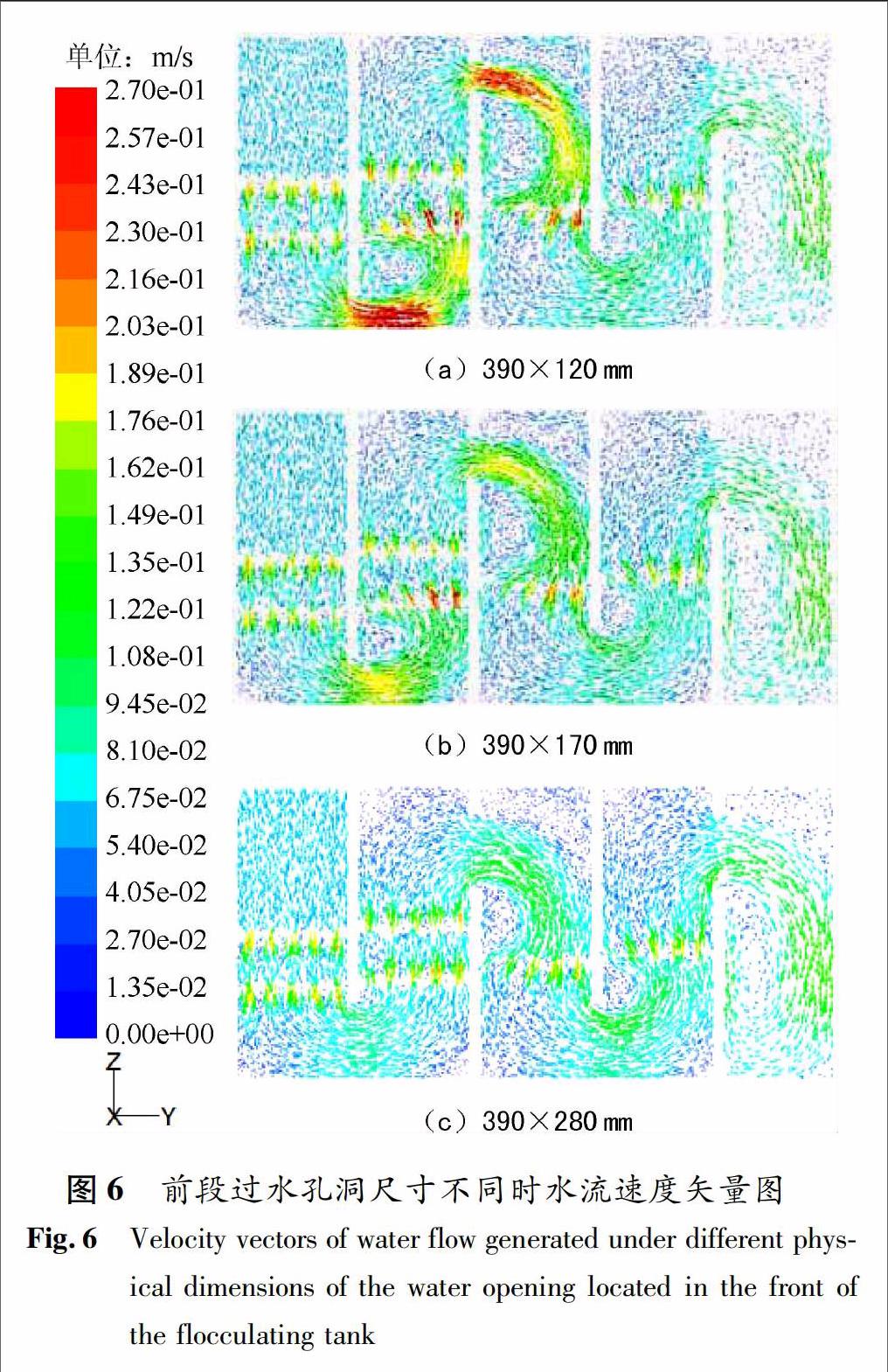
图6为仅改变1#与2#以及2#与3#竖井间过水孔洞的尺寸（宽×高）时，网格絮凝池内水流速度大小和方向分布圖.由图可知，随着前段过水孔洞高的增大，流体经过这些孔洞时流速不均匀分配程度均有所减弱，同时在由孔洞边壁约束形成的“U型流”转弯处流速明显减小，进而对紧邻其下游的2#和3#竖井内沿水流方向上游一定范围的流速分布产生显著影响，但对1#，4#和5#竖井内的影响都较小.同样，中段方形过水孔洞的尺寸分别为390×170 mm，390×280 mm和390×350 mm时相应的水流速度矢量图的差异也主要体现在紧邻尺寸发生改变的过水孔洞下游的4#和5#竖井内，而在1#，2#和3#竖井内相应的水流速度分布近似相同（限于篇幅，矢量图未给出）.

前段过水孔洞的尺寸发生改变时，1#竖井内各尺寸对应的紊动能k和紊动能耗散率ε的分布曲线的形状，均与图3a中前段网格板开孔率为36%时的相同；同样，仅改变中段过水孔洞的尺寸时，位于这些孔洞上游的1#，2#和3#各竖井内不同尺寸对应的k和ε分布曲线也均几乎重合，即类似于流速分布，不同尺寸的过水孔洞对位于其上游竖井的k和ε垂直分布的影响都很小，故对此不予讨论.现重点考察前段和中段过水孔洞尺寸改变时位于其下游各竖井内k和ε分布的变化规律，如图7和图8所示.

水流自1#竖井经不同尺寸的过水孔洞流入2#竖井后，在2#竖井内沿水流方向的各横截面上k和ε的分布各异（图7a），表现为在位于其上游的横截面z<0.32 m范围内，不同尺寸对应的k和ε都存在较小的差异，且较大尺寸的孔洞对应着较小的指标值；当水流经过中心线位于横截面z=0.34 m的上游网格板后，因孔口出流的作用导致上述差异被放大；水流继续行至中心线位于横截面z=0.53 m的下游网格板附近，不同尺寸对应的k和ε的差值开始变小，并在通过下游网格板后的横截面z=0.57 m时，k和ε的分布曲线均趋向重合，也即前段过水孔洞尺寸的改变仅对2#竖井内沿水流方向一定范围的k和ε分布有较大的影响.

与2#竖井内的分布略微不同，2#与3#竖井间过水孔洞尺寸的改变会对位于其下游的3#竖井内沿水流方向的各横截面上的k和ε均产生影响（图7b）.造成这种差别的可能原因是，不同于以下向流为主流的3#竖井，2#竖井内水流自下而上运动时，在惯性力的驱使下不仅要克服重力做功，同时还要抵抗双层网格板上孔口出流的阻流作用，均在一定程度上削弱了上游过水孔洞尺寸的影响.仅改变中段过水孔洞尺寸时（图8），4#与5#竖井内各自对应的k和ε的垂直分布的变化规律可再次佐证这一分析，只是以上向流为主流的4#竖井内网格板数量（图8a）少于同为上向流的2#竖井内的（图7a），此条件下对上游过水孔洞尺寸影响的削弱作用较小.由图7还可知，前段过水孔洞尺寸的改变仅对以尺寸发生变化的孔洞为进水口的竖井内k和ε分布产生较大影响，而对位于其下游的其他竖井（例如图7c的4#竖井）内的水流紊动特征的影响却非常微弱.

上述分析表明，过水孔洞在完成相邻竖井间水流输送任务的同时，还会对紧邻其下游的竖井内水流速度分布和紊动特征产生影响，且尺寸越小，作用越显著，同时当水流通过竖井内网格板后，在惯性效应的作用下相关影响将被进一步放大，存在协同作用关系，最终导致絮体形成过程及絮凝效果的差异.因而在实际设计中，对絮凝池各分段相邻竖井间过水孔洞尺寸的合理确定也非常关键，应将其放在与网格板设计同等重要的地位.

3 结论

（1）网格板的开孔率和间距对絮凝池内水流速度分布和紊动特性的影响，主要体现在网格板结构变化的竖井内，而过水孔洞尺寸的影响主要表现在以尺寸发生改变的孔洞为进水口的竖井内.

（2）不同尺寸过水孔洞对流场的影响会在紧邻其下游竖井内网格板的作用下得以放大，同时较小的过水孔洞还可削弱来水因经过位于上游的具有不同结构特征的网格板后产生的紊动特性的差异.

（3）根据絮体多级成长思想，任何竖井内水动力学环境差异均会导致本竖井以及位于其下游各竖井内不同的絮体形成过程，最终影响絮凝末期絮体的形态和质量.

（4）在网格絮凝池设计时，不仅要从整体上把控池内水动力学条件的平均水平符合相关规范要求，还应特别注意不同分段或竖井内水流紊动间的协同效应，以便确定适宜的设计参数组合来实现絮凝效果的优化.

参考文献：

[1] 汪义强，陈 超. 水力絮凝池发展与展望[J]. 净水技术， 2005，24（1）：36-39.

[2] 游晓宏，陈晓琼. 混凝技术及其发展[J]. 工业水处理， 2002，22（11）：7-9.

[3] 王紹文. 惯性效应在絮凝中的动力学作用[J]. 中国给水排水， 1998，14（2）：13-16.

[4] WATANABE Y. Flocculation and Me[J]. Water Research， 2017，114：88-103.

[5] 武道吉，谭风训，王江清. 紊流絮凝技术研究[J]. 水处理技术， 1999，25（3）：171-173.

[6] 王冬敏，王艳丽. 网格絮凝池的发展及研究展望[J]. 广东化工， 2016，43（17）：79.

[7] 李国强，邴 帅，刘鹏亮，等. 基于CFD的网格絮凝池栅间距特性研究[J]. 城市道桥与防洪， 2014（11）：193-195.

[8] 易中慎. 基于CFD的网格絮凝池参数优化设计研究[J]. 内蒙古科技与经济， 2016（7）：117-119.

[9] 仲崇军. 基于CFD的水处理网格絮凝池优化设计研究[D]. 武汉：华中科技大学， 2009.

[10] 赵 琦. 微涡旋网格絮凝池特性参数的数值模拟与过程优化[D]. 哈尔滨：哈尔滨理工大学， 2016.

[11] 方千里. 圆形网格孔眼对网格絮凝池絮凝水力条件的影响研究[D]. 合肥：合肥工业大学， 2016.

[12] 上海市政工程设计研究院. 给水排水设计手册（第3册）： 城镇给水[M]. 2版. 北京： 中国建筑工业出版社， 2004.

[13] HE W， NAN J， LI H， et al. Characteristic analysis on temporal evolution of floc size and structure in low-shear flow[J]. Water Research， 2012，46（2）：509-520.

[14] 王福军. 计算流体动力学分析：CFD软件原理与应用[M]. 北京： 清华大学出版社， 2004.