单侧限位悬臂梁碰撞系统的动力学实验研究∗
2017-08-28朱媛张磊宋汉文
朱媛 张磊 宋汉文
(同济大学航空航天与力学学院,上海 200092)
单侧限位悬臂梁碰撞系统的动力学实验研究∗
朱媛 张磊 宋汉文†
(同济大学航空航天与力学学院,上海 200092)
对构造的单边碰撞悬臂梁系统进行实验的定性研究,在基础激励实验中,变换多次激励频率,通过加速度传感器测量悬臂梁测点的响应信号,并通过力传感器测量得到限位器与柔性悬臂梁之间的碰撞力.通过Matlab软件对实测响应的时、频域分析处理,观察到系统复杂的周期、概周期、混沌等多种运动形式,并发现其中运动形式变化的区间存在突变.尝试对实验时域数据计算最大Lyapunov指数,以进一步验证其中混沌的存在,进一步发现了混沌响应下末端加速度响应与碰撞力的传递函数具有频响函数特征.实验研究体现了非线性动力学现象,也对分析应用混沌运动的实验结果提供了一个新视角.
非线性振动, 悬臂梁, 单边碰撞, 周期运动, 混沌运动
引言
在实际工程系统运转工作中,机械系统内某个零部件之间或者零部件与边界间发生碰撞冲击是十分常见的,例如蒸汽涡轮发动机中换热管与支撑板的碰撞振动,航天器伸展系统关节处间隙导致碰撞的发生,这类碰撞运动一般由多参数控制,而且具有不连续突变性和强非线性,一方面会造成机械部件的疲劳损伤,在文献[1]中列举了许多具有实际应用意义的研究实例,另一方面也会造成系统控制运转的误差.为了优化设计这类碰撞机械系统,对其碰撞的动力学行为的全面了解就格外重要.因而上世纪80年代起国内外学者就开始将其作为一种重要的物理系统进行研究,为进一步采用理论建模和数值仿真来构建不同的碰撞模型,设计实验并来观察验证其中蕴含的丰富复杂的动力学特性显得格外重要.Moon和Shaw[2]通过调整基础正弦激励幅值和频率等参数,在柔性梁末端置放限位器碰撞模型中观察到非周期或混沌的运动形式,Thompson和Bishop[3]同样建立悬臂梁末端限位器的碰撞模型,测量运动响应的同时用力传感器测得碰撞力,调整激励频率,并对实验结果绘制相图和响应功率谱分析,通过分岔图的分析观察到了单周期到混沌的分岔过程,Thompson[4]还从实验中观察到了倍周期分岔现象.Wiercigroch[5]等设计对单一质量块上下安装柔性梁作为碰撞发生的限位器,通过调整限位器与质量块的间隙,外激励幅值等参数得到不同的周期谐波碰撞,次谐波碰撞和混沌运动,并在文献[6]中对实验数据做功率谱分析并观察到了混沌现象.Piiroinen[7]研究了钟摆碰撞实验模型,观察到了其中的多周期运动形式和擦边分岔.Hinrich[8]对传送带上集中质量块的摩擦碰撞现象进行实验研究,Virgin[9]则以带有凹形轨道上的小球为实验对象,研究其在运动中与轨道挡板上的碰撞运动形 式.Blazejczyk-Okolewska 和 Peterka[10,11]发现在碰撞过程中出现的混沌吸引子的突变和间断,Chin W和Nordmark[12-14]分析得到了不同形式的擦边分岔.金栋平[15]等设计了两柔性梁碰撞实验来研究碰撞振动类型,在实验中观察到亚谐、超谐、概周期、混沌以及谐碰撞与混沌共存的运动类型,还发现类似“频率锁定”的碰撞振动,曹妍妍[16]根据航天器内部设备的间隙减振机构设计实验模型,得到各种不同的周期混沌状态.
本文的研究对象是带有单侧限位器悬臂梁碰撞系统,继承文献[17]中的工作,在实验中对设计的模型系统施加基础正弦激励,采集碰撞力以及悬臂梁末端加速度时域信号.重点观察分析悬臂梁在运动过程中与限位器不断发生碰撞,整个系统表现出强非线性现象.通过绘制悬臂梁测点的时域响应以及相图和庞加莱截面可以发现其丰富的动力学行为,分析对比各种不同的周期和混沌响应形式,并通过对响应的时域数据相空间重构计算李雅普诺夫来验证混沌的存在.进一步对周期运动和混沌形式的实验响应分别做加速度信号的频率功率谱分析,发现各自能量的不同分布特点.并通过分别计算周期运动和混沌运动实验数据的相干函数和传递函数等发现其不同特征.
1 实验系统
1.1 实验模型
为了得到更好的实验现象,本文设计了如图1的简化悬臂梁碰撞系统,选用质量60g的轻质均匀弹性不锈钢梁,杨氏模量209Gpa,几何尺寸通过实际测量得长280mm,宽30mm,厚度1mm.实验开始前将梁的上端由夹具螺栓固定在竖板上部,竖板底部与基础通过螺栓相连,悬臂梁可以在水平基础激励方向自由运动,为记录其运动情况,在其末端处左右对称位置分别附有质量为0.95g的加速度传感器,同时作为悬臂梁末端的集中质量考虑.
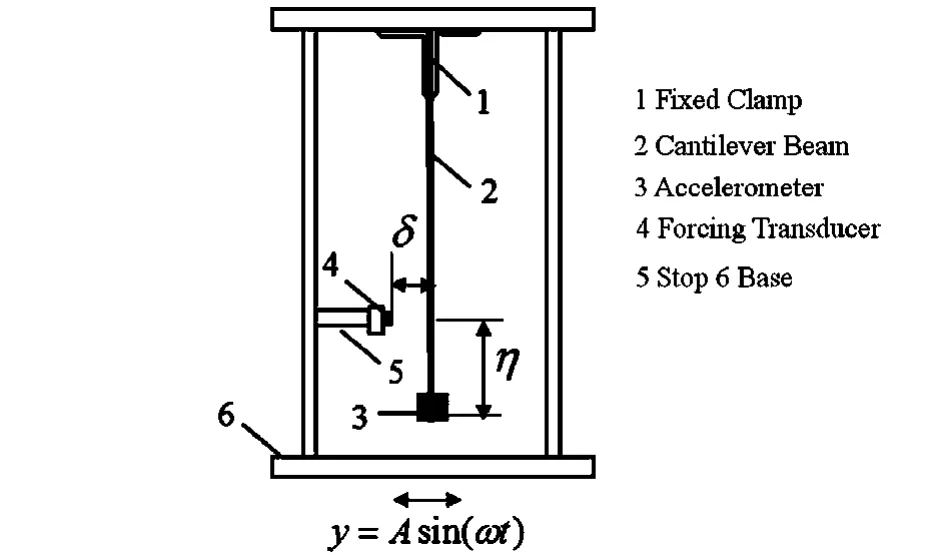
图1 实验模型Fig.1 Experimentalmodel
实验中通过激振器对模型整体施加水平正弦定频激励y=Asin(ωt),其中A为基础位移幅值,ω为激励频率.模型可以通过限位器装置调整改变悬臂梁碰撞点位置η和限位器与碰撞点水平间隙δ的大小.边菁[18]通过对双边限位悬臂梁进行动力学实验,分析了碰撞点位置,激励频率,限位器间隙宽度等对实验现象的影响.为重点研究不同外激励频率下系统响应的特征,实验中选择将图1中限位器与悬臂梁碰撞点的间隙δ取为零的临界情况.这样在实验过程中悬臂梁每次运动到平衡位置处都会与限位器发生碰撞,从而使简单的线性悬臂梁系统成为本构非线性模型.另外实验借鉴了Thompson[11]做法,在限位器端部通过安装Kistler力传感器与悬臂梁发生碰撞,为了加强碰撞作用,实验选用钢制头,用力传感器测量记录了每次碰撞发生限位器与柔性梁之间的碰撞力,通过对碰撞力时域和频域的分析可以更好地认识理解碰撞发生的运动过程和规律.
1.2 实验方案及步骤
为了更准确地测量实验数据,我们设计了如图2的实验流程,本次实验测试设备主要有电磁式振动台(Labworks Model ET-139)、功率放大器(Labworks Model PA-141)、振动控制器(M+P振动控制(VXICT-100C))、加速度传感器(上海标智14026型IEPE传感器)和力传感器(Kistler 9712B500).

图2 实验流程Fig.2 Experiment flowchart
在实验中选择使用M+P振动控制设备给激振器提供正弦激励信号.M+P振动控制器通过实时采集在水平滑台侧方安装的加速度传感器信号,并将其与激励信号比较进行反馈从而实现加速度恒幅控制.具体实验操作包括以下两部分:
(1)通过锤击法对无碰撞发生的带有集中质量的悬臂梁模型进行模态实验.实验中保证悬臂梁上端与竖板通过夹具紧密固定边界条件不变,同时选择之后正弦激励实验中悬臂梁发生碰撞的位置处作为锤击位置,得到系统前4阶模态参数;
(2)在距离悬臂梁末端η=6cm高度处固定安装限位器,对模型整体进行定频正弦振动实验.实验中控制振动台激励的幅值为2m/s2,激励频率从3Hz到150Hz变化,频率间隔为1Hz,总共有148个单次实验,这其中包括了无碰撞悬臂梁模型的前三阶固有频率:6Hz,46Hz,140Hz.另外,为保证得到每个激励频率作用时模型稳态时的非线性响应,排除掉瞬态响应的影响,每个单次实验记录120s.由于本次实验中碰撞时间非常短且发生密集,为了充分捕捉到完整的碰撞信号,采集过程中将采样频率取为2048Hz.
同时要注意的是实验模型中的悬臂梁上部与夹具用两排螺栓固定,以减小实验过程中强烈碰撞造成的位移误差[16],并保证全部实验过程中边界条件不变.
2 实验结果
2.1 无碰撞发生的悬臂梁模态实验结果
在无碰撞发生时,悬臂梁模型为线性系统,通过模态实验得到的前4阶固有频率和阻尼比如表1所示,同时表1中我们也列出将实际物理参数代入等截面梁横向弯曲自由振动的运动微分方程得到的悬臂梁固有频率理论值,对比发现理论值和实验值在前3阶有非常好的对应,第4阶固有频率的误差虽然相较前3阶的误差较大,但总体说来其相对误差(约2%)比较小,说明实验结果的可靠.

表1 带集中质量悬臂梁系统模态参数Table 1 Modal parameters of the cantilever beam system with lumped mass
2.2 碰撞发生悬臂梁系统动力学行为分析
受篇幅限制,这里仅选取几个实验振动响应结果中比较有代表性的几组列出,并将记录加速度时域信号进行积分计算得到位移和速度响应,从而通过庞加莱映射、谱分析等时域频域分析处理,观察总结到一些现象和规律.
首先发现在实验碰撞结果中出现了多种周期运动形式,区别于非碰撞悬臂梁系统的第一阶固有频率6Hz,发现在11Hz及其倍频上响应均为周期形式.为了方便识别周期特征,对时间轴作归一化处理,即 t/Tf,其中 Tf为外激励周期.用 k=p/n 定义周期运动特征,p表示限位器与悬臂梁发生碰撞的次数,n表示外激励周期数.首先观察到在外激励频率为11Hz时,如图3(a)中分别用红色和蓝色曲线代表悬臂梁末端和振动台的位移时域响应,图(b)记录了每次碰撞发生时力传感器的测量时域数据,由此观察到在每个外激励周期发生一次碰撞,取时间历程60s到120s稳态响应,绘制相图(c),同时按每相邻整数倍个外激励周期Tf(Tf=2π/ω)观察时程曲线得到庞加莱截面,如图(d)所示,系统作单周期运动,可记为1/1.同理发现在11Hz倍频附近22Hz,34Hz,45Hz处有不同形式的周期运动,如图4,5,6所示,各自运动响应形式分别记为 1/2,1/3,1/4.除此之外,实验中也发现了在悬臂梁末端一个周期运动中碰撞两次的形式,如图7,8,9 所示,分别为外激励频率在 12Hz,33Hz,48Hz 的结果,可分别记为 2/2,2/6,2/8.另外在11Hz及其倍频处,悬臂梁集中质量的运动位移和速度响应相比各自附近其他频率下的运动响应明显增大,这类似于线性系统中在外激励频率等于系统模态频率出现的“共振”现象.可以理解11Hz为该非线性系统本身具有的一个特殊规律频率.然而另一方面随着基础频率的增大,这一规律变得不再明显,猜想这可能是混入了系统的更高阶响应.

图3 11Hz实验结果(a)悬臂梁末端位移时域响应;(b)碰撞力;(c)相图;(d)庞加莱截面Fig.3 Experimental results for 11Hz(a) Time-domain displacement response of the free end of the beam;(b) Impact force; (c) Phase figure; (d) Poincare section

图4 22Hz实验结果(a)悬臂梁末端位移时域响应;(b)碰撞力;(c)相图;(d)庞加莱截面Fig.4 Experimental results for 22Hz(a)Time-domain displacement response of the free end of the beam;(b)Impact force; (c) Phase figure; (d) Poincare section
我们也发现该非线性系统随激励频率变化出现的不同运动响应之间存在突变,如图10所示分别为 19Hz,20Hz,21Hz,23Hz 激励下响应的相图,对比图4(c)中22Hz的相图,可以发现这期间拓扑结构发生了突变,且有通往混沌的可能.这证明非线性系统中对于基础激励频率的参数变化十分敏感,但遗憾的是实验中基础激励频率变化的分辨率为1Hz,未能观察到关于突变更为细致的变化形式.

图5 34Hz实验结果(a)悬臂梁末端位移时域响应;(b)碰撞力Fig.5 34Hz Experimental results(a)Displacement time response of the free end of the beam;(b)Impacting force

图6 45Hz实验结果(a)悬臂梁末端位移时域响应;(b)碰撞力Fig.6 Experimental results for 45Hz(a) Time-domain displacement response of the free end of the beam;(b) Impact force

图7 12Hz实验结果(a)悬臂梁末端位移时域响应;(b)碰撞力Fig.7 Experimental results for 12Hz(a)Time-domain displacement response of the free end of the beam;(b)Impact force

图8 33Hz实验结果(a)悬臂梁末端位移时域响应;(b)碰撞力Fig.8 Experimental results for 33Hz(a)Time-domain displacement response of the free end of the beam;(b)Impact force

图9 48Hz实验结果(a)悬臂梁末端位移时域响应 (b)碰撞力Fig.9 Experimental results for 48Hz(a) Time-domain displacement response of the free end of the beam;(b) Impact force

图10 不同外激励实验结果比较(a)19Hz实验结果相图;(b)20Hz实验结果相图;(c)21Hz实验结果相图;(d)23Hz实验结果相图Fig.10 Comparison of different experimental results(a) Phase figure for 19Hz;(b) Phase figure for 20Hz;(c) Phase figure for 21Hz;(d) Phase figure for 23Hz
另外我们在实验结果中也发现了在一些外激励频率下出现的概周期响应形式,如图11,12所示,外激励分别为100Hz,111Hz的悬臂梁末端位移和相图,可以发现在时间位移历程图中有明显的包络线.

图11 悬臂梁末端位移时域响应(a) 100Hz; (b) 111HzFig.11 Time-domain displacement response of the free end of the beam(a) 100Hz;(b) 111Hz

图12 相图 (a)100Hz;(b) 111HzFig.12 Phase figure for(a) 100Hz and (b) 111Hz
此外,我们选取外激励频率等于无限位器悬臂梁第一阶模态固有频率6Hz和74Hz的情况,图3-13(a),3-14(a)分别为两种情况下悬臂梁末端加速度、碰撞力以及控制振动台的正弦激励幅值时间历程图,这里仅取2s时段,观察到在周期正弦激励下系统响应呈现非周期性.随着碰撞的发生,测到碰撞力的同时发现悬臂梁末端加速度系统响应发生突变,进一步绘制相图,如图 3-13(b),3-14(b),庞加莱截面如图 3-13(c),3-14(c),形成了一些成片的密集点,可以初步验证混沌的存在.
之后我们考察不同响应形式在频域中的能量分布情况,首先对周期运动的悬臂梁末端加速度响应和碰撞力时域数据做功率谱密度分析,以11Hz,22Hz为例结果如图15,每个激励倍频上都有竖直的细高峰,使得整体功率谱谱线成梳状形状.图中竖直的红色虚线同样标注了无限位器悬臂梁的高阶模态所在频率,在这些相应频率对应处加速度功率谱中没有出现明显的峰值,力功率谱中也没有相应谷值.

图13 6Hz实验结果(a)悬臂梁末端加速度,碰撞力,激励时域数据;(b)相图; (c)庞加莱截面Fig.13 Experimental results for 6Hz(a)Time-domain acceleration response of the free end of the beam,impact force and base excitation; (b)Phase figure; (c)Poincare section
进一步分别对图13,14中混沌响应的末端加速度和碰撞力作功率谱分析,发现功率谱密度曲线有宽谱特征.如图 16所示,图(a),(b)分别为外激励频率6Hz和74Hz的结果,从图中发现由于碰撞的发生在低频激励的响应中出现了高频成分,更多频率成分开始参与到运动中,图中竖向虚线部分标注的 ω2,ω3,ω4分别为无限位器悬臂梁的第二、三、四阶固有频率,可以看出两组加速度功率谱谱线在这些地方有类似频响曲线特征出现的峰值,而在力的功率谱图中这些地方则出现谷值.另外二者在激励频率的倍频和分数频上幅值明显较大,证明在这些频率上能量分布较多,但第二阶模态频率之后这种特征不再明显.

图14 74Hz实验结果(a)悬臂梁末端加速度,碰撞力,激励时域数据;(b)相图; (c)庞加莱截面Fig.14 Experimental results for 74Hz(a)Time-domain acceleration response of the free end of the beam,impact force and base excitation;(b)Phase figure;(c)Poincare section

图15 功率谱结果11Hz加速度功率谱(上)力功率谱(下)Fig.15 Power spectrum results(top) Acceleration power spectrum for 11Hz;(bottom) Impact force power spectrum

图16 功率谱结果(a)6Hz加速度功率谱(上)力功率谱(下);(b)74Hz加速度功率谱(上)力功率谱(下)Fig.16 Power spectrum results(a) (top) acceleration power spectrum for 6Hz,(bottom) impact force power spectrum;(b)(top) acceleration power spectrum for 74Hz,(bottom) impact force power spectrum
2.3 碰撞实验数据李雅普诺夫指数计算
在非线性动力系统的研究中,目前判定其运动特性最精确的一种工具是Lyapunov指数谱,它是判断混沌系统最可靠的一种定量方法.它给出了系统任意相邻相轨线平均发散程度或平均收敛程度的一种度量[19].为了进一步验证本实验中出现的混沌响应,本文也对这一指数作了简单的考量.
对于非线性系统是否存在动力学混沌,往往不需要计算出所有的Lyapunov指数,可以从最大Lyapunov指数是否大于零而非常直观地判断出来:一个正的Lyapunov指数,意味着在系统相空间中,无论初始两条轨线的间距多么小,其差别都会随着时间的演化而成指数率的增加以致达到无法预测,这就是混沌现象[20].目前常用的计算混沌序列最大Lyapunov指数的方法以Wolf方法和小数据量方法应用最为广泛,也最为实用.通过对时间序列重构相空间,本文分别采用以上两种方法对实验中部分周期运动(11,33Hz)和混沌运动(6,74Hz)时间序列分别计算了最大Lyapunov指数,考虑到混沌运动状态对初始条件的敏感度,本文保证每次实验在悬臂梁竖直静止于平衡位置处开始施加外激励,之后对比由相同零初始条件实验下的计算结果如表2所示。

表2 李雅普诺夫指数计算结果Table 2 Results of Lyapunov exponent
可以发现两种方法虽然在计算结果上有所不同,但对于周期和混沌运动形式上定性的判定是一致的,即在6Hz和74Hz下出现的响应形式具有混沌特征.
2.4 实验数据传递函数和相干函数比较
通过实验测得的末端加速度响应与碰撞力响应做传递函数,结果如图17所示,图中用红色曲线标注了模态实验得到的前4阶固有频率对应频率.可以发现在周期响应下11Hz得到的传递函数毛刺十分多,而且激励倍频特征十分明显,而混沌响应6Hz的传递函数则十分光滑,而且包含准确的模态频率信息,具有模态实验中频响函数的特征,这为从混沌响应中辨识原始模态参数提供可能.

图17 实验传递函数(a) 11Hz传递函数; (b) 6Hz传递函数Fig.17 Coherence function(a) Transfer function for11Hz; (b) Transfer function for 6 Hz
在模态分析中,可以采用相干函数来检验传递函数的有效性.相干函数是一个在频域上描述两过程相关特性的函数,表示系统输入与输出的因果程度,其表达式为:

式中,GFY表示输入与输出的互功率谱密度函数,GFF表示输入的自功率谱密度函数,GYY表示输出的自功率谱密度函数.若在某个频率上相干函数为0,说明响应与激励在此频率上不相关.相反,如果相干函数为1,说明完全相关.
由于本实验中测量到了每次碰撞发生时碰撞力的大小,可以将碰撞力视为对悬臂梁系统的输入,将悬臂梁末端加速度作为输出,这样通过计算得到不同响应形式下的相干函数来考量碰撞力与悬臂梁末端响应的因果程度.我们对比之前周期(激励为11Hz)和混沌(激励为6Hz)响应下的相干函数结果分别如下图18所示.可以看到图18(b)中的大部分频率上,相干函数趋近于1,说明碰撞力信号与响应信号因果性较好.相干函数接近于0的频率,除去在激励频率位置,主要分布在传递函数的峰值上(无碰撞系统的固有频率)、谷值上(传递函数的反共振点),这分别是由于傅里叶变换过程中的泄露现象和系统在反共振点上信噪比较低,而相比于图18(a)中的周期运动的相干函数并不理想.
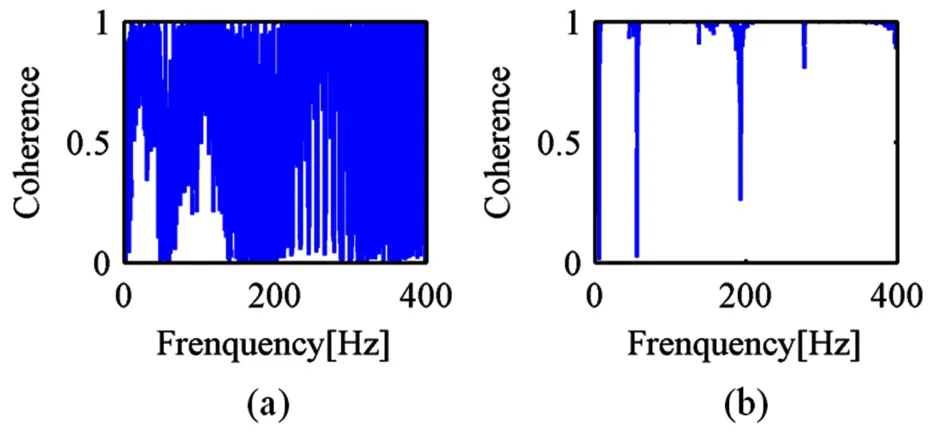
图18 相干函数(a)11Hz相干函数;(b)6Hz相干函数Fig.18 Coherence function(a) Coherence function for 11Hz(b) Coherence function for 6 Hz
3 结论
通过对单侧限位器悬臂梁碰撞模型进行了一系列固定幅值、不同频率下的基础正弦激励实验,发现其中蕴含了丰富的碰撞响应特征,具有复杂的非线性行为.
(1) 在激励频率为 11Hz,12Hz,22Hz,33Hz,34Hz,45Hz,48Hz等11倍频及其附近的实验结果中发现多种周期运动形式和碰撞规律,包括1/1,2/2,1/2,2/6,1/3,1/4,2/8 等,且在 11Hz 倍频激励下的运动响应结果较其他情况下响应较大,从而认为11Hz在本文非线性模型中为一个特殊规律特征频率.
(2)在激励频率100Hz,111Hz等情况下出现概周期运动形式,而且在实验条件下发现周期、概周期、混沌等形式之间随激励频率变化发生突变.
(3)对于6Hz,74Hz等激励频响下会出现的混沌响应,通过计算最大李雅普指数作为判据,并与周期运动下最大李雅普指数结果对比,定性上得到很好的一致性结论.
(4)利用实验所测的悬臂梁末端加速度响应与碰撞力做传递函数,分别绘制比较实验数据中周期运动和混沌运动下碰撞力信号与悬臂梁末端加速度响应的相干函数,发现混沌响应下的传递函数与模态试验的频响函数有相似特征,为分析利用混沌响应实验数据提供了新角度.
1 Jerrelind J,Stensson A.Nonlinear dynamics of parts in engineering systems.Chaos Solitons & Fractals, 2000,11(15):2413~2428
2 Moon F C,Shaw S W.Chaotic vibrations of a beam with non-linear boundary conditions.International Journal of Non-Linear Mechanics, 1983,18(6):465~477
3 Bishop S R,Thompson M G,Foale S.Prediction of period-1 impacts in a driven beam.In:Proceedings of the Royal Society of London.Series A:Mathematical.Physical and Engineering Sciences, 1996,452(1954):2579~2592
4 Thompson M G,Bokaian J M T,Ghaffari A R R.Subharmonic resonances and chaotic motions of a bilinear oscillator.IMA Journal of Applied Mathematics, 1983,31(3):207~234
5 Wiercigroch M,Sin V W T.Experimental study of a symmetrical piecewise base-excited oscillator.Journal of Applied Mechanics, 1998,65(3):657~663
6 Wiercigroch M,Sin V M T,Li K.Measurement of chaotic vibration in symmetrically piecewise linear oscillator.Chaos Solitons& Fractals, 1998, 9(1):209~220
7 Piiroinen P T,Virgin L N,Champneys A R.Chaos and period-adding:Experimental and numerical verification of the grazing bifurcation.Journal of Nonlinear Science, 2004,14(4):381~404
8 Hinrich N,Oestreich M,POPP K.Dynamics of oscillators with impact and friction.Chaos, Solitons& Fractals, 1997,8(4):535~558
9 Todd M D,Virgin L N.An experimental impact oscillator.Chaos, Solitons & Fractals, 1997,8(4):699~714
10 Blazejczyk-Okolewska B, Czolczynski K, Kapitaniak T,et al.Chaotic mechanics in systems with impacts and friction.World scientific series in nonlinear science series A:World Scientific Publishing Co.1999:184.
11 Peterka F,Vacik J.Transition to chaotic motion in mechanical systems with impacts.Journal of Sound and Vibration, 1992,154(1):95~115.
12 Chin W,Ott E,Helena E N,et al.Grazing bifurcations in impact oscillators.Physical Review E Statistcal, 1994,50(6):4427~4441.
13 Nordmark A B.Non-periodic motion caused by grazing incidence in an impact oscillator.Journal of Sound and Vibration, 1991,145(2):279~297
14 Bernardo M D ,Budd C J,Champneys A R,et al.Bifurcations in nonsmooth dynamical systems.SIAM Review,2008,50(4):629~701
15 金栋平,胡海岩.两柔性梁碰撞振动类型的实验研究,实验力学, 1999,14(2):129~136 (Jin D P, Hu H Y.Experimental study of the type of collision type of two flexible beams.Experimental Mechanics, 1999,14(2):129~136(in Chinese))
16 曹妍妍,赵登峰.间隙约束悬臂梁系统的动力学行为实验研究.振动与冲击, 2007,26(4):154~159(Cao Y Y,Zhao D F.Experimental study of the dynamics behavior of the clamped cantilever beam system with clearance.Journal of Vibration and Shock, 2007,26(4):154~ 159(in Chinese))
17 张磊,宋汉文.单边碰撞悬臂梁系统的实验研究和数值模拟.噪声与振动控制, 2015,35(4):25~31(Zhang L,Song H W.Experimental study and simulation of the unilateral impact cantilever beam system.Noise and Vibration Control, 2015,35(4):25~31(in Chinese))
18 边菁,徐鉴.悬臂梁限位器非线性动力学效应实验分析.动力学与控制学报, 2015,13(2):144~153 (Bian J,Xu J.Experimental study of non-linear dynamics behavior of cantilever beam system with limiting stop.Journal of Dynamics and Control, 2015,13(2):144~153(in Chinese))
19 Yingwei L,Sundararajan N,Saratchandran P.Identifica-tion of time-varying nonlinear systems using minimal radial basis function neural networks.IEE Proceedings of Control Theory Applications, 1997,144(2):202~208.
20 罗利军,李银山,李彤等.李雅普诺夫指数谱的研究与仿真.计算机仿真,2005,22(12):285~289 (Luo L J,Li Y S, Li T,et al.Study and simulation of Lyapunov exponents.Computer Simulation, 2005,22(12):285~ 289(in Chinese))
DYNAMIC EXPERIMENTAL INVESTIGATION OF AN UNILATERAL IMPACTING CANTILEVER BEAM∗
Zhu Yuan Zhang Lei Song Hanwen†
(School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China)
Based on a simple model of a cantilever beam with unilateral collision,the nonlinear dynamics of the beam under different frequencies of sinusoidal excitation is studied.The acceleration response of the free end of the cantilever beam and the impact force are measured by accelerometers and forcing transducer,respectively.Periodic,chaotic motions are also observed through the analysis of experimental results in time and frequency domain by Matlab software.It is also found of the mutation between different kinds of motions under different frequencies excitation.The largest Lyapunov exponent is also calculated by the time data of chaotic motions response.Furthermore,the transfer function between the the acceleration of the end of the cantilever beam and the impact force in the chaotic responses are found to be similar with the frequency response function in the modal test.The observation and results of this paper demonstrate the nonlinear dynamics motions,and provide a new horizon for the understanding of chaotic experimental results.
nonlinear vibration, cantilever beam, unilateral impact, periodic motions, chaotic motions
24 June 2016,revised 13 October 2016.
10.6052/1672-6553-2017-061
2016-06-24收到第1稿,2016-10-13收到修改稿.
∗国家自然科学基金资助项目(11272235)
†通讯作者 E-mail:hwsong@tongji.edu.cn
∗The project supported by the National Natural Science Foundation of China(11272235)
† Corresponding author E-mail:hwsong@tongji.edu.cn
