BP神经网络在一维降雨入渗深度的仿真应用

2017-08-28覃茂森程圣国

水力发电 2017年6期

关键词：传递函数降雨含水量

覃茂森,程圣国,刘朝,赖坡

(三峡库区地质灾害教育部重点实验室,湖北宜昌443002)

BP神经网络在一维降雨入渗深度的仿真应用

覃茂森,程圣国,刘朝,赖坡

(三峡库区地质灾害教育部重点实验室,湖北宜昌443002)

降雨引起的土体滑坡中,绝大多数滑动面都在边坡土体的最大入渗深度范围之内,快速识别降雨入渗深度对滑坡前期的预测预报具有重要的意义。以室内一维降雨入渗试验为基础,抽取表征降雨入渗深度的关键特征值,采用主成分分析法,将影响降雨入渗深度的5个特征值综合成2个主成分,基于主成分分析建立BP神经网络仿真预测模型。预测结果与实际入渗深度最大误差值仅为4.69%,说明网络性能良好。

BP神经网络；降雨；入渗深度；主成分分析

0 引言

降雨是诱发滑坡并导致人员伤亡和经济损失的一个重要外在因素[1]。降雨入渗会引起滑坡地下水位线变化和滑坡中含水率升高,造成孔隙水压力增大,基质吸力减小,导致滑坡滑动面抗剪强度不断减小,不能满足抗剪强度要求而发生失稳[2-3]。降雨引起的土体滑坡中,绝大多数滑动面都在边坡土体的最大入渗深度范围之内[4]。对最大入渗深度和滑动面的关系进行研究,可以对边坡的安全性做出初步评价,估算出滑坡规模；还有助于确定滑动面,制定合理的治理方案[4]。

众多学者提出了半理论、半经验、或者纯经验性的降雨入渗深度计算公式。张士宇等[5]分别运用李焯芬等和Pradel&Raad(1993)提出的经验法,对比计算了某非饱和高填土路堤的暴雨入渗深度发现,国外经验法更为合理；陈伟等[4]率先从能量角度推导得出最大入渗深度的计算公式；冶林茂等[6]通过对降雨量与渗透深度的数据挖掘,拟合出了适用于壤土、砂壤土和粘土的3个深度方程式,但考虑的因素稍显简单。

影响降雨入渗深度的因素众多,且各个因素与入渗深度并非呈现出简单的线性关系,难以建立一个准确的函数关系式。神经网络良好的非线性映射能力能够为这一问题提供解决思路。BP神经网络由众多神经元经由权值相互连接组成,具有大规模并行处理、分布式信息存储、良好的自组织自学习能力[9],在信息处理、模式识别、仿真预测等领域得到越来越广泛的应用。考虑到主成分分析能够把多个变量综合成少数几个主成分以反映原来众多变量包含的信息量,起到数据降维的目的[12],基于主成分分析得出的综合指标之间相互独立,互不影响,具有较好的客观性,减少了信息的交叉,经主成分分析得到的变量更适合作为神经网络输入层的输入因子。本文基于主成分分析,利用BP神经网络高度的非线性拟合能力,进行室内一维降雨入渗试验,建立了降雨入渗深度仿真预测模型,并采用神经网络BP算法，对降雨入渗深度进行仿真预测,取得了较好的效果。

1 试验设计

土样取自三峡库区,土质为粉质粘土,经风干磨碎后过2 mm筛,基本物理参数已通过试验测得。采用外径22 cm、内径20 cm、高100 cm的有机玻璃管,侧面设有5个孔,第1个圆孔中心距离玻璃管顶部15 cm,每个孔间隔15 cm。试验装置见图1。

图1 试验装置

试验开始前需要调土,将土样含水率调到初始含水率8.75%附近。填土前,在装置内部均匀涂抹凡士林,待凡士林均匀分布后装土。土样每5 cm为1层,分层装填,然后击实,土样表面打毛后开始下1层装填。待土样装填完毕后,安装传感器,静置2 h,土体水分分布稳定后,标定传感器,进行人工模拟降雨。通过侧壁变色试纸及刻度尺记录高程数据,同时采集TDR探头数据,分析土壤含水率变化情况。

2 模型建立

2.1 影响因子选取

挖掘降雨入渗时的相关数据,整理出了影响降雨入渗深度的主要因素,包括降雨总量Q、降雨历时h、降雨强度q、体积含水量m、传导率f、入渗率v、土壤、空气、人类活动等,输入因子的选取与降雨及土体含水量有关。考虑到人工神经网络要求输入特征值相互独立,故舍去降雨历时,拟采用降雨总量Q、降雨强度q、体积含水量m、传导率f、入渗率v等5个变量作为主成分分析因子。

2.2 主成分分析

整理人工模拟降雨部分试验数据,结果见表1。

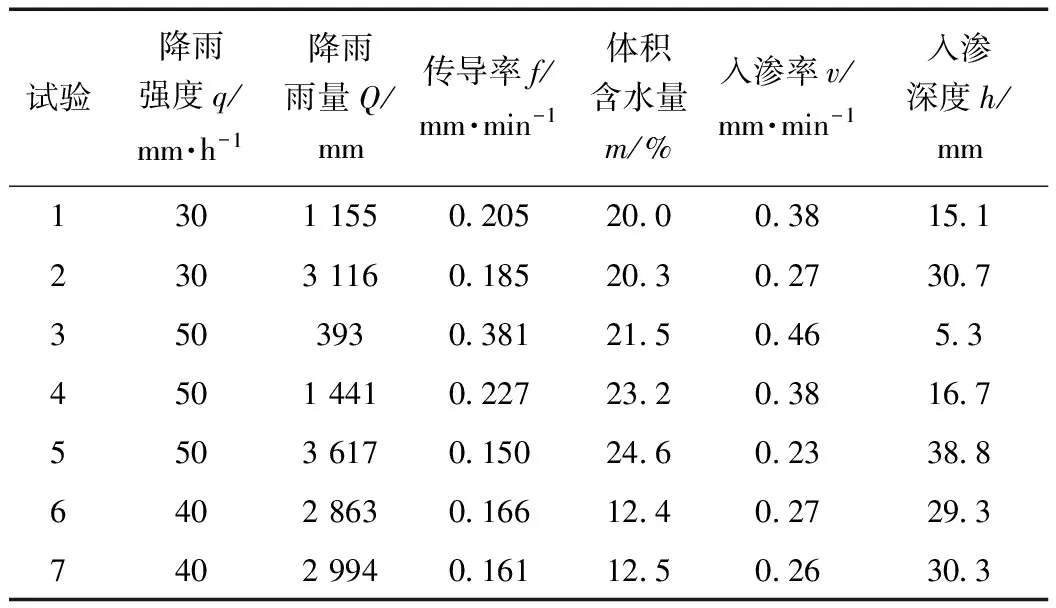
表1 试验数据

采用SPSS软件,对上述5个因子进行主成分分析。各个自变量的相关系数矩阵见表2。从表2可以知,5个因子彼此间具有不同的相关性。其中,降雨总量Q与入渗率v的相关系数为-0.987,入渗率v与体积含水量m的相关系数为-0.966,故可初步判定这些变量在反映入渗深度上的信息有一定重叠,进行主成分分析是必要的。

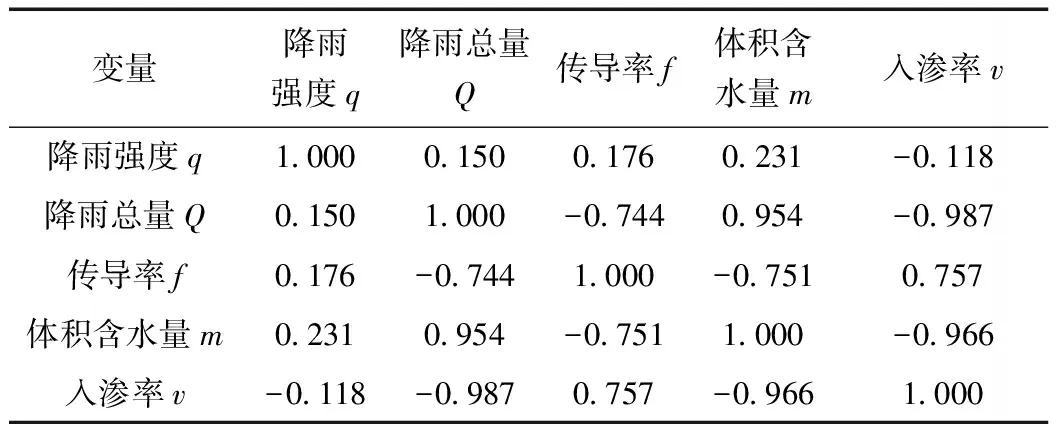
表2 自变量相关系数矩阵

主成分特征值及贡献率见表3。从表3可知,前2个因子的累计贡献率已经达到94.105%,能够代表原变量的大部分信息。通常而言,累计贡献率达到90%就能够反应其他因子的影响。由此将原变量确定为2个主成分。

表3 主成分特征值及贡献率

前2个因子的荷载矩阵见表4。从表4可知,第一主成分中降雨总量Q、体积含水量m、入渗率v的载荷系数都超过了0.97,对第一主成分贡献最大；而在第二主成分中,降雨强度q的载荷系数达到了0.977,降雨总量Q、传导率f、体积含水量m、入渗率v对因子2的贡献率均不足0.4。

表4 主要因子的载荷矩阵

由主要因子载荷矩阵求得主成分特征向量F1=[0.07 0.52 -0.44 0.52 -0.52]、F2=[0.93 0.04 0.35 0.11 -0.11]，由此得到主成分函数表达式，即

Z1=0.07X1+0.52X2-0.44X3+0.52X4-0.52X5

Z2=0.93X1+0.04X2+0.35X3+0.11X4-0.01X5式中，Z1、Z2分别表示第一、二主成分；X1、X2、X3、X4、X5分别表示数据标准化之后的降雨强度q、降雨总量Q、传导率f、体积含水量m和入渗率v。

基于以上信息，将降雨强度q、降雨总量Q、传导率f、体积含水量m和入渗率v这5个参数用2个主成分表示出来，作为BP神经网络的输入特征值。本文所建立的神经网络模型的目的是对入渗深度进行预测，故输出因子确定为降雨入渗深度值。

2.3 预测模型结构

通过上述分析,本文采用的是3层BP神经网络结构,分别是网络输入层、隐含层、输出层。网络输入变量n=2,输出变量m=1,隐含层节点数l根据经验公式进行设计,即

(1)

式中,n为输入节点数；m为输出节点数；a为1～10之间的调节常数。通过试验,本文中的隐含层节点数取值为11较为合适。

BP神经网络中常用的传递函数见图2。Log-sigmoid型函数的输入值可以是任意值,输出值在0～1之间；tan-sigmod型传递函数的输入值同样可取任意值,输出值在-1～+1之间；线性传递函数purelin的输入与输出值均可取任意值。本文中的传递函数经过学习对比确定为tan-sigmod型传递函数,训练函数取作trainlm函数。

图2 BP神经网络常用的传递函数

BP算法对误差EP和训练样本集误差E的要求是均达到最小。为了使实际输出值更接近期望输出值,可以调节BP神经网络中的阀值和各节点中的连接权值来达到预期目标。神经网路学习过程中采用大量的数据样本进行学习,本文采用了人工模拟降雨入渗试验所得的100组数据作为训练样本,12组数据作为预测样本。

3 结果分析

3.1 数据预处理

为避免网络学习时发散,在MATLAB中对数据进行归一化处理,将有量纲的数据变换为无量纲的纯量,加快训练网络的收敛速度。采用处理后的样本数据对BP神经网络进行训练,待误差低于预设值,神经网络学习过程结束。用12组主成分表示的待预测数据进行测试,结果见表5。从表5可知,在不同的网络输入值条件下,神经网络模型的预测值与实测值非常接近,误差值较小且在允许的范围内,说明神经网络学习过程是成功的,预测模型结果可靠。

3.2 数据分析

BP神经网络训练学习性能曲线见图3。从图3可知,网络收敛速度快,也没有出现震荡现象,网络性能良好,可见整个学习过程是成功的。将12组待测试数据导入网络中进行测试,将预测结果与实际入渗深度值进行对比分析发现,最大误差值为4.69%。预测误差见图4。说明在模型建立时,影响因子的选取是恰当合理的,入渗深度仿真预测模型切实可行。

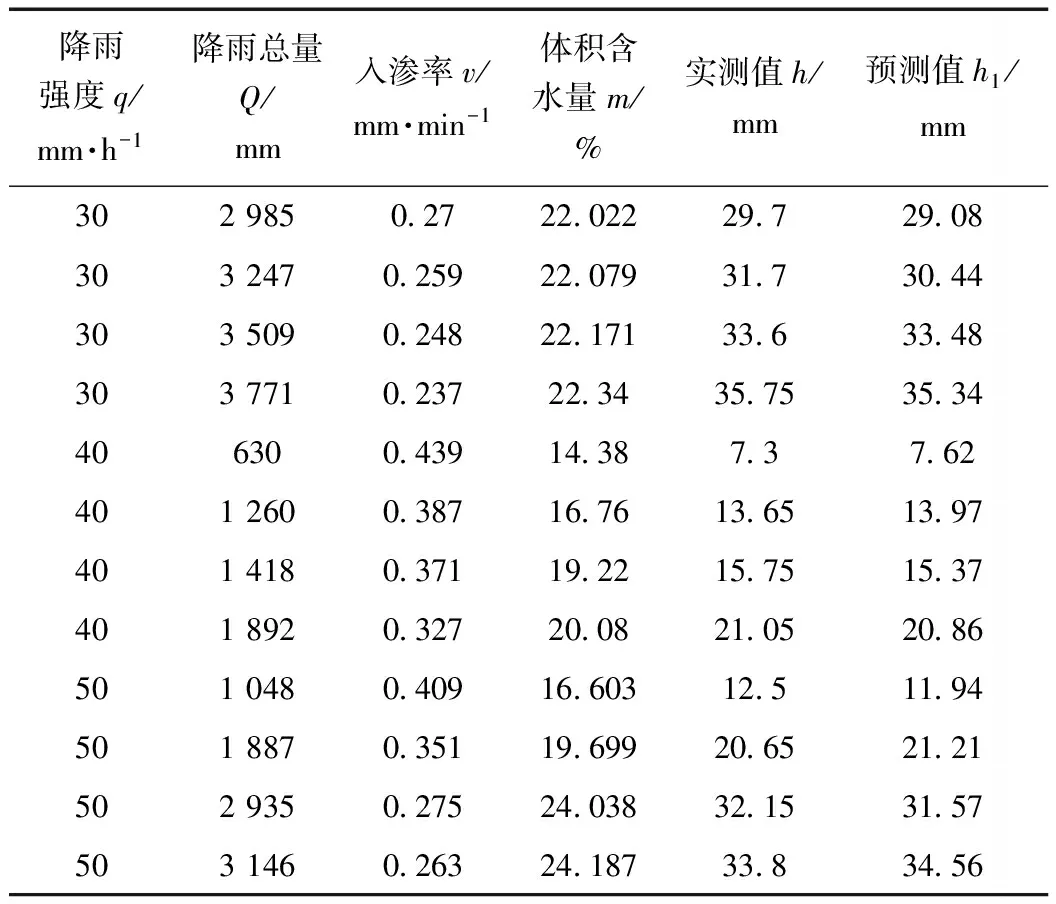
表5 深度预测

图3 网路性能

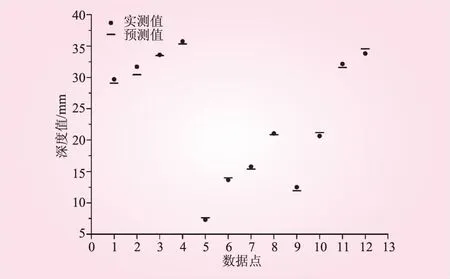
图4 预测误差

4 结语

基于主成分分析,对影响降雨入渗深度的多个变量用2个主成分表示出来,作为BP神经网络的特征输入值。利用神经网络高度的非线性拟合能力,将BP神经网络应用于降雨入渗深度仿真预测,预测模型鲁棒性强,稳定性好,结果可靠,验证了BP神经网络在降雨入渗深度的仿真应用的可行性。

神经网络能够学习和存储大量的输入、输出模式映射关系,并不需要事先揭示描述这种映射关系的数学方程,将BP神经网络应用于一些关系尚不明确、内在联系复杂的岩土工程问题是一种新的尝试。

[1]常晓军, 王德伟, 唐业旗. 中国滑坡降雨试验的研究现状与发展趋势[J]. 沉积与特提斯地质, 2010, 30(1)： 98- 102．

[2]Lam L, Fredlund D G, Barbour S L. Transient seepage model for satu-rated-unsaturated soil systems: a geotechnical engineering approach[J]. Canadian Geotehnical Journal, 1987, 24(24)： 565- 580．

[3]周家文, 徐卫亚, 邓俊晔, 等. 降雨入渗条件下边坡的稳定性分析[J]. 水利学报, 2008, 39(9)： 1066- 107．

[4]佘重九. 降雨入渗对非饱和土边坡稳定性影响研究[D]. 长沙：中南大学, 2006．

[5]张士宇, 王瑞钢. 降雨对高填土路堤的入渗深度的确定及有限元稳定分析[J]. 路基工程, 2004(5)： 17- 21．

[6]冶林茂, 薛昌颖, 杨海鹰, 等. 过程降雨入渗土壤深度的推算方法[J]. 中国农业气象, 2010, 31(Z1)： 66- 69．

[7]王磊. 人工神经网络原理、分类及应用[J]. 科技资讯, 2014(3)： 240- 241．

[8]闻新. MATLAB神经网络仿真与应用[M]. 北京：科学出版社, 2003．

[9]罗胜琪, 付金勇. 对BP神经网络算法传递函数的改进[J]. 中国科技博览, 2011(28)： 418- 418．

[10]何同弟. 高光谱图像的分类技术研究[D]. 重庆：重庆大学, 2014．

[11]贾丽会, 张修如. BP算法分析与改进[J]. 计算机技术与发展, 2006, 16(10)： 101- 103, 107．

[12]唐启义, 冯明光. DPS数据处理系统——实验设计、统计分析及模型优化[M]. 北京：科学出版社, 2006．

(责任编辑杨健)

ApplicationofBPNeuralNetworkinthePredictionofOne-dimensionalRainfallInfiltration

QIN Maosen, CHENG Shengguo, LIU Zhao, LAI Po
(Key Laboratory of Geological Hazards in Three Gorges Reservoir Area of Ministry of Education, Yichang 443002, Hubei, China)

In the landslides caused by rainfall, most of the sliding surfaces are within the maximum infiltration depth of slope soil. The rapid identification of rainfall infiltration depth has great significance to the early prediction and warning of landslide. Based on one-dimensional rainfall infiltration experiment, the key characteristic values of rainfall infiltration depth are extracted, and the principal component analysis method is used to analyze the influential factors of rainfall infiltration depth. The five eigenvalues are integrated into two principal components, and the BP neural network prediction model is established based on principal component analysis. The results show that the maximum error of prediction is 4.69%. That means the network performance is good．

BP neural network; rainfall; infiltration depth; principal component analysis