三体船与刚性体碰撞性能及结构优化研究
2017-08-28朱浩亮
朱浩亮
(常州市地方海事局,江苏 常州 213004)
三体船与刚性体碰撞性能及结构优化研究
朱浩亮
(常州市地方海事局,江苏 常州 213004)
以经典小型高速三体船为研究对象,对碰撞非线性有限元分析方法及理论进行研究。借助动态非线性有限元软件MSC.Dytran,模拟三体船整船结构模型,通过三体船主体与刚性墙之间正面碰撞,研究其在结构损伤变形、位移、速度、碰撞力和船体结构能量吸收等方面上的性能,并对三体船结构提出优化方案。通过仿真计算和比较,得出在碰撞过程中的碰撞力、速度、撞深以及能量吸收等耐撞性指标,为三体船结构优化和船舶正常航行提供参考依据。
三体船;碰撞;有限元分析;结构优化
0 引言
三体船是由主船体和2个侧体组成的多体船。与单体船相比,三体船具有航速高、操纵性好等优点,但其结构复杂,甲板宽度大。因此,三体船与刚形体碰撞产生的撞击力和单体船不同,主要和碰撞位置、船舶吨位、碰撞方向、运行速度、水的作用、刚体截面形状和尺寸等有关。即使与相同的刚体发生碰撞,如果撞击条件不同所得到的船撞力大小也各有不同[1]。此外,三体船的结构形式也将会影响撞击作用时接触面的大小和形状。本文主要研究以一定速度的三体船的主体部分与刚性体平台发生90°正面碰撞后三体船在结构损伤变形、位移、速度、碰撞力和船体结构能量吸收等方面上的性能[2],然后对比研究对三体船艏柱加强和主体内部填充泡沫后三体船在碰撞性能上的变化,进而提出三体船结构优化方案[3]。
1 碰撞非线性有限元方法及理论
1.1 隐式积分法
在20世纪80年代中期以前,对于时间域上的积分多使用纽曼(Newmark)算法,其位移、速度和加速度可以利用如下公式表达:
u(i+1)=u(i)+Δt·v(i)((1-2p)a(i)+2p·a(i+1))
(1)
v(i+1)=v(i)+Δt((1-2q)a(i)+2qa(i+1))
(2)
式(1)、式(2)中:u(i+1)、u(i)分别为当前时刻和前一时刻的位移;v(i+1)和v(i)分别为当前时刻和前一时刻的速度;a(i+1)和a(i)分别为当前时刻和前一时刻的加速度;p和q为2个待定参数;△t为当前时刻与前一时刻的时差。
1.2 显式时间积分法
时间步长的选取是显示积分算法的关键影响因素[4],时间步长即:
Δt≤Δtcr=min(Le/c)
(3)
式中:Δtcr为临界时间步长;Le为单元特征长度;c为应力波速。
采用中心差分时间积分的显式方法,计算结构系统各节点在第n个时间步结束时刻tn的加速度为:
a(tn)=M-1(P(tn)-Fint(tn))
(4)
式中:P为施加的外力(包括转化体力后的等效节点力);Fint为内力矢量,它由下面几项构成:
(5)
式中:BT为单元刚度矩阵;δ为单元节点位移;Fhg为沙漏阻力;Fcontact为接触力。
式(5)中3项依次为在当前时刻单元应力场等效节点(相当于动力平衡方程的刚度,即单元刚度矩阵与单元节点位移的乘积)、沙漏粘性阻力(为克服单点高斯积分引起的沙漏问题而引入的粘性阻力)以及接触力矢量。
节点的速度和位移矢量通过下面两式计算:
v(tn+1/2)=v(tn-1/2)+0.5a(tn)(Δtn-1+Δtn)
(6)
u(tn+1)=u(tn)+v(tn+1/2)Δt
(7)
式中:v(tn+1/2)为tn+1/2时刻节点的速度;v(tn-1/2)为tn-1/2时刻节点的速度;a(tn)为tn时刻节点的加速度;Δtn-1和Δtn为时间步,其计算公式见式(8)、式(9);u(tn+1)和u(tn)分别为tn+1和tn时刻的位移。
时间步和时间点的定义为:
Δtn-1=(tn-tn-1),Δtn=(tn+1-tn)
(8)
Δtn-1/2=0.5(tn+tn-1),Δtn+1/2=0.5(tn+1+tn)
(9)
式中:tn+1、tn和tn-1分别为(n+1)时刻、n时刻和(n-1)时刻的时间点。
下一时间点上的模型几何形状由前一时间点位置决定,即:
Xt+Δt=X0+ut+Δt
(10)
式中:X0为初始时刻模型的集合形状;Xt+Δt为t+Δt时刻模型的集合形状;ut+Δt为t+Δt时刻内模型移动的位移。
2 三体船碰撞方案
由于高速三体船由主体、附体以及连接桥组成,在建模过程应考虑整船建模。本节进行全船碰撞有限元数值仿真的船舶为7 m高速三体船,艏柱板厚为6 mm。船体的有限元模型的单元数为3 652个,节点数为2 698个。利用MSC.Dytran软件对7 m高速三体船整船碰撞模型进行数值仿真分析,研究其耐撞性能。假设船舶之间有10 mm的初始距离,船舶以12.86 m/s的初速度正向撞击刚性体,其碰撞方案如图1所示。三体船采用玻璃钢材料加工,在MSC软件中可以直接从材料数据库中获得材料数据[5]。本文利用MSC.Dytran软件的数值仿真分析对7 m高速三体船整船进行模拟碰撞,研究其耐撞性能。
3 碰撞性能分析
3.1 三体船碰撞性能
本节三体船以12.86 m/s速度,主体部分与相距10 mm的刚性体平台发生90°正面碰撞。三体船在结构损伤变形、位移、速度、碰撞力和船体结构能量吸收等方面上的性能如图2所示。
从图2可看出:
(1)撞击船艏部碰撞损伤区域主要集中在船艏部。撞击船的外板、甲板和艏柱与刚形体均发生了直接碰撞。因此,要提高船舶的耐撞性能,除对甲板结构进行加强外,还需要考虑对艏柱结构的加强,进而提高整个艏部结构整体的耐撞性能[6]。
(2)随着碰撞进行,甲板、船底板以及内部结构都参与碰撞,对船舶速度的阻碍作用越来越大,速度呈现明显下降趋势。
(3)撞击船的位移曲线呈上升趋势。随着碰撞的进行,曲线变化斜率越低,说明碰撞受到的阻碍也越大。
(4)碰撞力曲线总体上具有明显的非线性,呈多峰状态,且峰值处为船体接触区域的主要构件失效时刻。在t=0.1 s时,碰撞力达到极值7.2×105N。随着往后时间的推移,碰撞力呈现下降趋势。
(5)在相同的碰撞时间内,不同构件的能量吸收曲线呈现上升趋势。随着碰撞的进行,同一构件抵御碰撞的能力逐渐增加,总的变形能也随之增大。碰撞结束后各构件总吸能为140.5 kJ,其中舷侧外板是主要吸能构件,吸能量约占总吸能量的35%,而船底、甲板和其余构件的能量吸收分别占总能量的23%、20%和22%。可见要想提高耐撞性能也可以对这些构件进行加强[8]。
3.2 艏柱加强对三体船碰撞性能的影响
基于前面船舶碰撞力学机理的研究,对高速三体船进行艏柱加强,即增加艏柱板厚,由原来的6 mm增加到8 mm。通过仿真计算和比较,三体船在结构损伤变形、位移、速度、碰撞力和船体结构能量吸收等方面上的性能如图3所示。
从图3可看出:
(1)与未采取加强前船体碰撞的结构损伤变形相比,加强后的损伤变形范围减小,撞深减小,甲板破裂延迟。
(2)碰撞结束后各构件总吸能141 kJ,其中舷侧外板占总吸能的61%。与未加强的船体结构相比,舷侧外板吸能比例增加了10%。这是由于艏柱厚度增加的结构设计使结构损伤变形迅速扩大到了
一定程度,从而降低了甲板和内部其他构件的吸能情况。单从吸能角度来讲,艏柱厚度的变化改变了整船吸能情况,同时也改变了船体的损伤变形。
3.3 主体内部填充泡沫后对三体船碰撞性能的影响
基于上述船舶碰撞力学机理的研究,对高速三体船主体内部填充泡沫。泡沫材料的主要作用是在保证强度的情况下减轻重量,提高弯曲刚度[9]。Fr19~Fr23肋位之间填充泡沫材料如图4所示。通过仿真计算和比较分析三体船在结构损伤变形、位移、速度、碰撞力和船体结构能量吸收等方面上的性能如图5所示。
从图5可看出:
(1)加强后的损伤变形范围有所减小,撞击时间延迟,位移量变大。
(2)在碰撞的开始阶段,由于碰撞的位置发生在主体首部区域处,所以舷侧外板吸收了较多的能量。但随着参与变形的外板的范围不断扩大,泡沫、船底和甲板等逐渐成为主要的吸能构件,碰撞结束后各构件总吸能153 kJ,其中泡沫占总吸能的11%。从图中可以看出,主体内部填充泡沫对整船的能量起到了一定的作用。
本文提出了2种新的结构加强方案。方案Ⅰ:增加艏柱板厚;方案Ⅱ:在Fr19~Fr23肋位之间填充泡沫材料。现将它们与未加强前的7 m高速三体船抗撞性能进行比较研究,碰撞结果汇总见表1。
4 结论
本文主要研究高速三体船与刚性体发生碰撞以及艏柱加强后三体船碰撞性能的研究,通过数值仿真计算的方法,结合表1整理碰撞结果可以得到以下结论:
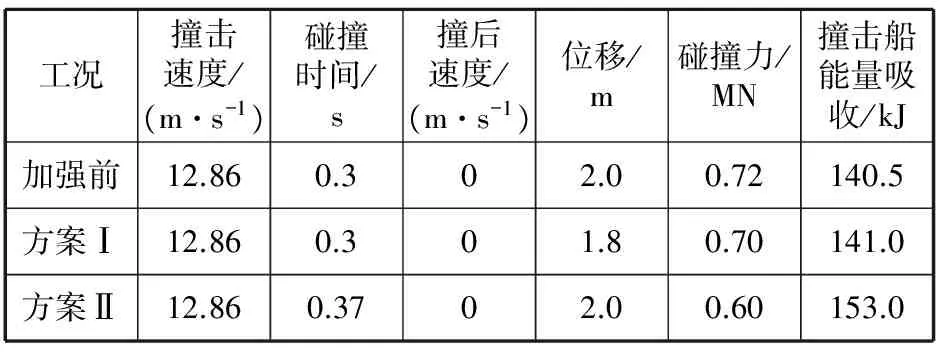
表1 碰撞结果汇总
(1)主体内部填充泡沫的三体船的能量吸收能力最高,相比加强前的船体结构吸能,增加10%。
(2)表中3种情况下的撞击时间也有明显差异。方案Ⅱ的碰撞时间最长,主要因为是泡沫材料提高板材抗局部弯曲性能,极好地吸收和传递外部冲击和破坏。泡沫同时均匀地传递剪切力到相邻的结构上,避免大量分散的结构支撑件。
(3)方案Ⅱ最大碰撞力最低。2种加强方案进行比较,发现方案Ⅱ的抗撞潜能发挥了很大作用。
[1] 黄毅铭. 船舶舷侧新型耐撞结构研究[D]. 镇江:江苏科技大学, 2014.
[2] 宗莉娜, 刘伟庆, 方海,等. 船桥碰撞中各因素对船撞力影响的研究[J]. 江苏船舶, 2016, 33(6):9-12.
[3] 高书清, 陶延武. 37 m黄河双体渡船总强度有限元分析[J]. 江苏船舶, 2014, 31(6):14-16.
[4] 尚晓江, 苏建宇, 王化锋. ANSYS/LS-DYNA动力分析方法与工程实例[M]. 北京:中国水利水电出版社, 2008.
[5] 李毅. 轻质夹层复合结构稳定性及冲击性能分析[D]. 西安:西北工业大学, 2007.
[6] Wei Q S, Jones N. Dynamic plastic response and failure of a clamped beam struck transversely by a mass[J]. International Journal of Solids & Structures, 1993, 30(12):1631-1648.
[7] 王健伟. 基于非线性有限元方法的船舶-冰层碰撞数值研究[D]. 上海:上海交通大学, 2015.
[8] Tabri K, Broekhuijsen J, Matusiak J, et al. Analytical modelling of ship collision based on full-scale experiments[J]. Marine Structures, 2009, 22(1):42-61.
[9] 江华涛. 船舶碰撞与缓冲船首结构研究[D]. 上海:上海交通大学, 2002.
2017-01-25
朱浩亮(1980—),男,工程硕士,注册验船师,从事船舶碰撞研究。
U661.4
A
