通过合理引导打败物理学习中的纸老虎

李转　刘春梅

【摘 要】大學物理被学生认为是最难最头疼的一门基础课。本文建议在大学物理教学中，针对学生认为的难点，通过选择合适的方法与例题，抽茧剥丝，解开这些难点纸老虎的神秘面纱，教会学生打败纸老虎，克服物理学习中的畏难情绪。并进行举例。

【关键词】毕奥萨伐尔定律；大学物理；课堂教学；矢量叉积

大学物理是一门非常重要的基础理论课，它既要传授学生物理学基本知识，又能培养他们良好的思维习惯以及敢于突破传统的创新精神和解决问题的能力。然而在十多年的教学中，听到学生说的最多的就是大学物理难学。笔者曾经做过问卷调查，51%的学员认为大学物理是让他们最头疼的基础课程，他们甚至给出了千古绝对：提锡壶游西湖，锡壶掉西湖，惜乎锡壶；学物理如雾里，雾里看物理，勿理物理。

其实物理学中的很多问题、很多难点都不过是纸老虎，都是以最基本、最简单的原理为基础的，有一定的方法和规律可循的。但是如何让学生认识到这一点，克服畏难情绪，打败这些纸老虎，掌握方法树立学习的信心呢？笔者希望通过本文的探讨与举例，结合课上课下帮助学员正确的看待物理学中的难点，解开纸老虎的神秘面纱，养成良好的学习习惯，尽快掌握大学学习方法，提高自主学习的能力。

1 原因分析

学生觉得大学物理难学，主要是因为以下三个原因：1）大学物理中要解决更复杂更实际的问题，引入新方法，增加新的定理公式，这让学生用起来有些茫然。2）大学物理中大量用到微积分，尤其是多个变量情况下的积分是学生的一个难点。3）矢量的大量使用。

经过一段时间的学习，他们基本能够接受使用矢量描述，两个矢量点积是标量，只有大小没有方向，学生也还乐意接受，但是内心很排斥矢量的叉积。如果叉积后还要积分且是多个变量的积分问题基本上被他们认为是最难的问题。但是引入微积分和矢量解决实际问题是大学物理与中学物理的最大区别，是大学物理学习中不可能避免和逃避的。那么叉积真的总是添乱的吗？未必，实际上如果认真分析你会发现，叉积在一些特殊情况下也会带给大家一些方便，体现出它的优势来的。

2 寻找方法

教学方法是影响老师执教能力的关键，老师有义务综合运用各种教学方法，有效地服务于课堂教学，充分调动课堂上老师和学生的情绪，并使教学内容和形式上更具趣味性和针对性。目前流行的翻转课堂、导学式教学等在军校里都很难实施，因为这些方式都需要较多课外时间，而由于军校管理的特殊性，学员可自主支配的时间很少，能很好地完成课前探索研究学习的学员并不是很多，实施起来还存在很大的困难。所以充分发挥好传统教学的优势，适时、适度地补充现代化的、信息化的教学手段则才是比较符合实际的选择。

如果学生在课前预习的过程中能够及时反馈他们遇到的难点，比如可以建立微信群，学员可以对预习情况进行及时反馈，老师对反馈的信息进行梳理，找准学生的困难点，在课堂教学中就可以抽茧剥丝，教会学生打败这些纸老虎，让学生能够不怕物理，好学物理，学好物理，爱上物理。

3 典型案例

电学和磁学是大学物理非常重要的两个模块，但是学生普遍觉得磁学比电学要难得多。学生说他们是被比奥萨法尔定律吓倒了。比奥萨法尔定律简称比萨定律，是磁学部分的第一讲，用它可以求载流导线周围的磁感强度，地位等同于电学中的库仑定律，是磁学中非常重要的基本定律，但在它的身上非常完美的聚结了以上的三个困难。通过学生的预习反馈可以看到学生的问题主要集中在：电流元的磁感应强度d■为什么是一个叉积的结果？叉积后的方向积分时如何处理？多变量积分时，要把多个变量换成同一个变量，换成哪个好呢？根据学生的反馈信息，老师课前要进行梳理，找出老虎。针对不同的问题，分别用不同的工具和方法，在授课过程中引导学生逐步解决这些困难，揭开老虎的面纱。

对于d■的方向是一个叉积的结果，可以采用模拟展示的方法，形象直观的给出这一方向。比萨定律里的叉积和叉积后积分是最让学生头疼的，要选好例题，抽丝剥茧，对学生进行引导。通过合理的选择例题可以看出在某些情况下，叉积反而使问题简单化，体现叉积优势，并在计算过程中引导学生学会统一变量。由浅到深的学，树立解决此类问题的信心。

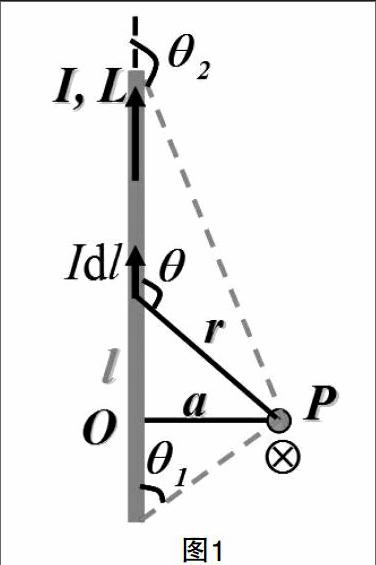
在授课中，以直线电流的磁场为例。类比电场，先求电流元的磁场，由毕奥萨伐尔定律，电流元Id■在空间一点产生的磁感应强度为d■=■，然后根据场的叠加原理对d■进行矢量积分。这里有一个矢量的叉乘，该怎么积分呢？

图1

先来看一下d■的方向，是d■×■的方向，根据右手螺旋法则，电流元Id■在p点的磁场方向是垂直于纸面向里的。改变电流元Id■的位置，你就发现，导线上任意一电流元在P点产生的磁场具有相同的方向，因此所有电流元在该点产生的磁感应强度的方向就是垂直于纸面向里的，对矢量d■积分时，只需要对d■的大小直接积分就好了。那么到这里你是不是有突然爱上叉乘的感觉呢？

这样问题就变得简单了。如果夹角用？兹表示，电流元Idl在p点产生的磁场大小为：

dB=■

然后对dB进行积分。该如何积分呢？这里是对dl积分，但是不同位置处的电流元对应不同的？兹角和不同的r，也就是说这一积分中l、？兹、r都是变量，要积分首先就要利用几何关系统一积分变量， l、？兹、r集中在一个直角三角形中，其中a是已知的，而l和r都很容易用a和？兹表示出来， 所以最后可以统一变量至？兹：

dB=■sin？兹d？兹

再往下的积分计算就很简单了。至此，困扰学生的问题和困难就一一解决了。讲课过程中要善于比较带电导线的电场的求解，通过对比体现叉积计算的优势。

4 小结

再回头看看我们都是怎样克服这些困难的：第一、新概念老方法，类比电场先找电流元的磁场，再用场的叠加原理求磁场；第二、矢量叉乘并不可怕，在某些情况下反而可以利用叉乘优势使问题简化，比如这里所有电流元在p点产生的磁场方向都相同；第三、当有多个积分变量时，寻找变量间的几何关系，统一积分变量。可见只要用对了方法，这些所谓的难点都不过是些纸老虎而已。这种打败纸老虎的方法可以有效地消除学生学习物理的为难情绪，使他们逐渐学会处理疑难问题的方法，还可以使学习者更快的适应新的挑战。

【参考文献】

[1]张三慧，编著.大学物理学（第三版）B版[M].北京：清华大学出版社，2009.

[2]张爱清，叶新荣，丁绪星.实例教学法在“电磁场与电磁波”教学中的应用[J].中国电力教育，2010，34.

[责任编辑：田吉捷]