计及风速与风机故障相关性的概率潮流计算

叶嘉俊，魏焕政，李牧星

（广东工业大学自动化学院，广东 广州 510006）

计及风速与风机故障相关性的概率潮流计算

叶嘉俊，魏焕政，李牧星

（广东工业大学自动化学院，广东 广州 510006）

针对计及风速与风机故障不确定性及相关性的风电并网电力系统概率潮流计算问题，基于Nataf变换建立了能够同时考虑风速、风机故障不确定性和相关性的风电场出力模型，提出一种可灵活处理风速与风机故障相关性的Monte Carlo概率潮流计算方法，并引入“拉丁超立方抽样”技术提高抽样效率，降低计算复杂度。仿真结果表明：该方法能反映风电场出力的实际情况，合理评估风电并网对电力系统概率潮流的影响，有助于风电场的选址及电网规划。

相关性；Monte Carlo法；Nataf变换；概率潮流；拉丁超立方抽样

新能源发电是解决世界能源危机和环境污染问题的有效途径。风能作为高效清洁的新能源具有取之不尽、用之不竭的特点，近年来得到了大规模应用，截至2016年上半年，仅我国风力发电装机容量就已达137.08 GW［1］。风机作为风力发电系统的核心部件之一，已被大量安装以获取更多的风能。随着新技术的发展，风机的尺寸不仅越来越大，而且结构和功能也变得越来越复杂，这给电力系统的规划和运行带来了很多不确定性因素，也对传统的电力系统分析与计算提出了挑战［2］。

由于风机大多安装在环境恶劣的偏远地区，维护不便，因而其强迫停运率远高于常规机组；且同一风电场内风机的故障与风速存在一定的正相关性［3-4］，在风电大规模并网时，这种不确定性和相关性因素会对电力系统可靠运行产生不可忽视的影响［5］。因此，对含风电并网电力系统进行概率潮流研究时，要考虑风速与风机故障的不确定性及其之间的相关性。

1 研究现状及需解决的问题

风电并网对电力系统概率潮流（Probabilistic Load Flow，PLF）的影响已有诸多研究成果：文献［6-7］在风电场建模过程中考虑了风速不确定性，并分析了风电不确定性对电力系统概率潮流的影响。文献［8］建立了同时考虑尾流效应和地形因素的风电场综合模型，分析了风电并网运行对系统概率潮流的影响。文献［9-11］分析了不同风电场间风速相关性对电力系统概率潮流的影响。文献［12］建立了多风电场的概率潮流模型，建模时同时考虑了风速相关性和负荷相关性。文献［13］研究了风电、光伏发电和电动汽车并网对电力系统概率潮流的影响。

虽然风电并网对电力系统概率潮流影响的研究已有大量成果，但还存在以下问题：

（1）在潮流计算建模时没考虑风机故障与风电场风速的不确定性及相关性。

（2）考虑相关性问题的随机抽样方法效率低下，加大了Monte Carlo概率潮流计算方法的复杂度，降低了计算效率。

（3）现有研究没有考虑风机故障与风速的不确定性和相关性对系统潮流分布的影响。

而上述问题的存在，使现有对含风电并网电力系统概率潮流的研究不够准确，不利于风电场的选址及电网规划。因此寻找一种考虑风电场风速与风机故障不确定性和相关性的PLF计算方法，研究风速与风机故障对系统PLF的影响就显得极为迫切和必要。

2 考虑风速和风机故障相关性的概率潮流计算方法

为研究风速与风机故障相关性对电力系统概率潮流的影响，本文提出一种能够同时考虑风速和风机故障不确定性及相关性的风电场建模方法。在此基础上，采用Monte Carlo模拟和中值拉丁超立方抽样技术（Latin Hypercube Sampling，LHS）［14］的概率潮流计算方法对含风电并网电力系统进行概率潮流计算，分析风速与风机故障相关性对电力系统概率潮流的影响，为风电场的规划和运行提供参考。

2.1 考虑不确定性和相关性因素的风电场出力建模

2.1.1 风电场建模中的不确定性和相关性因素

2.1.1.1 风电场风速的不确定性

国内外学者针对风速不确定性的特点其进行了大量研究［15-16］。研究表明，世界上大部分地区的风速都可采用双参数的Weibull分布函数来描述其分布规律，其概率密度函数［17］为

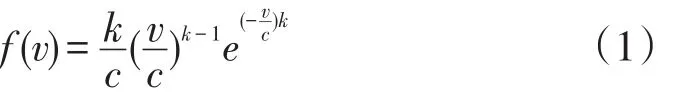
式中：v、k、c—分别代表风速、Weibull分布的形状参数和尺度参数，其中c反映了风电场平均风速的大小。

由式（1）可得风电场风速的累计概率分布函数

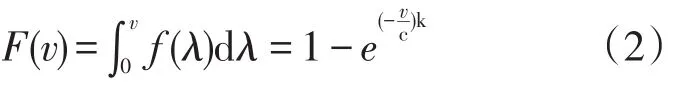
2.1.1.2 风机故障的不确定性

与常规机组相比风机结构相对简单，计划检修通常安排在低风速时期，检修时间短，因此在进行概率潮流分析时可以不考虑风机计划检修状态，通常采用两状态启停模型来描述风机的随机停运。其强迫停运率表示为

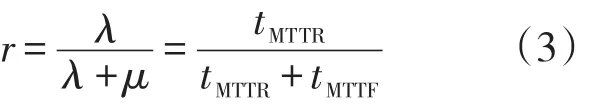
式中：λ、μ、tMTTR、tMTTF—分别代表风机的失效率、修复率、平均无故障运行时间及平均修复时间。

因此，风电场中发生故障的台数近似服从二项分布，其故障概率［18］可表示为

式中：m，n—分别表示风电场风机总数和发生故障风机台数。

2.1.1.3 风速与风电机组故障间的相关性

风电场整体出力会受到风速和风机故障相关性的影响，因此在风电场出力建模时要计入这种相关关系。本文采用风机故障数与风速的正相关性来等效处理风电场内风机故障与风速间存在的相关关系，即：风速越强，同一时刻停运的风机数目越多。

2.1.2 考虑风速与风机故障的风电场出力模型

风机输出功率Pv（t）是风力发电机组的重要性能指标，与风速（v）和风机自身的功率特性密切相关［19］。一般来说，Pv（t）和v之间的关系可表述为

式中：pr—表示风机的额定输出功率；

vci、vr、vco—分别表示风机的切入风速、额定风速和切出风速；

A、B、C—vci、vr和vco的函数，可由式（6）求得。

假设风电场采用恒功率因数控制方式，则风力发电机从电网吸收的无功功率Qv可表示为

式中：φ—功率因数角。

由此，可得t时刻考虑风机故障的风电场输出功率Pw（t）和吸收的无功功率Qw（t）为

式中：m、n(t)—分别表示风电场中风机的数量和风电场t时刻故障风机数目。

2.2 风速和风机故障相关性的随机抽样方法

为建立含风电并网电力系统概率潮流计算模型，需要模拟产生风电场风速及其故障风机数目样本，但对于存在相关关系的风速和风机故障数目而言，无法通过直接抽样的方法产生随机样本。为此，本文基于Nataf变换产生考虑风速与风机故障相关性的随机样本，首先产生具有独立性的标准正态随机样本；然后，基于等概率原则和Cholesky分解技术将相互独立的随机样本转换为具有相关关系的风速和风机故障的随机样本。

2.2.1 Nataf变换

假设m维输入随机变量为X=[x1,…,xi,…,xm]T，且其相关系数矩阵为：

式中：σxi、σxj—分别为随机变量xi、xj的标准差；

Cov(xi,xj)—随机变量xi和xj的协方差。

设具有相关性的标准正态随机变量向量Z=[z1,…,zi,…,zm]T的相关系数矩阵为

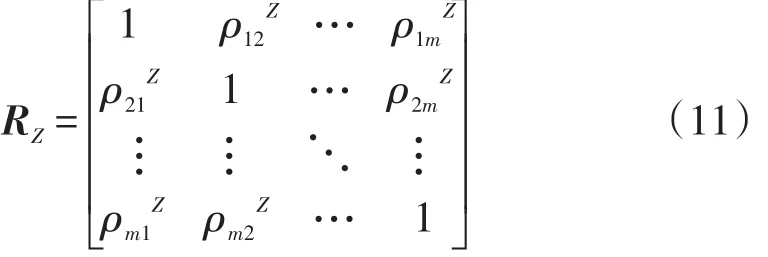
根据式（12）所示等概率原则可将X转化为具有相关性的标准正态随机变量向量Z。

式中：Φ(∙)—标准正态变量z的累积分布函数；

F-1(∙)—变量x的累积分布函数的反函数。

式中：Φ(zi,zj,ρ)—表示相关系数为的标准二元高斯分布的概率密度函数；

μi、μj、σi、σj—分别为变量xi、xj的期望和标准差。

在已知ρijx的情况下，可通过Monte Carlo模拟法求得，详细求解步骤见文献［20］。

以上步骤实现了从相关输入随机向量到具有相关性标准正态随机向量的变换。只要Z的协方差矩阵RZ已知，那么可通过式（14）将Z转换为独立的标准正态随机向量。

式中：U=[u1,…,ui,…,um]T—独立标准正态空间的随机向量；

L—是Cholesky分解（式（15））得到的下三角矩阵。

2.2.2 风速和风机故障相关随机样本的抽样步骤

2.2.1 节介绍了Nataf变换如何将相关的随机向量转换为相互独立的标准正态随机向量，那么根据其逆过程即可将相互独立的标准正态随机样本转换为具有相关关系的风速、风机故障随机样本。此外，本文引入LHS来提高随机样本的抽样效率。综上，风速、风机故障相关随机样本抽样的基本步骤如下：

（1）读入风速、风机故障的概率模型信息及相关系数，并设定采样规模m；

（2）基于LHS生成相互独立的标准正态分布随机变量向量Umx1的样本U；

（3）根据式（11）、式（13）由风速与风机故障的相关系数矩阵RX计算得到具有相关性的标准正态分布随机变量向量Z的相关系数矩阵RZ，并对其进行Cholesky分解（式（15）），得到下三角矩阵L；

（4）通过式（16）得到相关系数矩阵为RZ的标准正态分布随机变量向量Zmx1的样本Z；

（5）通过等概率转换原则（式（12））即可生成相关系数矩阵为RX的风速和风机故障随机样本。

抽样流程如图1所示。

图1 风速和风机故障相关随机样本抽样流程

2.3 基于Monte Carlo模拟的概率潮流计算方法

结合本文所提的考虑风速和风机故障相关性的随机抽样方法，采用Monte Carlo模拟法求解含风电并网电力系统概率潮流的方法步骤如下：

（1）输入配电网的结构参数、风速和风机故障的相关系数及其概率模型信息（分布类型及相关参数），并设定LHS的采样规模s；

（2）根据2.2节中的风速、风机故障相关随机样本的抽样步骤产生具有相关关系的风速、故障风机数目的随机样本；

（3）采用Newton-Raphson算法依次进行s次确定性的潮流计算，得到节点电压、支路潮流和网损等多组计算值；

（4）应用统计学的方法统计节点电压、支路潮流等输出随机变量的样本信息，并绘制各输出变量的概率分布曲线。

计算流程如图2所示。

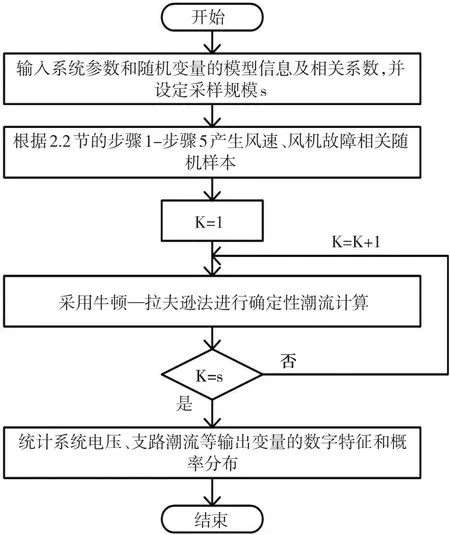
图2 基于Monte Carlo模拟的概率潮流计算流程

3 仿真结果与分析

3.1 算例系统说明

为分析风速与风机故障相关性对电力系统概率潮流的影响，本文采用改造后的IEEE-30节点标准测试系统进行仿真分析，如图3所示。假设一风电场接入到节点25，风电场风速服从的尺度参数为8，形状参数为2.2的Weibull分布，并含有20台额定功率为5 MW的风电机组，且风机的切入、额定、切出风速分别为3 m/s、10 m/s和25 m/s；结合当前风机的可靠性水平，风机强迫停运率r取5%［19］。

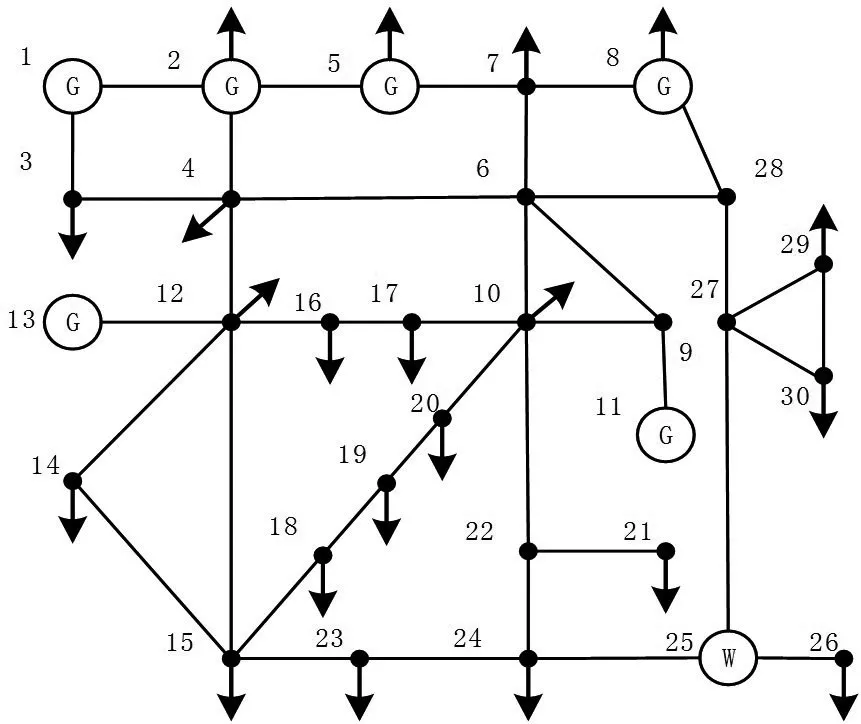
图3 IEEE-30节点算例结构

3.2 所提概率潮流计算方法的验证

采用本文概率潮流计算方法对图3所示IEEE-30节点标准测试系统进行概率潮流分析，并与随机采样的Monte Carlo模拟法（认为该方法所得结果为准确值）得到的结果进行比较（验证本文所提方法的准确性），其中LHS的采样规模为1 000次，随机采样规模为50 000次。

两种方法所得节点25的电压期望值μv、标准差σv；线路10-20有功功率的期望 μa、标准差σa；系统网损的期望 μI、标准差σI如表1所示。由表1可知，两种方法所得结果基本一致，说明本文方法是准确的；另外，采用本文方法时计算时间为19.72 s，采用随机采样的Monte Carlo模拟法时计算时间为1 367.77 s，本文方法具有较高的计算效率。

表1 IEEE-30节点系统的概率潮流计算结果

3.3 风速与风机故障相关性对系统概率潮流的影响分析

为分析风速与风机故障相关性对电力系统概率潮流的影响，本文将风速与风机故障之间的相关系数分别设为0、0.3、0.6和0.9，并采用本文所提基于LHS的Monte Carlo模拟法依次计算概率潮流。

3.3.1 对节点电压的影响

系统各节点电压的期望值、标准差在不同风速与风机故障相关系数下的变化曲线如图4所示。

图4 节点电压期望值和标准差

由图4可知，随着风速和风机故障间相关程度的变化，系统各节点电压的期望值几乎没有变化；但标准差变化明显，且标准差随着相关程度的增加而增加。这是由于风速和风机故障间相关程度的增强会使风电场功率变化的同步性增强，因此随着相关程度的增加系统各节点电压的波动性也随之增加。节点25电压的概率密度曲线和累积分布曲线如图5所示。

图5 节点25电压的概率密度曲线和累积分布曲线

由图5可知风速和风机故障相关性对节点电压的概率分布有较大影响，随着相关性的增加，节点电压的波动程度也随之增加，且对低压段影响尤为明显。

3.3.2 对线路有功功率的影响

系统各线路有功功率的期望值、标准差在不同相关系数下的变化曲线如图6所示。

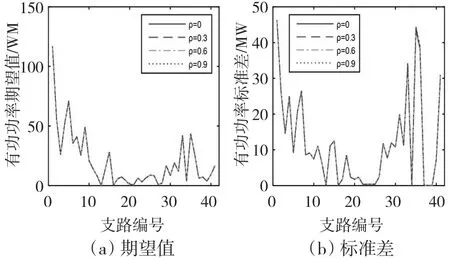
图6 线路有功功率的期望值和标准差

由图6可知，随着风速和风机故障间相关程度的变化，系统各线路有功功率的期望值和标准差几乎没有变化。

线路10-20有功功率的概率密度曲线和累积分布曲线如图7所示。

由图7可知风速和风机故障相关性对线路传输功率低压段的概率分布有一定影响，且相关程度越强影响越大。

图7 线路10-20有功功率的概率密度曲线和累积分布曲线

3.3.3 对网损率的影响

IEEE-30节点标准测试系统的网损率在不同风速、风机故障相关系数下的标准差与期望值如表2所示。由表2可知，随着风速与风机故障相关程度的加强，系统网损率期望值从8.316 5%变到了8.617 6%最大变化幅值和最大变化率分别为0.301 1和3.620 5%；标准差从4.7409%增加到了5.2155%，最大变化幅值和最大变化率分别为0.474 6和10.01%。

表2 网损率的期望值与标准差

不同相关系数下，网损率的概率密度曲线和累积分布曲线如图8所示。

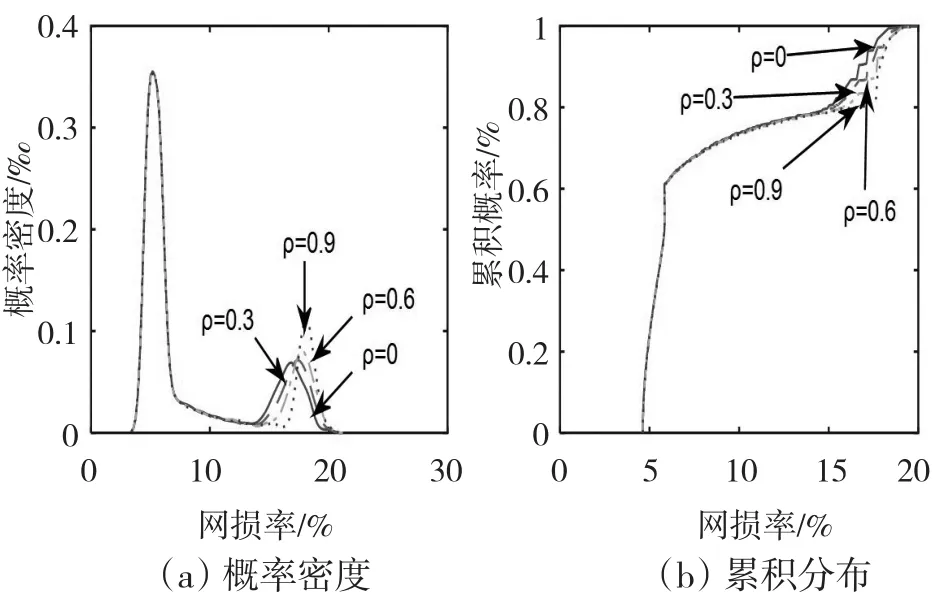
图8 系统网损的概率密度曲线和累积分布曲线

由图8不难看出，风速与风机故障间的相关关系会对系统网损率的概率分布产生影响，且相关程度越强影响越大。

4 效果评价

（1）由仿真结果与分析可知，本文提出的风电场出力建模方法可有效考虑风电场风速与风机故障的不确定性及相关关系，且基于Nataf变换的随机抽样方法能够模拟产生具有相关性及不确定性的风速和风机故障样本，具有较好的工程应用价值。

（2）由3.2节可知，本文引入LHS技术后降低了随机采样的蒙特卡罗PLF计算复杂度，提高了计算效率，且保持了PLF计算的准确度。

（3）由图4-图8及表2可知，本文所提概率潮流计算方法可准确计算出风速与风机故障不确定性及相关性对系统节点电压、支路潮流及系统网损率等输出随机变量的期望值、标准差及概率分布等指标的影响，克服了传统PLF计算方法没有考虑风速与风机故障不确定性及相关性的缺点。

5 结论

（1）本文建立的概率潮流计算模型，充分考虑了风电场运行过程中的不确定性及相关性因素，包括：风速、风机故障的不确定性及风速与风机故障间的相关性，建立的模型更能反映风电场出力的实际情况，减小了误差。

（2）引入LHS技术提高了采样效率，使Monte Carlo概率潮流计算方法在保持计算准确度的同时降低了计算复杂度，提高了计算效率。

（3）仿真结果表明：风速、风机故障间的相关性对电力系统节点电压、线路传输功率及网损率等指标的期望值影响较小，但对这些指标的标准差和概率分布有较大影响，且相关程度越强，波动性越大。对含大规模风电并网电力系统进行概率潮流分析时，考虑风速、风机故障间的相关性，可以更合理地评估风电并网对电力系统运行的影响，有助于风电场的选址及电网规划。

［1］ 国家能源局.2016年上半年风电并网运行情况[EB/ OL].(2016-07-27).http://www.nea.gov.cn/2016-07/27/ c_135544545.htm.

［2］ 薛禹胜,雷兴,薛峰,等.关于风电不确定性对电力系统影响的评述[J].中国电机工程学报,2014,34(29): 5029-5040.

［3］ Peter T,Clare E,Andy B,et al.Influence of Wind Speed on Wind Turbine Reliability[J].Wind Engineering, 2006,30(1):55-72.

［4］ Su C,Jin Q,Fu Y.Correlation analysis for wind speed and failure rate of wind turbines using time series ap⁃ proach[J].Journal of Renewable&Sustainable Energy, 2012,4(3):265-269.

［5］ 陈凡,卫志农,张小莲,等.计入风速与风电机组故障相关性的风电场可靠性建模及其应用[J].中国电机工程学报,2016,36(11):2900-2908.

［6］ 董雷,程卫东,杨以涵.含风电场的电力系统概率潮流计算[J].电网技术,2009,33(16):87-91.

［7］ Gu W D,Shi L B,Yao L Z,et al.Probabilistic load flow calculation considering wind power uncertainty[C]//In⁃ternational Conference on Power System Technology.Chengdu,Chian,2014:909-915.

［8］ 郑睿敏,李建华,李作红,等.考虑尾流效应的风电场建模以及随机潮流计算[J].西安交通大学学报, 2008,42(12):1515-1520.

［9］ Chen C,Wu W,Zhang B,et al.A new point estimate method for probabilistic load flow with correlated vari⁃ables including wind farms[C]//IEEE Power&Energy Society General Meeting.National Harbor,MD,USA, 2014:1-5.

［10］邓威,李欣然,徐振华,等.考虑风速相关性的概率潮流计算及影响分析[J].电网技术,2012,36(4):45-50.

［11］熊强，陈维荣，张雪霞,等.考虑多风电场相关性的场景概率潮流计算[J].电网技术,2015,39(8):2154-2159.

［12］Narayan K S,Kumar A.Impact of wind correlation and load correlation on probabilistic load flow of radial dis⁃tribution systems[C]//IEEE International Conference on Signal Processing,Informatics,Communication and En⁃ergy Systems.Kozhikode India,2015:1-5.

［13］吴晨曦,文福拴,陈勇,等.含有风电与光伏发电以及电动汽车的电力系统概率潮流[J].电力自动化设备, 2013,33(10):8-15.

［14］Chen Y,Wen J,Cheng S.Probabilistic Load Flow Meth⁃od Based on Nataf Transformation and Latin Hypercube Sampling[J].IEEE Transactions on Sustainable Energy, 2013,4(2):294-301.

［15］李慧,孙宏斌,张芳,等.风电场风速分布模型研究综述[J].电工电能新技术,2014,33(8):62-66.

［16］Zhou X,Li J,Ma Y.Review on wind speed model re⁃search in wind power systems dynamic analysis[C]//In⁃ternational Conference on Sustainable Power Generation and Supply,2009.Supergen.Nanjing,China,2009:1-5.

［17］Weng Z X,Shi L B,Xu Z,et al.Effects of wind power variability and intermittency on power flow[C]//Power and Energy Society General Meeting.San Diego,CA, USA,2012:1-7.

［18］Ghofrani M,Arabali A,Etezadi-Amoli M,et al.Energy Storage Application for Performance Enhancement of Wind Integration[J].IEEE Transactions on Power Sys⁃tems,2013,28(4):4803-4811.

［19］黄海煜,于文娟.考虑风电出力概率分布的电力系统可靠性评估[J].电网技术,2013,37(9):2585-2591.

［20］Xiao Q.Evaluating correlation coefficient for Nataf trans⁃formation[J].Probabilistic Engineering Mechanics, 2014,37(4):1-6.

Probabilistic power flow algorithm of considering the correlations between wind speed and failure of wind turbines

YE Jiajun，WEI Huanzheng，LI Muxing
(School of Automation,Guangdong University of Technology,Guangzhou Guangdong 510006,China)

Aiming at the problem of the power system probabilistic load flow(PLF)analysis in view of indeterminacy and pertinency of wind speed and failure of wind turbine generators(WTG)when wind power integration,establishes wind farm power output model based on Nataf transform and considering the indeterminacy and pertinency of wind speeds and failure of WTG,puts forward a Monte Carlo PLF analysis method which can flexibly deal with the correlation between wind speed and WTG failure, and introduces the‘Latin hypercube sampling’method to improve sampling efficiency and decrease the computation complexity.The simulation result shows that the method can reflect the practical situation of the wind farm power output,rationally estimate the influence of wind power integration on PLF,helps to the wind farm site selection and power grid planning.

pertinency;Monte Carlo method;Nataf transform;probabilistic power flow;Latin hypercube sampling

TM614

A

1672-3643（2017）03-0025-07

10.3969/j.issn.1672-3643.2017.03.005

2017-03-28

叶嘉俊（1993），男，工学硕士，研究方向为综合能源系统分析与优化。

有效访问地址：http://dx.doi.org/10.3969/j.issn.1672-3643.2017.03.005