压裂车动力系统隔振优化研究
2017-08-16邱宗斌
邱宗斌
(川庆钻探工程公司 长庆井下技术作业公司,西安 710018)
压裂车动力系统隔振优化研究
邱宗斌
(川庆钻探工程公司 长庆井下技术作业公司,西安 710018)
针对石油压裂车柴油发动机和压裂泵等动力系统的振动问题,提出了一种隔振系统参数优化方法。该方法的优化目标为提高柴油发动机和压裂泵等动力系统的解耦率,依据线性规划理论方法中的多目标到达法以及解耦优化理论,并采用MATLAB自带的fgoalattain函数来优化隔振系统的参数,通过改变物理参数和悬置原件的结构来提高系统的隔振效果。最后,通过时域仿真对优化效果进行了验证。
压裂车;隔振;解耦率;优化
随着石油开采技术的快速发展,石油增产的压裂技术得到越来越广泛的关注[1-2]。压裂工作属于高压高负荷场景下的野外工作,需要配置专门的压裂车组,一般情况下,压裂车的工作环境十分恶劣,且工作的持续时间较长,为满足高压高负荷场景下的野外工作需求,对压裂车的性能也提出了较高的要求。而对压裂车的发动机和压裂泵而言,不仅自身具有较大的质量,且在进行压裂作业时会产生很大的激振,对压裂作业的工作环境会产生极大的影响[3-6]。
针对压裂车的发动机和压裂泵的振动问题,国内外学者也展开了一系列的研究,目前的研究主要集中在压裂车振动系统的数学建模,文献[7]利用Pro/E软件建立了压裂车三缸泵的三维实体模型,然后将多刚体的动力学软件ADAMS进行导入,建立了对应的虚拟样机模型;文献[8]采用状态空间法和集中参数法建立了平衡悬架、车台发动机以及压裂泵和车架的多体耦合动力学模型,并利用MA TLAB/Simulink软件对压裂车在作业执行过程中的刚度、转速和阻尼等参数进行了耦合振动仿真分析。上述研究对压裂车振动系统的数学模型有了一定的研究,如何优化压裂车的隔振系统却研究较少。因此,本文从实际工程最大化能量解耦角度出发,结合多目标到达法和解耦优化理论,采用振动系统的解耦率为隔振系统的优化目标,通过更改悬置原件的物理参数和原件结构来改善系统的隔振效果。
1 隔振优化原则
压裂车橡胶隔振器一般具有较低的固有频率带。在实际工程应用中,对压裂泵隔振系统和发动机悬置系统而言,难以实现两者的完全解耦。因此,解耦优化的对象主要专注于和系统激励紧密相关的自由度上。目前常用的激励惯性解耦理论主要包括能量解耦理论和打击中心理论。然而在石油压裂车工作场景下,由于有限的台上空间而致使布置十分紧凑,具有较高的空间利用率,又因为打击中心理论对布置方式的空间大小要求极高,该方法不适用与石油压裂车工作场景。故文中采用能量解耦法对系统的隔振进行优化。
能量解耦法中的能量解耦率是指从能量分布的视角求取不同阶模态下每个坐标占取的能量比例[9]。若系统在此阶的振动频率时,振动能量只分布于一自由度之下,则系统紧紧沿着次自由度进行振动,而和其他的自由度是解耦的。在多自由度系统下,不同自由度之间是存在相互耦合的关系的,而隔振系统的优化也就是激励作用下的不同自由度上的耦合振动解耦。
对隔振系统的整体性能而言,可从振动影响方面进行考虑分析。根据振动分析的基本理论,单自由度系统在振动情况下的振动周期为:
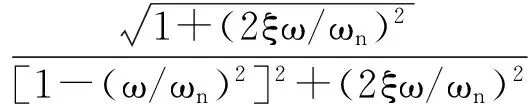
(1)
式中:ω是外部激励作用下的频率;ωn是系统固有的频率;ξ是系统的阻尼比;λ是系统的频率比。
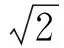
当压裂车工作在负荷稳定的情况下时,其对应的激励源主要为压裂泵和柴油发动机内部不平衡的力矩和惯性力,以及因其结构本身带来的力矩波动。振动系统具有的共振分布即是由这些激励的所有频率所构成,危险的共振区是在进行隔振优化时重点所需要考虑的区域。因此,从频率方面考虑可以将振动系统的激励源分为翻倒力矩激励和惯性力激励,两者所对应的频率分别为:
翻倒力矩的激励频率

(2)
式中:f1是翻倒力矩的激励频率;n是压裂泵和柴油发动机的转速;N是缸数;τ是冲击的数量,压裂泵冲击数量取值为2,柴油发动机的冲击数量取值为4。
惯性力的激励频率

(3)
式中:f2是惯性力的激励频率;Q是不同阶数下的激励比例系数,一阶激励的取值Q=1,二阶激励的取值Q=2。
2 发动机悬置系统优化
2.1 目标函数
针对发动机悬置系统,其在发动机曲轴坐标系下的xyz方向具有较为理想的解耦率,而在θy和θx方向上具有较强的耦合程度,表明该方向上的发动机激励的翻倒力矩较大,该自由度上的强耦合会很大程度上影响隔振系统的效果。因此将解耦率作为需要优化的量。选取的优化目标如下:
(4)
式中:max(Tpi)是第i阶数上的最大解耦率;βi是加权系数。
自由度上的不同需求可将加权系数进行调整,反复调整加权系数的取值即可得到理想的优化结果。采用MATLAB中的fgoalattain函数来解决该类优化问题[10],其对应的分析流程如图1所示。
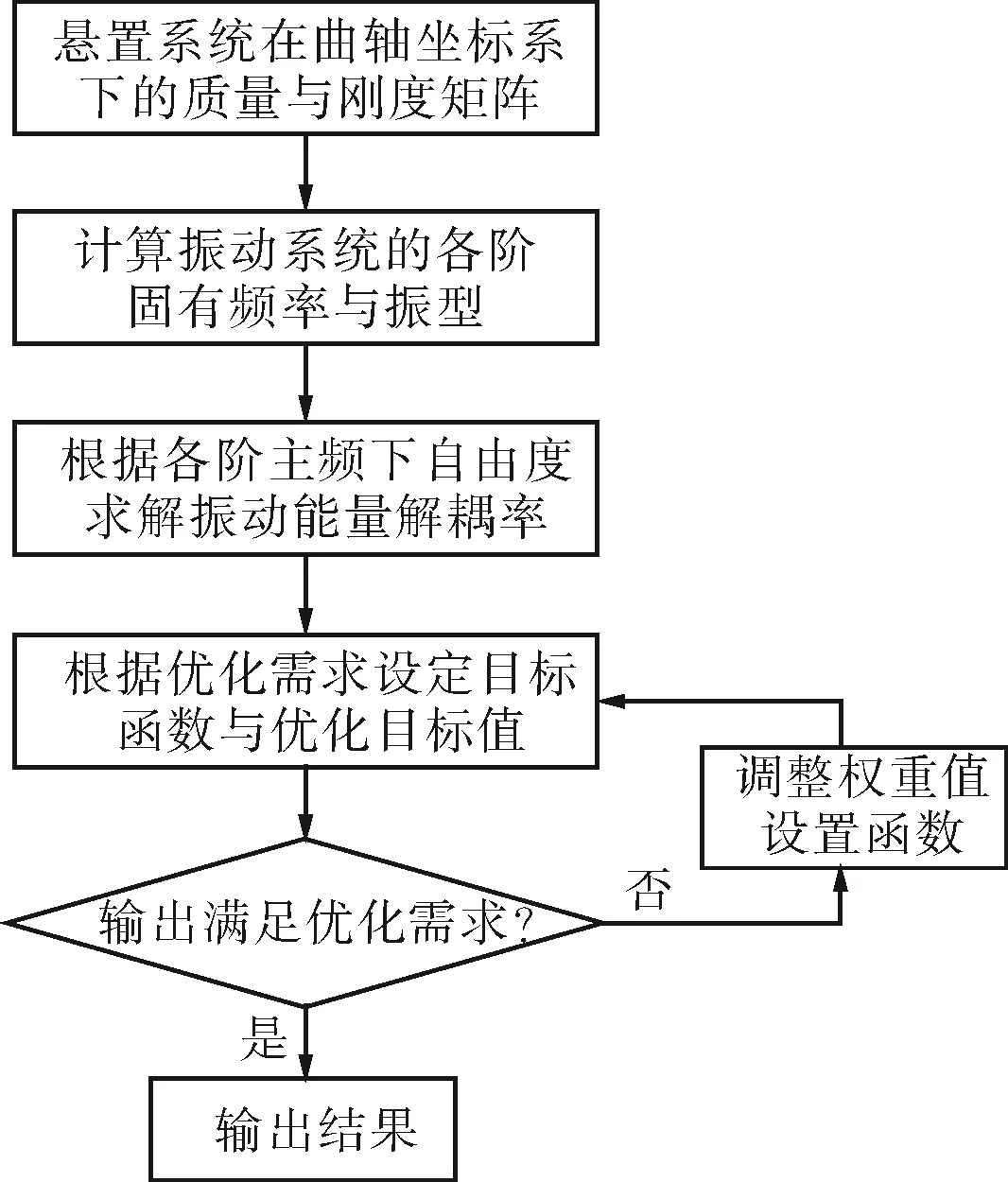
图1 MATLAB优化流程
2.2 优化约束条件
1) 解耦率和固有频率值分配。对于解耦率的目标取值方面,由于采用的悬置原件是橡胶悬置,因此希望优化后的解耦率目标取值至少能够达到80%左右。对于固有频率的分布,因为文中选取的发动机工作转速为800~2 000r/min,则可以求出系统的工作频率为93.3~266.7Hz。同时,发动机具有较宽的工作频率,根据式(1)~(3),发动机的固有频率和翻侧方向的频率应小于66Hz。
2) 悬置元件主轴刚度约束值。较低的主轴刚度会使振动的幅度增大,而增大主轴刚度虽然能够降低振动的幅度,但是会使悬置原件振动的传递率增大,进而降低了系统的隔振性能。考虑到工艺问题,通常将压减的刚度比值取3~8,该取值范围能够作为线性不等式的约束条件对,即刚度值和刚度比的约束。
2.3 优化结果
在Matlab软件中进行优化调节,能够获取比较合理的悬置系统的主轴刚度,如表1所示。表中,U、V、W是发动机悬置局部弹性主轴坐标系。
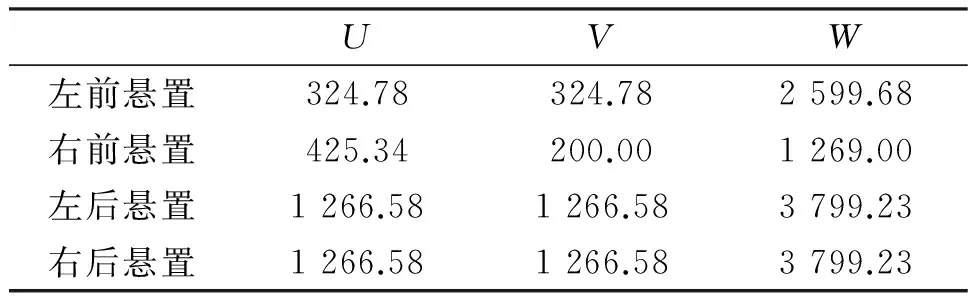
表1 优化后的悬置元件主轴刚度 N/mm
经过优化后的固有频率以及对应的解耦率分别如表2所示,其中,x、y、z是发动机曲轴坐标系,θx、θy、θz是绕x、y、z方向的转动坐标系。

表2 优化后的悬置系统固有频率和解耦率
根据优化后的振动特性可知,发动机悬置系统的振动分布能够在一定程度上得到有效的改善,每个自由度上都能满足其对应的要求。耦合模型的固有频率及其解耦率都能够满足要求。因此对发动机悬置系统的刚度进行优化具有一定的意义。
3 压裂泵隔振系统优化
3.1 目标函数
对压裂泵系统而言,同样的可选取优化目标如下:
(4)
式中:max(Tpi)是第i阶数上的最大解耦率;αi是加权系数。
同样的可根据自由度上的不同需求将加权系数进行调整,反复地调整加权系数的取值即可得到理想的优化结果。
3.2 优化约束条件
1) 解耦率和固有频率值分布。压裂泵常用的工作冲次是100~300min-1,即可以求出对应倾覆力矩的频率为8.33~25Hz。因此,压裂泵的侧翻和竖直方向的固有频率应不大于5.9Hz,该条件即可作为优化的约束条件。解耦率的约束条件同上述分析的发动机解耦率的约束条件是一致的。
2) 隔振系统主轴刚度的约束取值。同样的将压减的刚度比值取3~8,该值作为线性不等式的约束条件对刚度值和刚度比进行约束。
3.3 优化结果
同理,在Matlab软件中进行优化调节,能够获取比较合理的橡胶隔振系统的主轴刚度,如表3所示,其中P、Q、R是压裂泵隔振器局部弹性主轴坐标系。

表3 优化后的隔振元件主轴刚度 N/mm
隔振元件经过优化后的固有频率以及对应的解耦率分别如表4所示,其中x、y、z是压裂泵曲轴坐标系,θx、θy、θz是绕x、y、z方向的转动坐标系。
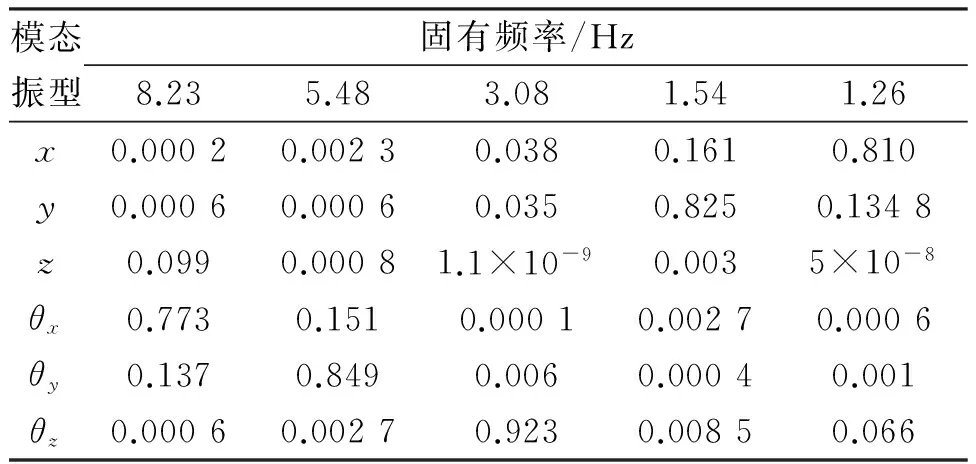
表4 优化后的隔振元件固有频率和解耦率
同理,通过优化之后,隔振元件系统的振动分布能够在一定程度上得到有效改善,每个自由度上都能满足其对应的要求。优化后的隔振元件固有频率及其解耦率都能够满足要求。因此对压裂泵隔振元件系统的刚度进行优化也具有一定的意义。
4 结论
本文对石油压裂车动力系统隔振进行了优化研究,优化的目标为提高柴油发动机和压裂泵的振动解耦率,根据能量解耦理论和多目标到达法,并采用MATLAB软件中的fgoalattain函数来优化隔振系统的参数。对隔振效果的优化进行了仿真验证,结果验证了优化结果的有效性。
[1] 程兴生,卢拥军,管保山,等.中石油压裂液技术现状与未来发展[J].石油钻采工艺,2014(1):1-5.
[2] 姜海洋.试论石油开发中体积压裂技术的应用[J].化工管理,2015(30):135-135.
[3] 桑猛.大功率压裂车车架承载能力研究[D].大连:大连理工大学,2013.
[4] 曹桐军,赵静,邱帅迪,等.悬置胶垫刚度变化对发动机隔振效率的影响研究[J].企业技术开发月刊,2016,35(16):43-45.
[5] 高媛,王红,单东升.2500型压裂车车架结构多目标拓扑优化设计[J].石油矿场机械,2015,44(5):49-53.
[6] 王红玲,单东升,高媛.压裂车车架结构尺度优化设计方法研究[J].石油矿场机械,2015,44(11):51-55.
[7] 马晓伟,刘健,孙延迪,等.基于ADAMS的压裂车三缸泵振动分析[J].机电工程,2014,31(11):1415-1418.
[8] 王川,谢真强,王国荣,等.压裂车作业过程耦合振动仿真分析[J].系统仿真学报,2016,28(7):1586-1592.
[9] 陈永瑞.基于Adams与Isight的轻卡动力总成悬置系统优化设计[D].青岛:青岛理工大学,2015.
[10] 张炜,李华.微机电系统微弹簧优化设计方法[J].探测与控制学报,2014(6):11-14.
Research on Vibration Isolation Optimization of Power System for Oil Fracturing Vehicle
QIU Zongbin
(Changqing Downhole Technical Service Company,CCDC,Xi'an 710018,China)
Aiming at the vibration problem of diesel engine and fracturing pump and other dynamic systems for oil fracturing vehicle,a parameter optimization method of vibration isolation system is proposed.The optimization goal of this method is to improve the decoupling rate of diesel engine and fracturing pump.According to the multi-objective arrival method and the decoupling optimization theory in the linear programming theory method,the fgoalattain function of MATLAB is used to optimize the parameters of the vibration isolation system,and the vibration isolation effect of the system is improved by changing the physical parameters and the structure of the originals.Finally,the optimization effect is verified by time domain simulation.
fracturing vehicle;vibration isolation;decoupling rate;optimization
1001-3482(2017)04-0065-04
2017-01-11
邱宗斌(1975-),男,甘肃泾川人,工程师,主要从事油田工程服务、试油压裂作业工作。
TE
A
10.3969/j.issn.1001-3482.2017.04.016
