星载GNSS-R准圆近似镜面反射点预测算法

杜璞玉，秦 瑾，周 勃

(上海航天电子技术研究所，上海 201109)

星载GNSS-R准圆近似镜面反射点预测算法

杜璞玉，秦 瑾，周 勃

(上海航天电子技术研究所，上海 201109)

利用GNSS反射信号进行遥感探测，已成为国内外遥感和导航技术领域研究热点之一。为满足星载GNSS-R对算法精度和效率的高要求，给出了一种新的准圆近似镜面反射点预测算法。介绍了该算法的基本思想和实现方法，仿真验证了准圆近似法的正确性，并就算法性能将其与现有的镜面反射点预测算法进行了仿真对比。仿真结果表明，准圆近似法具有精度高、运算速度快的优势，满足星载GNSS-R应用需求。

全球卫星导航系统反射信号；镜面反射点；准圆近似

0 引言

全球卫星导航系统(Global Navigation Satellite System，GNSS)所发射的高度稳定、可长期使用的L波段微波信号为中尺度的海洋遥感提供了新的信号源[1]。基于GNSS反射信号的遥感技术称为GNSS反射信号(GNSS-R)技术[2]。星载GNSS-R遥感技术具有覆盖范围广、观测周期短等特点[3]，已成为国内外遥感领域研究热点之一。

GNSS-R遥感器对反射信号处理时，镜面反射点被用作信号搜索和捕获的参考中心[4]，因此镜面反射点的精确定位在GNSS-R技术中具有重要意义[5]。

现有的镜面反射点预测算法都忽略了地球偏心率的影响，没有严格区分镜面反射点处的径向和法向[6]，计算出的镜面反射点位置与实际镜面反射点位置存在明显偏差。本文在充分研究现有算法的基础上，基于准圆近似思想，提出一种创新算法，详细介绍了该算法的思想及计算过程，并通过仿真对比说明，该算法精度高、收敛快，尤其适用于星载应用。

1 镜面反射点

1.1 定义

GNSS-R几何关系如图1所示。星载GNSS-R遥感器一般搭载在低轨卫星上，接收导航卫星直射信号的同时，接收来自地球表面具有明显反射作用的区域[7]，即闪耀区的反射信号。

图1 GNSS-R几何关系

定义闪耀区内，使得发射机—反射表面—接收机之间距离最短的地球上的点为镜面反射点，在反射信号处理过程中，一般将其作为信号搜索和捕获时确定估计的多普勒频移和近似码相位偏移的参考中心[8]。

1.2 镜面反射点应满足的条件

图2 镜面反射点处的几何关系

假设T、R、S的坐标分别为(Xt,Yt,Zt)、(Xr,Yr,Zr)、(X,Y,Z)，则当S为镜面反射点时，有以下关系：

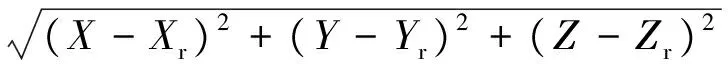
(1)

由镜面反射点的定义知道，镜面反射点为地球表面上到发射机和接收机距离和最短的点。假设参考椭球方程为：

(2)

构造拉格朗日函数：

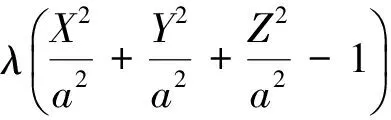
(3)

式(3)两端分别同时对X、Y、Z求偏导，并令3个偏导数都为0，有

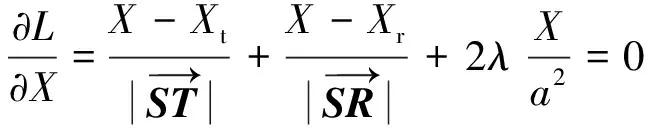
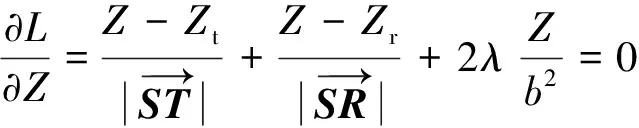
(4)

将式(4)的三式相加并移相，有

(5)

式中，第1项为镜面反射点到发射机的单位向量；第2项为镜面反射点到接收机的单位向量；等式右边为一个与镜面反射点处法向量共线的向量。式(5)说明，入射角等于反射角，即

αr=αt。

(6)

由此可以得出结论，镜面反射点满足菲涅尔反射条件[9]。一般在计算镜面反射点位置的迭代过程中，正是利用这一条件作为判断依据[10]。但值得注意的是，该条件只是一个必要条件，而非充分条件，因此在利用该条件计算出镜面反射点的位置后，还需要进一步验证计算所得点确实满足到发射机和接收机距离和最小这一定义。

2 镜面反射点位置的确定

2.1 现有算法及其不足之处

现有的镜面反射点预测算法主要有Gleason算法[11]、S.C.Wu算法[12]和线段二分法算法[13]等。

Gleason算法基于向量共线思想实现镜面反射点位置的预测，主要缺点为收敛速度慢，运算时间长[14]。

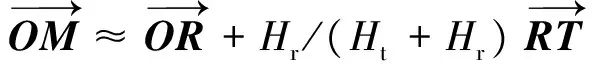
基于线段二分法算法与S.C.Wu算法的不同点主要体现在M点的搜寻方式上。该算法利用的基本思想类似于二分法求解方程过零点解的思想，通过对线段RT不断进行二分来寻找满足条件的M点。

然而通过分析不难发现，S.C.Wu算法和线段二分法算法在进行入射角/反射角的计算时，都是以S处的径向OM为基准的，而地球实际上为椭球，除了在赤道和2个极点位置处，地面上任意一点的法向和径向都不重合[16]，在此条件下计算出来的镜面反射点位置必然与实际镜面反射点位置存在偏差，为后续反射信号处理及高度反演引入误差[17]。

2.2 准圆近似算法

为了能够严格区分镜面反射点处的径向和法向，使算法真正适用于地球椭球模型，本文提出了准圆近似法算法来计算镜面反射点位置。算法思想如图3所示，首先假想一个与地球同心的半径为1的单位球体，将整个地球及WGS-84系下的接收机R和导航卫星T的位置都映射到该单位球体对应的直角坐标系下，记为R′、T′。在新的坐标系中计算R′、T′在单位球体上的镜面反射点S′，最后将S′映射回WGS-84坐标系，即为所要求的镜面反射点S。由于球体上任一点处径向和法向重合，因此由R′、T′求解S′的过程可以采用线段二分法。

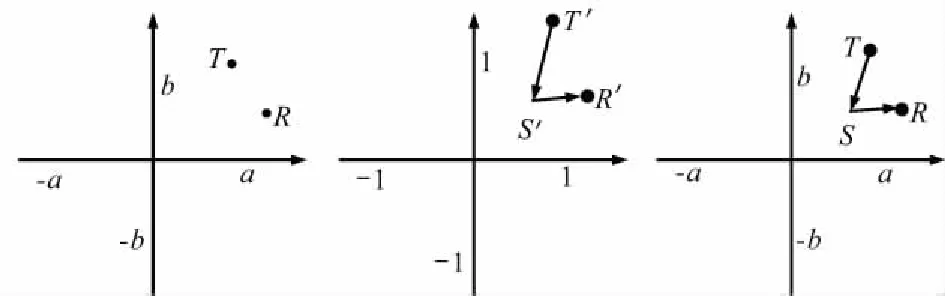
图3 准圆近似算法思想

由椭球到单位圆球的映射矩阵可以表示为：

(7)

式中，a、b分别为WGS-84地球椭球模型的半长轴、半短轴。则有如下的坐标映射关系：

R′=FR；

(8)

T′=FT；

(9)

S=F-1S′。

(10)

3 算法验证及对比分析

3.1 算法正确性验证

通过Matlab对准圆近似法进行了仿真。接收机和发射机位置信息由STK软件提供，发射机为GPS卫星，接收机设置为低轨卫星，圆形轨道，轨道倾角80°，轨道高度800 km，仿真精度设置为10-5。

首先对某一时刻的静态情形进行了仿真，选取导航卫星、接收机坐标分别为：

T(-3 371 858.561，-25 160 382.591，7 481 783.308)，

R(-3 307 925.703，-6 232 921.467，786 331.692)，

由准圆近似法计算此时镜面反射点的位置为：

S( -2 723 191.829 147 94，-5 704 040.021 235 89，

850 826.964 145 598)。

由于菲涅尔反射条件只是镜面反射点的必要条件，因此有必要对上述计算得到的反射点位置是否满足镜面反射点的定义进行验证。验证方法：由算法可以得到S点的WGS-84坐标和纬度、经度和高度信息，以S点为中心，设置经纬度范围为[-5°，5°]，以0.01°为步长，取得1 001个样本点，分别计算导航卫星T和接收机R到这些点的距离和。若S点确实为镜面反射点，则S点处对应的距离和应取得最小值，仿真结果如图4所示。

图4 准圆近似算法验证

从图4中可以看出，仿真结果呈现出碗状，且最低点的纬经高坐标为(7.707 5，-115.520 4，0)，由准圆近似法计算得到的S点纬经高坐标为(7.707 2，-115.520 5，0)，二者距离差为29.87 m。考虑到天线波束宽度及天线足印范围(约为70 km)，该误差在中尺度海洋测高应用中不会对测量结果产生影响，可以认为由准圆近似法计算得到的点，即为所求镜面反射点。

3.2 算法对比分析

静态情形下，对Gleason算法、S.C.Wu算法、线段二分法算法和准圆近似法进行了对比仿真。接收机和发射机位置与3.1节中的相同，分别利用4种算法计算出镜点在地表的位置，并从收敛次数和计算时间等方面对4种算法进行了对比，结果如表1所示。

表1 算法性能对比

由表1可以看出，Gleason算法的收敛速度最慢，迭代次数和运算时间与其他3种算法相比差了2个数量级。另外3种算法的运算时间都只有ms级，符合星载应用对算法计算速度的要求。值得一提的是，准圆近似法中虽然使用了线段二分法计算S′，且多了坐标映射的步骤，但其迭代次数和运算时间都要优于线段二分法，相比其他算法，该算法具有明显优越性。

动态情形下，取仿真场景时间为2014年12月23日02:15:00.000～02:45:00.000，每隔60 s读取一次导航卫星和接收机的位置信息，分别使用4种算法计算镜面反射点的位置，以准圆近似法的计算结果为基准，计算其他3种算法得到的镜面反射点位置到S的距离。仿真结果如图5所示，各采样点时刻对应的卫星高度角如图6所示。

图5 不同算法相对于准圆近似法的距离差

图6 采样点时刻的卫星高度角

从图5和图6可以发现，S.C.Wu算法的计算结果与其他算法结果偏离较大，原因为S.C.Wu算法完全依赖于地球圆球模型，计算中多次用到地球半径，且这里的计算结果没有经过修正。Gleason算法和线段二分法算法的结果几乎一致，且在卫星高度角较低时与准圆近似法结果之间的差值较大，在卫星高度角较高时与准圆近似法结果之间的差值较小。为实现高精度海面测高，一般优先选择高度角高(≥60°)的卫星进行测量，在这样的条件限定下，Gleason算法、线段二分法等算法与准圆近似法结果之间的距离差小于一个C/A码片对应的距离(293 m)。当GNSS-R遥感器在地面应用时，这一误差对测高精度不会造成很大的影响，地球可看作圆球，在不区分的径向与法向的情况下，也能够保证计算得到的镜面反射点的位置精度。但在星载GNSS-R任务中，对镜面反射点位置有高精度的要求，此时就不能忽略实际地球作为一个椭球体，其偏心率所带来的影响。再考虑到在计算速度上的优越性，准圆近似法算法具有更好的适用性。

3.3 结论

由上述仿真可以得出如下结论：

① 使用准圆近似法计算得到的反射点，基本满足在以其为中心的一定区域内从该点到导航卫星和GNSS-R接收机的距离和最短的条件，即该反射点即为所要找的镜面反射点；

② 准圆近似法的精度极高，与理论镜面反射点只存在几十米的误差，考虑到天线波束宽度及天线足印范围，该误差在中尺度海洋测高应用中不会对测量结果产生影响；

③ 在算法效率方面，准圆近似法迭代次数少、运算速度快，相比现有的镜面反射点预测算法，具有明显优势，尤其适用于星载GNSS-R应用。

4 结束语

针对星载GNSS-R微波遥感探测任务，本文提出了一种新的镜面反射点预测算法，即准圆近似法，该算法在计算镜面反射点时严格区分了地球椭球模型的径向与法向，克服了传统镜面反射点预测算法的不足之处。仿真分析表明，通过准圆近似法求出的反射点的位置与理论镜面反射点位置误差极小，具有较高精度。与现有其他算法的对比分析也表明，该算法在运算效率方面也有明显优势，尤其适用于星载GNSS-R任务。

[1] 李伟强.面向遥感应用的GNSS反射信号接收处理方法研究[D].北京:北京航空航天大学,2011.

[2] 李颖,朱雪瑗,曹妍,等.GNSS-R海洋遥感监测技术综述[J].海洋通报,2015(2):121-129.

[3] 李紫薇.GNSS海洋微波遥感技术与应用进展[C]∥微波遥感技术研讨会论文集,2006:75-79.

[4] GLEASON S,GEBRE-GIABHER D.GNSS应用与方法[M].杨东凯,樊江滨,译.北京:电子工业出版社,2011.

[5] 马小东,张凤元,杨东凯,等.星载GNSS海面散射信号功率分析与接收方法研究[C]∥第六届全国信号和智能信息处理与应用学术会议论文集,2012:199-202.

[6] MARTIN-NEIRA M.A Passive Reflectometry and Interferometry System(PARIS):Application to Ocean Altimetry[J].Esa Journal,1993,17(4):331-355.

[7] HALL C D,CORDEY R A.Multistatic Scatterometry[C]∥Geoscience and Remote Sensing Symposium,1988.IGARSS ′88.Remote Sensing:Moving Toward the 21st Century,International.IEEE,1988:561-562.

[8] 张帅,杨东凯,李伟强.GNSS反射信号同步影响因素分析[C]∥第六届全国信号和智能信息处理与应用学术会议论文集,2012:162-165.

[9] 胡长江,李英冰.全球导航卫星反射信号的镜面反射点算法[J].测绘科学,2014,39(12):33-35.

[10] GLEASON S,GEBRE-GIABHER D.GNSS应用与方法[M].北京:电子工业出版社,2011.

[11] GLEASON S,HODGART S,SUN Y,et al.Detection and Processing of Bistatically Reflected GPS Signals From Low Earth Orbit for Purpose of Ocean Remote Sensing[J].IEEE Trans Geosciences and Remote Sensing,2005,43(6):1 229-1 239.

[12] WU S C,MEEHAN T,YOUNG L.The Potential Use of GPS Signals as Ocean Altimetry Observable[C]∥National Technical Meeting,Santa Monica,CA,1997:463-450.

[13] 张波,王峰,杨东凯.基于线段二分法的GNSS-R镜面反射点估计算法[J].全球定位系统,2013(5):11-16.

[14] PARK H,CAMPS A,VALENCIA E,et al.Retracking Considerations in Spaceborne GNSS-R Altimetry[J].Gps Solutions,2012,16(4):507-518.

[15] 张益强.基于GNSS 反射信号的海洋微波遥感技术[D].北京:北京航空航天大学,2008.

[16] RIUSA,CARDELLACH E,MARTIN-NEIRA M.Altimetric Analysis of the Sea-Surface GPS-Reflected Signals[J].IEEE Transactions on Geoscience & Remote Sensing,2010,48(4):2 119-2 127.

[17] MARCHAN-HERNANDEZ J F,CAMPS A,RODRIGUEZ-ALVAREZ N,et al.An Efficient Algorithm to the Simulation of Delay-Doppler Maps of Reflected Global Navigation Satellite System Signals[J].Geoscience & Remote Sensing IEEE Transactions on,2009,47(8):2 733-2 740.

Quasi-spherical Approximation Specular Searching Method for Space-borne GNSS-R

DU Pu-yu,QIN Jin,ZHOU Bo

(ShanghaiAerospaceElectronicTechnologyInstitute,Shanghai201109,China)

The Global Navigation Satellite Systems-Reflectometry(GNSS-R) is a remote sensing technique which has been acquiring increasingly high interest in recent years.A new method called quasi-spherical approximation to predict the position of specular points is proposed in this paper to satisfy the high precision and efficiency requirements in space-borne GNSS-R missions.The principle and implementation of the method are introduced,and the accuracy of the result is validated by simulation.By comparing quasi-spherical approximation with traditional specular searching algorisms,it is proved that the new method is more accurate and efficient for space-borne GNSS-R missions.

GNSS-R;specular point;quasi-spherical approximation

10.3969/j.issn.1003-3106.2017.09.10

杜璞玉,秦 瑾,周 勃.星载GNSS-R准圆近似镜面反射点预测算法[J].无线电工程,2017,47(9):51-54，82.[DU Puyu,QIN Jin,ZHOU Bo.Quasi-spherical Approximation Specular Searching Method for Space-borne GNSS-R[J].Radio Engineering,2017,47(9):51-54，82.]

S973.1+1

A

1003-3106(2017)09-0051-04

2017-03-31

上海市科学技术委员会科研计划基金资助项目(14DZ1110300)。

杜璞玉 男，(1991—)，硕士，工程师。主要研究方向：GNSS-R算法研究与总体设计。

周 勃 男，(1979—)，硕士，高级工程师。主要研究方向：GNSS-R总体设计。