圆周率在中国的发展①
2017-08-16郝秀惠房元霞
郝秀惠 房元霞
(聊城大学数学科学学院,山东聊城252059)
圆周率在中国的发展①
郝秀惠 房元霞
(聊城大学数学科学学院,山东聊城252059)
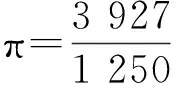
圆周率,几何算法,刘徽,计算机
圆周率π表示圆的周长与直径的比值,自有文字记载开始,它就成为了经久不衰的话题.德国数学史家康托(Contor Georg,1845-1918年)曾说:“历史上一个国家所算的圆周率的准确程度,可以作为衡量这个国家当时数学发展水平的指标.”在中国历史上,圆周率作为一个系统的数学领域是处于时代前沿的,它的计算方法也比较领先.根据圆周率在中国历史上的发展过程,我们可以将它的发展阶段分为:试验获取阶段、几何算法阶段、计算机时代.
在中国,圆周率的历史要追溯到最早的古算书《周髀算经》,这本书在周公与商高的问答中有所记载.另外,在《周礼考工记》中也有相同的记载.一直到《九章算术》中的方田、商功、少广各章中凡是圆或圆的面积、圆柱、圆锥,用到周径之比,都取π=3.秦汉之前皆取π=3,后人称之为“古率”.古率的误差很大,随着社会的进步,人们开始进一步精确圆周率值.公元9年,西汉的刘歆为王莽造律嘉量斛,成为第一个改正古率的人.
在实验获取阶段,人们是利用一些常用的刻度尺和其他的测量工具,或自制的圆来探索圆周率的,还处于圆周率探索初期,它的计算方法和测量工具相对来说都不是很科学.但是,他们的探索为以后科学家对圆周率的研究提供了一定的理论依据.
通过测量和推算所得到的圆周率是粗略的,随着时间的推移,以及中国数学家的不懈努力,关于圆周率的计算过度到几何算法阶段.在中国历史上,我们可以通过几位数学科学家根据历史脉络来研究圆周率的推算过程.从张衡到刘徽,再到祖冲之,他们在历史上不仅代表了某个历史时期的数学发展状况,还犹如历史长河中的一条彩色绸带,将圆周率的发展历程连接起来.
1 张衡与圆周率

关于张衡对圆周率所做工作,在他之后的刘徽做过相关介绍,由刘徽的介绍,我们可以了解到张衡做了下列工作:

第三,“衡又言,质六十四之面,浑二十五之面,质复言浑,谓居质八分之五也.”这是说,立方体:内接球(质:浑)=8∶5(这是错误的).
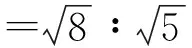

根据刘徽对张衡工作的介绍与评价,我们不难看出,张衡除了出发点丸柱率有误外,他的整个推导过程都是正确与精彩的.张衡对圆周率的研究,即便是在证明过程中存在错误,但他的思路和方法在当时也是先进的,在一定意义上开辟了一个新方向,为后人在圆周率方面的研究提供了依据和重要思路.
2 刘徽与圆周率
刘徽(225-295)是我国魏晋时期著名数学家,他把机械方法和极限思想应用于近似计算,在中国第一次提出求圆周率近似值的科学方法,创立了以几何学求圆周率的方法,开创了中国数学之新纪元.

图1 圆内接正六边形割圆

刘徽在求圆周率数值的过程,可以说是数学原理加上非理性因素双重作用的结果.但对后来祖冲之对圆周率的研究做了进一步的铺垫和引导.
3 祖冲之与圆周率
祖冲之(429-500年),我国古代杰出的数学家、天文学家和机械制造家.他在圆周率上的贡献是:利用算筹进行开方运算,将圆周率精确到小数点后7位.
祖冲之曾经写过一本著作《缀术》,记录了他对圆周率的研究过程和成果,但当时由于不受官学重视,后来失传.因此,在2008年出版的《科技导报》上,将“祖冲之究竟是怎样计算出圆周率 值的?”列为公众关注的未解科学难题之一,下面讨论的也仅为各位数学家关于祖率的合理猜想.
根据推测,在前人刘徽工作的基础上,祖冲之意识到可以通过增加割圆次数,提高圆周率的精度.但是π的精度不会超过边长的有效数字,而有效数字随着边长的不断增加而减小,或许这就是刘徽计算圆周率精度受到的理论限制.虽然史书上没有他推算圆周率的过程,但根据《隋书·律历志》:“古之九数,圆周率三,圆径率一,其术疏舛.自刘歆、张衡、皮延宗之徒,各设新率,未臻折衷.宋末,南徐州从事史祖冲之更开密法,以圆径一亿为一丈,圆周盈数三丈一尺四寸一分五厘九毫二秒七忽;肭数三丈一尺四寸一分五厘九毫二秒六忽,正数在盈肭二限之间.密率:圆径一百一十三,圆周三百五十五.约率:圆径七,周二十二.”我们可以得知:祖冲之求得3.141 592 6<π<3.141 592 7,密率:π=355/113(3.141 592 9),约率:π=22/7(3.142).据推测,祖冲之仍是按照刘徽的割圆术来进行推算的.他采用和刘徽相仿的方法,计算出S12 288=3.14 159 251方丈,S24 576=3.14 159 261方丈.代入刘徽不等式S2n 要得到这一精确度的结果,需要对9位数字的数进行130次以上的各种运算.在祖冲之时代,由于还没有应用小数,因而在实际计算中常用分数来表示圆周率,这在工作量上无疑是一个大工程.因此,用密率355/113表示π的近似值,是一项伟大的贡献.为此,传到日本后,日本数学史家三上一夫1913年建议将祖冲之圆周率的密率数值命名为“祖率”,得到大家的一直赞同.祖冲之关于圆周率的探索,超过了世界水平1 000多年,在张景中《数学家的眼光》一书中指出:祖率与 的精确值误差不超过0.000 000 267,这无疑是祖率的精妙和伟大之处. 近代以来,随着中西方的频繁交流,关于圆周率的计算方法和思想得到进一步的融合和发展.经过几千年的历史,关于圆周率的计算仍未停止,尤其是计算机的出现,使得计算圆周率的脚步不断加快,90年代初,新的计算方法已经计算到圆周率的值达到4.8亿位.为了纪念我国古代数学家对圆周率的研究,国际数学学会于2011年正式宣布,将每年的3月14日设为国际数学节,即“国际圆周率日”. 然而,我们都很清楚,圆周率是一个“无限不循环小数”,而且还是一个超越数.数学家之所以仍然对此继续做相关研究,除了因为他们的好奇心或领先于人的心态在作怪,更重要的原因是,圆周率在生活中的巨大意义.因此,计算机时代的我们对于圆周率的关注,更倾向于它在生活中的应用. 如,锻炼记忆方面:在节目《走近科学》中,来自海南的七旬老人在脑梗发作之后,经过几年的自我脑力训练,将圆周率背诵到6 000多位.对于老人,神经元在凋亡,记忆也在衰退,但他记忆圆周率的过程却成了他锻炼记忆的过程;检验计算机性能:在π计算的公式、时间等完全相同的条件下,如果甲机比乙机能计算出更多位的π值,则甲机性能好;借助计算机检验数学公式的优劣:一台计算机在相同的条件下,先后用不同的公式计算π到相同多的位数,用时少的那个公式更优越;另外,圆周率的计算也为科学计算提供了很多信息,比如误差的正负、大小,以及算法的加速等. 我们也不要过分夸大它对记忆力的训练功能.2005年11月20日,西北农林科技大学理学院应用化学专业在读硕士生吕超成功创造了“背诵圆周率”吉尼斯世界新纪录.在背诵圆周率的吉尼斯纪录历史上,第一次留下了中国人的名字《华商报》.但是,他付出了很大的代价和时间.这种锲而不舍的精神值得我们称颂,一个大学生背诵圆周率到9万位,对他的生活和身心素质有什么影响呢?计算机时代的青年人完全可以利用背诵圆周率的时间学到更多的东西. 圆周率是一个神秘的数,随着社会和科技的发展,以及人们对它的进一步研究,这个奇迹般的数将会出现在更多的领域里,有关它的计算和计算方法也将会得到进一步发展,其应用领域也会越来越多.当然,我们也要正确运用圆周率,使其促进当今科学与生活的进步. [1] 强春晨,刘兴祥,岳育英.圆周率计算方法发展史[J].延安大学学报:自然科学版,2012(2):42. [3] 莫绍揆.论张衡的圆周率[J].西北大学学报:自然科学版,1996(26):359. [4] 切洛.刘徽与“割圆术”[J].青海师范大学民族师范学院学报,2008(1):68. [5] 朱一文.从“以率消息”看刘徽圆周率的产生过程[J].自然科学史研究,2008(1):59-70. [6] 魏徽.隋书.律历志卷十六[M].山海:上海古籍出版社,1986. [7] 张惠民.祖冲之家族的天文历算研究及其贡献[J].陕西师范大学学报:自然科学版,2002(4):29. [8] 王振东,姜楠.祖冲之与圆周率[J].力学与实践,2015(3):405. [9] 杨楠,豆战锋,刘兴祥.圆周率在社会生活中的应用[J].延安大学学报:自然科学版,2010(4):41. The Development of PI Algorithm in China HAO Xiu-hui FANG Yuan-xia (School of Mathematical Sciences,Liaocheng University,Liaocheng 252059,China) PI algorithm,geometry,Liu Hui,computer 2017-02-19 山东省本科高校教学改革项目(2005M054)资助 房元霞,E-mail:fangyuanxia@lcu.edu.cn. O632.0 A 1672-6634(2017)02-0020-044 圆周率的近代发展
5 总结

