最大熵方法在计算二维不变测度中的应用

张 茹，徐春伟，靳聪明

(浙江理工大学理学院，杭州 310018)



最大熵方法在计算二维不变测度中的应用

张 茹，徐春伟，靳聪明

(浙江理工大学理学院，杭州 310018)

在最大熵方法中采用三角单元上的分片线性基函数作为矩函数，用于二维映射的不变测度计算。有限元单元上分片线性基函数有局部支集和单位分割性质，因此最大熵方法得到的非线性方程组的Jacobi矩阵是正定的带状矩阵，保证了非线性方程组解的唯一性和稳定性。文中从理论上给出该方法的收敛阶，并且数值实验结果与理论一致。

有限元单元；不变测度；分片线性基函数；最大熵

0 引 言

很多科学和工程问题，都可以归纳为对离散动力系统渐近性质的研究。例如在分子动力学模拟[1]中可得到每个原子任意时刻的位置和速度，但原子的运动轨迹和速度是杂乱无章的，只有通过统计平均才能有效预测分子的温度、压力等热力学性质和结构性质。映射的不变测度[2]反映了动力系统的统计性质,因此对映射不变测度的研究非常重要。

假设映射S具有绝对连续不变测度，它的密度函数是映射S对应的Frobenius-Perron算子的不动点。关于不变密度的计算，Ulam[3]首先提出了分片常数逼近法，Ding等[4]提出了分片线性Markov方法，Boyarsky等[5]利用Markov变化将不变密度问题等价为一个矩阵特征值问题。最大熵方法由Jaynes[6]首先提出，已广泛应用于物理、化学、生物等领域,如一维映射的不变测度计算[7-8]、物种分布分析[9]、Fredholm积分方程求解[10-11]、化学反应能量依赖关系分析[12]、图像处理[13-14]、光谱分析[15]等。在传统的最大熵方法中，用标准单项基底1,x,x2,…,xn作为矩函数，会产生病态非线性方程组。近年来，对一维映射的不变测度计算，Ding等[8]提出了基于分片线性基函数的最大熵方法。这种方法克服了产生病态方程组的缺陷，理论和数值结果表明该方法收敛。

高维映射的不变测度可用于研究分子构象变化[1]等问题。本文基于有限元方法中的三角元上的分片线性基函数，用最大熵方法计算二维映射的不变测度。分片线性基函数满足单位分割性质和支集性质，因此由最大熵方法得到的非线性方程组的Jacobi矩阵是正定的带状矩阵。该方法简化了非线性方程组的计算，保证了解的唯一性和稳定性。

1 基于分片线性基函数的最大熵方法

1.1 不变测度及最大熵原理

定义1[16]设(X,∑,μ)是一个有限测度空间，可测映射S:X→X为非奇异变换，即由μ(S-1(B))=0，有μ(B)=0。若对于所有的B∈∑，有μ(S-1(B))=μ(B)，则μ是S的不变测度。

定义2[16]令(X,∑,μ)为一个测度空间，可测变换S:X→X是非奇异变换。由公式

定义的算子Ps:L1(X)→L1(X)称为对应于S的Frobenius-Perron(F-P)算子。

定理1[16]令Ps是可测变换S的F-P算子，并且f∈L1。则对于绝对连续有限测度

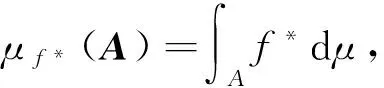
在S下不变，当且仅当f*是Ps的一个不动点。

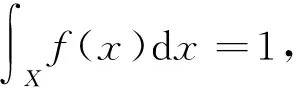
(1)

其中，当f(x)=0时，有flnf=0。

对于密度函数f(x)，若矩

(2)

已知gi(i=1,…,n)是矩函数，密度函数f(x)的解并不唯一。考虑如下约束优化问题：

i=1,…,n}

(3)

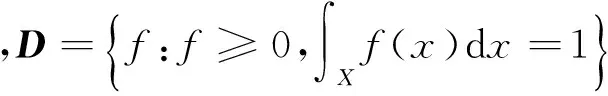
命题1[16]约束优化问题(3)的解为：

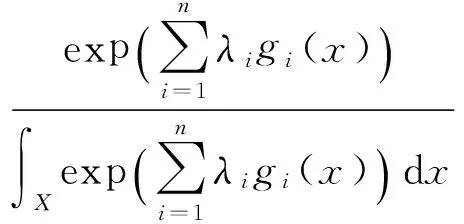
(4)

其中，λi(i=1,…,n)满足

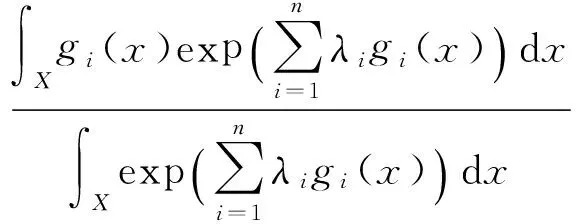
(5)

1.2 二维映射不变测度的计算

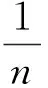
其中,

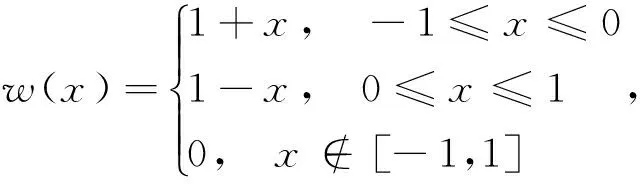
对任意(x,y)∈X，基函数{φi,j(x,y)}满足单位分割性质，即：

(6)

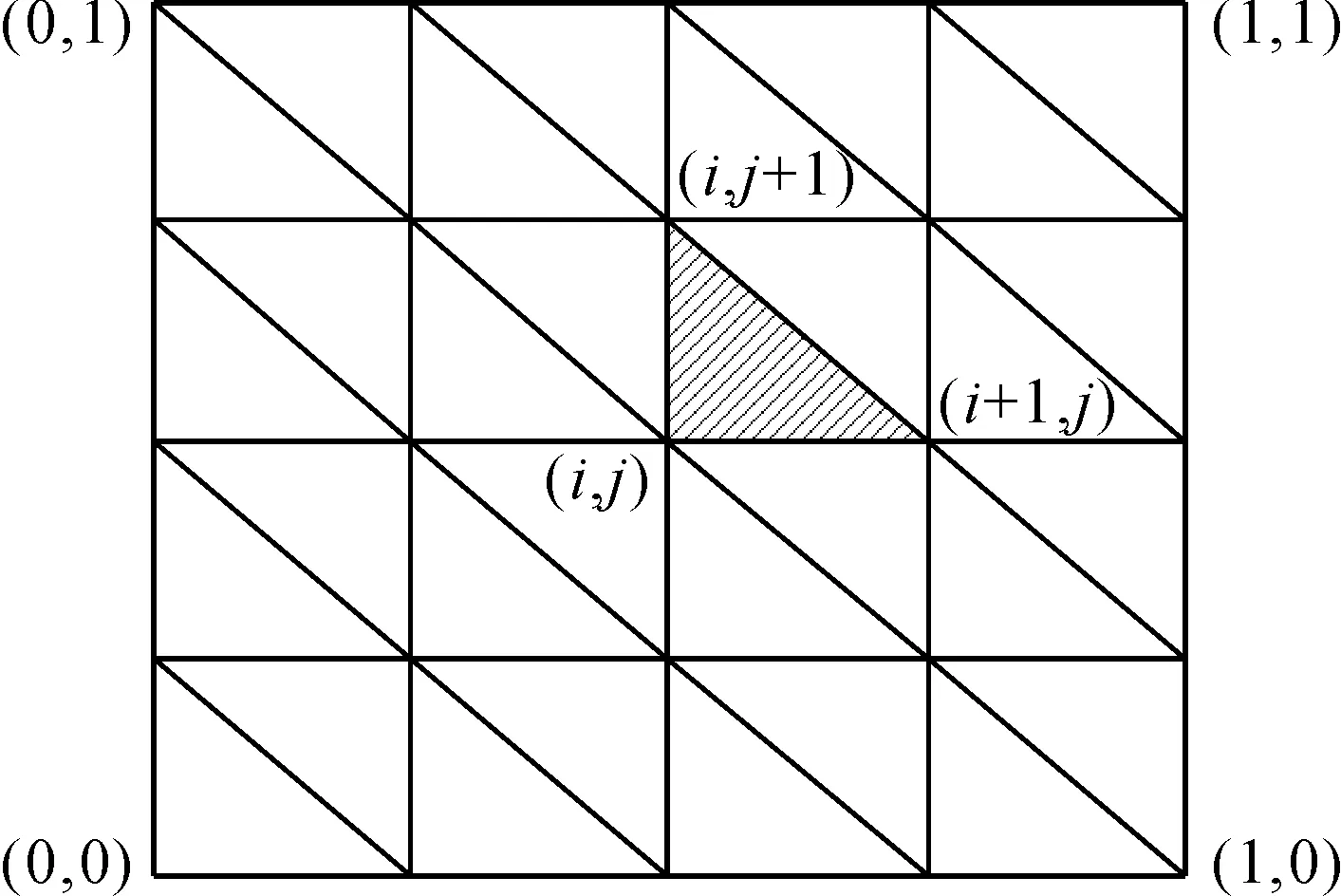
图1 X的三角剖分

在最大熵方法中，选择φi,j(x,y),(i,j=0,1,…,n)为矩函数，则矩为

mij=∬Xf*(x,y)φi,j(x,y)dxdy=∬suppφi,j(x,y)f*(x,y)φi,j(x,y)dxdy

(7)

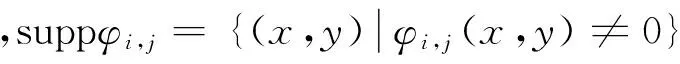
(8)

由式(8)可得命题2。

命题2 若f∈L1(X)是一个非负函数，且满足

∬Xf(x,y)φi,j(x,y)dxdy=mij,i,j=0,1,2,…,n

(9)

则f是概率密度，即∬Xf(x,y)dxdy=1。

证明：由式(6)和式(8)知，

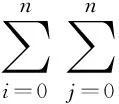
由命题2和最大熵方法知，若λi,j(i,j=0,1,…,n)满足

=mij,i,j=0,1,…,n

(10)

则

(11)

是近似不变测度。这里原最大熵方法式(5)简化为式(10)，基函数的单位分割性质使计算变得简单。

对于方程(10)的求解，考虑等式左边，则有

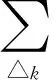
(12)

△k的一个顶点为(xi,yj)。在本文的三角剖分中，可能存在两种情况：

=∬△kφs(x,y)exp(λi,jφi,j(x,y)+λi+1,jφi+1,j(x,y)+

λi,j+1φi,j+1(x,y))dxdy

(13)

其中s取下标(i,j),(i+1,j),(i,j+1)；或者

=∬△kφs(x,y)exp(λi,jφi,j(x,y)+

λi-1,jφi-1,j(x,y)+λi,j-1φi,j-1(x,y))dxdy

(14)

其中s取下标(i,j),(i-1,j),(i,j-1)，(i,j)，是三角形△k的直角顶点。此积分可用数值积分方法计算，得到一个关于λi,j(i,j=0,1,2,…,n)的非线性方程组。

红色节日其背后是许多影响历史的关键节点和历史事件的原型，它犹如红色文化中的颗颗珍珠，串起我党红色历史与红色文化。通过在这些节日举办的各种纪念活动，可以让大学生重温红色历史，加深对中国共产党的理解与情感，因此可以以制度化的形式来推进这些红色节日，以促进和弘扬红色文化的传承。

若X∈R2被分割成任意三角形单元，假设任意三角形单元的顶点分别是(xi,yi),(xj,yj),(xk,yk)，如图2。采用有限元方法中的坐标变换

0≤ξ,η≤1

(15)

则任意三角形单元就可以转换为标准三角形单元(如图3)，其顶点关系为：

(xi,yi)↔(0,0)，(xj,yj)↔(1,0)，

(xk,yk)↔(0,1).

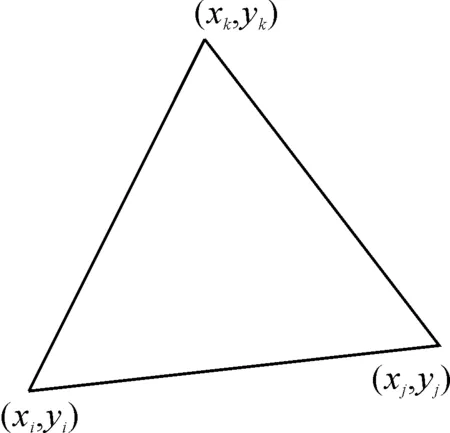
图2 任意三角形单元

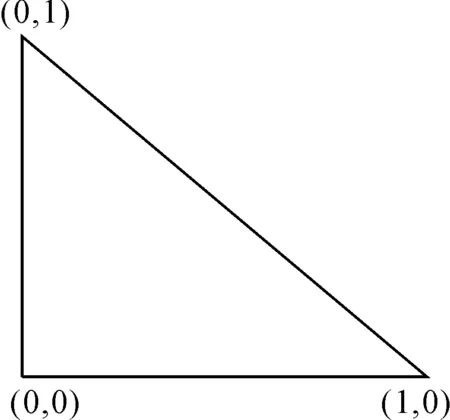
图3 标准三角形单元

考虑标准三角形单元上的积分，顶点(0,0),(0,1),(1,0)对应的分片线性基函数分别表示为

(16)

那么三角形△k上的积分可以表示为：

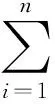
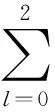
(17)

=(xj-xi)(yk-yi)-(xk-xi)(yj-yi)

(18)

利用数值积分可以得到关于λi,j(i,j=0,1,2,…,n)的非线性方程组(10)，可以用牛顿法或拟牛顿法迭代求解。

令G:R(n+1)2→R(n+1)2，它的元素定义为：

Gij(λ0,0,λ0,1,…,λn,n)=∬Xφi,j(x,y)

(19)

其中，i,j=0,1,2,…,n.则方程组(10)可以写为

Gij(λ0,0,λ0,1,…,λn,n)=0

(20)

G的Jacobi矩阵

φm,l(x,y)dxdy

(21)

其中，i,j,m,l均从0,1,…,n取值。与一维问题类似，很容易证明该Jacobi矩阵是正定的，由于φi,j(x,y)只在以(xi,yj)为顶点的三角形单元上非零，所以Jacobi矩阵是带状矩阵。这些性质保证了非线性方程组可以用拟牛顿方法有效求解。

2 收敛性分析

本节采用矩问题的收敛理论[17-18]分析了计算二维映射不变测度的最大熵方法的收敛性，并给出误差分析。

设X是凸拓扑向量空间，令W:L1(X)→[-∞,∞)是X上具有紧水平集的泛函，{Dn}是L1(X)上的闭集序列，且对于所有的n都有Dn+1⊂Dn。考虑最大值问题

(22)

和极限问题

(23)

设对于每个n，fn是式(22)的解。

引理1[18]如果f*是式(23)的唯一解且满足W(f*)>-∞。那么在拓扑X下，函数序列fn收敛到f*，序列W(fn)收敛到W(f*)。

熵H(f)=-∬Xf(x,y)lnf(x,y)dxdy满足一般理论的所有条件。如果将X剖分成2*2n(n=1,2,…)，如图1中的嵌套直角三角形即Dn+1⊂Dn，式(10)的可行集对于包含关系是单调递减的。根据引理1有下列性质：

性质1 若H(f*)>-∞，那么对于Dn的最大熵的解fn有

a)当n→∞时，fn弱收敛到f*。

b)当n→∞时，H(fn)→H(f*)。

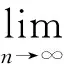
此方法的收敛率依赖于函数lnf*到由所有φi张成的子空间的最小距离[19]

(24)

由收敛理论和二维空间中连续函数的分片线性插值理论，可以得到下面的误差估计。

定理3 假设X上的f*(x)≥c，c是一个正数，f*在[a,b]上是连续可微的。则

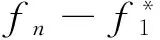
(25)

其中，δ是三角形的最大直径。

3 数值实验结果

本节把基于三角单元的分片线性最大熵方法应用到具体例子。数值结果表明收敛阶与理论估计一致。

例1 考虑二维映射

S(x,y)=(S1(x),S2(y))，

其中：

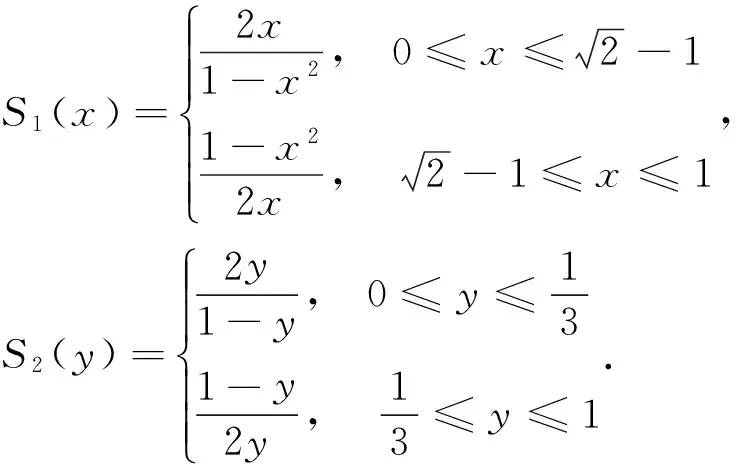
表1 S(x,y)和T(x,y)不变测度fn的L1-误差

对于大多数映射，其不变测度是未知的，则假设映射是遍历的，由Birkhoff的逐点遍历定理[20]有：

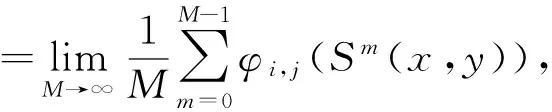
选择一个足够大的正整数M，可得矩的近似值为：

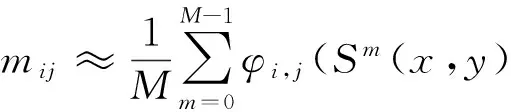
例2 考虑二维映射

T(x,y)=(T1(x),T2(y))，

其中:

T2(y)=4y(1-y).

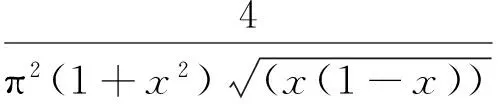
4 结 论

本文将基于有限元中分片线性三角元基函数的最大熵方法进行推广,用于计算二维映射的不变测度。选用三角单元上的分片线性基函数作为矩函数，其满足单位分割性质和支集性质，使得非线性方程组的Jacobi矩阵是正定的带状矩阵，简化了方程组的求解，提高了解的精度，保证了非线性方程组解的稳定性。数值实验结果表明，用基于分片线性基函数的最大熵方法计算二维映射的不变测度是有效并且收敛的。按照同样的思路，可把此方法推广到高维问题，但计算量会随之增大。

[1]FRENKELD,SMITB.Understandingmolecularsimulation:fromalgorithmstoapplications[J] . 2nded.PhysicsToday,1996,50(7):66.

[2]GORAP,BOYARSKYA,PROPPEH.Onthenumberofinvariantmeasuresforhigher-dimensionalchaotictransformations[J].JournalofStatisticalPhysics,1991,62(3):709-728.

[3]UlamSM.Bookreviews:Acollectionofmathematicalproblems[J].Science,1960,132(3428):665-666.

[4]DINGJ,ZHOUAH.ConstructiveapproximationsofMarkovoperators[J].JournalofStatisticalPhysics,2001,105(5):863-878.

[5]BOYARSKYA,GORAP.LawsofChaos[M].Boston:BirkhäuserBoston,1997:45-50.

[6]JAYNESET.Informationtheoryandstatisticalmechanics[J].PhysicalReview,1957,106(4):620-630.

[7]PEYMANESLAMI,MICALMISIUREWICZ.Singularlimitsofabsolutelycontinuousinvariantmeasuresforfamiliesoftransitivemaps[J].JournalofDifferenceEquations&Applications,2012,18(4):739-750.

[8]DINGJ,NOAHHRHEE.Birkhoff'sergodictheoremandthepiecewise-constantmaximumentropymethodforFrobenius-Perronoperators[J].InternationalJournalofComputerMathematics,2012,89(8):1-9.

[9]BARNHARTPR,GILLAMEH.Theimpactofsamplingmethodonmaximumentropyspeciesdistributionmodelingforbats[J].ActaChiropterologica,2015,16(8):241-248.

[10]JINCM,DINGJ.SolvingFredholmintegralequationsviaapiecewiselinearmaximumentropymethod[J].JournalofComputationalandAppliedMathematics,2016,304:130-137.

[11]MEADLR.ApproximatesolutionofFredholmintegralequationsbythemaximumentropymethod[J].JournalofMathematicalPhysics,1986,27(12):2903-2907.

[12]GALLISMA,HARVEYJK.Maximumentropyanalysisofchemicalreactionenergydependence[J].JournalofThermophysics&HeatTransfer,2015,10(2):217-223.

[13]SIDDIQIMH,ALAMMGR,HONGCS,etal.AnovelmaximumentropyMarkovmodelforhumanfacialexpressionrecognition[J].PlosOne,2016,11(9):3-8.

[14]GULLSF,SKILLINGJ.Maximumentropymethodinimageprocessing[J].CommunicationsRadar&SignalProcessingIeeProceedingsF,1984,131(6):646-659.

[15]FERNANDEZJE,SCOTV,GIULIOED.SpectrumunfoldinginX-rayspectrometryusingthemaximumentropymethod[J].RadiationPhysics&Chemistry,2014,95(4):154-157.

[16] 文兰.动力系统简介(迎接ICM2002特约文章)[J].数学进展,2002,31(4):293-294.

[17]TEBOULLEM,VAJDAI.Convergenceofbestφ-entropyestimates[J].IEEETransactionsonInformationTheory,1993,39(1):297-301.

[18]LEWISAS.Theconvergenceofentropy-basedapproximationsformomentproblems[J].Optimization,2010,28(3):383-395.

[19]MACKEY,MICHAELC.Chaos,Fractals,andNoise[M].Berlin:Springer-Verlag,1994:97-100.

[20]BISWASP,SHIMOYAMAH,MEADLR.Lyapunovexponentsandthenaturalinvariantdensitydeterminationofchaoticmaps:aniterativemaximumentropyansatz[J].JournalofPhysicsAMathematical&Theoretical,2009,43(12):835-842.

(责任编辑： 康 锋)

Application of Maximum Entropy Method in Calculating Two-Dimensional Invariant Measure

ZHANGRu,XUChunwei,JINCongming

(School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018, China)

The piecewise linear basis function on the triangle unit is used as the moment function in maximum entropy method to calculate invariant measure of two-dimensional mapping. Since the piecewise linear basis function on the finite element unit has local support set and unit partition property, Jacobi matrix of nonlinear equations obtained from the maximum entropy method is positive band matrix, which guarantees the uniqueness and stability of the solution. In theory, this paper gives convergence degree of this method, and numerical experiment results are consistent with the theory.

finite element unit; invariant measure; piecewise linear basis function; maximum entropy

10.3969/j.issn.1673-3851.2017.07.017

2016-11-14 网络出版日期： 2017-03-28

国家自然科学基金项目(11571314)；浙江省自然科学基金项目(LY13A010014)；浙江理工大学521人才培养计划项目

张茹(1990-)，女，河北石家庄人，硕士研究生，主要从事动力系统和分子模拟等方面的研究。

靳聪明，E-mail：jincm@lsec.cc.ac.cn

O242.21

A

1673- 3851 (2017) 04- 0569- 06