碎纸片的拼接复原
2017-08-16郭蓉段玉洁通讯作者济南大学数学科学学院
郭蓉 段玉洁(通讯作者) 济南大学数学科学学院
碎纸片的拼接复原
郭蓉 段玉洁(通讯作者) 济南大学数学科学学院
随着人类社会信息化程度的不断提高,破碎文件复原技术在航空航天、医学图像分析、计算机视觉、视频监控等领域的应用前景十分广阔,由于人力工作的限制,运用相关拼接复原模型,深入研究该项技术有着很重要的意义。对一页纵切印刷文件碎纸片,采用基于边界相关的拼接算法,建立拼接复原模型。利用MATLAB软件求灰度矩阵并进一步求相关系数矩阵的方法,根据相关系数的高低得出图片的连接顺序。
灰度矩阵 相关系数矩阵 边界拼接
1 问题假设
①因为一张纸是平均分割,所以假设每个纸片的形状完全相同。
②因为图像间的位置误差是相邻图像间的拼接误差的主要因素,所以不妨假设接缝处的误差只源于相邻图像间的位置误差。
③假设应用软件的图像数据读取不存在误差。
2 模型的建立与求解
2.1 数据预处理
将图像在MATLAB中得到的灰度矩阵,通过数字化预处理应用double命令转化为数值矩阵。
2.2 对一页纵切印刷文件碎纸片情形模型的建立与求解
2.2.1 模型的建立
采用基于边界相关的拼接算法建立拼接复原模型。相关系数:

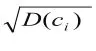
2.2.2 模型的求解与分析
模型求解:利用MATLAB编程将碎纸片复原。
步骤一:将图片依次编号,用MATLAB读取n个图片,得到n个灰度矩阵,再转化为数值矩阵;
步骤二:将每个数值矩阵的第一列和最后一列提取出来,分别标号为 c2i−1,c2i(i=1…n),n个数值矩阵的第一列和最后一列一共组成一个矩阵F,再利用MATLAB中的求相关系数矩阵的命令 H= corrcoef(F),得到一个 2n× 2n的相关矩阵:

其中 ci,j表示 ci与 cj的相关系数 ρi,j,且R为对称矩阵。

属于同一行的两个结果即是相互拼接的两个边的序号,且是偶数边右接奇数边。
步骤四(干预时间节点):
干预方式:得到矩阵J我们只需找到原图片的最左边那张图(暂且编为图片一)的左边的序号 w1(可采用从矩阵J的元素中寻找未出现的标号即为此编号),然后加一得到此图片的右边的编号 w1+1,然后去矩阵J中寻找与图片一的右边的标号 w1+1在同一行的编号w2,此编号即为图片一的右接图片(暂且编为图片二)的左边的那条边的编号w2。然后加一得到图片二的右边那条边的编号 w2+1,依次循环下去。即得到一连串的序号一奇一偶,我们将偶数取出除以二即得到图片1-19的排列顺序。
步骤五:将碎片的数值矩阵按顺序连接,利用MATLAB命令得到复原图。
3 模型改进与评价
3.1 模型改进
我们可以对图像进行预处理。有以下几种预处理方法。
3.1.1 图像校正
图象校正的基本思路:找到图像失真原因,建立相应的数学模型,从被污染或畸变的图象数据中提取所需要的特征信息,使失真图像沿其逆过程恢复本来面貌。从失真图象中计算得到真实图象的估值,根据预先规定的误差准则,最大程度地恢复真实图像。
3.1.2 图像去噪
图像在成像、传输、转换或储存的过程中会受到各种随机干扰信号的影响,一般来说,噪声就是这种不可预测的随机信号。大多时候我们选择降噪滤波器对图像数据进行处理,其中最具代表性的滤波方法有均值滤波、中值滤波、自适应维纳滤波、形态学噪声滤除器、小波去噪等方法。
3.1.3 归一化
在给定变换下,图像的某些特征具有不变的性质。在一般情况下,影响变换对图像一些性质的因素,可通过归一化处理得到减弱或消除,从而可以被选作测量图像的依据。灰度归一化、几何归一化和变换归一化是获取图像不变性质的三种归一化方法。
第一作者:郭蓉,1996-,山东菏泽人,女,汉族,济南大学数学科学学院本科在读。通讯作者:段玉洁,1996-,山东菏泽人,女,汉族,济南大学数学科学学院本科在读。
