与数学结缘的皇帝

林革

众所周知，数学是科学和哲学的基础，是探索自然和理解世界的钥匙。在人类发展史中一直占据着极其重要的地位，受到古今中外统治者的高度重视似乎不足为奇，但能够像数学家一样痴迷其中、潜心探索，并取得不俗成就的君王并不多见。下面这两位分别来自东西方的皇帝，应该能够印证法国数学史家M.查斯莱的名言：历史表明，那些醉心数学，鼓励这一切精密科学的共同源泉发展的君王们，也正是那些威加四海、名扬千古的统治者们。

康熙 有数学著述的千古一帝

康熙（1654～1722）名愛新觉罗·玄烨，满清入关后的第二位皇帝，其文治武功在中国历代帝王中首屈一指，堪称秦始皇以来最伟大的君主之一。他8岁继位，14岁亲政，在位61年，是中国历史上有文字记载以来在位时间最长的一位君主。

康熙不仅文武兼备，而且好学勤政，他妥善处理民族之间的关系，开创了康乾盛世，促进了清朝初年社会经济的发展，奠定了中国多民族统一国家的疆域。更令人惊讶的是，康熙还被称为“最博学的皇帝”。他博览群书，学识渊博，不仅谙熟儒家典籍；而且通晓音律、自然、天文、地理，其对抽象深奥的数学情有独钟，表现出过人的天赋造诣，并取得了相当成就，为中国古代数学发展做出了极大贡献。这在中国古代封建皇帝中绝无仅有。

史料记载，康熙皇帝在位时，经常请懂数学的外国人给他讲西洋数学。当时，宫廷内聚集着许多数学家，形成了良好的学习氛围；好学勤思的康熙皇帝在其中显露出对知识的渴求和思考。下面的这则史实就能说明问题：

康熙皇帝曾拜比利时传教士南怀仁为师，学习数学。可以想象，面对一个汉语和满语水平极其有限的外国老师和严谨抽象的数学知识，康熙即便天资聪慧，在学习中也会面对重重困难。教者，表达描述上力不从心；学者，弄清理解更是难上加难。上好这样的数学课真的是一点也不轻松，康熙常常被搞得晕头转向。

怎样才能让老师讲的东西易于为己接受呢？经过一番思索，康熙向老师建议，将未知数简洁地翻译为“元”，最高次数翻译为“次”（限整式方程），把方程左右两边相等的未知数的值翻译为“根”或“解”……皇帝的建议当然应该重视起来，不过，当南怀仁开始真正使用这些带有独创性的数学名词时，他惊异地发现，用这些新术语表达是多么方便，与自己原先使用的烦琐词语有着天壤之别，这简直是了不起的发明。对皇帝刮目相看的他记下了上面提到的这几个便于理解和记忆的数学术语，并流传沿用至今。如今，我们学习解方程时，总会碰到“元”“次”“根（解）”等术语，这些术语就是康熙皇帝所创。

康熙皇帝在位时期，经常与数学家探讨数学问题，其中，大学士陈厚耀就是与其频繁交往的一位。康熙皇帝在1705年召见了清朝第一历算家梅文鼎，亲自问数学；后来，还召梅文鼎的孙子梅瑴成入宫，教导他数学。到了晚年，康熙建议编纂一部融合中国和西欧数理科学的书。于是，由陈厚耀等人牵头，何国宗、梅瑴成等数学家编纂了一部清朝最著名的数学百科全书——《数理精蕴》。此书对日本的数学产生极大影响。这本书有“钦定”两字，表明此书是由康熙皇帝亲自确定编纂的。另外，在北京图书馆藏有康熙时期所著的《三角形论》一书，书上标有“御纂”二字，表示康熙当时亲自参与了这本书的编辑。

2003年，由清康熙年间一流数学家陈厚耀修撰的专著《陈厚耀算书》在西安被发现，这是迄今发现的第二部康熙数学著述。此消息引起了广大历史、数学爱好者的浓厚兴趣。这本数学专著全书分为六册，由康熙口授、陈厚耀笔录的“以积求勾股”属于第六册中“勾股图解”的一篇。在“积求勾股法”中，康熙论述了5种求解直角三角形问题的解法，并以其中“以积求勾股”作为标题，同时加以“钦授”字样，表明了这个方法是康熙的发明创造。康熙是中国历史上有据可考的对数学问题提出解法的唯一一位帝王。

康熙皇帝为何能在数学上取得如此成就，只要我们到故宫博物院里去看一看就能得到答案。为了便于数学教学，康熙皇帝特制了一个楠木炕桌。桌面上刻着各种直线、斜线、横线，并标志着许多数字以及精确度为千分之一的分厘尺。一块上刻着“开平方”和“求圆半径”字样，另一块刻有“开立方”和“求球半径，又测米堆”字样。这个炕桌至今仍保存在故宫博物院，足见康熙皇帝对数学的酷爱和重视。

由此就不难理解，在中国历史上，皇帝主动学习数学的就很少，有著述者更是凤毛麟角。康熙对数学的喜爱在中外历史上都是罕见的，也是中国历代帝王中唯一留有数学著作的人。作为帝王，康熙在数学史上留下了令人赞叹的一页。

拿破仑 靠数学打仗的战争之神

似乎是冥冥之中注定，又似乎说明无独有偶，与古老东方遥遥相对的西方，在数十年后也出现了一位与数学结缘的君主，他就是赫赫有名的法兰西第一帝国皇帝拿破仑。

拿破仑·波拿巴（1769～1821），19世纪著名军事家、政治家。或许许多人并不知道，这位叱咤风云的人物同时也是一位数学家。事实上，拿破仑风起云涌、波澜壮阔的传奇生涯与数学有着不解之缘，与数学相关的背景挥之不去。

拿破仑出生于科西嘉岛的平民家庭，少年时期就对数学产生浓厚的兴趣。拿破仑10岁时进入布里埃纳军校学习，督察官一年一度例行检查每个学生的学科成绩，对拿破仑的评价报告中写着：“他在数学方面成绩非凡。”1784年，著名数学家拉普拉斯发现了拿破仑的数学才华，这成为他报考法国皇家陆军学院的一个重要原因。在炮兵专业学习期间，勤奋努力的拿破仑掌握了大量数学知识，并于次年以优异成绩提前毕业。后来，他在服役期间撰写的一篇弹道学论文，其中严密的数学推导和计算，就证实了他过硬的数学功底。

拿破仑在数学方面的过人素养和非凡造诣，在他担任炮兵军官时大放异彩。

1805年，拿破仑率军与普鲁士、俄国联军在莱茵河南北两岸对阵。两军都想向对方阵地开炮；但是，不知宽度的莱茵河成了双方的阻碍，没有精确射程的炮击成了浪费弹药的竞赛。在这種情况下，谁能率先测量出河的宽度，谁就能占得先机。

拿破仑为解决这个难题，每天远眺莱茵河，在岸边来回踱步。有一次，他偶然发现，对岸的边线（北岸线）恰巧擦着自己戴的军帽的边沿，于是，计上心来。他在这个地点做了一个记号，然后沿着莱茵河的垂直方向一步一步往后退，一直退到莱茵河南岸线也擦着自己军帽沿的地方，停下来又做了个记号。拿破仑让部下丈量出这两个记号之间的距离，并告诉部下：“这就是莱茵河的宽度。”

当天傍晚，经过重新校准的法军大炮一齐向对岸敌军阵地射击。炮弹就像长了眼睛般，纷纷飞入敌营。敌军顿时大乱，全线溃败，而法军凭借拿破仑的数学智慧大获全胜。

据说，拿破仑对几何学有着特别的兴趣。在他统治法国之前，曾与法国大数学家拉格朗日及拉普拉斯一起讨论过几何问题。拿破仑的过人才智和真知灼见令数学家们叹服，以至于他们一起请求：“将军，你来给大家上一次几何课吧！”这样的说法似乎有吹捧夸张之嫌，不过，拿破仑对几何的情有独钟是有据可查的。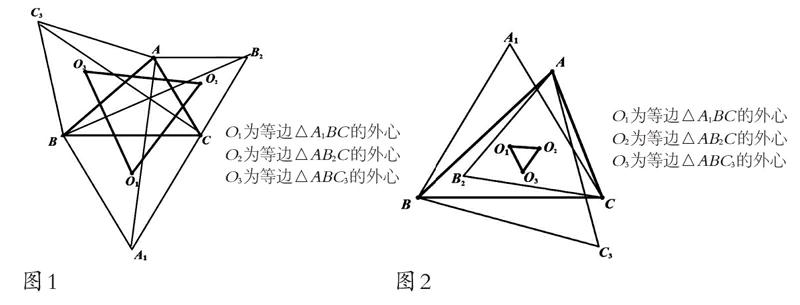

史料记载，拿破仑攻占意大利之后，把意大利图书馆中有价值的文献，包括欧几里得的名著《几何原本》都运回了巴黎。当他阅读了意大利数学家马克罗尼的几何著作后，就给法国数学家提出过“如何仅用圆规将已知圆心的圆周四等分”的问题，后被法国数学家曼彻罗尼所解决，其巧妙思路至今仍为广大数学爱好者津津乐道。

除此之外，几何史上的一些名题也和拿破仑有着关联。“拿破仑三角形”就是其中最著名的范例：如果从一个任意三角形的三边上向外或向内分别做3个正三角形，那么连结这3个三角形的中心，得到仍是一个正三角形，后人称之为“拿破仑三角形”（如下图）；在图1中，AA1、BB1、CC1三线共点，且AA1=BB1=CC1，这个命题被称为“拿破仑定理”。后来，人们又发现了“拿破仑三角形”其他一些妙不可言的性质，它们深刻地揭示了几何量之间的内在关系，同时也充分体现了几何图形的和谐美和对称美。

拿破仑不仅精通数学，更难能可贵的是，他还非常珍惜数学人才和重视普及数学知识。在拿破仑的眼里，一个将军远没有一个数学家重要。因此，当1814年俄、奥、普联军兵临巴黎城下时，一些数学学院的学生要求参军应战，拿破仑坚决地拒绝了他们的要求，理由是：“我不能为了一场战争的胜利而杀死生金蛋的母鸡。”拿破仑曾坦言，他如果不是将军的话，会选择去做一名数学教授。他还说：“一个国家只有数学蓬勃发展，才能表现它的国力强大。”在统治法国期间，拿破仑要求学生必须学习充分的数学课程。这一传统对现代法国学校的课程改革产生了重大影响。

【责任编辑】赵 菲