基于去伪控制的加热炉控制问题研究
2017-08-11贾志闻
黄 伟, 贾志闻
杭州娃哈哈集团有限公司 杭州 310018
基于去伪控制的加热炉控制问题研究
黄 伟, 贾志闻
杭州娃哈哈集团有限公司 杭州 310018
研究了基于去伪控制的加热炉控制问题,设计了对应的去伪控制器,并应用Matlab软件进行了仿真分析。结果表明,所设计的去伪控制器能较好地控制加热炉炉温,无稳态误差,且切换速度快,具有良好的暂态性能。
加热炉; 去伪控制; 温度
随着科学技术的发展,生产过程日趋复杂。基于精确数学模型的传统控制方法对复杂生产过程进行控制变得越来越困难[1]。去伪控制是一种利用在线数据直接辨识控制器的数据驱动控制方法[2],基本思想是构造一个满足性能指标的可行控制器参数集合,基于测量到的新数据迭代判断是否满足此性能指标,再根据去伪算法选择适合的非伪控制器,加入控制链[3]。去伪控制基于在线数据选择控制器,实现起来比较方便,因此具有较高的实时性与可实现性[4-5]。工业加热炉作为生产过程中极为重要的常见设备,其建模与高精度控制较困难[6-11]。普通比例积分微分(PID)控制器的控制参数需通过经验确定,不利于最优控制,所以研究基于去伪控制的加热炉控制问题具有很强的现实意义。
1 去伪控制基本理论
去伪控制理论中,当被控制对象(P)完全未知或部分已知时,希望能够充分利用测量到的数据(u,y)去选择合适的控制器(k),并且能够保证闭环系统稳定。
若一个控制器(k)通过测量到的信息(Pdata)证实是无效控制器,即此控制器在控制器回路中不能满足性能指标的要求,则称此控制器为伪控制器;否则为非伪控制器。
如果一个控制器(k)通过测量到的信息(Pdata)证明是非伪的,那么当且仅当每一组(r0,y0,u0)∈Pdata∩K都存在至少一组测量到的数据(u1,y1),使(r0,y1,u1)∈Pdata∩K∩Tspec,其中Tspec为性能指标集合,K为控制器集合[3]。
证明如下: 参考信号r0∈R能够产生对应控制器(k)数据的条件是控制器(k)应在回路中,即对应(r0,y0,u0)∈Pdata∩K;如果控制器(k)为非伪控制器,那么条件为当且仅当控制器(k)在回路中,r0产生的一组数据(u1,y1)满足性能指标,即(r0,y1,u1)∈Tspec;所以当且仅当控制器(k)为非伪控制器时,(r0,y1,u1)∈Pdata∩K。
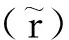
2 在加热炉控制系统中的应用
令性能指标J(t)为积分不等式的形式,即:
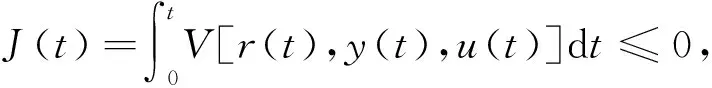
(1)
式中:V为关于r、y、u的函数,根据设计需求选择。
(2)
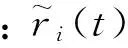
为了仿真需求,将性能指标离散化。令任意时刻τ=nΔt(n=1,2,3…,Δt为离散时间),可将式(2)离散化为:
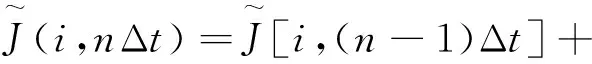
y[(n-1)Δt],u[(n-1)Δt]}}
(3)
笔者所选满足性能指标的集合Tspec取为‖ω1×(r-y)‖2+‖ω2×u‖2≤‖r‖2,于是可得:
V[r(t),y(t),u(t)]=|ω1×[r(t)-y(t)]|2+
|ω2×u(t)|2-|r(t)|2
(4)
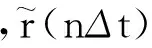
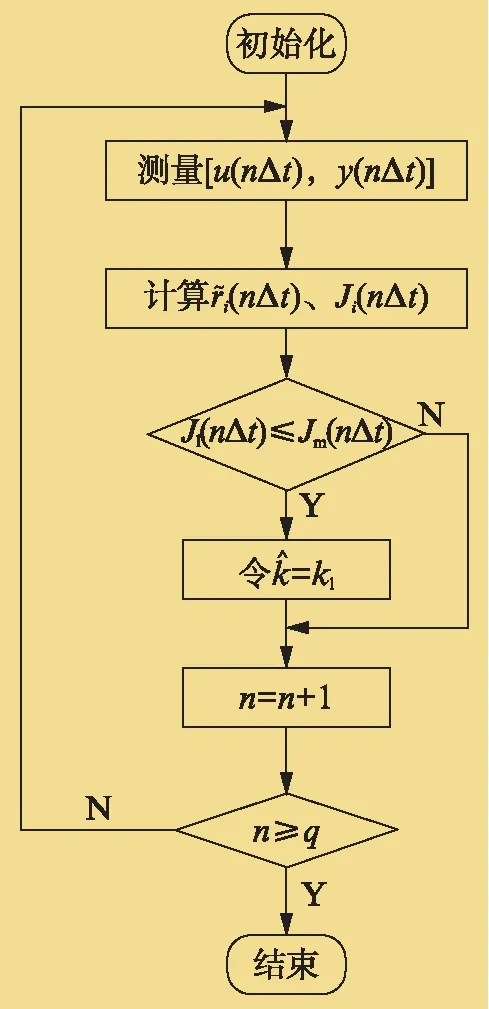
图1 基于去伪控制的PID参数整定方法流程
笔者使用Matlab及Simulink进行仿真,仿真时所用的数据如下。
加热炉模型的传递函数[7,10]为:
(5)
采样时间Δt为0.05s,仿真时间为20s。
候选控制器为120组PID控制器,即比例KP={1,5,10,25,50,100},积分KI={1,5,10,30,40},微分KD={1,4,10,15},输入信号为r脉冲信号,幅值为1。
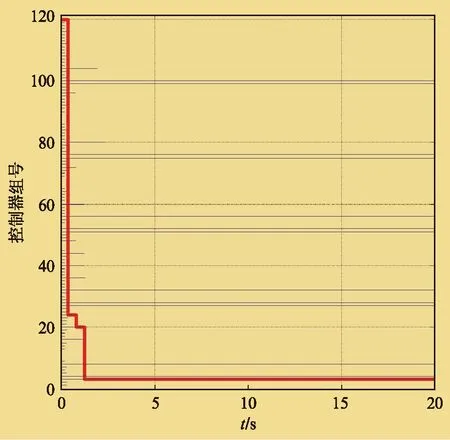
图2 控制器切换曲线
由图2可知,随着时间的推移,不断有伪控制器被丢弃。系统总共进行了3次切换,且切换时间均短于2s,这样能够迅速将不稳定的伪控制器切换出回路,从而保证整个系统的动态性能良好。
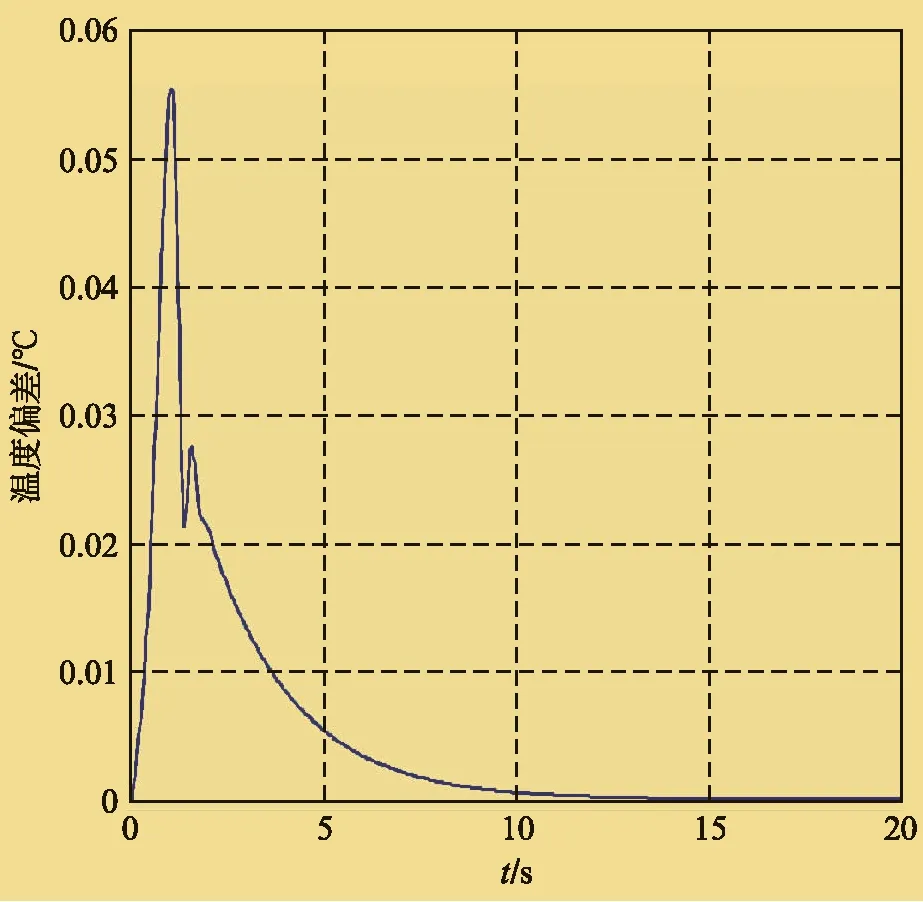
图3 温度偏差变化曲线
图3中纵坐标表示受到外界干扰(如风压、燃气压力波动等,仿真中以脉冲函数代替)后,炉温与设定温度的偏差,炉原本处于保温阶段,温度为900℃。由图3可知,所设计的去伪控制器对被控对象的控制输出较平滑,系统没有稳态误差,超调量小,很好地实现了加热炉温度控制,稳定时间为10s。
3 总结
笔者研究了基于去伪控制的加热炉控制问题,设计了相应的去伪控制器,并进行了仿真,确认所设计的去伪控制器能够很好地控制加热炉系统的温度偏差,无稳态误差,且切换速度较快,可以在2s内完成切换。切换仅3次,避免了频繁切换,使系统具有良好的暂态性能。当然,去伪控制有一个基本的条件,即控制器集合中至少有一个非伪控制器。只有满足了这个基本条件,才能通过去伪控制算法选择控制器。利用去伪控制算法可以迅速剔除伪控制器,将非伪控制器切换至系统回路中,保证系统的暂态性能。
[1] 侯忠生,许建新.数据驱动控制理论及方法的回顾和展望[J].自动化学报,2009,35(6): 650-667.
[2] FRANCIS B A, TANNENBAUM A R. Feedback Control, Nonlinear Systems and Complexity[M]. London: Springer, 1995: 196-214.
[3] SAFONOV M G, TSAO T C. The Unfalsified Control Concept and Learning [J]. IEEE Transactions on Automatic Control, 1997,42(6): 843-847.
[4] TSAO T C, SAFONOV M G. Unfalsified Direct Adaptive Control of a Two-link Robot Arm [C]. Control Applications, 1999. Proceedings of the 1999 IEEE International Conference on, Kohala Coast, 1999.
[5] JUN M, SAFONOV M G. Automatic PID Tuning: an Application of Unfalsified Control [C]. Computer Aided Control System Design, 1999. Proceedings of the 1999 IEEE International Symposium on, Kohala Coast, 1999.
[6] 诸键,苏宏业,于军,等.工业电加热炉时滞状态空间模型的辨识[J].控制与决策,1994,9(1): 74-77.
[7] 杨晓东,杨树发.连续加热炉温度的数学模型[J].工业技术经济,2002(5): 101-102.
[8] 任涛,高振华,祖国旗,等.去伪控制方法的研究与应用[J].东北大学学报(自然科学版),2009,30(12): 1678-1681.
[9] 高林,顾幸生,刘喜梅.去伪控制及其应用研究[J].化工自动化及仪表,2010,37(6): 13-15.
[10] 边军,张福波,刘相华,等.红外线加热炉温度PID控制及优化[J].东北大学学报,2004,25(8): 771-773.
[11] 王全刚,程良伦,李锦棠,等.基于模糊PID算法的挤出机机筒温度控制系统设计[J].机械制造,2015,53(2): 23-26.
(编辑: 平 平)
The control issue of the heater was studied based on the de-fake control. The corresponding de-fake controller was designed and simulated for analyses by Matlab software. The results show that the design of the de-fake controller can provide a better control of the heater temperature without any steady-state error while its switching speed is quick and transient performance is satisfied.
Heater; De-fake Control; Temperature
2016年12月
黄伟(1983— ),男,硕士,工程师,主要从事自动化控制研究工作, E-mail: huangtianxia608@163.com
TM571
A
1674-540X(2017)02-028-03
