财经类院校《概率论》课程中的案例教学法

赵洁

（内蒙古财经大学统计与数学学院，呼和浩特 010070）

财经类院校《概率论》课程中的案例教学法

赵洁

（内蒙古财经大学统计与数学学院，呼和浩特 010070）

案例教学法在教学实践环节中把生活中的实际问题作为案例组织教学材料,通过分析案例,让学生参与讨论并提出解决问题的基本方法和途径,这样能充分调动学生的主观能动性，达到教学目的。针对案例教学法在课程中的应用,结合教学实践与理论思考,给出常用的几个具体案例,把抽象的概率知识与生动有趣的案例结合起来,培养学生的学习兴趣以及分析解决问题的能力。

概率论；案例教学法

0 引言

近年来,随着运筹学、博弈论等相关理论在社会中的广泛应用,统计学、多元统计分析理论在各专业领域的普及,《概率论》[1,2]作为随机数学中的重要基础课程,是一门研究随机现象客观规律的学科.由于随机现象的普遍性决定了该学科应用的广泛性,在各个行业部门,包括工业、农业、医学、科技、国防、金融、经济、管理等领域得到广泛应用。因此,它的学习方法不同于学生之前所学习的高等数学、线性代数等其他数学课程。通过这门课程的学习,学生要学会用随机性思维去分析和解决问题。但是,大多数学生在学习这门课程时常常感觉到概念抽象,方法难以掌握.著名科学家爱因斯坦说过“兴趣是最好的老师”,这就是在强调兴趣的重要性,兴趣能够提供最直接的学习动力,也是学习新知识的开端是学习动机中最现实、最活跃和最实际的因素,激发学习兴趣也是教学中激发学生学习的一种策略。《概率论》是一门实用性很强的学科,有很好的直观背景,如果能够充分激发学生的学习兴趣,让学生积极主动地去学习这门课程,将会达到事半功倍的效果。教学案例是真实而又典型且含有问题的事件。简单地说，一个教学案例就是一个包含有疑难问题的实际情境的描述，是一个教学实践过程中的故事,描述的是教学过程中“意料之外,情理之中的事”。通过案例教学法,可以让学生生动形象地了解概念所表达的含义,更好地理解定理的思路、例子的实际意义,在理解后能够让学生有豁然开朗的感觉.所以在讲解概念和公式时,需要举出贴切的例子,做到深入浅出、恰到好处。

1 条件概率与乘法公式——抽签公平吗？

例1：假设5名同学想去看演唱会,但只有一张门票,大家商量用抽签的方法决定由哪名同学去看演唱会,5名同学依次抽取,考虑：抽取到演唱会门票的机会与抽签顺序有关吗？

解：设Ai(i =1,2,3,4,5)表示第i名同学抽到演唱会门票。

则：第一名抽签的同学抽中演唱会门票的概率为P(A1)=。

依此类推,得到每名同学抽中演唱会门票的概率P(Ai)=。

因此,抽签不分先后,抽签的先后顺序并不影响抽取的机会,我们在抽签时,不必争先恐后,也不必畏缩不前。

2 事件的独立性——根筷子容易折,一捆筷子抱成团

例2[3]：假设一根筷子能够被折断的概率为p,求n只相同的筷子同时被折断的概率。

解:每只筷子能否被折断是相互独立的,则n只相同的筷子同时被折断的概率为：

p×p×…×p=pn

特别地,当 p=0.75时,n只相同的筷子同时被折断的概率见表1：

表1

通过上表可以看出,折断一根筷子是轻而易举的,筷子数量越多时,一捆筷子被折断的概率越小,当n=25时,被折断的概率只有0.0008。

说明了合作是一种力量,无论在哪个领域,无论从事什么职业,要想顺利完成一项工作,都离不开与他人的合作,每个人的能力都是有限的,知识也是有局限的,只有通过合作的方式,才能顺利完成。

3 数字特征——正态分布的期望和方差

例3：某人去火车站乘火车,有两条路可以走,第一条路程较短,但交通拥挤,所需时间X～N(4 0,100)；第二条路程较长,但以外堵塞较少,所需时间Y～N(5 0,16)。

求:（1）若动身时离开车时间有60分钟,应该走哪条路？

（2）若动身时离开车时间有45分钟,应该走哪条路？

解:（1）若动身时离开车时间有60分钟,应该走哪条路？

若选择第一条路：

若选择第一条路：

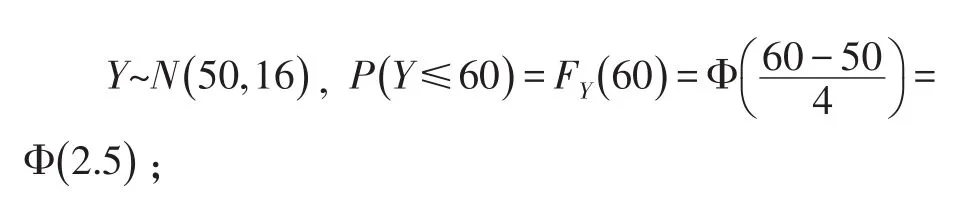
根据分布函数的性质：Φ(2 .5)>Φ(2),若动身时离开车时间有60分钟,应该选择第二条路。

（2）若动身时离开车时间有45分钟,应该走哪条路？

若选择第一条路：

因此,若动身时离开车时间有45分钟,应该选择第一条路。

这与生活中的经验是相一致的,若时间紧迫,则应该选择路程较短,但交通拥挤的第一条路；若时间宽裕,则应该选择路程较长但以外堵塞较少的第二条路。

从概率的意义来看,数学期望反映了取值的加权平均,方差反映的是一组数据与其平均值——数学期望的偏离程度.第一条路所需时间X～N( ) 40,100,即若选择第一条路,平均所用时间为40分钟,一般用时为(40-10,40+10)之间；第二条路Y～N(5 0,16),即若选择第二条路,平均所用时间为50分钟,一般用时为(50-4,50+4)之间.因此,若只有60分钟,则应该选择第二条路,若只有45分钟,则应该选择第一条路。

4 概率推理——“捡芹菜”与“娶媳妇”

在日常生活中经常会遇到许多不确定的信息,即有概率性质的信息,若据以推理,就是概率推理。例如：阴天不一定意味着下雨,肚子痛不一定是吃坏了肚子。

例4：在网上流传一个段子：今天走在路上,看地上有捆芹菜,捡还是不捡？仔细一想,有芹菜就要买肉,买了肉就要有厨房,厨房有了,那就必须要有个媳妇儿来做,有个媳妇儿就肯定有丈母娘,你要想娶她姑娘,她就必须开条件了,要房、要钱、要车,仔细想了想,赶紧把芹菜扔了,现在房价跌这么厉害,肯定是开发商故意扔的,这太吓人了。试用概率的思想分析合理性。

解:这道例题的分析并不合理。

因为有了芹菜,不一定要买肉；买了肉,不一定要有厨房；有了厨房,不一定要有媳妇儿；有了媳妇儿和丈母娘,丈母娘也不一定会开条件；开条件也不一定是要房、要钱、要车。

假设每件事发生与否是等可能的,即：

5 全概率公式与贝叶斯公式——狼来了

例6：伊索寓言“孩子与狼”讲的是一个小孩每天到山上放羊,山里有狼出没,第一天他在山上喊：“狼来了！狼来了！”山下的村民闻声便去打狼,可到了山上,发现狼没有来；第二天仍是如此；第三天,狼真的来了,可无论小孩怎么喊叫,也没有人来救他,因为前两次他说了谎话,人们不再相信他了。试用贝叶斯公式分析这个寓言中村民的心理活动。

解:先做一些假设。首先假设村民们不认识这个小孩,没有先入为主的印象,他说谎话（记为A1）和说真话（记为A2）的概率相同,即设：

另外,由于小孩说谎话时,并不知道狼会不会来,因此再假设：说谎话喊狼来了（记为B）时,狼来的概率为1/3,说真话喊狼来了时,狼来的概率为3/4,即设：

当村民第一次上山打狼,发现狼没有来（记为Bˉ）时,村民们对说谎话小孩的认识反映在条件概率P()上,根据上述假设,利用贝叶斯公式可以算得：

在此基础上,村民们第二次上山打狼,仍没有看见狼,这时村民们再一次调整对这个小孩的认识,即再一次计算条件概率P(),即：

这表明,村民们经过两次上当,对这个小孩说谎话的概率从0.5上升到0.8767,即村民们认为这个小孩说的十句话中有近九句话在说谎,这个小孩给村民们留下这种印象,在村民们听到第三次呼叫时怎么会再上山打狼呢？

6 结语

概率论作为研究随机现象的统计规律性的学科,与其他数学基础课明显不同,它的知识来源于生活的实际问题,在生活和社会实践中的应用比比皆是,并有其深刻的实际背景,在工科、管理学科等专业领域都有广泛的应用,比如生日问题、彩票的发行及购买问题、质量检测控制问题、交通事故问题、工厂库存问题、组合证券投资决策问题、保险公司赢利问题、报童问题等.因此在课堂教学中适当引入相关的案例,会使得上课更加生动有趣,不同于常规数学课程的举例一定会引起学生的好奇心,从而激发学生对概率论课程学习的极大兴趣。

参考文献：

[1]李贤平.概率论基础（第三版）[M].北京：高等教育出版社,2010.

[2]茆诗松，周纪芗.概率论与数理统计（第三版）[M].北京:中国统计出版社，2007.

[3]王琼.谚语中的概率论[J].西藏大学学报（自然科学版）[J],2009，24（2）:106-108.

Case Teaching Method for Probability Theory Course Teaching in Finance and Economics Colleges

ZHAO Jie

（School of Statistics and Mathematical,Inner Mongolia University of Finance and Economics,Hohhot 010070)

Case teaching method in the teaching practice uses the practical problems of life as the cases of teaching materials,makes students partici⁃pate in the discussion,and puts forward the basic methods and ways to solve the problem by analyzing the cases,then fully mobilize the ini⁃tiative of the students and achieve teaching objectives.For the application of case teaching method in the course of probability theory,com⁃bines with teaching practice and theoretical thinking,gives several particular cases,and combines abstract probabilistic knowledge with a lively and interesting case to develop students'interest in learning and ability to analyze and solve problems.

赵洁（1984-），女，内蒙古包头人，硕士研究生，在读博士，讲师，研究方向为概率论及经济统计

2017-03-23

2017-05-25

1007-1423（2017）16-0043-04

10.3969/j.issn.1007-1423.2017.16.011

Probability Theory;Case Teaching Method