基于粒子群算法的电力系统无功优化*
2017-08-09庹先国彭桂力
陆 景,庹先国,彭桂力
(1. 四川理工学院 自动化与信息工程学院,四川 自贡 643000; 2. 西南科技大学 信息工程学院,四川 绵阳 621010;3. 天津城建大学 控制与机械工程学院,天津 300384)
基于粒子群算法的电力系统无功优化*
陆 景1,2,庹先国1,2,彭桂力2,3
(1. 四川理工学院 自动化与信息工程学院,四川 自贡 643000; 2. 西南科技大学 信息工程学院,四川 绵阳 621010;3. 天津城建大学 控制与机械工程学院,天津 300384)
针对电网电力传输的无功功率优化,可以改善全网的无功分布。合理的无功分布既可以保证网络电压质量又可以有效降低网络有功损耗,直接影响着电力系统的安全与稳定,并与经济效益直接挂钩。文中采用基于惯性权重的粒子群算法研究电力系统无功优化,建立以最小网损为目标函数、通过罚函数的形式引入负荷节点电压和发电机无功功率越限处理的数学模型;并建立电力系统无功优化仿真程序,以IEEE-30节点系统进行仿真计算。结果表明,该算法能获得全局最优解,优化后网损率下降16.11%。
无功优化;粒子群算法;系统网损;IEEE-30系统仿真
0 引言
随着生产自动化、智能化的发展,市场对电力的负荷需求增加,并对供电的可靠性及质量等提出更高的需求,而峰差越来越大、电压过高或过低等问题愈加频繁,导致系统调压愈加困难[1]。无功优化则是在系统有功潮流分布确定的前提下优化系统的控制变量,使系统性能指标达到最优[2],因此研究电力系统无功优化具有重要意义。
现有电力系统无功优化研究工作可归类为:(1)数字优化算法,如线性及非线性规划法、内点法、牛顿法等,通过求解连续、单峰、可微的非线性函数,解决系统优化问题,然而此类方法在处理离散函数时具有困难,不能实现全局优化;(2)基于人工智能优化算法,如粒子群算法和遗传算法等,对离散约束条件的多目标优化问题具有较强适应性[3]。
本文针对采用基于惯性权重参数的粒子群优化算法,以IEEE-30 标准节点系统为研究对象,对电力系统无功优化问题展开研究,建立粒子群优化IEEE-30的潮流计算仿真模型,研究算法对各参数优化结果。
1 电力系统无功优化
粒子群优化算法是一种基于群体智能的演化计算技术,被成功应用到函数优化、神经网络设计、机器人技术等领域。同时算法在电力系统领域的研究也受到重视,在配电网扩展规划、负荷经济分配、最优潮流计算与无功优化控制等方面有相应研究成果,且在电力市场仿真等领域具有应用潜力[4]。
1.1 无功优化目标函数
无功优化目标函数各有差异,主要有以系统有功损耗最小、电压质量最优、电压与额定电压值偏差最小、无功补偿设备投资最小、变压器分接头和电容器投切次数最少等[5]。其中使有功损耗最小是最有效的目标函数,也是进行各种无功分配、电压控制的基础,定义形式如下:
(1)
其中:PLoss为系统的有功损耗;NE为总的支路数;gk为支路k的电导;Ui为负载节点i的电压幅值;θij为负载节点i与j之间电压的相位角。
1.2 构建搜索空间
电力系统的无功功率主要来源于发电机、补偿机与调压变压器等设备的感抗做功。因此选取发电机的端电压、有载调压变压器分接头的档位和投入的无功补偿设备的容量作为系统优化的输入变量。无功优化既包含离散变量又有连续变量,其表现为非线性,因此在选择优化算法时需要着重考虑控制变量的表示方式,这对数学模型的建立以及最终的算法效果都有直接影响。
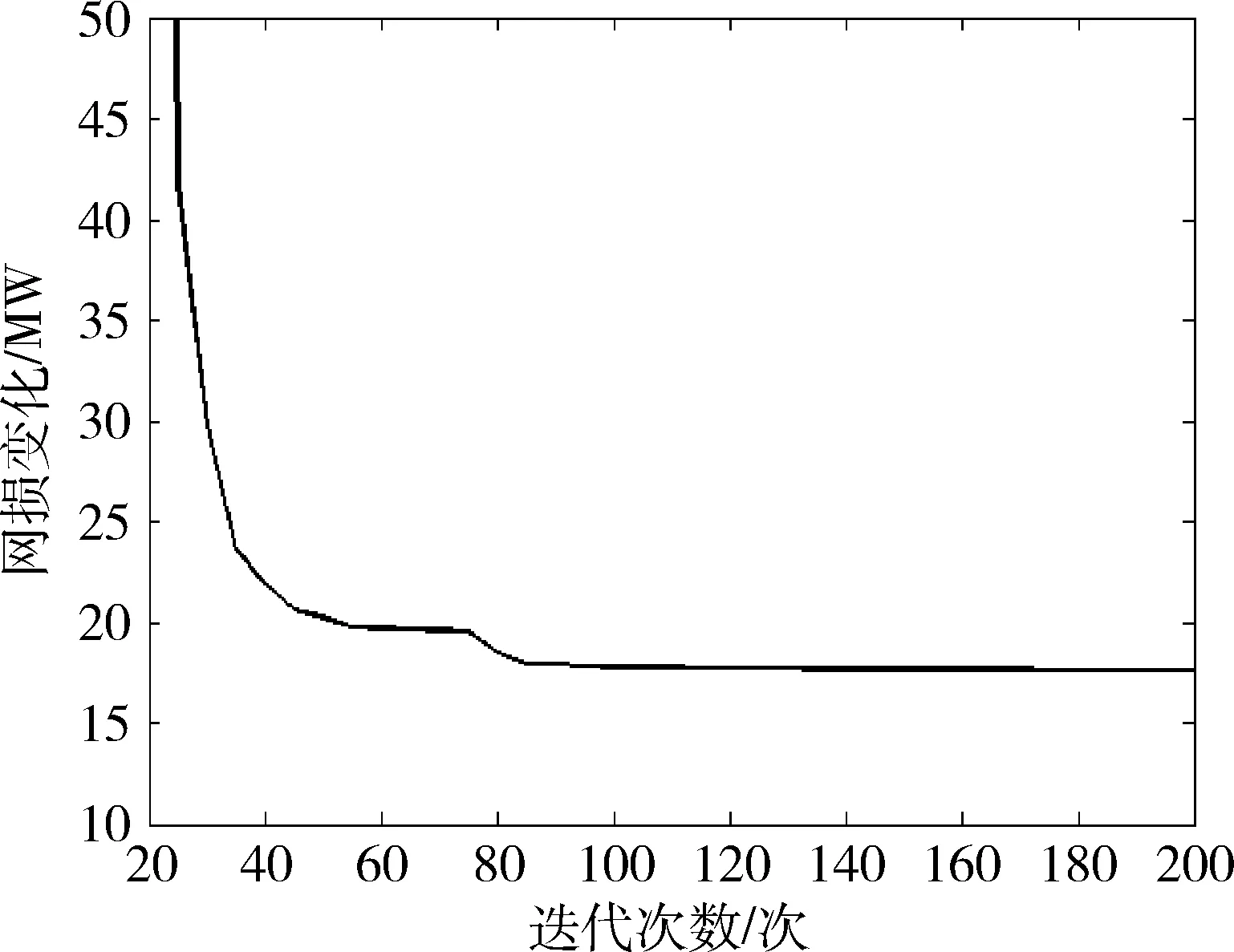
在粒子群优化算法中,每个粒子i都具有N维的位置向量Xi=(x1,x2,…,xN)与飞行速度向量Vi=(v1,v2,…,vN),同时还有由目标函数决定的适应值[5-6]。此时每个X代表一个潜在的解,位置向量的约束条件就构成了算法的搜索空间[7]。因此在无功优化中,以造成无功功率的发电机电压VG、可调变压器变比Ti和补偿电容组数QC构建粒子的位置向量,对于整个系统视为一个粒子,则:
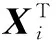
(2)
其中,NG是发电机节点的数目;NT是可调变压器数;NC是无功补偿设备数目,由实际应用系统类型决定。
2 粒子群算法无功优化
本文采用基于惯性权重的粒子群算法求解无功优化问题,粒子群优化算法用于电力系统无功优化的过程及流程如图1所示。

图1 粒子群算法的无功优化流程图
初始化粒子群:以发电机节点电压的上下限、无功补偿设备容量的上下限、变压器分接头上下限等构成解的可行域。在可行域内随机构建n个M维粒子。由上文可知,粒子的位置向量Xi的维度等于控制变量的数量,即:
M=dem(Xi)=NG+NT+NC
(3)
网损值计算:利用式(1)评价每个粒子在当前位置的适应度,即对随机产生的n个粒子分别进行潮流计算,得到对应有功网损,并判断是否满足节点电压及发电机无功出力等约束。
更新粒子的极值:对于每个粒子,存在两个极值:局部极值pBest与全局极值gBest。pBest为单个粒子迭代t0次后最佳的位置值,在本算法中即为最优适应度(最小有功网损)对应的位置X;gBest为对于全体n个粒子,迭代t1次后得到的最优适应度。对于单个粒子,若t0+1次迭代得到的适应度满足:
minPLoss(t0+1) (4) 则更新pBest;对于全体粒子,在第t1+1次迭代后任一粒子出现 minPLoss(t1+1) (5) 则更新gBest。最终获得的minPLoss即为全局最优解。 粒子位置与速度的更新:本文采用基于惯性权重的粒子群算法,引入惯性权重ω。则粒子位置与速度更新由式(6)给出: Vi=ω·Vi+c1·rand()·(pBesti-xi)+ c2·rand()·(gBesti-xi) (6) xi=xi+Vi (7) 其中,c1、c2为学习因子,在本文中,研究惯性权重ω,为简化计算,取c1=c2=2。rand()为介于(0,1)之间的随机数。 为了验证算法的正确性,以有功网损最小为目标函数,综合考虑基于发电机无功功率、电压质量而建立的无功优化模型的可行性和有效性,本文利用MATLAB软件对 IEEE-30标准节点系统初始潮流分布情况进行了分析,结合粒子群算法编写无功优化计算程序进行无功优化测试,并将无功优化结果与初始潮流分布进行比较。保证各节点电压、发电机无功功率在约束条件下,系统的有功网损最小。 3.1 IEEE-30标准节点系统仿真环境设置 IEEE-30标准节点系统分布如图2所示。有6台发电机(节点1为平衡节点,节点2、5、8、11、13为PV节点),其余节为PQ节点,41条支路(其中4条为变压器支路),4台变压器T1、T2、T3、T4,对应节点分别为(6-9)、(6-10)、(4-12)、(27-28)。3个无功补偿节点(节点3、10和24)。发电机端电压的上下限为0.94~1.06,变压器变比上下限为0.9~1.1。 图2 IEEE-30节点系统分布图 节点系统初始情况下,设置发电机的端电压和变压器的变比均为1.0(p.u),无功功率补偿投切量设置为0。通过潮流计算得到:发电机功率P=304.28 MW,Q=174.49 Mvar,系统网损PLoss=20.88 MW,QLoss=81.02 Mvar。 根据粒子群优化算法参数研究,本文所需参数设置如下:粒子群规模为30,加速系数c1和c2分别取2,惯性权重ω选择线性减小的方式取值,最大迭代次数为200。以到达最大迭代次数为一次优化运算的结束条件,重复计算20次作为系统的终止条件,这样可以提高算法计算的准确性。IEEE-30节点系统节点和支路数据、发电机的无功功率约束参数见表1(部分)。 表1 IEEE-30节点系统参数(部分) 3.2 优化结果记录与分析 由运算结果可知,各控制变量取值均在约束条件内,状态变量及网损优化情况比较理想。IEEE-30节点测试系统PSO_ω算法收敛情况如图3所示(PSO_ω为基于惯性权重的粒子群算法程序,输入参数为控制变量个数、控制变量取值范围、迭代次数和种群数量信息),由曲线可得:运算迭代100次后开始收敛,并在140次后网损趋于稳定值。重复20次后得到记录稳定值变化情况,最终取最优值为网损最小值,即17.516 9 MW。 图3 网损收敛曲线 发电机无功功率情况见表2,由发电机的无功出力上下限和无功优化前后的取值可知,第一台发电机初始无功出力越限,第二台发电机无功出力为出力最大值。经粒子群算法优化后所有发电机的无功出力均得到合理分配并在该发电机要求的范围内,这样可以提高设备利用率,使系统运行更加稳定、经济。 表2 发电机无功功率比较 3.3 不同参数取值下的优化情况 为了评估粒子的数目对优化结果的影响,在保持其他参数不变的情况下(重复次数10次),使用不同的粒子数目进行优化。统计结果如表3所示。从表中的结果可知,随着粒子群规模的增长,其平均值即平均网损逐渐减小,收敛性能得到提高,但其寻找最优解的效果并不是很明显,同时其优化的时间也相应地增加。因此针对不同的问题应合理地选取粒子数目,以提高优化效率。 表3 不同粒子数目目标函数变化 由多次仿真优化运行结果可得,在迭代140次后目标函数最优值收敛于稳定值,即PLoss=17.516 9 MW,初始网损为20.88 MW,优化后网损率下降16.11%,且各节点电压和发电机节点无功功率均未越限,节点系统潮流分布得到优化。该优化算法能够有效地寻得最优值,使得有功网损明显降低,最优值与最差值的变化范围较小,并显示出该优化算法具有较好的收敛性、稳定性和鲁棒性。而由于无功优化是复杂的、具有多变量的问题,同时粒子群算法的有效性是通过数值试验和一些实例得到,算法中参数的选取没有一个确定的方法或者公式,因此对算法的收敛性和模型都需要进行更加深入的研究,参数惯性权重的取值有待进一步的探讨。 [1] 许文超,郭伟.电力系统无功优化的模型及算法综述[J].电力系统及其自动化学报,2003,15(1):100-104. [2] 李丽英,周庆捷,杨少坤.电力系统无功优化问题研究综述[J].电力情报,2002,3(6):69-74. [3] 张文,刘玉田.自适应粒子群优化算法及其在无功优化中的应用[J].电网技术,2006,30(8):19-24. [4] 王凌,刘波. 微粒群优化与调度算法[M]. 北京:清华大学出版社,2008. [5] 袁晓辉,王乘,张勇传,等. 粒子群优化算法在电力系统中的应用[J]. 电网技术, 2004,28(19):14-19. [6] 刘世成,张建华,刘宗岐.并行自适应粒子群算法在电力系统无功优化中的应用[J].电网技术,2012,36(1):108-112. [7] 陈前宇,陈维荣,张雪霞,等.基于改进PSO算法的电力系统无功优化[J].电力系统及其自动化学报,2014,26(2):8-13. The reactive power optimization of power system based on particle swarm optimization Lu Jing1,2, Tuo Xianguo1,2, Peng Guili2,3 (1. School of Automation & Information Engineering, Sichuan University of Science & Engineering, Zigong 643000, China;2. School of Information Engineering, Southwest University of Science and Technology, Mianyang 621010, China;3. School of Control and Mechanical Engineering, Tianjin Chengjian University, Tianjin 300384, China) Implementation of reactive power optimization can improve power grid reactive power distribution. A reasonable reactive power distribution can not only guarantee the voltage quality, but also effectively reduce the active power loss which directly influence the safety and stabilization of the power system and even has direct relation to the economy benefit. In this paper,we research the power system reactive power optimization based on inertia weight particle swarm optimization (PSO) algorithm. We establish the out-of-limit issue by using minimum-network-loss as objective function and importing the penalty function to load node voltage and generators reactive power. And establish the power system reactive power optimization simulation program for an IEEE-30 nodes system. The results show that the algorithm can acquire the global optimal solution and the optimized network loss rate reduced by 16.11%. reactive power optimization; particle swarm optimization; network loss; IEEE-30 simulation 国家自然科学基金重大科研仪器设备研制专项(41227802) TM743 A 10.19358/j.issn.1674- 7720.2017.13.007 陆景,庹先国,彭桂力.基于粒子群算法的电力系统无功优化[J].微型机与应用,2017,36(13):19-21,25. 2017-02-14) 陆景(1988-),通信作者,男,在读博士生,助理研究员,主要研究方向:控制理论及应用。E-mail:lujing_017@live.cn。 庹先国(1965-),男,博士,教授,博导,主要研究方向:核地球物理勘探技术、自动化方法。 彭桂力(1981-),男,在读博士生,讲师,主要研究方向:自动控制理论、电工电子仪器仪表的开发研制。3 IEEE-30节点系统算例仿真分析



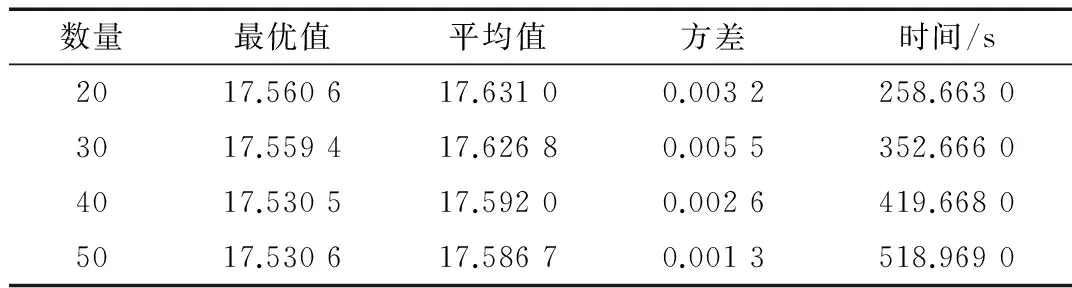
4 结论
