单分子荧光共振能量转移数据处理的优化算法∗

吕袭明1)2) 李辉1)† 尤菁1)2) 李伟1) 王鹏业1)2) 李明1)2) 奚绪光窦硕星

1)(中国科学院物理研究所,软物质物理重点实验室,北京凝聚态物理国家实验室,北京 100190)

2)(中国科学院大学物理科学学院,北京 100049)

3)(西北农林科技大学生命科学院,杨凌712100)

单分子荧光共振能量转移数据处理的优化算法∗

吕袭明1)2) 李辉1)† 尤菁1)2) 李伟1) 王鹏业1)2) 李明1)2) 奚绪光3)窦硕星1)2)‡

1)(中国科学院物理研究所,软物质物理重点实验室,北京凝聚态物理国家实验室,北京 100190)

2)(中国科学院大学物理科学学院,北京 100049)

3)(西北农林科技大学生命科学院,杨凌712100)

(2016年12月8日收到;2017年3月14日收到修改稿)

单分子荧光共振能量转移(smFRET)技术是当今单分子生物物理研究领域的重要实验手段,该技术通过测量供体、受体荧光光强以及二者间的共振能量转移效率,揭示标记位点间的距离,用于研究DNA、蛋白质等生物大分子的构象变化.然而,当前传统数据处理方法大量依赖人工干预,噪音大,严重影响了实验效率和数据的可靠性.本文提出了一种针对smFRET数据的自动分析算法.该算法主要包括三个部分:基于计算供体与受体荧光光强的相关系数来确定受体与供体对应荧光点的自动匹配算法、甄别错误点的筛选算法以及基于隐马尔可夫模型的全局拟合算法.经改进后的算法大大简化了传统算法中需要人工干预的步骤,而且自动筛除了实验数据中主要的几类噪音.将改进的算法应用于人类端粒重复序列G-四联体(G4)DNA折叠动力学的数据分析,结果显示优化算法比传统算法能够更快地得到更高信噪比的数据,而且该数据结果清晰地表明G4的折叠体现出多态性并受到钾离子浓度的影响.

单分子荧光共振能量转移,数据处理算法,G-四联体DNA,折叠动力学

1 引言

随着生物物理学和单分子生物技术的发展,更多的生命科学问题可以在单分子尺度上加以研究.单分子荧光共振能量转移(single-molecule fl uorescence resonance energy transfer,smFRET)技术作为当前单分子生物物理学领域的热门技术,可以实时地观测研究许多生物大分子的构像变化、生物大分子之间的相互作用等过程,从而直观地说明各种生物物理学中的结构与动力学问题[1−5].然而,由于实验中使用的标记荧光分子的不稳定性和单分子生物实验流程的复杂性,smFRET实验发展之初往往难以获得高信噪比的实验数据,实验的重复性也较差.为了解决上述问题,前人进行了种种尝试,解决了荧光分子容易淬灭和闪烁的问题[6−8]、规范了实验操作的步骤[9]、提出了数据处理的理论基础并开发了相应的数据处理程序[10].然而,这些已有的smFRET数据处理算法依赖人工建立坐标匹配关系,容易引入错误配对及不活跃的点,精度差且人为主观因素大,而且拟合EFRET-t曲线时也必须对每条数据曲线分别进行操作,自动化程度低.

针对以上问题,我们对传统处理算法提出了优化.首先,利用smFRET数据中供体(donor)与受体(acceptor)荧光变化曲线的负相关特性实现了供体与受体荧光点坐标对应关系的自动确立.其次,利用该负相关性对数据进行自动筛选,可有效筛除杂质发光或荧光提前淬灭等情况.最后,通过改进隐马尔可夫模型(hidden Markov model,HMM)在数据拟合过程中的运用方式,实现一次性全局拟合所有EFRET-t曲线,省去人工分别拟合再整合的麻烦.经过改进的数据处理算法大大提高了实验数据的可靠性,自动化的处理方式帮助处理大批量的实验结果,有效提高了实验效率以及实验的可重复性.

2 算法原理

2.1 smFRET原理及荧光分子光强的负相关性

供体荧光分子在受到外源激光激发后发出荧光,该荧光的波谱与受体荧光分子的激发波谱交叠,若此时受体与供体的距离足够接近,则供体荧光光能会部分传输至受体,使其受激发出荧光.假设供体荧光光强为ID,受体光强为IA,则能量传递的效率.考虑到供体荧光泄漏、受体荧光分子直接发光等因素的影响,该公式最终被修正为,γ为修正因子[9,11,12].根据已有研究,该效率与两荧光分子的距离R具有如下关系:,其中常数R0为Förster半径[9,13].由此可知,通过观测标记在同一生物大分子上的一对供体受体荧光分子实时的荧光光强变化,计算EFRET便可获知两个荧光分子标记位点间距离R的变化信息,从而反映出生物大分子的结构变化.

需要注意的是,在实验中外源激发光强度相对恒定,根据能量守恒,ID与IA应满足负相关关系,ID-t曲线与IA-t曲线的相关系数

(xi,yi分别为ID与IA的序列)应当为负,且该负相关关系符合得越好,r应当越接近−1.

2.2 HMM拟合原理

马尔可夫过程是指在已知当前状态的情况下,未来的演变不依赖于其过去演变的随机过程.处于平衡状态下生物大分子的不同状态间的跳转概率恒定,下一状态仅与当前状态有关,故其态跳转过程属于马尔可夫过程[10].HMM是用来描述含有隐含参量的马尔可夫过程,对于smFRET实验来说,EFRET值是显性变化的参量,而大分子实际所处状态则是隐含变化的参量,需要通过拟合分析得到.如图1中的original曲线为原始EFRET-t曲线,由于实验中不可避免的噪音,EFRET值在一定范围内波动,某时刻的EFRET值到底对应大分子的哪一个结构具有不确定性.HMM拟合算法通过计算所有可能路径的概率的最大值,将实验中在0到1之间连续变化的EFRET-t曲线拟合为在若干分离EFRET值之间跳转的EFRET-t方波(如图1中的squared曲线),从而确定平衡状态下生物大分子处于各种结构时EFRET的准确高度以及EFRET变化的起止时间.

图1 EFRET-t曲线(original)与其方波拟合曲线(squared)Fig.1.EFRET-t curve and the square-function fi tting curve.

下面以穷举法HMM拟合两态EFRET-t曲线为例来说明HMM拟合的原理.首先对EFRET-t曲线中EFRET做柱状分布图并使用多峰高斯拟合,此步需要人工输入态数目并给出态位置的初值,设拟合后两态S1与S2(这两态被称为隐状态)的高斯峰中心位置(称为态位置)分别为E1与E2,相应标准差为σ1与σ2,EFRET-t曲线上A点EFRET为EA,此值被称为观测值,则隐状态为S1时观测值为EA的概率,同理可得q(AS2),这些概率称为测量概率.另外定义pij为相邻两帧之间从Si态跳转到Sj态的概率(i,j可相等),这样可得一个态间跳转概率矩阵,称为转移矩阵.然后穷举EFRET-t曲线所有可能的隐状态路径并通过观测概率与转移矩阵计算每种路径的总概率大小,其中总概率最大值的情况即为最终拟合路径.由于转移矩阵未知,所以需要通过拟合结果来逐步迭代获得.

以上使用穷举法来简单解释HMM拟合过程.在实际运用中,通常使用一种HMM简化算法,即Baum-Welch算法,来拟合得到转移矩阵、高斯峰中心、标准差以及该算法引入的初始概率.使用Baum-Welch算法可以对一系列具有相同隐状态的观察序列进行统一的参数学习,然后再使用Viterbi算法即可对每一条观察序列的路径进行拟合[14].

3 实验条件

smFRET光路如图2所示.波长为532 nm的激光激发反应池中被标记物上的供体荧光分子(Cy3),供体荧光分子转移部分能量到受体荧光分子(Cy5),两者发出的荧光经分光光路分为中心波长在568和675 nm的平行两束,后被EMCCD(DU897,Andor)收集.供体与受体荧光点的信号分别成像于CCD视野的左右半区,通常需要实验后根据其坐标对应关系将来自同一被标记物上的供体与受体荧光点匹配.

图2 smFRET系统示意图Fig.2.Schematic of the smFRET system.

为探究人类端粒上的DNA重复序列G-四联体(G4)结构在K+溶液中的折叠动力学.在G4的首尾段分别标记供体(Cy3)和受体(Cy5)荧光分子.然后在10 mM/100 mM KCl(M=1 mol/L),10 mM Tris-HCl,pH 7.5缓冲液(下称K+缓冲液)环境中测量G4上荧光分子的smFRET信号,并使用优化算法处理实验结果.已知G4在K+溶液存在条件下有多个折叠状态[15−18](如图3),统计EFRET柱状分布图与转移矩阵后可得到更加详细的结构与动力学信息.实验操作为:使用K+缓冲液冲洗固定有biotin-PEG与mPEG的反应池,加入10µg/mL的链霉亲和素(streptavidin)溶液,等待其与生物素(biotin)连接5 min,再次用K+缓冲液冲洗反应池后加入含有G4的K+缓冲液,其中G4浓度为10 pM.待G4与反应池表面连接30 s后用含有除氧抗淬灭系统[19,20](2.3 mg/mL葡萄糖(glucose),0.1 mg/mL葡萄糖过氧化酶(glucose oxidase,Sigma),0.02 mg/mL过氧化氢酶(catalase,Sigma),1 mM Trolox(Sigma))的K+缓冲液冲洗反应池后放置在显微镜载物台上开始荧光观察录制.

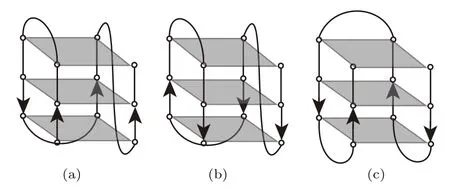
图3 人类端粒DNA重复序列G4在K+溶液中的多种折叠结构(a)3+1混合1型结构;(b)3+1混合2型结构;(c)椅式结构Fig.3.Di ff erent folding conformations of human telomeric G4 in K+solution:(a)3+1 hybrid form 1;(b)3+1 hybrid form 2;(c)chair conformation.

4 smFRET数据处理方法

当前,smFERT数据处理方法主要采用人工确定坐标对应关系,缺少对错误点的筛选过程,使用HMM算法拟合单条EFRET-t曲线后再汇总拟合全局.其中Ha作为smFRET领域的先驱,提出了使用HMM算法拟合EFRET-t曲线的方法,开拓了一种较为普遍使用的分析方法[10].这些传统方法在数据提取、筛选与拟合步骤上都过于依赖人工处理,具有精度低、工作量大、人为主观因素影响大等缺陷,需要改进.

下面将在数据提取、数据筛选以及数据拟合三个方面分别介绍优化的自动分析算法,并使用优化算法处理G4的smFRET实验数据,分析实验结果.

4.1数据提取

经过显微镜成像的分光光路后,smFRET的供体与受体荧光点会分置于所录制图像的左右半区.为了将同一生物大分子上供体与受体的荧光点对应起来,需要建立两者的坐标对应矩阵.传统方法是通过在录像叠加图像上根据左右半区形貌的相似性,人工选取三对对应的供体、受体荧光点来计算坐标变换矩阵,该方法精度差且效率低,光点密集时尤其如此.

根据原理中介绍的ID与IA的负相关性,我们提出以下算法以便自动准确确定参考点:以512×512像素实验录像为例,首先叠加原始实验录像获得平均图像并对其降噪,找出平均图像上的所有光点,记录其坐标,并从原始实验录像中提取相应位置光强随时间变化的曲线.任取左侧某一供体分子,坐标为(xd,yd),求其ID-t曲线与在右侧大致对应范围(xd+256±5,yd±5)内各个受体分子IA-t曲线的相关系数r.若发现其中出现r小于一定阈值r0时(如800帧录像时r0可取−0.5),我们认为该对荧光信号高度负相关,为同一生物大分子上正常发生smFRET的一对供体与受体分子发出,记录该供体与受体坐标作为一对参考点.重复找到三对不同参考点后(三对点最好在图像上分散)即可得到坐标变换矩阵,多次重复以上过程可确保准确.上述过程可由程序自动完成,而且即使不同实验中重新调整分光光路,坐标对应关系发生改变,也可自动生成新的坐标对应矩阵而不用重新人工校准.利用该坐标变换矩阵即可计算匹配所有光点的对应点,供下一步数据筛选.

使用上述优化算法前后的结果比较如图4.传统方法计算坐标对应矩阵时三对参考点由实验者人工选点确立,但由于smFRET图像光点密集,单从图像左右半区形貌相似性上判断参考点,如果出现误差将会得到错误的坐标对应矩阵,从而在后续的匹配中引入错配的情况.如图4(a)中,供体(Cy3)与受体(Cy5)的光强变化并不呈现FRET应有的负相关关系.而使用我们改进的方法,依照相关系数r自动寻找参考点并计算对应关系后,可得到同一供体分子(42,172)的正确受体分子位置(297,176),如图4(b).可以发现,正确与错误受体坐标仅在横坐标相差3个像素,使用传统算法在人工点选时若出现误差很容易导致坐标对应矩阵计算错误,最终导致错误匹配.采用优化后的算法则可根据发生高质量smFRET的数据点自动计算坐标对应矩阵,即使在实验光路频繁调整、坐标对应关系变动的情况下依然能自动保证匹配准确.

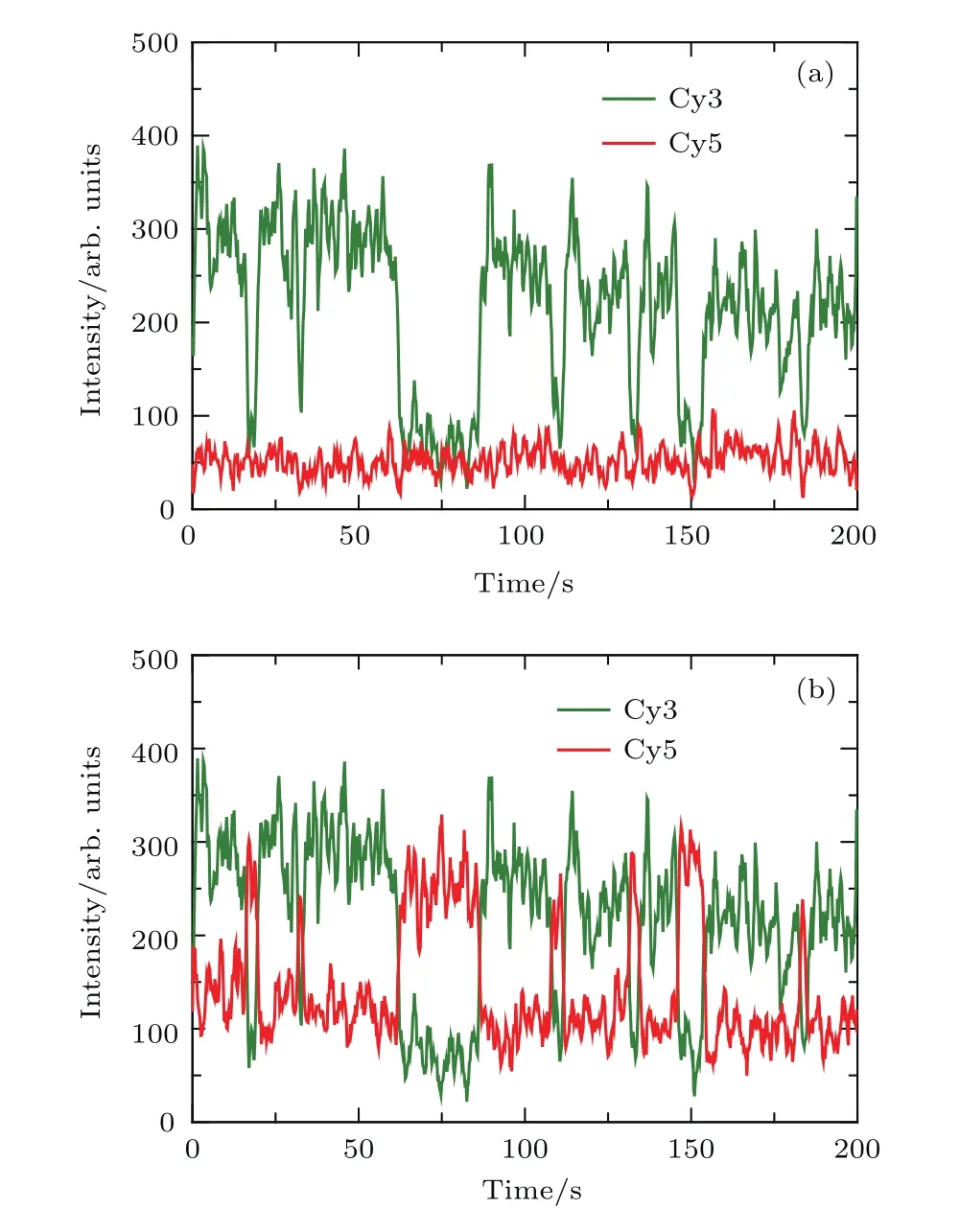
图4 坐标对应算法结果对比(a)传统方法可能产生的错配,供体坐标为(42,172),受体坐标为(300,176);(b)优化方法修正后正确配对,供体坐标为(42,172),受体坐标为(297,176)Fig.4.Comparison of fi lm mapping algorithms:(a)Mismatch caused by traditional algorithm,donor coordinate(42,172),acceptor coordinate(300,176);(b)correction made by the advanced algorithm,donor coordinate(42,172),acceptor coordinate(297,176).

4.2 数据筛选

采用正确坐标对应关系提取的数据并不都是高质量的smFRET数据,其中可能包含杂质发光、供体荧光分子过早淬灭等情况,相应的EFRET-t曲线不能真实反映生物大分子的状态变化,需要进行筛选.传统方法对于获得的荧光信号不能进行高效准确的筛选,导致数据质量不高或者人为因素影响大.经我们优化后的算法将对数据进行自动筛选.同样依据ID与IA的负相关性,我们计算ID-t曲线与IA-t曲线的相关系数r,通过设置阈值来去掉r过大的情况.图5为同一实验录像中的三种典型荧光光强数据,录像帧数均为800帧.图5(a)中r=0.09,供体与受体光强无相关性且光强在长时间内几乎不变,可能为溶液中的杂质受激发光或被标记物失去生物活性.图5(b)中r=−0.3,供体与受体光强在约80 s前具有显著负相关性,说明该处确实有正确标记的生物大分子.但在80 s后,供体分子光强曲线下降(绿色)但受体分子光强(红色)并未上升,说明并未发生能量传递,而是供体分子发生了荧光淬灭,80 s之后的EFRET-t曲线不能反映生物大分子的状态变化,该数据也需要筛除.图5(c)中r=−0.9,ID与IA的负相关性全程显著,为优质数据,需要保留.经过测试,对于800帧的数据,将阈值r0设为−0.5,自动筛选保留r<−0.5的ID-t曲线与IA-t曲线数据,将能得到高信噪比的实验结果.

图5 不同相关系数r的荧光光强数据(a)r=0.09;(b)r=−0.3;(c)r=−0.9Fig.5.Fluorescence intensity traces with di ff erent correlation coefficient r:(a)r=0.09;(b)r=−0.3;(c)r=−0.9.

图6 EFRET柱状分布图对比(a)不使用相关系数r进行数据筛选;(b)使用相关系数r进行自动数据筛选Fig.6.Comparison of histograms of EFRET:(a)Output without data sifting by the correlation coefficient r;(b)Output using data sifting by the correlation coefficient r.

为证明使用相关系数r自动筛选荧光光强数据的算法不仅高效、客观,并可有效提高实验结果的信噪比,充分利用实验数据,我们给出对同一次实验录像不使用与使用该优化算法得到的EFRET柱状分布图的结果对比(EFRET-t曲线通过ID-t与IA-t曲线可得).该实验中,首尾荧光标记的人类端粒G4在100 mM KCl,10 mM Tris-HCl,pH 7.5溶液的环境中测量smFRET信号.图6(a)为使用传统方法而不使用相关系数r进行数据筛选的结果.传统方法为防止出现如图5(b)中供体过早淬灭的情况,对所有数据均只选取前若干帧的平均EFRET值做柱状图,浪费了图5(c)情况下后半段大量有效的EFRET值信息,使得结果数据量少.同时,如果传统算法不对所有的光强曲线进行人工筛选,则无法排除图5(a)的情况.综合以上因素,传统方法所得到的图6(a)中柱状图噪音大,数据量少.图6(b)为使用相关系数r进行数据筛选的结果.由于弥补了传统方法的不足,排除了图5(a)和图5(b)所示的两种主要噪音来源,同时充分利用了高质量数据,最终得到数据量大、高斯峰清晰的EFRET值分布图,提高了实验效率与准确性.

我们经优化算法处理之后的实验结果与他人同样的实验结论一致[21],证明该改进算法所得结果准确且高效.关于前人结果中EFRET=0的受体荧光淬灭与闪烁的数据如何去除,我们将在后面的数据拟合过程中讨论.

4.3 数据拟合

得到ID-t与IA-t曲线数据后可计算得到EFRET-t曲线,为了进一步分析平衡态下生物大分子的各种结构以及结构间相互转换的规律,需要将连续变化的EFRET-t曲线拟合为在几个分离EFRET值之间跳转的方波曲线.前人已经提出并使用HMM模型来拟合EFRET-t曲线,然而传统方法为先对每条EFRET-t曲线单独进行拟合,再将这些拟合结果进行汇总再拟合.由于每一条曲线可能会呈现不同的态数目和态位置,所以单独拟合时需要分别输入态数目和态位置.这样拟合完成同一平衡条件下所有EFRET-t曲线后需要再次整合态位置等参数.整个过程需要大量的人工参数输入,费时费力.

使用我们优化的方法可以避免这个问题:首先用Baum-Welch算法对同一平衡状态下的所有EFRET-t曲线进行全局的参数学习拟合.由于同一平衡条件下转移矩阵恒定,且所有分子对应相同的隐状态,因此对所有EFRET-t曲线进行统一的参数学习拟合可以直接得到分子所共有的不同态的高斯峰中心位置以及不同状态间的跳转概率.然后将得到的全局态位置和跳转概率配合Viterbi算法对每一条EFRET-t曲线进行路径的拟合.这样的拟合过程只需要对态数目和态位置的初值进行一次设定,就可完成对所有同一平衡状态下EFRET-t曲线的全局拟合,不仅高效而且准确.

我们使用优化后的拟合程序拟合了G4在100 mM K+溶液条件下的229条EFRET-t曲线,输入一次态数目与位置初值数据(4态,EFRET初值分别为0,0.3,0.6,0.8)得到4态的最终位置分别为:0,0.33,0.59,0.77.

需要注意的是,经过数据筛选步骤得到的EFRET柱状图中,EFRET=0的峰实际对应供体荧光淬灭或闪烁的状态.在数据拟合完成后,我们可根据拟合结果进一步筛除该态的EFRET数据,得到最终的柱状分布图如图7(a).再对剩下的3态跳转概率重新归一化,就可得到实际的态跳转概率从而进一步计算平衡相关参数.筛除供体荧光淬灭或闪烁状态后,G4在100 mM K+溶液条件下的拟合结果共有3态(如图7(a)),其中未折叠态(EFRET=0.33)平均寿命为5.4 s,两种混合型折叠构型(如图3(a)和(b),EFRET=0.59)平均态寿命为10 s,反平行折叠构型(如图3(c),EFRET=0.77)平均态寿命为51 s.同样方法处理G4在10 mM K+溶液条件下的119条EFRET-t曲线数据(如图7(b)),也得到3态,其中未折叠态(EFRET=0.25)平均寿命为15 s,两种混合型折叠构型(如图3(a)和(b),EFRET=0.57)平均态寿命为10 s,反平行折叠构型(如图3(c),EFRET=0.77)平均态寿命为31 s.我们的结果表明,K+对于G4的折叠能起到稳定的作用.以上结论与通过传统方法拟合得到的结果一致,但是我们的算法获得了更加清晰的状态特征峰[21,22].

图7 去除受体荧光淬灭与闪烁后的EFRET柱状分布图(a)100 mM K+溶液条件;(b)10 mM K+溶液条件Fig.7.Histograms of EFRET.EFRET-t curves that exhibited acceptor bleaching and blinking are excluded:(a)100 mM K+;(b)10 mM K+.

我们优化后的算法使用Baum-Welch算法对所有EFRET-t曲线进行全局的参数学习,再用全局参数对每条EFRET-t曲线进行路径拟合,既减少了人工操作的步骤又保证了拟合结果准确.而且,通过拟合结果可将受体荧光分子淬灭与闪烁的状态进行有效筛除,让G4的未折叠态与各折叠态更加明显,最终结果更加精确.

5 结论

针对传统smFRET数据处理算法在数据提取、筛选和拟合方面的不足,我们提出了一种优化算法.运用smFRET的原理,首先引入相关系数r来判定图像上两荧光点是否为同一生物大分子上的供体、受体的荧光标记,自动寻找实验数据两通道的坐标对应关系,使得该步骤不再依赖人工,提高了精度与效率.然后,在数据筛选过程中,通过相关系数r来自动判定并筛除杂质发光、被标记物无活性以及供体荧光分子淬灭等错误数据干扰,提高了数据质量的同时避免了人工筛选的低效和人的主观倾向性.最后,通过使用Baum-Welch算法先对同一平衡条件下的所有数据进行全局拟合,然后使用全局拟合参数对单条数据单独拟合路径,从而获得态位置、态平均寿命,减少了HMM拟合EFRET-t曲线中的人工操作环节,提高了数据处理效率.由拟合路径可对受体荧光的淬灭与闪烁数据进行筛除,进一步提高了数据的信噪比,为后续分析实验结果提供了便利.

我们将该算法应用于G4折叠动力学数据的处理,得到了清晰的EFRET柱状分布图,展现出G4的未折叠态与两个折叠态,并获得了不同状态下的平均寿命,进一步揭示了G4的折叠的多态性以及各态在不同K+溶液条件下的稳定性变化.日渐成熟的smFRET实验技术已经向着高精度、高通量的方向发展,相信更多自动化的数据处理算法将会在其中起到重要的作用.

[1]Zhou R,Kozlov A G,Roy R,Zhang J,Korolev S,Lohman T M,Ha T 2011 Cell 146 222

[2]Honda M,Park J,Pugh R A,Ha T,Spies M 2009 Mol.Cell 35 694

[3]Liu C,Mckinney M C,Chen Y H,Earnest T M,Shi X,Lin L J,Ishino Y,Dahmen K,Cann I K,Ha T 2011 Biophy.J.100 1344

[4]Wu J Y,Stone M D,Zhuang X 2010 Nucl.Acids Res.38 e16

[5]Hengesbach M,Kim N K,Feigon J,Stone M D 2012 Angew.Chem.51 5876

[6]Ha T,Tinnefeld P 2012 Annu.Rev.Phys.Chem.63 595

[7]He Z C,Li F,Li M Y,Wei L 2015 Acta Phys.Sin.64 046802(in Chinese)[何志聪,李芳,李牧野,魏来2015物理学报64 046802]

[8]Li M Y,Li F,Wei L,He Z C,Zhang J P,Han J B,Lu P X 2015 Acta Phys.Sin.64 108201(in Chinese)[李牧野,李芳,魏来,何志聪,张俊佩,韩俊波,陆培祥2015物理学报64 108201]

[9]Roy R,Hohng S,Ha T 2008 Nat.Methods 5 507

[10]Mckinney S A,Joo C,Ha T 2006 Biophys.J.91 1941

[11]Lee N K,Kapanidis A N,Wang Y,Michalet X,Mukhopadhyay J,Ebright R H,Weiss S 2005 Biophys.J.88 2939

[12]Sabanayagam C R,Eid J S,Meller A 2005 J.Chem.Phys.122 061103

[13]Deniz A A,Dahan M,Grunwell J R,Ha T J,Faulhaber A E,Chemla D S,Weiss S,Schultz P G 1999 PNAS 96 3670

[14]Rabiner L R 1989 Proc.IEEE 77 257

[15]Ambrus A,Chen D,Dai J,Bialis T,Jones R A,Yang D 2006 Nucl.Acids Res.34 2723

[16]Gray R D,Trent J O,Chaires J B 2014 J.Mol.Biol.426 1629

[17]Tippana R,Xiao W,Myong S 2014 Nucl.Acids Res.42 8106

[18]Li Y,Liu C,Feng X,Xu Y,Liu B F 2014 Anal.Chem.86 4333

[19]Cordes T,Vogelsang J,Tinnefeld P 2009 J.Am.Chem.Soc.131 5018

[20]Hubner C G,Renn A,Renge I,Wild U P 2001 J.Chem.Phys.115 9619

[21]Lee J Y,Okumus B,Kim D S,Ha T 2005 PNAS 102 18938

[22]Noer S L,Preus S,Gudnason D,Aznauryan M,Mergny J L,Birkedal V 2016 Nucl.Acids Res.44 464

PACS:87.80.Nj,87.15.ad,87.15.Cc,87.15.B–DOI:10.7498/aps.66.118701

An optimization algorithm for single-molecule fl uorescence resonance(smFRET)data processing∗

Lü Xi-Ming1)2)Li Hui1)†You Jing1)2)Li Wei1)Wang Peng-Ye1)2)Li Ming1)2)Xi Xu-Guang3)Dou Shuo-Xing1)2)‡
1)(Beijing National Laboratory for Condensed Matter Physics,Key Laboratory of Soft Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China)
2)(School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China)
3)(College of Life Sciences,Northwest A&F University,Yangling 712100,China)

8 December 2016;revised manuscript

14 March 2017)

The single-molecule fl uorescence resonance energy transfer(smFRET)technique plays an important role in the development of biophysics.Measuring the changes of the fl uorescence intensities of donor and acceptor and of the FRET efficiency can reveal the changes of distance between the labeling positions.The smFRET may be used to study conformational changes of DNA,proteins and other biomolecules.Traditional algorithm for smFRET data processing is highly dependent on manual operation,leading to high noise,low efficiency and low reliability of the outputs.In the present work,we propose an automatic and more accurate algorithm for smFRET data processing.It consists of three parts:algorithm for automatic pairing of donor and acceptor fl uorescence spots based on negative correlation between their intensities;algorithm for data screening by eliminating invalid fl uorescence spots sections;algorithm for global data fi tting based on Baum-Welch algorithm of hidden Markov model.

Based on the law of energy conservation,the light intensity of one pair of donor and acceptor shows a negative correlation.We can use this feature to fi nd the active smFRET pairs automatically.The algorithm will fi rst fi nd out three active smFRET pairs with correlation coefficient lower than the threshold we set.This three active smFRET pairs will provide enough coordinate data for the algorithm to calculate the pairing matrix in the rest of automatic pairing work.After obtaining all the smFRET pairs,the algorithm for data screening will check the correlation coefficient for each pair.The invalid pairs with correlation coefficient higher than the threshold value will be eliminated.The rest of smFRET pairs will be analyzed by the data fi tting algorithm.The Baum-Welch algorithm can be used for learning the global parameters.The global parameters we obtained will then be used to fi t each FRET-time curve with Viterbi algorithm.The global parameter learning part will help us fi nd the speci fi c FRET efficiency for each state and the curve fi tting part will provide more kinetic parameters.

The optimization algorithm signi fi cantly simpli fi es the procedures of manual operation in the traditional algorithm and eliminate several types of noises from the experimental data automatically.We apply the new optimization algorithm to the analyses of folding kinetics data for human telomere repeat sequence,the G-quadruplex DNA.It is demonstrated that the optimization algorithm is more efficient to produce data with higher S/N ratio than the traditional algorithm.The fi nal results reveal clearly the folding of G-quadruplex DNA in multiple states that are in fl uenced by the K+concentration.

smFRET,data processing algorithm,G-quadruplex DNA,folding kinetics

10.7498/aps.66.118701

∗国家自然科学基金(批准号:11674383,11474346,11274374)、国家重点基础研究发展计划(批准号:2013CB837200)和国家重点研究发展计划(批准号:2016YFA0301500)资助的课题.

†通信作者.E-mail:huili@iphy.ac.cn

‡通信作者.E-mail:sxdou@iphy.ac.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.11674383,11474346,11274374),the National Basic Research Program of China(Grant No.2013CB837200),and the National Key Research and Development Program of China(Grant No.2016YFA0301500).

†Corresponding author.E-mail:huili@iphy.ac.cn

‡Corresponding author.E-mail:sxdou@iphy.ac.cn