基于直接边界元法的某型飞行器气动噪声研究

2017-08-09李智劳崔盼礼

环球市场 2017年19期

关键词：偶极子声压级声场

李智劳刘凡崔盼礼郭艳

中国飞机强度研究所

基于直接边界元法的某型飞行器气动噪声研究

李智劳刘凡崔盼礼郭艳

中国飞机强度研究所

飞行器在飞行过程中，其表面受到强大气流的作用，内部或外部会产生很大声场。强大的声场不但会造成飞行器内部的控制设备损坏，还可能破坏飞行器本身的结构。本文主要运用计算流场的软件FLUENT和计算声学的软件Virtual Lab来解决气动声学问题。对于流速小于0.3马赫时的流场，将结构表面的脉动压力转化为结构表面的偶极子，然后计算由偶极子引起的声场分布。本文的研究成果对后续继续研究飞行器气动噪声问题打下了基础，具有重要的工程应用价值。

飞行器；声场；流场；脉动压力；气动声学

1 引言

现代高速弹道导弹在飞行过程中，由于机体上各部件所产生的宽带噪声而引起气流分离流、旋涡、湍流以及其附面层流相互干扰等现象对导弹飞行的气动性能必然产生十分重要的影响，这种影响还产生许多非定常的气动现象，对飞行器表面压力分布产生极大的影响，从而直接关系到导弹的命中精准度甚至其结构安全。因此研究飞行器各部件噪声(包括发动机及其喷流产生的噪声)的产生、发展以及对飞行器的影响和相互作用是对空气动力学界的严峻挑战，同时也是空气动力学与气动声学研究领域的良好机遇。

2 偶极子声源

偶极子声源可以看做是由两个距离很近，振幅相同，相位相差的振动脉动球源组成的，存在于具有较高气流速度的气流场中，其辐射声功率为：

WD是偶极子声源的辐射声功率，其余符号和上式含义相同，上式表明，偶极子声源的声辐射功率与气流流速的六次方成正比。

3 直接边界元理论

Helmhotz方程的边界积分方程为

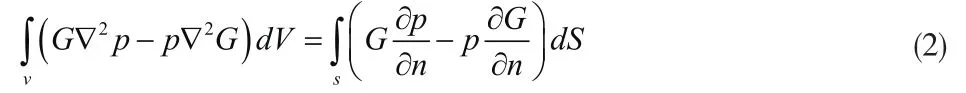
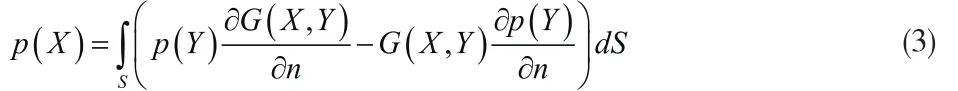
若将Y点移到边界S上，则上式所有的未知量都位于边界上，那么区域V内任一点的p都可以得到：

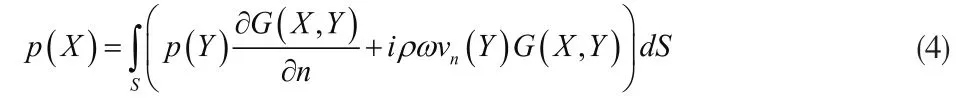
若点X位于面S上，则面σ就是一个半球面，则式(2)简化为

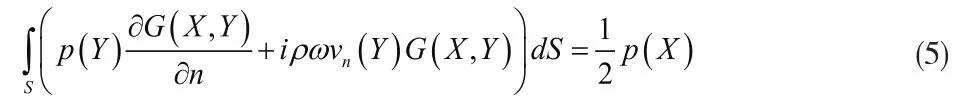
但是振动体表面S通常并不平滑，所以σ也不再是一个半球面。设

可得一般表达式

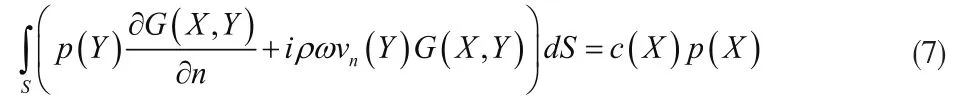
对于内场问题，流体域必须封闭，流体介质位于振动体表面S的相反面内。内场问题的积分方程为：

对于式(7)和式(8)，用解析法求解仍很困难，因此需要在振动体表面上进行离散。

将振动体表面划分为m个单元，包含α个结点，那么，边界上任一点ξ的边界量(压力、法向速度等)就可以利用结点上的边界量通过插值函数(形函数)的形式来表示：

式中，Nα(ξ)为形状函数；pmα为单元m上的结点α的压力；vnmα为单元m上的结点α的法向速度。于是积分公式(7)转化为：

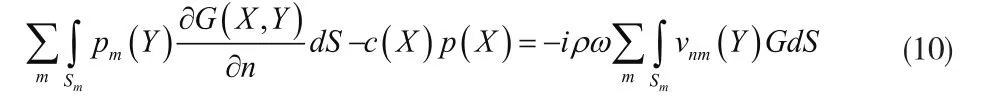
式中，Sm为单元m的面积。通过逐渐逼近点ξ的坐标xi(ξ)，压力pm(ξ)和法向速度，得到下式：

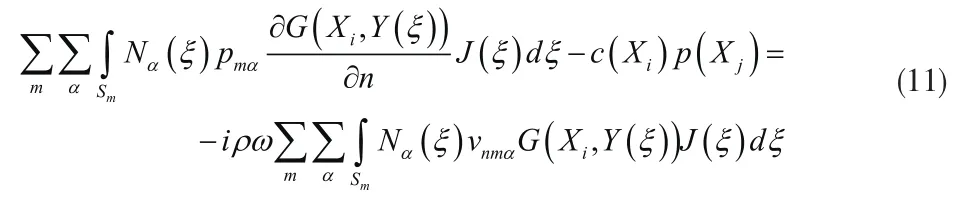
式中，J(ξ)为左边转化的雅可比矩阵。则，表面上一结点J的表达式为：

定义下述影响系数：

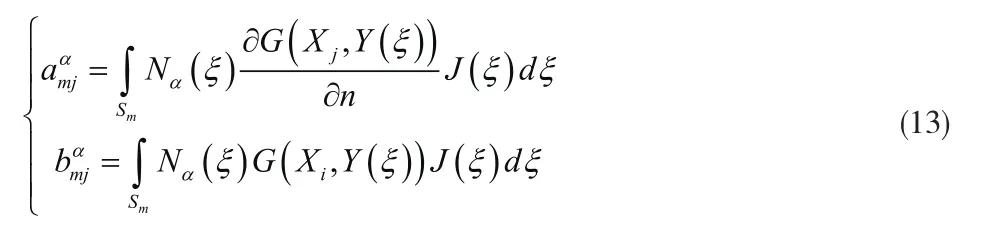
引入全局结点项l，任一单元m和结点α都与之相对应。将影响系数代入式(12)，可得结点l的表达式为

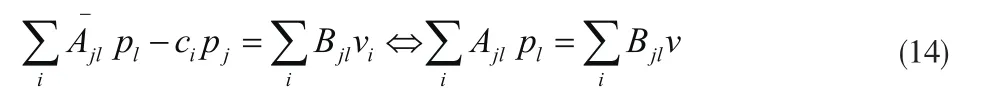
写成矩阵形式：

式中，A、B为影响矩阵；p为流体模型表面上的结点压力向量；vn为流体模型表面结点法向速度向量。声场中任一点X处的声压为：

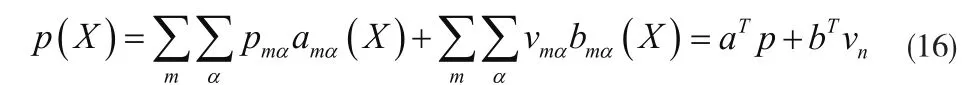
4 算例

4.1 偶极子声源计算

本例中流场流速为0.3马赫。经过实验研究0.3马赫以下，流场中的四极子声源对声压级的贡献可以忽略不计，所以只需要导出飞行器表面的脉动压强。对流场先进行稳态计算，进行若干次循环，当流场稳定以后再进行瞬态计算，并同时记录数据，输出飞行器表面脉动压强，作为飞行器表面偶极子声源。

4.2 噪声计算

本例运用直接边界元法计算气动噪声。所计算的频率为10-5000Hz，声学边界元要求边界元网格最大边长至少应小于声波波长的1/6即：

其中，α为最单元的最大边长，λmin为声波的最小波长，v为空气中的声速，Tmin为最小周期，fmax为计算的最大频率。v=340m/s，计算的最大频率fmax=5000Hz，通过上面的公式，计算得到最大单元边长α=11.333mm，本例计算的单元边长α选为10mm。边界元模型如图1所示，为四边形单元。因为四边形单元在进行数值求解时精度要好于三角形单元。

图1 飞行器边界元网格图

图2 内场点网格图

图3 外场点网格图

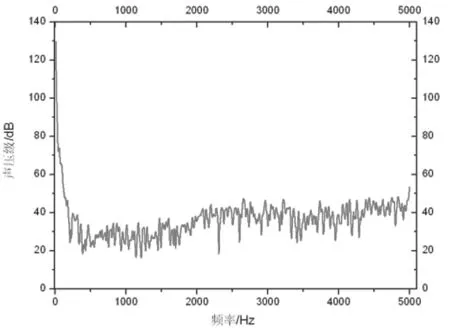
图4 飞行器声压级分布(内场点)

如图2，3所示分别为边界元内外场点网格。内场点的网格是半径为0.015m，长度为1.002m的柱面。外场点的网格是半径为0.5m，长度为4.3m的柱面。其中，内外场点的网格都是四边形网格。

4.3 气动噪声计算及分析

图5 飞行器声压级分布(外场点)

图6 频率为10Hz时飞行器表面声压级分布图

图4为飞行器声压级分布(32场点)，可以看出飞行器内部场点的最大声压级约为129dB，外部场点的最大声压级约为88dB。图6为飞行器表面在频率为10Hz时的声压级分布图。从图6可以看出在频率为10Hz时，声压级最大值为193dB，分布于飞行器头部位置，这是因为气流经过飞行器表面，在飞行器头部产生最大的脉动压强。