一道力学综合题的多种解法

河北 董凤娥

一道力学综合题的多种解法

河北 董凤娥

一题多解是培养学生准确理解和灵活运用物理规律及方法的有效途径，也是培养学生发散思维的方式之一，更是提高复习效率的有效方法。现以一道典型力学综合题为例，说明一题多解在学习中的作用。

【题目】如图1所示，C是放在光滑水平面上的木板，质量为3m，在木板上面有两块质量均为m的小木块A和B，它们与木板间的动摩擦因数均为μ。最初木板静止，A、B两木块同时分别以水平向右的初速度v0和2v0在木板上滑动，木板足够长，A、B始终未滑离木板。求：

图1

（1）木块B从刚开始运动到与木板C速度刚好相等过程中，木块B所发生的位移；

（2）木块A在整个过程中的最小速度值。

【解析】这是一道经典的力学问题，经常出现在考试中，其考查的知识涉及高中力学的绝大多数重点内容，思维发散，非常值得我们研究。

首先，我们分析一下题设条件。光滑水平面意味着对于木板C和木块A、B组成的系统来说，在水平方向上不受任何外力，所以系统动量守恒；又因为木板足够长，A、B始终未滑离木板，这意味着三者最终具有相同的速度v。故有

其次，结合题意可知，在整个运动过程中，小木块A和B与木板C发生相对运动，会受到木板给它们的向左的摩擦力，大小为μmg；而木板受到向右的摩擦力，大小为2μmg。木块A向右做匀减速直线运动，因木块A的初速度小，故木块A的速度首先减小到和木板C具有同样大小的速度，此时它的速度就是在整个运动过程中的最小速度，然后随木板做匀加速直线运动；当木块B的速度也减小到与木板C的速度相同时，此时木块B发生的位移就是第一问要求的位移；然后三者相对静止一起向右做匀速直线运动。木块C可以看成先做两段加速度不同的匀加速直线运动，最后向右做匀速直线运动。

到此，我们不难发现第一问所要求的问题：应该是当B的速度减小到与木板C的速度相同时，即三者从开始相互作用到三者相对静止时，木块B在木板C上发生的相对位移的大小。对木块B运用动能定理，有

第二问所要求的问题是木块A在整个过程中的最小速度值，应当是当木块A的速度首先减小到与木板C的速度刚好相等时的木块A的速度值。具体求解可采用以下几种方法。

方法一：用动量守恒定律求解

当木块A的速度首先减小到与木板C的速度刚好相等时，A的速度最小。设最小速度为v′，则B的速度为v0＋v′，由动量守恒定律有

mv0＋2mv0＝mv′＋m（v′＋v0）＋3mv′，

【点评】利用整个系统动量守恒解决问题，仅仅考虑A、B、C的初始状态和A的速度最小时A、B、C的末状态，不涉及中间过程，体现动量守恒定律解题的简捷性。

方法二：用动量定理求解

设木块A在整个过程中的最小速度为v′，达到v′的时间为t，

对木块A：μmgt＝mv0－mv′①

对木板C：2μmgt＝3mv′②

【点评】此方法对A、C用了动量定理，仅考虑A、C的初始状态和A的速度最小时A、C的末状态，也没有涉及中间过程，同样简单明了。

方法三：用牛顿第二定律求解

设木块A在整个运动过程中的最小速度为v′，达到最小速度所用的时间为t，注意此时木板受到的摩擦力大小是2μmg，由牛顿第二定律可得

对木块A：由μmg＝ma1得a1＝μg。

当木块A与木板C速度相等时A的速度最小，故有v0－a1t＝a3t，即

【点评】运用牛顿第二定律解决问题，涉及受力分析，注重分析过程，明确A、C的运动情况，过程分析详细，这说明分析物理过程很重要。

方法四：用动能定理求解

设木块A在整个运动过程中的最小速度为v′，达到最小速度所用的时间为t，

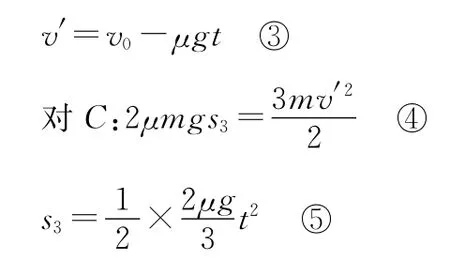
【点评】此法站在能量转化和运动学的角度处理问题，看似复杂但更有物理“味”，再次说明详细分析物理过程的重要性。

通过上述解法不难看出，解决这类问题时，整体把握用动量守恒定律和动量定理，局部把握用牛顿运动定律和动能定理（或功能关系）。在平时的学习或复习中，我们要注意对典型问题从多个角度进行思考，既发散了思维，又培养了能力，而且还构建了重点知识体系，何乐而不为呢？

（作者单位：河北省唐山市丰润区任各庄镇中学）