异形人行拱桥的舒适性分析

孙良凤，王炜龙，潘 磊

（1.浙江大学建筑设计院 市政交通分院,浙江 杭州310000；2.丽水市旧城改造有限责任公司,浙江 丽水 323000）

异形人行拱桥的舒适性分析

孙良凤1，王炜龙1，潘 磊2

（1.浙江大学建筑设计院 市政交通分院,浙江 杭州310000；2.丽水市旧城改造有限责任公司,浙江 丽水 323000）

针对异形人行拱桥自振频率不满足国内规范规定的不小于3 Hz这一问题,根据有限元模型分析,通过不同步伐荷载作用下的结构振动响应计算,分析在设计阶段其结构使用的舒适性,同时对已建成的异形人行拱桥进行动力荷载试验,验证动力响应计算方法在舒适度分析计算中的有效性。

频率；舒适性；人行桥

0 引 言

随着城市交通的快速发展,人行桥在解决城市交通的快速、通畅方面发挥着极其重要的作用。由于使用荷载小、设计自由度大,同时为了适应城市景观以及跨越的需要,近年来出现了一批刚度较小的大跨度柔性人行桥结构,使得振动问题在人行桥结构设计中变得尤为重要。

历史上,曾有多起由于振动问题引起的人行桥坍塌事故。其中较为著名的是2000年英国为迎接21世纪在泰晤士河建造了伦敦千禧桥[1],开通当日约有10万人同时涌入桥面,结果造成大幅振动和行人恐慌,最终该桥不得不临时关闭,耗巨资安装了粘滞阻尼器和质量调谐阻尼器后才重新开放。

这些事故的发生主要是设计时对人群荷载作用下的结构动力响应估计不足所致。目前,国内外对人行桥的振动舒适性验算主要有两种方法:一是采用结构的自振频率,如我国《城市人行天桥与人行地道技术规范》(CJJ 69—95)[2]规定结构的竖向自振频率不小于3.0 Hz；二是采用结构的振动响应,如德国EN03等标准[3-5]是根据步伐荷载作用下的振动响应来验算桥梁的舒适性。与前者相比,后者考虑了步行荷载和结构的动力特性,通用性强,已经成为研究人行桥舒适性问题的主要方法[6]。

本文针对不满足规范规定的自振频率不小于3.0 Hz的人行桥,通过不同步伐荷载作用下的结构振动响应计算,分析在设计阶段探索结构的使用舒适性。同时对一座跨度为105 m的异形人行拱桥进行动力荷载试验,以验证动力响应计算方法在舒适度分析计算中的有效性。

1 工程概况

一干河桥位于江苏省张家港市锦丰镇。跨越一干河的人行桥结构为全钢下承式异形拱桥。图1为桥梁的平面图、侧面图、立面图及钢梁横断面图。桥梁跨径布置为（12.5+105+12.5）m。桥面为曲线弧形结构,钢梁采用单箱双室截面；钢拱肋侧倾75。,在其自身平面内为二次抛物线,矢高为26.25 m,矢跨比为1/4,采用矩形单箱单室变截面,截面宽度由拱脚的3.5 m变至拱顶的2.0 m,截面高度由拱脚的2.0 m变至拱顶的1.5 m。

图1 人行桥结构布置图（单位:m）

由于该桥拱肋在面外的受力状态近似于悬臂结构,结构刚度较小,经midas软件计算得到的理论频率仅为0.94 Hz,不能满足规范规定的不小于3.0 Hz设计要求。

鉴于该桥结构形式已经超过了传统人行桥梁的概念,用规范不小于3.0 Hz的简单方法来验证桥梁的舒适性要求存在不少弊端,容易造成结构设计浪费的现象。因此进行相关的专题研究,通过不同步伐荷载作用下的结构振动响应计算结果,在设计阶段探索结构的使用舒适性,以及进行建成后的实测试验很有必要。

2 计算模型和工况

2.1 模型

为了进行桥梁振动的理论分析,建立了三维有限元分析模型。拱肋、桥面结构采用空间梁单元,吊杆采用桁架单元。

图2为有限元计算模型,顺桥向为Z轴,竖向为Y轴（向下为正）,水平横向为X轴。

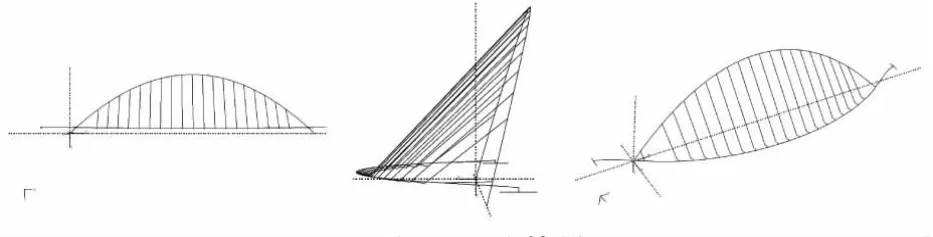
图2 有限元计算模型

2.2 工况

通过计算,得到前5阶结构自振频率。此后的频率超过3.0 Hz,认为步行频率已经避开,发生不舒适振动的可能性非常小,不在本文考虑之列。

根据桥梁的实际使用情况,并根据计算得到的自振频率（见表1）,通过走行、跑行工况的计算来分析桥梁的舒适性。

表1 走行和跑性工况人群密度与自振频率

2.3 计算方法以及舒适性指标

桥梁振动计算采用移动步伐荷载下的结构振动时程分析,其运动方程为:

式中:M为结构的质量矩阵；K为结构刚度矩阵；C为结构阻尼矩阵；分别为结构加速度、速度和位移响应；F（x,t）为与步伐作用对应的荷载向量。

舒适性等级与对应的振动加速度指标见表2。

表2 舒适性等级与振动加速度

图3为根据随机概率方法计算结构振动舒适性的计算框图。在可能发生人桥共振频率的1.5～3.0 Hz范围内,对每一个可能发生共振的自振频率作为步伐频率,根据随机人群结构振动响应分析结果分布特性,获得不同舒适性等级的桥梁舒适度评价结果。

图3 人行桥舒适性评估流程图

3 计算结果

3.1 步行工况

每种工况均计算了50组随机数据,取人群密度为0.3、0.6、0.9人/m2这3种状态。

图4～图6为步行频率范围内的前3个共振频率计算结果,这里分别给出跨中的最大速度和加速度。按表2进行分类,结果如表3所示。由表3可见,没有出现不可忍受的工况,个别工况为不舒适,大部分工况为很舒适或者中度舒适。

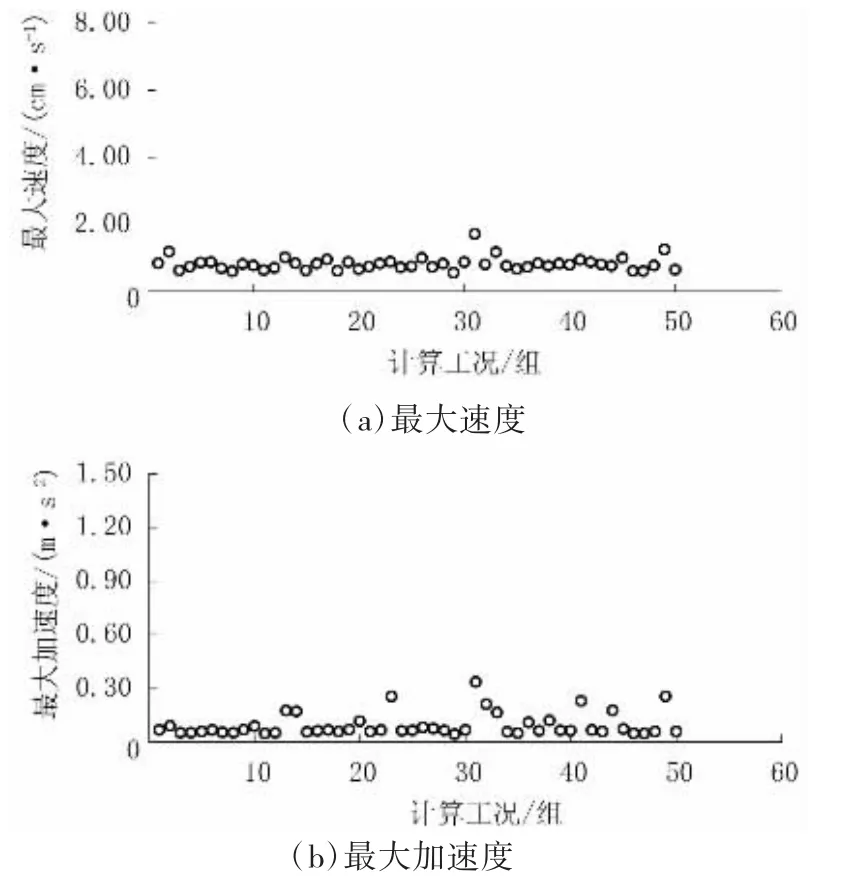
图4 按第一自振频率（0.3人/m2,f1）走行时的计算结果

图5 按第二自振频率（0.6人/m2,f2）走行时的计算结果

图6 按第三自振频率（0.9人/m2,f3）走行时的计算结果

表3 步行方式的舒适性分析结果

3.2 跑行工况

跑行每种工况也计算了50组随机数据,取人群密度为0.3、0.6、0.9人/m23种状态。在通常桥梁中,实际上当人群密度超过0.6人/m2时就很难跑行,这里作为一个工况仍进行了计算。

这里分别给出跨中的最大速度和加速度。按表2进行分类,结果如表4所示。由表4可见,个别工况发生不舒适,中度舒适和很舒适占主要比例,没有出现不可忍受的结果。

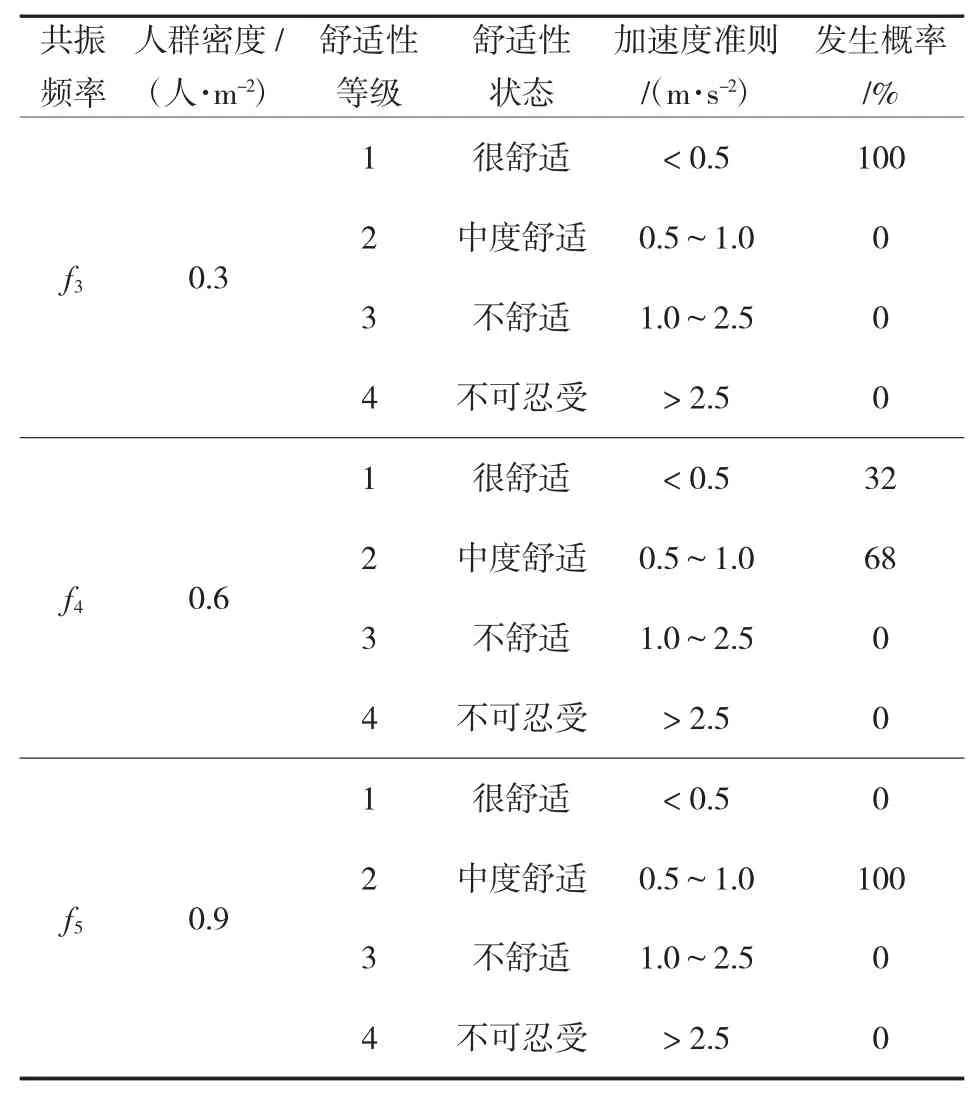
表4 跑行方式的舒适性分析结果

4 振动试验与计算结果对比分析

为了得到结构自振特性以及行人激励下的结构动力特性,对人行桥进行动力荷载试验。通过自然环境激励下的脉动试验及自由衰减响应时程得到结构各阶自振频率、振动模态及阻尼比；将计算得到的结构振动频率、振型与脉动测试结果进行对比,从而验证有限元模型的可靠性。

人行桥动载试验包括自然环境激励下的结构脉动试验以及行人特定行走工况条件下的强迫振动试验,见图7。在1/4跨、1/2跨、3/4跨处分别布置2个竖向拾振器,如图8所示,其中,Vo-1/4, Vo-1/2,Vo-3/4分别表示1/4跨、1/2跨、3/4跨中外侧竖向拾振器,Vi-1/4,Vi-1/2,Vi-3/4分别表示1/4跨、1/2跨、3/4跨中内侧竖向拾振器。测试与数据采集装置采用由中国地震局工程力学研究所研制的941B高灵敏低频传感器,仪器的采样频率设为200 Hz。

图7 动载试验现场示意图

图8 动载试验测点布置图

运用FFT快速傅里叶频谱分析法及ERA特征系统实现算法对结构的振动频率、振动模态以及各阶模态阻尼比进行振动参数识别。

Vi-1/4测点的FFT分析结果中较为明显的卓越频率为1.06、1.72、2.95 Hz,Vo-1/4测点较为明显的卓越频率为1.06、1.72、2.34、2.95 Hz。由于第三阶振型为扭转一阶对称,因此第三阶振动频率在外测点振动中要比在内测点振动中更为明显；由于第二阶振型为反对称竖向振动,因此Vi-1/2测点的FFT分析结果中较为明显的卓越频率仅为1.06、2.95 Hz,Vo-1/2测点的卓越频率为 1.06、2.34、2.95 Hz。

表5列出了结构前二阶有限元计算结果与上节分析得到的实测振动参数对比。由表5可见,理论结果与实测结果最大差异度小于0.5%,说明该计算模型能够真实反映结构的动力特性。

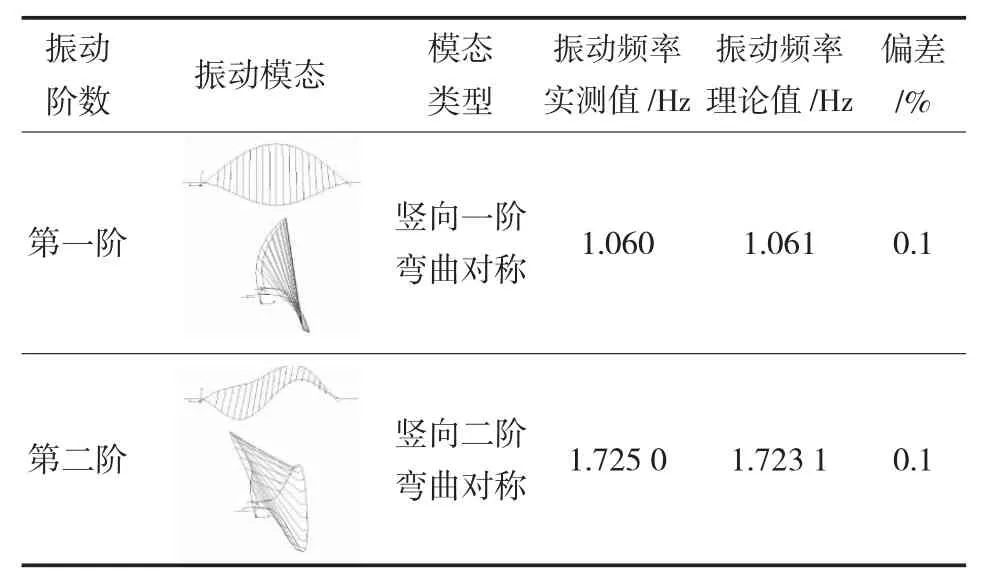
表5 人行桥结构振动特性对比

6 结语

（1）一干河桥除了个别工况可能会发生不太舒适的振动,总体上推断桥梁在使用期间不会因振动带来舒适性问题。

（2）有限元计算模型能够精确模拟人行桥结构的自振特性；同时理论计算结果与相同工况下的行人动载实测响应吻合度较高,说明本研究采用的人致振动响应计算方法具有较高精度。

[1]DALLARD P,FITZPATRICK A J,FLINT A,et al.The London millennium footbridge [J].Structural Engineer,2001,79(22): 17-21.

[2]中华人民共和国建设部.CJJ 69—95,城市人行天桥与人行地道技术规范[S].北京:中国建筑工业出版社,1996.

[3]HIVOSS(Human induced vibration of steel structure).EN 03—2007,Design of footbridges[S].Germany:2008.

[4]STETRA.Technical guide footbridges-Assessment of vibrational behavior of footbridges under pedestrian loading[S].Paris:Technical Guide,2006.

[5]British Standards Association.BS 5400,Steel,concreteand composite bridge-Part 2:Specification for loads[S].London:British Standards Association,1978.

[6]ZIVANOVIC S,PAVIC A,REYNOLDS P.Vibration serviceability of footbridges under human-induced excitation:A literature review [J].Journal of Sound and Vibration,2005,279(1):1-74.

U491.5

A

1009-7716（2017）07-0077-04

10.16799/j.cnki.csdqyfh.2017.07.023

2017-03-03

孙良凤(1985-),女,浙江宁波人,硕士,从事桥梁设计工作。