基于等效弹性模量的微裂纹-超声波非线性作用多阶段模型∗

杨斌 魏烁 史开元

(北京科技大学,国家材料服役安全科学中心,北京 100083)

基于等效弹性模量的微裂纹-超声波非线性作用多阶段模型∗

杨斌†魏烁 史开元

(北京科技大学,国家材料服役安全科学中心,北京 100083)

(2017年1月3日收到;2017年5月5日收到修改稿)

提出了一种基于等效弹性模量的微裂纹-超声波非线性作用多阶段模型.该模型将微裂纹微观层面的界面几何特征和宏观层面的界面相对运动统一为介观单元弹性模量的变化,利用等效弹性模量表征损伤区域的“应力-应变”,然后利用分段函数来描述微裂纹-超声波非线性相互作用,最后通过有限元仿真对波动方程进行求解,验证了模型的有效性,获得了超声波在经过微裂纹后传播的非线性波动规律.仿真结果表明本文提出的模型相比于双线性刚度模型、接触面模型,能更好地体现一个谐波周期内超声波经过微裂纹损伤区域时波形会发生畸变.同时,仿真实验还分析了裂纹倾角、裂纹长度和超声波激励幅值对超声波经过微裂纹后产生的二次和三次谐波的幅值的影响.最后,对比分析了该模型的仿真计算结果与实验测试结果,表明本文提出的多阶段模型与实验测试均能较好地体现微裂纹-超声波非线性作用产生的二次谐波信号,且结果基本一致,验证了模型的有效性.该模型为开展超声波非线性效应定量检测微裂纹提供了一种新的仿真手段.

微裂纹,超声波,等效弹性模量,多阶段

1 引 言

金属材料内部微裂纹的萌生和扩展是构件发生断裂的重要原因,而且微裂纹的大小和取向对构件断裂性质有重要影响,所以微裂纹的早期检测对于保障构件的服役安全具有重要意义[1-3].研究表明,超声波与材料损伤的非线性作用会明显增加高次谐波的幅值,是检测材料的早期损伤和微裂纹的有效手段[4-6].因此,研究人员提出了许多模型来对裂纹-超声波非线性作用进行解释.Friswell和Penny[7]提出双线性刚度模型,并使用数值模拟的方法验证了模型的有效性.Solove等[8]基于双线性刚度模型揭示了当超声波的应变幅值大于裂纹面的初始应变,可以将裂纹“打开”,产生非线性效应.双线性刚度模型在宏观层面上解释了裂纹面的相对运动对超声波的非线性调制作用,但忽略了裂纹面的微观几何特征,无法解释当超声波应变幅值小于阈值时产生的高次谐波现象.G reenwood和W illiamson[9]在Hertz理论[10]的基础上,引入接触面粗糙峰高度的概率分布,建立了接触面模型.Nazarov和Sutin[11]基于粗糙接触面模型验证了超声波作用于“闭合”粗糙界面时会产生高次谐波.南京大学声学研究所肖奇等[12]研究了不同粗糙峰高度的概率分布模型下超声波与接触面的非线性作用.接触面模型探索在微观层面上解释粗糙界面与超声波的非线性作用,但是没有考虑超声波与宏观“张开”的粗糙界面的非线性相互作用.

由于高次谐波的产生原因一方面是宏观层面上超声波与裂纹面开合的非线性作用,另一方面是微观层面上相互接触的粗糙界面与超声波的非线性作用.因此,本文旨在结合宏微观层面上超声波与微裂纹非线性作用的特性,完整地描述一个谐波周期内微裂纹与超声波的非线性作用,提出了基于等效弹性模量的微裂纹-超声波非线性作用多阶段模型.该模型将微裂纹粗糙界面的几何特征(粗糙峰高度峰)和宏观层面裂纹面的相对运动统一为介观单元弹性模量的变化,然后利用分段函数描述了在一个超声波谐波周期内连续介质损伤区域“应力-应变”的变化.仿真实验表明该模型可以很好地区分微裂纹在“开”,“闭”阶段的超声非线性效应,并可以开展微裂纹的尺寸、取向、粗糙界面特征的定量分析.

2 理论模型

假设在连续固体介质的一定区域内存在一条细长的裂纹,将裂纹附近的区域称为损伤区域(如图1(a)).根据Brown-Scholz模型[13],将两粗糙界面等效为裂纹粗糙面和裂纹平面,并假设一个参考平面来描述裂纹粗糙面和裂纹平面的相对运动.裂纹粗糙面相对参考平面保持不动,裂纹平面随着超声波的激励相对参考平面上下振动.本文假设两个位置为裂纹平面运动的参考点,位置一为裂纹完全张开的临界点,位置二为裂纹完全闭合的临界点,即当裂纹平面运动到位置一上方或者位置二下方时,裂纹完全张开或闭合.假设裂纹在位置一时应变为零,在位置二时应变为εn(＜0).考虑裂纹尖端存在塑性区,裂纹平面会在塑性作用下运动到位置一下方,并产生初始应变ε0(＜0),其对应的裂纹平面与参考平面之间的初始距离d0.同时,假设dm和dn为裂纹平面在位置一和位置二时与参考平面的距离(如图1(b)).

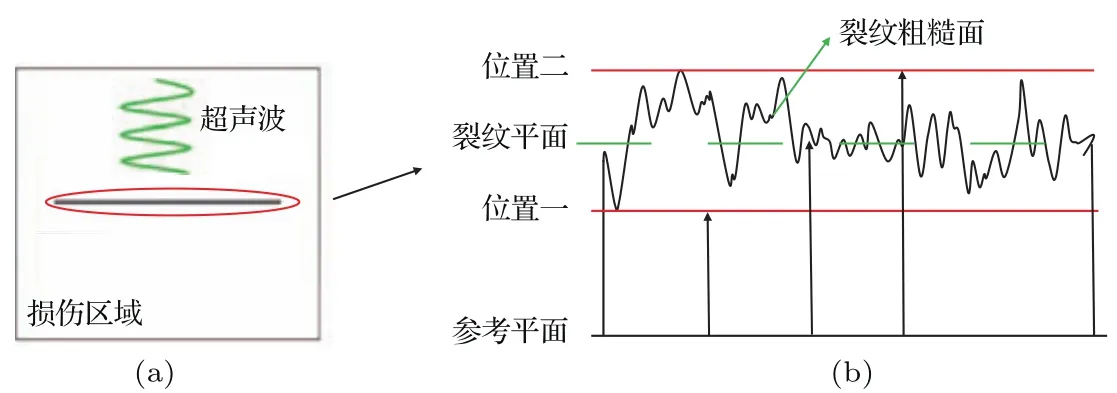
图1 (网刊彩色)裂纹粗糙面和裂纹平面的相对运动模型 (a)含裂纹的损伤区域;(b)相对运动模型Fig.1.(color online)Relative m otion model of crack rough surface and crack p lane:(a)Crack dam age zone;(b)relative m otion model.

假设一列纵波经过损伤区域,超声波的激励载荷ε(t)=εmaxcosωt,εmax表示入射声波引起的应变幅值,ω是角频率,超声波对裂纹张开闭合的作用如下：

当ε(t)+ε0＞0,裂纹平面与参考面之间的距离d＞dm,裂纹完全张开;

当εn＜ ε(t)+ε0＜ 0,裂纹平面与参考面之间的距离dn＜ d＜ dm裂纹面之间的距离dn＜d＜dm,裂纹非完全闭合;

当ε(t)+ε0＜εn,裂纹平面与参考面之间的距离d＜dn,裂纹完全闭合.

由于损伤区域存在裂纹,力学性能会发生变化,在超声波周期性载荷的作用下,裂纹会以相同的周期张开闭合,导致损伤区域的“应力-应变”关系也会以相同的周期变化.因此,在一个谐波周期的不同阶段难以用一个关系模型描述损伤区域的“应力-应变”关系.弹性模量是表征材料应力应变关系的物理量,本文通过使用“等效弹性模量”来描述一个谐波周期内损伤区域在不同阶段的“应力-应变”关系,并用分段函数描述了裂纹平面运动的三个阶段：

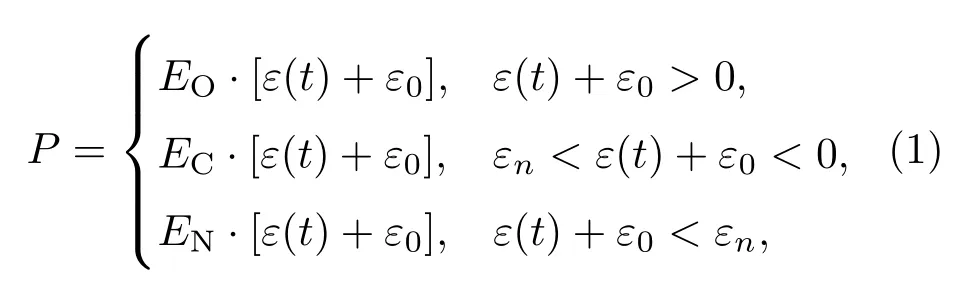
其中P代表损伤区域所受的应力,EO表示裂纹面完张开时损伤区域的弹性模量,EC表示裂纹面非完全闭合时损伤区域的弹性模量,EN表示裂纹面完全闭合时损伤区域的弹性模量.EO,EC,EN与裂纹尺寸、裂纹面粗糙度、裂纹面初始应变有关,并且假设E表示材料没有损伤时的弹性模量.

2.1 裂纹完全张开阶段的等效弹性模量E O

当一列纵波经过裂纹时,超声波周期性的拉伸和压缩载荷作用会使裂纹出现“呼吸效应”,即裂纹面将产生不断张开闭合的现象,如图2所示.

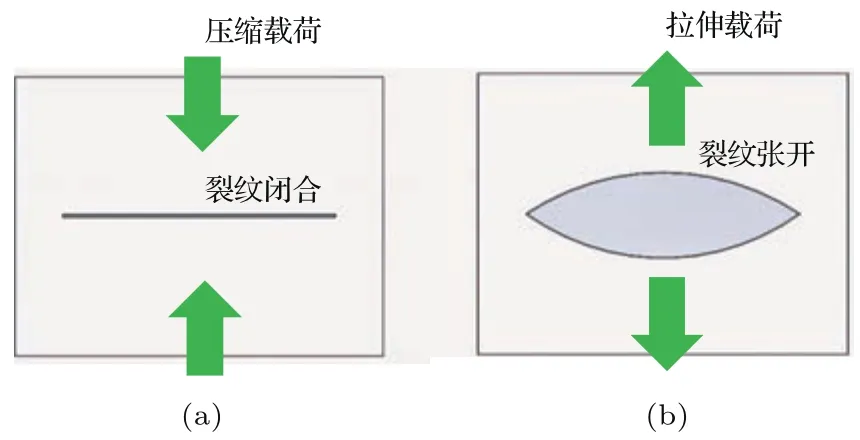
图2 裂纹在超声波拉压载荷下的呼吸效应 (a)裂纹被压缩闭合;(b)裂纹被拉伸张开Fig.2.Crack breathing effect under the tension and com p ression load of u ltrasonic:(a)Crack closing under the com p ressive load ing;(b)crack openning under the tension load ing.

在裂纹的完全张开阶段,当ε(t)+ε0＞0,本文采用有效介质方法对含有微小裂纹的损伤区域等效弹性模量进行求解,其核心思想是当裂纹承受外加应力,其周围有效介质的弹性模量由稀疏分布方法确定,具体计算公式如下[14]：

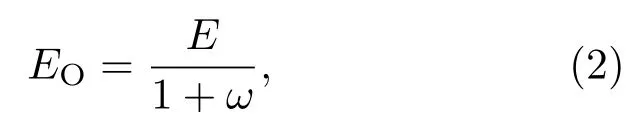
其中ω表示裂纹密度函数[14],

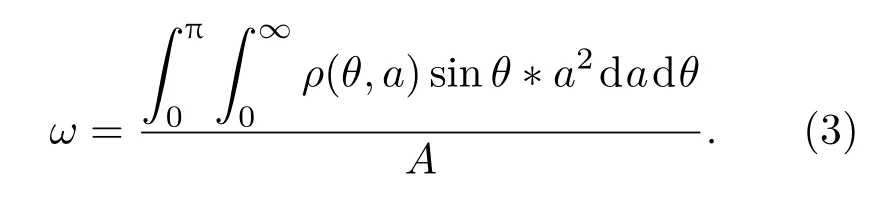
ρ(θ,a)是裂纹长度和裂纹倾角的分布密度函数,a为裂纹长度一半,θ为裂纹面法向与外加应力方向夹角,A为损伤区域面积.

对于含有单裂纹的损伤区域,本文通过对裂纹密度函数化简求得含有单裂纹的损伤区域在裂纹张开阶段的等效弹性模量EO为

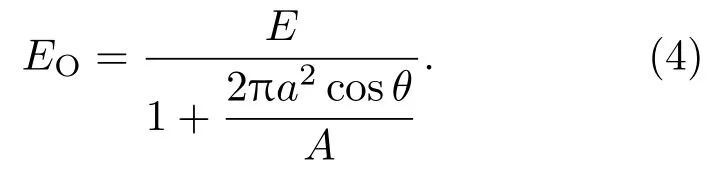
2.2 裂纹非完全闭合阶段的等效弹性模量E C

在裂纹的非完全闭合阶段,当εn＜ε(t)+ε0＜0,损伤区域的总应变εTOT由两部分组成,分别是损伤区域连续介质的弹性应变εE和裂纹产生的非线性弹性应变εC,如下式：

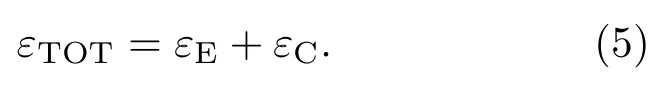
因此,通过引入裂纹所受应力σC和损伤区域的连续介质所受应力σE,则损伤区域的等效弹性模量EC的倒数由下式求得：

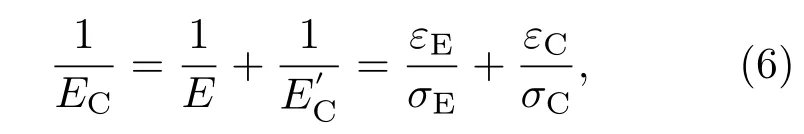
本文利用概率函数描述裂纹表面粗糙峰高度分布,建立裂纹粗糙表面所受应力与裂纹面之间距离的关系,具体计算公式如下[12]：

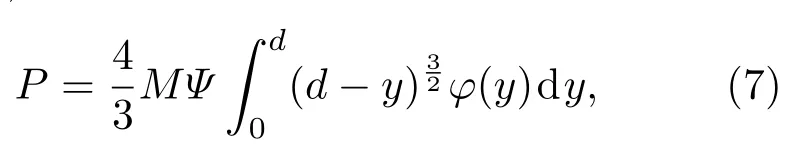
P为裂纹面所受正应力,M为裂纹面的粗糙参数, d为裂纹平面与参考面之间相对距离.φ(y)表示裂纹粗糙峰高度分布,本文采用高斯分布来描述固体表面的粗糙峰分布：

Ψ是对剪切力的存在而增加的几何校正因式,和裂纹面的倾斜角度θ有关.根据Hertz接触理论分别计算裂纹面的正应力FN和切向应力Fτ(忽略了裂纹表面的滑动),得到了几何校正因式Ψ：

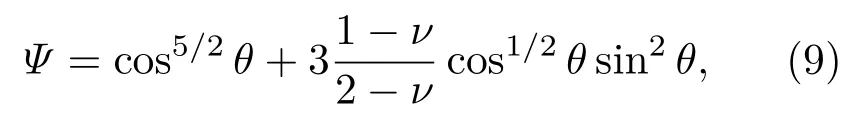
其中ν表示无损材料的泊松比.假设裂纹的宽度非常小,即裂纹面之间的位移极小,则裂纹面应变有如下的定义：

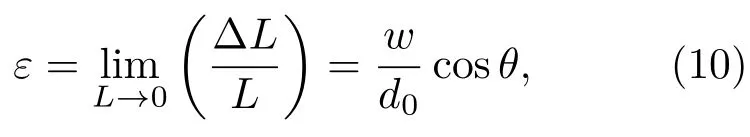
w为加载力方向上的位移,d0为裂纹参考面的距离,θ为裂纹面法向与力的夹角.接触应力通过对应变求导,得出损伤区域在裂纹面接触时弹性模量的变化规律：

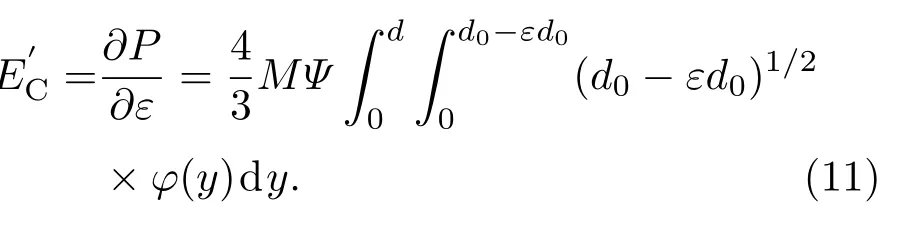
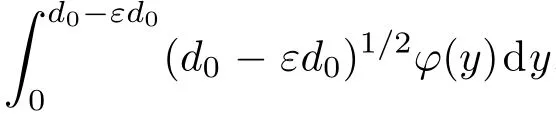
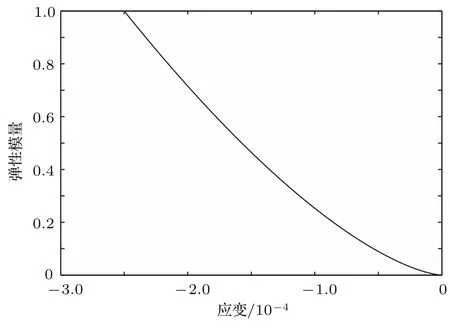
图3 损伤区域在裂纹面非完全闭合时的等效弹性模量ECFig.3.The equivalent elasticm odu lu EC of the damage zone as the crack surface is not com p letely closed.

2.3 裂纹完全闭合阶段等效弹性模量E N

当裂纹完全闭合时,ε(t)+ε0＜εn,裂纹表面的所有凸峰和凹谷已经完全接触,此时损伤区域的等效弹性模量为无损材料的弹性模量,

3 仿真实验与结果分析

3.1 仿真模型的建立

本文使用有限元方法对提出的三阶段裂纹-超声波的非线性作用模型进行仿真模拟,一方面验证模型的正确性,另一方面通过本模型定性分析裂纹参数对超声波非线性作用的影响.仿真实验中使用铜作为平板材料,其密度ρ=8960 kg/m3,声速c=4600 m/s,平板尺寸为20 mm×20 mm×20 mm.平板右端固定,设立两个数据采集点A和B,采集X方向的超声波信号,A点采集到的为未经过损伤区域的超声波信号, B点采集到的为经过损伤区域的超声波信号(如图4).

图4 有限元仿真建模Fig.4.Finite elem ent simu lation modeling.

在平板中间建立长度为1 mm的竖直裂纹,传统裂纹建模方法是通过模拟裂纹的几何形状和接口,并定义适当的接触条件,但由于裂纹表面形貌复杂,所以需要将裂纹区域离散成尺寸非常小的单元体,这在本质上容易造成单元的失真.本文通过使用非线性损伤单元替换裂纹及其周围的损伤区域,避免了传统裂纹建模的弊端,非线性损伤单元的“应力-应变”关系采用本文建立的三阶段模型描述,具体仿真计算步骤如图5所示.

图5 仿真流程图Fig.5.Sim u lation fl ow chart.

3.2 基于多阶段模型的裂纹-超声波非线性作用

仿真模拟过程中,在平板左端施加水平向右、周期2MHz、振幅4MPa的正弦载荷.

将本文提出的模型代入波动方程,并通过有限元模拟计算,结果如图6所示.图6(a)是A点和B点接收到的超声波时域信号,可以看出超声波在B点波形发生了严重畸变;图6(b)是经过傅里叶转换后的频域信号,对比发现B点的超声波频域信号产生了明显的二次谐波和少量的三次谐波.仿真结果表明本文提出的模型可很好地描述超声波与裂纹的非线性作用,验证了模型的正确性.

3.3 一个谐波周期内裂纹-超声波非线性相互作用

对比本文提出的多阶段模型、双线性刚度模型、接触面模型,计算一个谐波周期内三种模型对超声波波形畸变的影响.仿真实验采用频率为250 kHz、幅值为4 MPa的超声波,裂纹长度为1 mm,裂纹倾角为0°,非线性损伤单元的应力-应变关系分别由本文提出的多阶段模型、双线性刚度模型、接触面模型计算,其余参数与3.1节中参数保持一致,计算结果如图7所示.本文引入波形畸变因子K来描述波形发生畸变的强度,畸变越强越利于后期信号分析与处理,畸变因子K的计算方法为

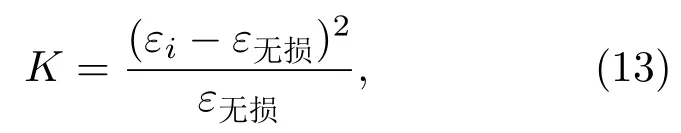
式中εi分别为多阶段模型、双线性刚度模型、接触面模型下超声波非线性作用引发的材料应变幅值.

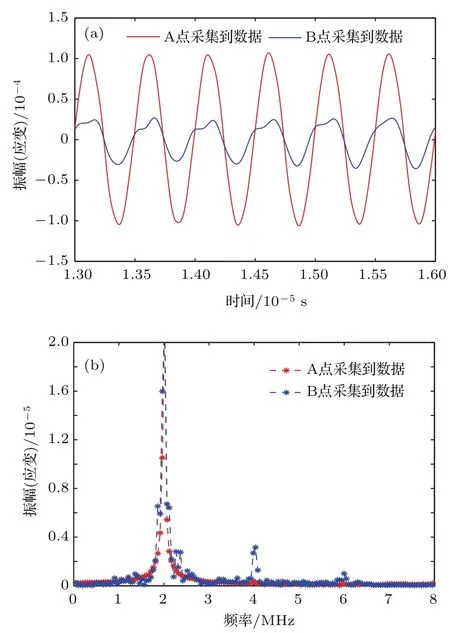
图6 (网刊彩色)超声波经过裂纹前后的信号对比 (a)时域信号;(b)频域信号Fig.6.(color online)Com parison of signals before and after u ltrasonic wave passing th rough crack:(a)Time dom ain signal;(b)frequency dom ain signal.

图7是一个谐波周期内超声波经过微裂纹后的波形图.采用接触面模型计算时,超声波的波形发生畸变,畸变因子K 值为1.30×10-2;采用双线性刚度模型计算时,超声波的波形发生畸变,畸变因子K值为1.32×10-2;采用本文提出的三阶段模型,在超声波拉伸和压缩载荷作用下,张开和闭合阶段都发生明显畸变,畸变因子K值为2.12×10-2.仿真结果表明本文提出的多阶段模型相比于双线性刚度模型和接触面模型,K值最大,能更好地体现超声波经过损伤区域时的非线性相互作用.

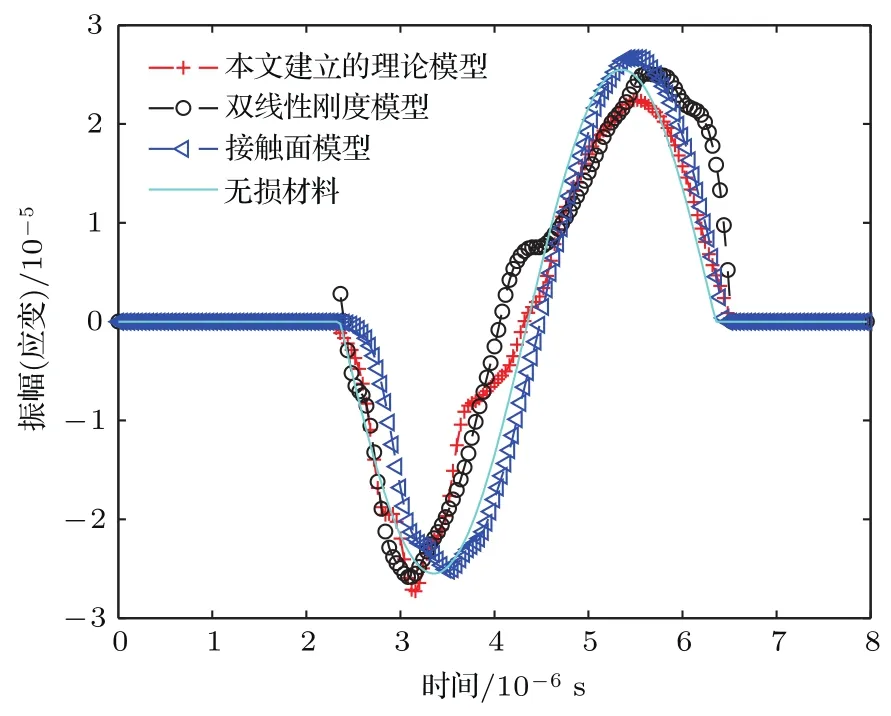
图7 (网刊彩色)不同模型的超声波波形畸变对比Fig.7.(color on line)Com parison of u ltrasonic waveform d istortion of d iff erent models.

3.4 裂纹特征参数和超声波幅值对超声波二次谐波幅值的影响

基于本文提出的多阶段模型,进一步研究裂纹倾角、裂纹长度、超声波幅值对微裂纹-超声波非线性效应的影响,设计了3因素4水平的试验(如表1).超声波频率采用2MHz,材料和尺寸参数与3.1节仿真模拟一致.

表1 不同裂纹特征参数对比试验Tab le 1.Com parative test with different crack characteristic param eters.

3.4.1 裂纹倾角对微裂纹-超声波非线性效应的影响

仿真参数：超声波幅值为4 MPa,裂纹长度为1 mm,裂纹面的初始应变为-0.0001,分别设置不同的裂纹倾角进行对比实验,超声波经过微裂纹后的时域和频域信号如图8所示.

图9是在不同的裂纹倾角情况下,计算了超声波经过微裂纹后高次谐波幅值的变化规律.结果表明超声波的传播方向与裂纹面法线的夹角越大,高次谐波的幅值越小;从0°到60°,二次谐波的幅值减小了13%,从60°到90°二次谐波的幅值减小了82%.这是由于仿真采用纵波发射和接收,当裂纹倾角越小,裂纹面上产生的非线性应变分量就越大,损伤区域的弹性模量变化也就越大,超声波的非线性行为越明显.特别地,当裂纹倾角为90°时,裂纹面与纵波传播方向平行,二次谐波的幅值几乎为零,此时将无法检测到裂纹的存在.三次谐波幅值的变化也体现了相同的规律.

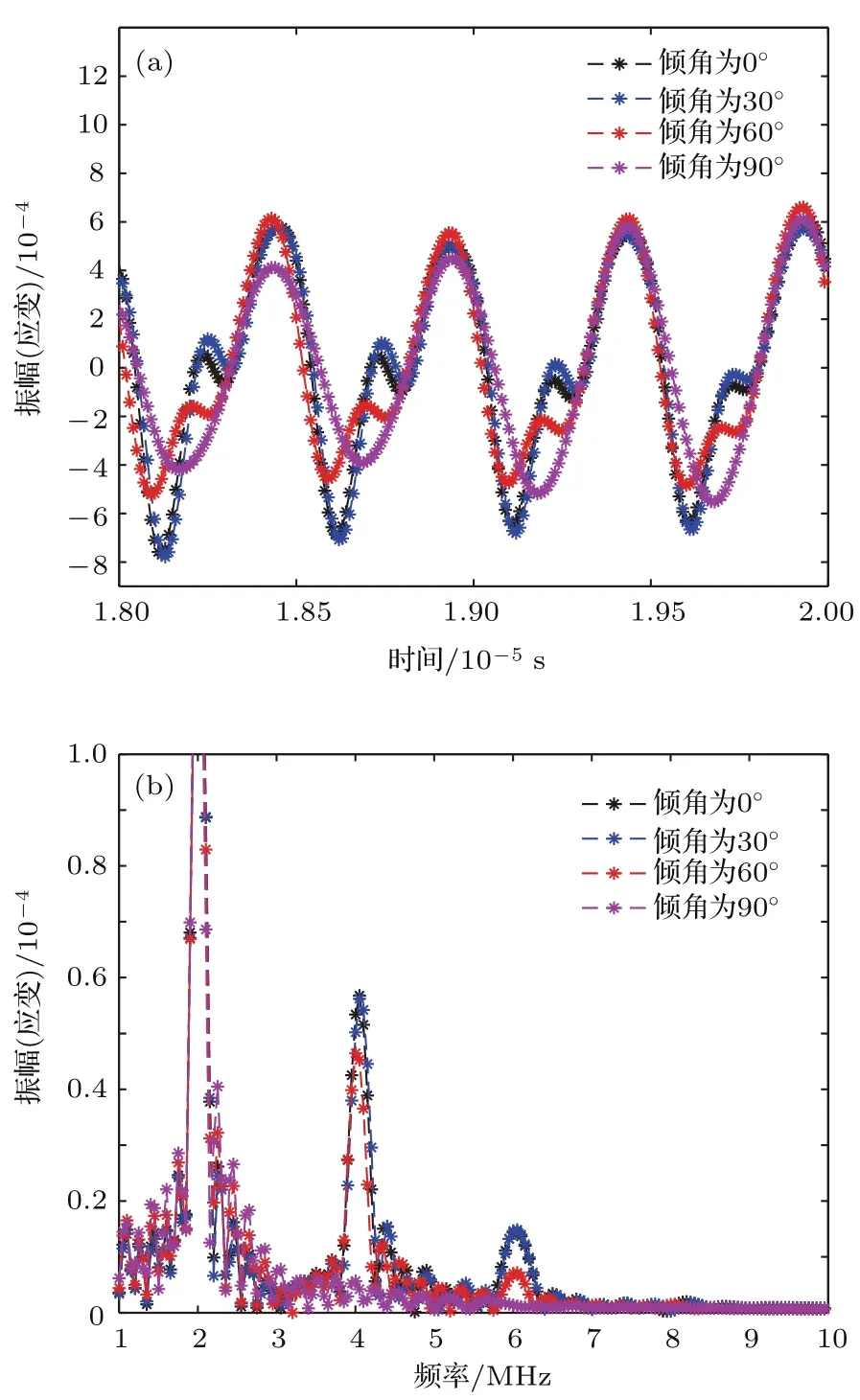
图8 (网刊彩色)不同裂纹倾角对超声波非线性效应的影响 (a)时域信号;(b)频域信号Fig.8.(color on line)The in fluence of different crack angle on u ltrasonic nonlinear effect:(a)Time dom ain signal;(b)frequency dom ain signal.

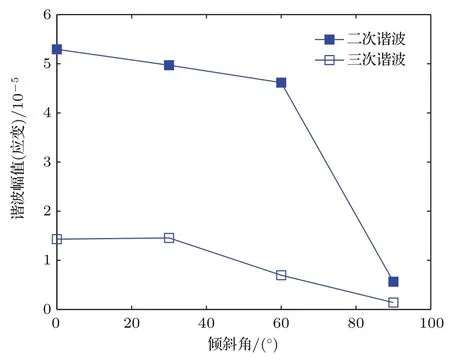
图9 裂纹倾斜角对超声波高次谐波幅值影响Fig.9.The in fluence of d iff erent crack angle on higher harm onic am p litudes of u ltrasonic.

3.4.2 超声波激励幅值对超声波非线性效应的影响

仿真参数：裂纹长度1mm,倾角为0°,裂纹面的初始应变为-0.0001,分别设置不同的超声波激励幅值进行对比实验,超声波经过微裂纹后的时域和频域信号如图10所示.

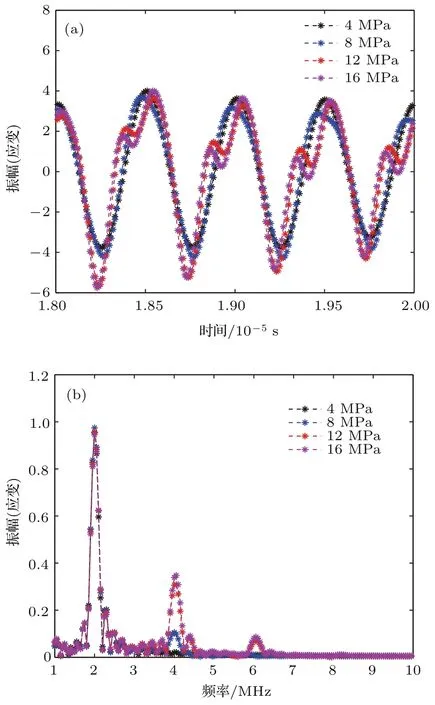
图10 (网刊彩色)不同超声波激励幅值对超声波非线性效应的影响 (a)时域信号;(b)频域信号Fig.10.(color online)The in fluence of different ultrasonic excitation amplitude on ultrasonic nonlinear effect:(a)Time dom ain signal;(b)frequency dom ain signal.

图11是在不同的超声波激励幅值下,计算了超声波经过微裂纹后高次谐波幅值的变化规律,结果表明高次谐波幅值随着超声波激励幅值的增加而增加.为了定量地比较激励幅值对超声波非线性效应的影响,将超声波的基波幅值进行了归一化处理.由图11可以看出,当超声波幅值从4 MPa增加到8 MPa时二次谐波的幅值增加了0.104;从8 MPa增加到12 MPa时二次谐波的幅值增加了0.2;从12 MPa增加到16 MPa时二次谐波的幅值增加了0.04,幅值增加先快后慢.其主要原因是：当超声波激励幅值低于8 MPa时,裂纹面始终闭合,二次谐波不明显,当大于阈值时,二次谐波幅值增加明显,但当激励幅值继续增加时,此时二次谐波的幅值不会继续增加.三次谐波幅值的变化也体现了相同的规律.

3.4.3 裂纹长度对超声波的非线性效应的影响

仿真参数：超声波激励幅值4 MPa,裂纹面的初始应变为-0.0001,分别设置不同的裂纹长度进行对比实验,超声波经过微裂纹后的时域和频域信号如图12所示.

图13是在不同的裂纹长度下,计算了超声波经过微裂纹后高次谐波幅值的变化规律.从图12的计算结果可以看出：随着裂纹长度不断增加,超声波非线性效应不断增强,当裂纹长度为0.4mm时,二次谐波幅值不太明显;当裂纹长度为0.8 mm时,已经可以明显观测到二次谐波的幅值,从而验证了采用超声波非线性效应检测微裂纹的可行性.从图13的计算结果可以看出：二次谐波和三次谐波幅值的增加与裂纹长度增加近似呈线性关系,依据此规律可以在实际测量中定量检测裂纹的长度.

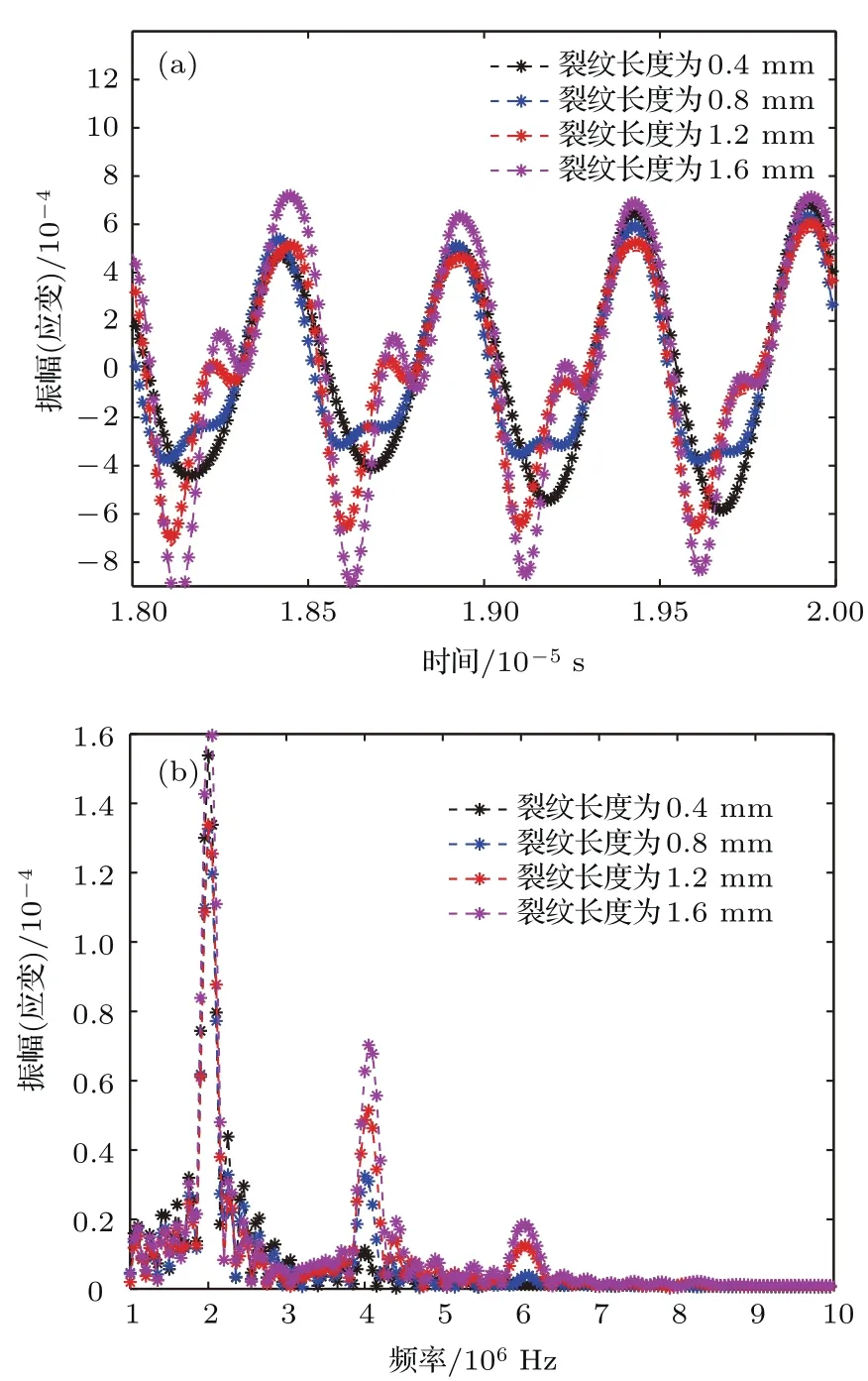
图12 (网刊彩色)不同裂纹长度对超声波非线性效应的影响 (a)时域信号;(b)频域信号Fig.12.(color on line)The in fluence of different crack length on ultrasonic nonlinear effect:(a)Time dom ain signal;(b)frequency domain signal.

图13 裂纹长度对超声波高次谐波幅值的影响Fig.13.The in fluence of different crack length on higher harmonic amplitudes of ultrasonic.

3.5 实验验证与分析

为了验证本文提出模型的有效性,进行实验测试,实验测试系统结构如图14所示.实验测试过程中,函数信号发生器(Tektronix AFG3022B)产生20周期频率为2.5 MHz、电压幅值为5 V正弦波信号;功率放大器(ENI2100L)放大和驱动超声换能器,功率放大增益为50 dB;发射换能器中心频率2.5 MHz,频率带宽为2.25-2.80 MHz;接收换能器中心频率5 MHz,频率带宽为4.55-5.60 MHz;数字示波器(Tektronix DPO2024)采样分析非线性超声信号.

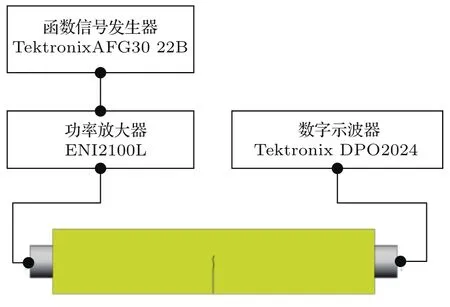
图14 实验系统结构图Fig.14.The structure diagram of the experim ental system.

实验采用黄铜H59作为实验材料,弹性模量为110 GPa,泊松比为0.33,试样尺寸为20 mm× 20 mm×100 mm.在试样中间使用线切割预制长7 mm、宽0.2mm的缺口,如图15所示.通过在三点弯曲试验机(Amsler HFP 5000)上加载频率为80 Hz、幅值为3.8 kN的循环载荷,预制出裂纹长度为3mm疲劳裂纹,如图16所示.

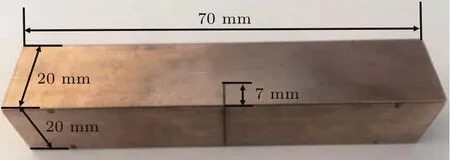
图15 试件尺寸Fig.15.D im ensions of specim en.

建立与试样相同的仿真几何模型,将试样的裂纹近似等效为20mm×20mm×20mm的损伤区域,依据(2),(6),(11),(12)式近似求得损伤区域的多阶段等效弹性模量变化,如图17所示.

对比分析实验测试和仿真计算所得到超声波信号,对信号进行傅里叶转换并进行归一化处理,得到的超声波频域信号如图18所示,可以看出实验测试和仿真计算超声波信号的频谱成分中均出现了5MHz的二次谐波分量,而且实验结果与仿真结果基本一致,从而验证了本文模型的有效性.

图16 裂纹扩展Fig.16.Crack p ropagation.

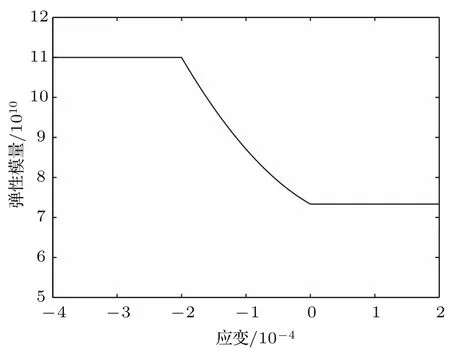
图17 损伤区域应变-弹性模量关系变化Fig.17.Relationship between strain and elasticm odu lus in the dam age area.

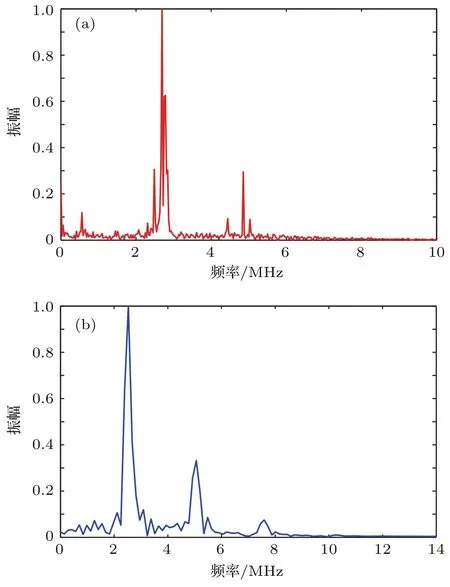
图18 实验与仿真结果对比分析 (a)归一化的实验测试频域信号;(b)归一化的仿真计算频域信号Fig.18.Com parative analysis of experim ental and simu lation resu lts:(a)Norm alized experim ental Frequency signal;(b)norm alized sim u lation frequency signal.

4 结 论

本文提出了一种基于等效弹性模量的微裂纹-超声波非线性作用多阶段模型,完整地描述了一个谐波周期内微裂纹-超声波的非线性相互作用,能够清晰地表征高次谐波是由于微裂纹粗糙界面的几何特征(粗糙峰高度分布规律)和宏观层面裂纹面的相对运动共同作用的结果.有限元仿真结果表明,本文提出的多阶段模型相比于双线性刚度模型、接触面模型能够更好地体现微裂纹-超声波的非线性相互作用.同时,基于本文提出多阶段模型,进一步探索了裂纹倾角、裂纹长度、超声波幅值对微裂纹-超声波非线性效应的影响.实验测试与仿真计算的结果对比分析验证了本文提出的多阶段模型的有效性.因此本文提出的基于等效弹性模量的微裂纹-超声波非线性作用多阶段模型,可以有效地探究裂纹的单个特征参数对超声波非线性效应的影响,为研究超声波非线性效应、定量检测微裂纹提供了新的仿真手段.

[1]Jhang K Y 2009 Int.J.Precis Eng.M an.10 123

[2]Chen Z J,Zhang S Y,Zheng K 2010 Acta Phys.Sin.59 4071(in Chinese)[陈赵江,张淑仪,郑凯 2010物理学报59 4071]

[3]W u M,Guo F,Li M,Han Y 2016 M ater.Sci.Forum. 849 603

[4]Broda D,Staszew skiW J,M artow icz A,Uh l T,Silberschm id t V V 2014 J.Sound.Vib.333 1097

[5]Lim H J,Song B,Park B,Sohn H 2015 NDT&E In t. 73 8

[6]M atlack K H,K im J Y,Jacobs L J,Qu J 2015 J.Nondestruct Eval.34 273

[7]Friswell M I,Penny J E T 2002 Struct Health M onit.1 139

[8]Solodov IY,K rohn N,Busse G 2002 U ltrasonics 40 621

[9]W illiam son J B P,G reenwood J A 1966 Proc.R.Soc. London A 19 295

[10]Baltazar A,Rokh lin S I,PecorariC 2002 J.M ech.Phys. So lids.50 1397

[11]Nazarov V E,Su tin A M 1998 J.Acoust.Soc.Am.102 3349

[12]X iao Q,W ang J,Guo X S,Zhang D 2013 Acta Phys. Sin.62 275(in Chinese)[肖齐,王珺,郭霞生,章东2013物理学报62 275]

[13]B rown S R,Scholz C H 1985 J.Geophys.Res.90 5531

[14]Cai M,Horii H 1992 M ech.M ater.13 217

(Received 3 January 2017;revised manuscript received 5 May 2017)

Modelling of multi-stage nonlinear interaction of micro-crack and ultrasonic based on equivalent elastic modulus∗

Yang Bin†Wei Shuo Shi Kai-Yuan

(University of Science and Technology Beijing,National Center for Materials Service Safety,Beijing 100083,China)

A multi-stagemodel of nonlinear interaction betweenmicro-crack and ultrasound based on equivalent elasticmodulus is p resented in this paper.In thismodel,the interface characteristics ofmicro-cracks at amicro-leveland the relative m otion at am acro-level are unified into an elasticm odu lus of them esoscopic elem ent.The equivalent elasticm odulus is used to characterize the“stress-strain”of the damage region.Then piecew ise function is used todescribe the nonlinear interaction between u ltrasound and micro-crack.Finally,the wave equation is solved by the finite elem ent simulation. In thism anner,the nonlinear interaction law between u ltrasound and micro-crack is obtained,and the validity of the model is verified.The simulation results also show that com pared with bilinear stiff ness model and contact surface model,the mu lti-stage model can well refl ect the distortion of the waveform in one period of ultrasonic wave passing through themicro-crack.In addition,the influences of the crack angle,the crack length and the input am p litude on the second harmonics generation and the third harmonics generation are analyzed.In the end,the com parison and analysis of the experim ental test and simulation calculations based on the p roposed mu lti-stage model show that the proposed multi-stagemodel and the experimental test can well refl ect the second harmonic signal p roduced by the nonlinear interaction ofmicro-crack and u ltrasound,and the second harmonic am p litudes of the experimental test are basically the sam e as the simulation calcu lations based on the proposed multi-stagemodel.Thus,the effectiveness of theproposed multi-stagemodel is verified.Themodel provides a new simulation method to quantitatively detect themicro-crack by ultrasonic nonlinear effect.

micro-crack,ultrasonic,equivalent elasticmodulus,multi-stage

PACS:43.25.+y,43.35.+d DO I:10.7498/aps.66.134301

∗国家自然科学基金(批准号:51575038,51471022)和中央高校基本科研业务费(批准号:TW 201710,FRF-BD-16-004A)资助的课题.

†通信作者.E-m ail:binyang@ustb.edu.cn

PACS:43.25.+y,43.35.+d DO I:10.7498/aps.66.134301

*Pro ject supported by the National Natu ral Science Foundation of China(G rant Nos.51575038,51471022)and the Fundam ental Research Funds for the Central Universities of M inistry of Education of China(Grant Nos.TW 201710,FRF-BD-16-004A).

†Corresponding author.E-m ail:binyang@ustb.edu.cn