基于足印探测的激光测高仪在轨标定∗

易洪 李松 马跃 黄科 周辉 史光远

(武汉大学电子信息学院,武汉 430072)

基于足印探测的激光测高仪在轨标定∗

易洪 李松†马跃 黄科 周辉 史光远

(武汉大学电子信息学院,武汉 430072)

(2017年1月8日收到;2017年5月4日收到修改稿)

高精度的地表目标三维观测结果需要卫星激光测高仪对其系统误差进行定期的在轨标定工作,这包含系统误差的估计和校正以及标定结果的精度检验,现有方式分别通过姿态机动法和足印探测法予以实现.然而,姿态机动方式不适用于我国的卫星平台,传统足印探测方式没有针对系统误差的估计模型,仅能用于标定结果的精度检验.本文推导了基于足印探测方式的激光指向角系统误差估计模型,使得足印探测法能完成包含在轨误差校正以及精度检验的工作闭环,同时对用于激光足印获取的地面能量探测器进行了改进设计.通过设计仿真实验对所推导的误差估计模型进行验证,并量化分析了探测器阵列激光入射角度、标定场地表粗糙度及探测器布设间距等因素对系统误差校正精度的影响.结果表明,若要实现1.8 m的水平定位精度(对应0.6 arcsec激光指向精度),探测器阵列间距达到20 m即可,探测器阵列面的入射角需高于3°,标定场地表粗糙度需小于10 cm.以上结论对我国未来发射GF-7号光学/激光立体测绘卫星具有重要参考价值.

星载激光测高仪,系统误差,在轨标定,能量探测器

1 引 言

星载激光测高仪是一种星对地的高精度激光测量设备,它可以根据发射激光脉冲的渡越时间(time of fl ight,TOF)得到测高仪与被测目标之间的距离值[1,2],结合高精度定姿系统测量的激光指向及卫星姿态信息可得激光测距向量,进一步结合高精度定位系统测量的卫星位置矢量,可得激光足印中心在指定坐标系下的定位向量[2,3],从而实现对被测目标高精度三维观测的目的.由于测量精度高,因此星载激光测高仪在多个科学领域具有广泛的应用前景,如海洋学、灾难预报、地形学、地球动力学等[4,5],然而测高仪足印中心三维坐标的定位精度受到系统误差的影响,其中主要系统误差为激光指向角误差及测距误差[6].测距误差直接影响高程精度;激光指向角误差主要影响足印定位的平面精度,对高程精度影响较小.假设地面斜率为一维分布,对于如ICESat(Ice,Cloud,and Land Elevation Satellite)卫星600 km 的轨道高度,1°综合入射角的条件下,30 arcsec的指向角误差将导致足印中心约87 m的平面偏差及1.5m高程方向偏差[7].

为了保证星载激光测高仪足印中心的定位精度,有必要对测高仪实施细致的在轨标定.首先,通过在轨校正对影响测高仪足印中心定位精度的系统误差进行解算;其次,通过在轨检定对系统误差的校正结果进行确认,从而有效剔除系统误差对足印中心定位精度的影响[8,9].ICESat卫星上搭载的激光测距仪GLAS(geoscience laser altimeter system)是目前惟一已运行具备波形记录功能的、对地球两极区域进行观测的激光测高仪,在其发射升空以后,美国国家航空航天局对其指向误差等指标进行了细致的在轨校正和在轨检定,其中在轨校正和在轨检定分别使用的是姿态机动法和足印探测法[7,10].姿态机动的在轨校正是通过卫星平台过境平静海面时进行姿态机动,对测距系统的测距观测值进行残差(测距模型距离解算值与测高系统距离实测值的差值)分析,达到校正指向角误差及测距误差的目的[7].该在轨校正法对卫星平台的要求较高,需要卫星平台具备稳定的姿态控制能力及精确的姿态测量能力.足印探测的在轨检定是通过在检定场布设能量探测器的方式俘获足印从而获得足印中心的“坐标真值”,将其与测高仪测得的足印中心坐标值进行比较,从而实现指向角误差在轨校正结果的在轨检定[10-12].

当前我国遥感测绘卫星发展迅猛,计划发射多颗搭载激光测高载荷的测绘遥感卫星[13].然而现有的在轨校正方法不适用于我国的大平台、三轴姿态稳定卫星平台,现有的在轨检定方法没有针对系统误差的在轨校正模型,其只能用于测高仪系统误差在轨校正结果的在轨检定.本文基于足印探测的在轨检定方法,推导了基于指向角残差的指向角系统误差在轨校正模型,使得足印探测的在轨检定法能够用于系统误差的在轨校正,避免了姿态机动在轨校正方法的需求,同时对用于足印探测的探测器进行了改进设计.基于推导的指向角系统误差在轨校正模型进行仿真实验设计,对校正模型进行评估,并分析多种因素对校正结果精度的影响,如激光在探测器阵列面的入射角、标定场地表粗糙度及探测器布设间距等因素.仿真分析结果表明,推导的指向角系统误差在轨校正模型能够有效反演指向角系统误差;增加激光在探测器阵列面的入射角及减小标定场地表粗糙度,都能有效提升推导的指向角系统误差在轨校正模型对系统误差的反演精度.此外,探①——模型对系统误差的反演精度在小范围内变化.将改进的探测器用于我国自主研制的首个对地观测试验性星载激光测高仪的在轨标定实验,卫星实验结果表明,资源三号02星上搭载的激光测高仪高程测量精度由标定前的6.3 m提高到了1.6 m.这对我国未来发射的星载激光测高仪实现业务化运行具有重要价值.

2 足印探测在轨标定

星载激光测高仪发射激光脉冲到达地表时足印中心的定位方程如(1)式所示,其本质是矢量的加法[2].

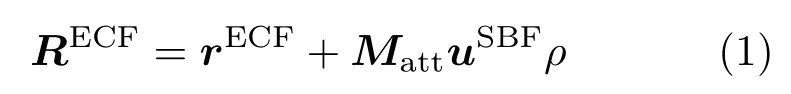
式中上标表示对应参量所在的参考坐标系,此处为地心惯性坐标系(earth centered inertial reference frame,ECF);ρ为根据渡越时间解算得到的激光测距值;u为激光指向测量系统测得的激光在卫星载体坐标系(spacecraft body fixed frame,SBF)下的指向单位向量;Matt为测高仪高精度定姿系统测得的卫星载体平台在ECF坐标系下的姿态矩阵;r为星上系统测得的激光出射点在ECF坐标系下的定位向量;R为足印中心定位向量[2].足印中心定位原理如图1所示.

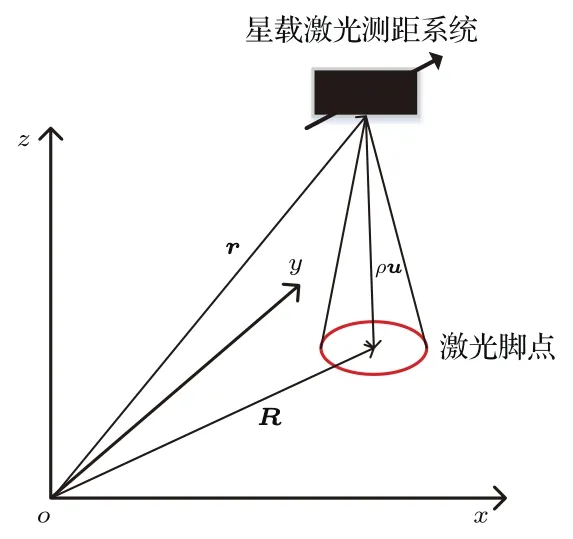
图1 激光测高仪足印定位Fig.1.Laser altimeter footp rint geolocation.

星载激光测高仪在轨运行时,由于震动和空间环境温度变化等因素的影响,使得测高仪激光指向的测量数据存在系统误差,影响测高仪足印中心的定位精度.为了确定足印中心定位精度受指向角误差的影响程度,有必要采用一种直接的检定方式获取激光脉冲到达地面时足印中心所在位置,将检定法得到的足印中心位置数据与测高仪定位方程解算得到的足印中心位置数据进行对比,即可达到检定星载激光测高仪定位精度进而检定激光指向角测量精度的目的.在平坦地面布设能量探测器的方式能根据被触发的探测器位置及探测器响应数据来提取激光脉冲到达地面时足印中心所在的位置数据,且探测器位置及响应数据的获得都不依赖于星上测量数据,因此称足印探测法为直接的检定方法[10-12].探测器俘获足印的原理如图2所示.检定区域布设的能量探测器的三维坐标由GPS(global positioning system)测量得到,结合被触发能量探测器的能量响应数据,就能对足印中心进行定位.

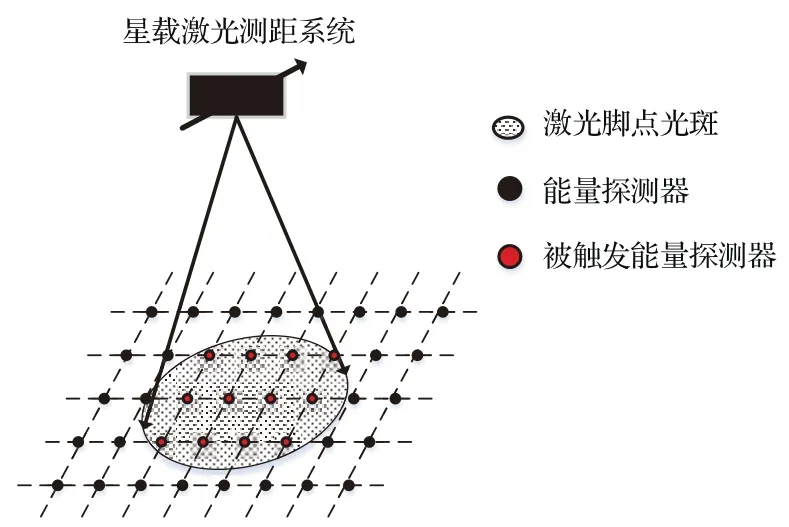
图2 (网刊彩色)能量探测器俘获激光光斑Fig.2.(color on line)Laser footp rint cap tu re by energy detector.

2.1 能量探测器的改进设计

针对GLAS的在轨检定,其设计的能量探测器为两个能级[12].由足印中心的定位算法可知,探测器的量化能级越多,探测器布设间距越密,对应的足印中心定位精度就越高,反之,探测器定位足印中心的精度就越低.基于足印中心的定位算法设计仿真实验,分析能量探测器能级数及布设间距对足印中心定位精度的影响.假定激光能量分布近似满足高斯分布,足印中心能量(I0)为1,足印半径(ω)为35m.固定探测器布设间距生成探测器阵列,随机生成1000个足印中心坐标((xf,yf))作为真值输入仿真实验,同时考虑到大气中的烟雾及灰尘等颗粒对大气透过率的影响,选定随机噪声因子(n)为0.3(一倍方差)[14,15],从而可确定每个探测器所处位置的能量,其计算公式为

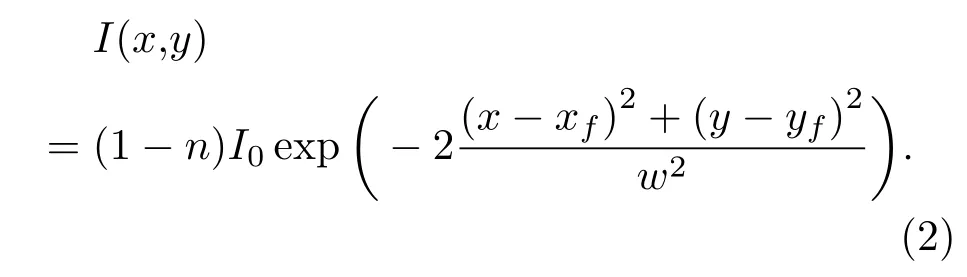
使用探测器确定的能量值对探测器的位置进行加权提取探测到的足印中心坐标,比较输入足印中心坐标真值与探测器定位的足印中心坐标之间的偏差,对偏差值进行统计得到其均值和标准差,可得探测器对足印中心的定位精度.改变探测器的能级数,则可得不同能级数条件下探测器对足印中心的定位精度.仿真结果如图3所示.

由图3可得,选定探测器布设间距后,当探测器能级数达到8级时,足印中心的定位精度随着能级数的增加不再有显著提升.综合考虑探测器的集成度及成本,在尽量提升探测器定位精度的前提下,将探测器的能级设定为8级.

2.2 指向角系统误差在轨标定模型

在足印探测法所选定的检定区域建立局部垂直局部水平参考坐标系(local vertical local horizontal frame,LVLH),由于卫星平台过境检定区域的时间很短(秒量级),此时可认为SBF坐标系与LVLH坐标系近似平行.在检定区域LVLH坐标系下,测高仪足印中心定位方程如(3)式.式中各项参数定义如(1)式,后文中如无特殊说明,描述测量值的参考坐标系均为LVLH坐标系.

通过坐标系的转换将足印探测定位的足印中心坐标转换到LVLH坐标系下.假设足印探测得到的足印中心位置向量为Rd,并以此为测高仪足印中心位置的“真值”,结合足印中心定位方程((3)式)即可解算得到激光测距矢量,计算公式为

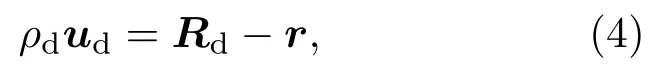
式中Rd为经过坐标系转换后探测器定位的足印中心位置向量;r为测高仪激光出射点的位置矢量;ρd为计算距离值;ud为逆向计算所得激光指向单位向量.将(4)式计算得到的激光指向单位向量与激光测高仪星上系统测量的激光指向单位向量进行点乘,可得激光指向角残差(pointing residual, PR),基于指向角残差建立指向角误差校正模型,即可对星上系统测量的激光指向向量方向余弦中的三个角度进行校正.

将激光测高仪星上系统测量的激光指向单位向量(u)用坐标表示,如(5)式,

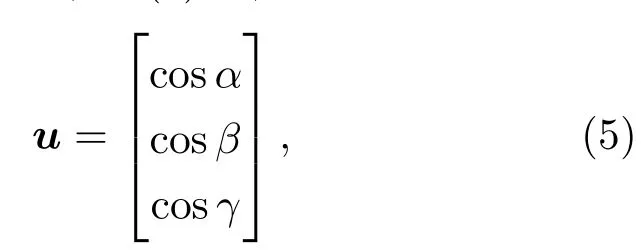
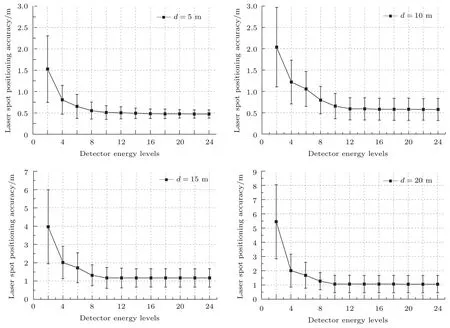
图3 不同能级数对应激光定位精度Fig.3.Footp rint geolocation accuracy under different energy levels.

式中cos(α),cos(β),cos(γ)为星载激光测高仪星上系统测得的激光指向单位向量的方向余弦,其中α, β,γ依次分别为激光指向单位向量与LVLH坐标系X,Y,Z轴的方向余弦角[2].同理可得通过足印探测计算得到的激光指向单位向量(ud)如(6)式,式中各项参数定义如(5)式.

假设激光指向单位向量方向余弦角中的系统误差依次为δα,δβ,δγ,随机误差依次为eα,eβ,eγ,则有

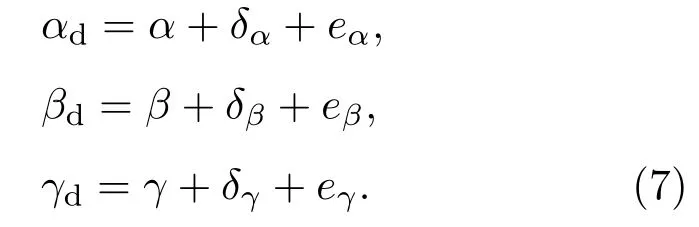
将(7)式代入(6)式,并将测量激光指向单位向量((5)式)和计算激光指向单位向量((6)式)点乘,可得观测方程为

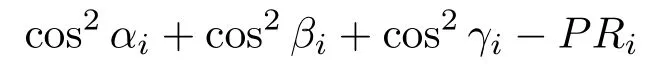
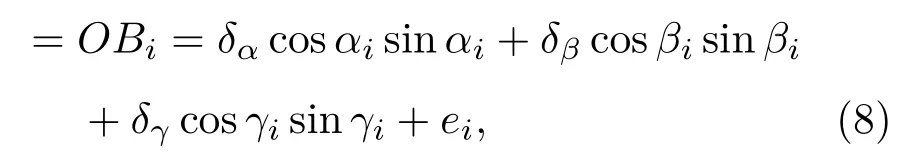
(8)式即为单次足印探测后激光指向单位向量方向余弦角中的系统误差与观测值之间的关系,式中ei为随机误差的影响项.将多次足印探测结果写成矩阵形式,即可得激光指向角系统误差校正模型为

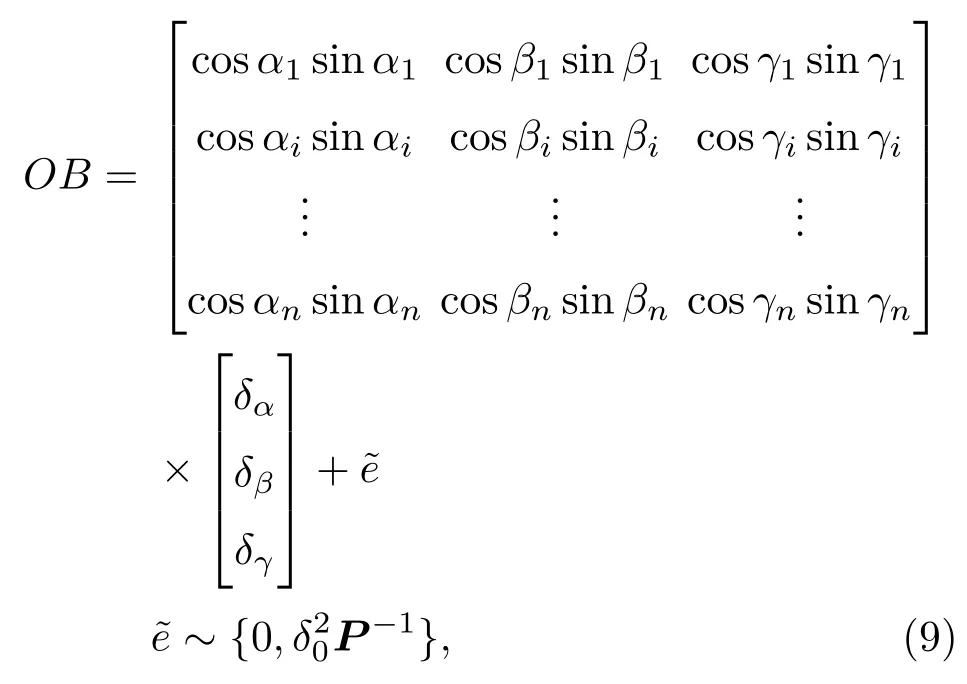
(9)式中δ0为单位权中误差,P为权矩阵.将(9)式写成观测方程形式,即OB=A∗˜ε+˜e.采用Markov估计进行解算可得激光指向向量方向余弦角中系统误差的最优估计.M arkov估计的计算方法如(10)式

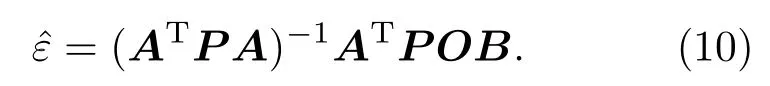
通过(10)式校正所得的激光指向向量方向余弦角中的系统误差可用于星上系统测量的激光指向单位向量校正,进一步可通过足印探测的方法对校正的结果进行检定,形成在轨校正和在轨检定的数据处理闭环,即在轨标定.式中权矩阵P具有如(11)式所示的形式[16],

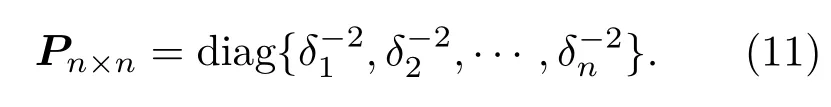
由于激光指向角系统误差校正模型对指向角误差的标定精度直接受到探测器定位的足印中心精度的影响,因此,(11)式中的对角线元素δ2由探测器对足印中心的定位精度确定.如前文所述,探测器对足印中心的定位精度受到探测器能级数和探测器布设间距的影响,不同布设间距不同能级数条件下,探测器对足印中心的提取精度如图3所示.本文仿真实验中探测器能级数已确定为8,且为了保证实验时的一致性,多次足印探测实验时探测器的布设间距为固定值,因此权矩阵P为单位矩阵.

3 实验与结果分析

星载激光测高仪通常会以近似天底的方向发射激光脉冲,相当于测高仪过境探测器布设的区域时激光以正入射的方式入射到探测器所在的阵列面,即γ角近似为零度角.通过观察激光指向角系统误差校正模型可知,若γ角近似为零度角,则(9)式中待求解未知向量的系数矩阵的三个列向量均近似为零向量,系数矩阵的条件数趋近无穷,此时方程的解不稳定.若激光以偏离天顶的方向入射到探测器所在的阵列面,即入射角γ增加,则系数矩阵的条件数减小,方程的解趋于稳定.因此,指向角系统误差校正模型的校正性能受到激光在探测器阵列面入射角的影响.由于选定的探测器布设区域不可能是绝对的平面,因此,校正模型对系统误差的反演精度同样受到标定场地表粗糙度的影响.由足印探测的在轨标定原理可知,其对指向角系统误差的在轨校正同样受到足印中心坐标定位精度的影响.而能量探测器对足印中心的定位精度受到多种因素的影响,其中主要影响因素为探测器的能级和探测器布设间距.2.1节中已确定探测器的设计能级数为8,因此探测器对足印中心的定位精度主要受探测器布设间距的影响.综上,激光指向角系统误差校正模型对系统误差的反演精度受到激光入射到探测器阵列面的入射角、标定场地表粗糙度和探测器布设间距的影响,因此,有必要对这些影响因素进行分析,从而将分析结果用于指导星载激光测高仪在轨标定实验的实施.

3.1 激光在探测器阵列面的入射角和标定场地表粗糙度

根据(9)式进行仿真实验设计,对指向角误差在轨校正模型进行评估,分析激光在探测器阵列面的入射角和标定场地表粗糙度对模型校正性能的影响.假定卫星的位置沿着某一轨迹线,且点与点之间的间距为170 m,卫星位置的不确定性分别为径向5 cm和水平向20 cm[14].同时假定探测器的布设间距为10m,结合上述足印中心提取算法的定位结果,即可计算得到激光指向方向余弦((3)式).除此之外,分别选定10组激光指向单位向量方向余弦角中的系统误差“真值”δα,δβ,δγ作为仿真实验的输入,同时在方向余弦角中加入随机误差.方向余弦角系统误差的量级一般在几十个角秒,指向角随机误差一般在1.5 arcsec[7].在仿真实验中,选定方向余弦角中系统误差的范围为10-30 arcsec.对应的就有1000种不同的激光指向单位向量方向余弦的输入系统误差组合.对每一种输入系统误差组合通过(9)式进行解算,可得系统误差δα,δβ,δγ的解算值,与输入系统误差真值进行比较,可得指向角系统误差校正模型解算值与输入系统误差真值之间的偏差,对偏差进行统计分析得到其均值和标准差,即可对校正模型的性能进行评估.选定不同的激光在探测器阵列面的入射角进行仿真实验,仿真结果如图4所示.

当激光在探测器阵列面的入射角过大时,会导致探测器的探测效率下降,且测距精度也会降低,因此选定入射角在小范围内变化(10°以内).由图4中左图可知,随着激光在探测器阵列面的入射角增加,校正模型对激光指向单位向量方向余弦γ角中系统误差的校正精度提高,当入射角为3°时,随着入射角的增加,校正精度不再有明显提高;由右图可知,激光在探测器阵列面的入射角增加对激光指向方向余弦α角和β角中系统误差的校正精度没有影响.结合校正模型((9)式)进行分析,当激光在探测器阵列面的入射角增加时,即γ角增加时,此时方程中未知向量的系数矩阵的第三个列向量会逐渐偏离零向量,因此,此列向量对应的未知项的解算精度会越高;而γ角在小角度范围内变化时,对未知向量系数矩阵的前两个列向量的影响较小,因此,对前两个列向量对应的未知项的解算精度影响不明显.综合以上分析可知,为了保证校正模型对激光指向方向余弦角中系统误差的校正精度,应使激光以3°以上的角度入射到探测器阵列面.同理,选定不同标定场地表粗糙度进行仿真实验设计,仿真结果如图5所示.

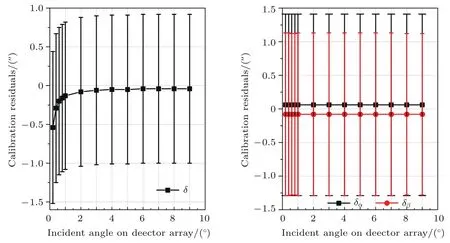
图4 (网刊彩色)校正精度受激光入射角的影响Fig.4.(color on line)Calib ration perform ance depend on laser incident angle on detector array.

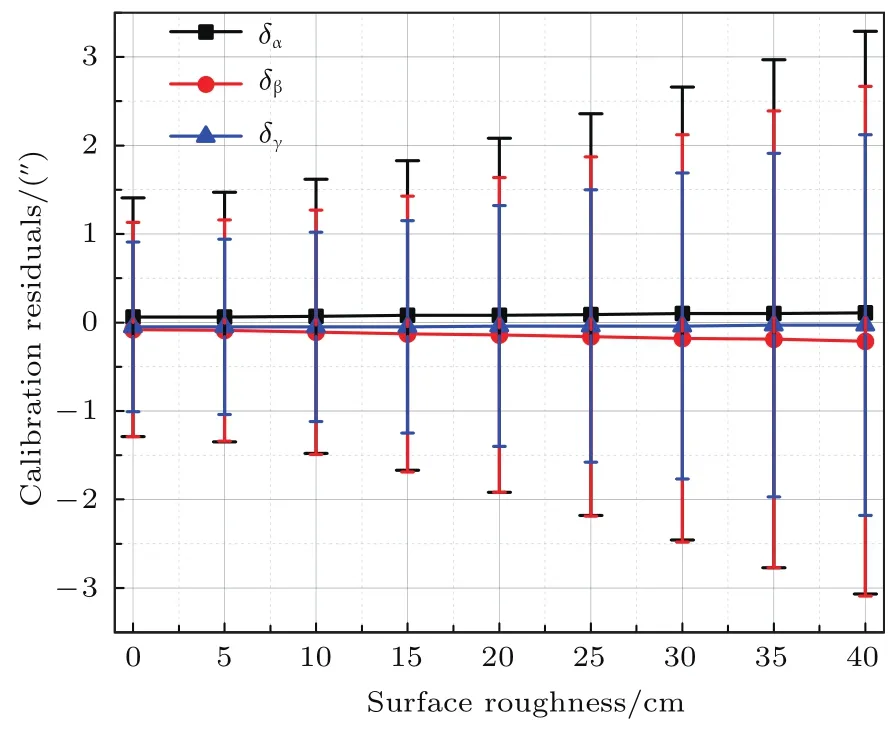
图5 (网刊彩色)校正结果受地表粗糙度的影响Fig.5.(color on line)Calib ration perform ance depend on surface roughness.

由图5可知,随着标定场地表粗糙度的增加,校正模型对激光指向方向余弦角中系统误差的校正精度下降,且校正精度与地表粗糙度之间呈现近似线性关系.由图中数据可得,若要满足1.5 arcsec的校正精度,则标定场地表粗糙度不应超过10 cm.

3.2 探测器布设间距

选定探测器能级为8后,改变探测器的布设间距并设计仿真实验,分析探测器布设间距对足印中心定位精度的影响.仿真结果如图6所示.

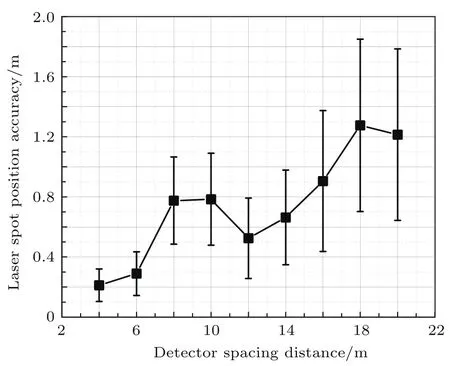
图6 不同布设间距对应光斑中心定位精度Fig.6.Footp rint geolocation accu racy under d iff erent layout spacing.

由图6可知,随着探测器布设间距的增加,探测器对足印中心的定位误差呈增加的趋势.由于足印中心提取算法的非线性性,使得图6中出现相应的抖动现象.图6中探测器布设间距在4m到20m范围内变化,对应足印中心定位精度的最大变化约为1.8m,当测高仪轨道高度为600 km时,1.8m的定位精度变化对应0.6 arcsec的激光指向检定精度变化.综合激光在探测器阵列面的入射角及标定场地表粗糙度对校正精度影响的分析结果,分别选定入射角为3°,标定场地表粗糙度为10 cm.仿真分析探测器布设间距变化对校正模型性能的影响.仿真结果如图7所示.

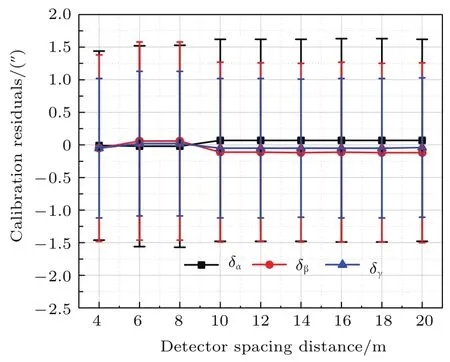
图7 (网刊彩色)校正结果受探测器布设间距的影响Fig.7.(color on line)Calib ration perform ance depend on detector spacing distance.

由图7可得,探①——校正模型对系统误差的反演精度产生一定的波动变化,且变化的范围较小,最大变化范围约为0.5 arcsec.这与图6所示的结果相符.图6中随着探测器布设间距的变化,探测器对足印中心的定位精度同样呈现出抖动现象,且定位精度最大变化约为1.8 m,对应指向角的检定精度约为0.6 arcsec.由此可知,由于测高卫星轨道高度的杠杆作用,使得探测器布设间距变化所引起的足印中心定位精度的变化,并最终反映在激光指向角检定精度变化上的影响较小.然而,同样由于测高卫星轨道高度的杠杆作用,较小的激光指向角误差会产生较大的测距误差.对应上述0.6 arcsec的激光指向检定误差会使得激光测距值产生3 cm的误差.综上,探测器的布设间距通过如下流程确定.首先,确定星载激光测高仪激光指向角误差对应的测距误差分配项,通过此测距误差分配项确定测高仪的激光指向角检定精度;其次,通过激光指向角检定精度结合测高卫星的轨道高度确定足印中心的定位精度;最后,根据足印中心定位精度的要求确定探测器的布设间距.

3.3 资源三号02星激光测高仪在轨标定实验

2016年5月30号,我国民用空间基础设施发展规划的首颗遥感业务卫星资源三号卫星02星成功发射.资源三号02星发射升空后与2012年发射的我国首颗高精度民用立体测绘卫星资源三号卫星01星形成双星组网运行,将全球覆盖的周期缩短了一半.资源三号02星相较于01星最大的特点就是其搭载了我国首个对地观测的星载激光测高试验性载荷,其不具备全波形记录的功能,从而使资源三号02星可通过主动测高的方式有效提升高程测量的精度.

2016年8月,改进设计的能量探测器在内蒙古自治区苏尼特右旗由资源三号02星搭载的激光测高仪进行在轨标定.由于资源三号02星搭载的激光测高仪是我国首个对地观测的试验性激光测高载荷,因此,这也是国内首次开展针对星载激光测高仪的在轨标定实验.标定实验时,探测器的布设间距为10 m,标定场地表粗糙度不超过10 cm.实验总共进行了三次,实验的时间依次为8月9号、8月14号、8月29号.三次实验共俘获4个足印,能量探测器都获得了有效的探测数据.对探测器的数据进行处理提取足印中心坐标,并通过校正模型对指向角系统误差进行校正,数据处理结果表明,资源三号02星上搭载的激光测高仪高程测量精度由标定前的6.3m提升到了1.6 m[17].由于资源三号02星上搭载的激光测高仪不具备全波形记录的功能,因此其测距精度不高,未来随着测距精度的提高,对于我国后续发射的带全波形记录功能的星载激光测高仪,其高程标定精度还有进一步提升的空间.

4 结 论

在轨标定为星载激光测高仪足印中心的定位精度提供保障,是星载激光测高仪测量数据进行科学应用的基础.我国计划在十三五期间发射多颗以激光测高系统为载荷的对地观测卫星,但我国卫星一般采用大平台、三轴姿态稳定系统,不具备姿态机动的能力,因此,现有的姿态机动在轨校正法不适用于我国的卫星激光测高仪.现有的足印探测法仅能用于测高仪系统误差校正结果的在轨检定,不能用于测高仪系统误差的在轨校正.本文以足印探测的在轨检定方法为基础,给出了基于指向角残差的指向角系统误差在轨校正模型,从而使得足印探测的方法可以完成系统误差在轨校正及在轨检定的数据处理闭环,实现在轨标定,避免了卫星平台姿态机动的需求.同时,对用于足印探测的能量探测器进行了改进设计,并给出了改进设计依据.基于推导的校正模型设计仿真实验,对校正模型进行评估,同时对影响模型校正精度的因素进行分析,如激光入射到探测器阵列面的入射角、标定场地表粗糙度和探测器布设间距等因素.仿真实验结果表明,推导的指向角系统误差在轨标定模型能够有效反演激光指向向量方向余弦角中的系统误差,且为了使校正模型的校正精度可靠,应使得激光入射到探测器阵列面的入射角不低于3°,标定场地表粗糙度应不大于10 cm.将改进设计的能量探测器用于我国首个对地观测的试验性星载激光测高仪的在轨标定,数据处理结果表明,测高仪的高程测量精度可由标定前的6.3 m提升到1.6 m.这对我国未来发射的带全波形记录功能的星载激光测高仪实现业务化运行具有重要参考价值.

[1]Kou T,Wang H Y,Wang F,Wu X M,Wang L,Xu Q 2015 Acta Phys.Sin.64 120601(in Chinese)[寇添,王海晏,王芳,吴学铭,王领,徐强2015物理学报64 120601]

[2]Schu tz B E 2002 GLAS Algorithm Theoretica l Basis Docum en t:Laser Footprin t Location(geolocation)and Surface Profi les(Austin:The University of Texas at Austin)p11

[3]Rim H J,Schu tz B E 2002 GLAS Algorithm Theoretical Basis Docum en t:Precision Orbit Determ ination (POD)(Austin:The University of Texas at Austin)p1

[4]M a Y,Yang F L,Y i H,Li S 2015 Infrar.Laser Eng.44 2401(in Chinese)[马跃,阳凡林,易洪,李松2015红外与激光工程44 2401]

[5]M a Y,Li S,Zhou H,Y i H 2013 Opt.Precision Eng.21 813(in Chinese)[马跃,李松,周辉,易洪2013光学精密工程21 813]

[6]Filin S 2001 Ph.D.Dissertation(Austin:The Ohio State University)

[7]Lu thcke S B,Row lands D D,M cCarthy J J,Pav lis D D, Stoneking E 2000 J.Spacecraft Rockets 37 374

[8]Schu tz B E 2001 GLAS Altimeter Post-Launch Calibration/Va lidation P lan(Austin:The University of Texas at Austin)p1

[9]Y i H,Li S,W eng Y K,M a Y 2016 J.Huazhong Univ. Sci.Tec.(Nature Science Edition)44 58(in Chinese) [易洪,李松,翁寅侃,马跃2016华中科技大学学报(自然科学版)44 58]

[10]M agruder L A,Schutz B E,Silverberg E C 2003 J. Geodesy.77 148

[11]M agruder L,Silverberg E,W ebb C,Schutz B E 2005 Geophys.Res.Lett.32 1

[12]M agruder L A,W ebb C E,U rban T J,Silverberg E C, Schu tz B E 2007 IEEE Trans.Geosci.Rem ote.45 147

[13]Jiang Y,Zhang G,Tang X,Li D 2014 IEEE Trans. Geosci.Rem ote.52 7674

[14]Lisano M E,Schu tz B E 2001 J.Geodesy.75 99

[15]M agruder L A 2001 Ph.D.D issertation(Austin:The Ohio State University)

[16]Yue M,Song L,Hong Y,X iu S L,Zhou H,T ing W C 2016 Photogramm.Eng.Rem.S.82 847

[17]Li G Y,Tang X M,Chen J Y,Gao X M,Dou X H 2016 Sem inar on Novel Optoelectronic Detection Techno logy and Application X i’an,China,Novem ber 16-18,2016 p1 (in Chinese)[李国元,唐新明,陈继溢,高小明,窦显辉2016新型光电探测技术及其应用研讨会]

(Received 8 January 2017;revised manuscript received 4 May 2017)

On-orbit calibration of satellite laser altimeters based on footprint detection∗

YiHong Li Song†Ma Yue Huang Ke Zhou Hui ShiGuang-Yuan

(School of E lectronic Inform ation,W uhan University,W uhan 430072,China)

The positioning accuracy of the footprint of a satellite laser altimeter is primarily dependent on the accuracy of its laser pointing,e.g.,a 30 arcsec pointing biasw ill induce 87m horizontal error and 1.5m vertical error when the altitude is 600 km and the laser incident angle is 1°.In order to achieve the three-dim ensional high-precision observation on the Earth surface,on-orbit calibration is needed to remove the systematic pointing biasmain ly arising from the thermal effect.The current methods of on-orbit calibration and verification for laser altimeters are the attitude m aneuvering and the footp rint detection,respectively.However,the attitudem aneuvering is not app licable to the existing satellite platform of China,which uses the large platform with a three-axis attitude stabilization system.The current footprint detection method can only achieve on-orbit verification task,i.e.,the horizontal and vertical errors can be evaluated by analyzing the captured laser footp rints but the systematic pointing bias cannot be estimated and removed.An im proved design scenario of energy detector that is used for capturing laser footp rint is given in this paper.The quantification level of the captured laser energy is equal to 8,which is bigger than that of the energy detector designed for geoscience laser altimeter systems corresponding to level 2.Benefi ting from the new design scenario,fewer detectors are needed to achieve the sam e precision when calculating the centroid geolocations of captured footprints.A new system atic m isalignm ent estim ation model in the laser direction cosines is deduced,and it is used to estim ate the system atic bias by using the detected footprints based on the Gauss-Markoff criterion.W ith the new detectors and bias estimation model,the footprint detection method now can achieve on-orbit calibration,as well as on-orbit verifi cation.According to the p resented calcu lation model,simu lation experim ents are operated to analyse three effects that m ay influence the performance of the footprint detection on-orbit calibration,i.e.,the laser incident angle on the detector array,the surface roughness of the site where detectors lay out,and the grid density of the detector array.The simu lation results indicate that,when the horizontal positioning accuracy of the captured footp rint centroid demands better than 1.8 m which corresponds to 0.6 arcsec laser pointing accuracy when the altitude of the satellite is 600 km,the grid distance of the detector array can be 20 m,the laser incident angle on the detector array shou ld be larger than 3°,and the surface roughness of the calibration site should be less than 0.1m.The designed detectors and calibration method w ill be used to capture laser footp rints and rem ove the system atic bias for the laser altimeter on China GF-7 satellite,which is one of the upcom ing high-resolution satellites for Earth observation.

satellite laser altimeter,systematic bias,on-orbit calibration,energy detector

PACS:42.62.-b,06.20.fb,85.30.-z,07.07.D f DO I:10.7498/aps.66.134206

∗对地高分辨率观测系统国家科技重大专项工程“高分遥感测绘应用示范系统(一期)”(批准号:AH1601-8)、国家自然科学基金(批准号:41506210,11574240)、测绘公益性行业科研专项经费资助项目(批准号:201512016)、中国博士后基金(批准号: 2016M 600612)和中央高校基本科研业务费专项资金(批准号:2015212020201)资助的课题.

†通信作者.E-m ail:ls@whu.edu.cn

PACS:42.62.-b,06.20.fb,85.30.-z,07.07.D f DO I:10.7498/aps.66.134206

*Pro ject supported by National Science and Technology M a jor Project,China(G rant No.AH 1601-8),National Science Foundation of China(G rant Nos.41506210,11574240),Pub lic Science and Technology Research Funds Projects of Survey, China(G rant No.201512016),China Postdoctoral Science Foundation(Grant No.2016M 500612),and the Foundm ental Research Funds for the Central University of M inistry Education of China(G rant No.2015212020201).

†Corresponding author.E-m ail:ls@whu.edu.cn