一种基于广义Duffing振子的水中弱目标检测方法∗
2017-08-07姚海洋1王海燕1张之琛1申晓红1
姚海洋1)2) 王海燕1)2)† 张之琛1)2) 申晓红1)2)
1)(海洋声学信息感知工业和信息化部重点实验室(西北工业大学),西安 710072)
2)(西北工业大学航海学院,西安 710072)
一种基于广义Duffing振子的水中弱目标检测方法∗
姚海洋1)2) 王海燕1)2)† 张之琛1)2) 申晓红1)2)
1)(海洋声学信息感知工业和信息化部重点实验室(西北工业大学),西安 710072)
2)(西北工业大学航海学院,西安 710072)
(2016年11月24日收到;2017年3月26日收到修改稿)
海洋环境中,在水下目标的线谱频率未知或者目标辐射噪声的连续谱很弱时,很难实现水中弱目标的准确检测,本文提出基于广义Duffing振子检测系统的水下目标辐射噪声检测方法.通过对传统周期扰动的Duffing振子信号检测系统的分析和推广,提出了一种可输入非周期、非平稳信号的广义Duffing振子检测系统,可检测输入的无先验信息目标信号.为实现广义Duffing振子系统运动状态的精确、有效判断,提出了一种相空间图形的离散分布列计算方法,通过类网格函数实现了利用统计复杂度对系统输出的嵌入式表征,从而实现了无先验信息时的水中弱目标的嵌入式检测.相同条件下与传统检测方法仿真对比可知,本文提出的方法可以检测到更低信噪比下的目标,并能满足水中检测实时性要求.
水中目标检测,广义Duffing振子系统,统计复杂度,相空间
1 引 言
对水中远距离弱目标的被动检测是通过提取目标(指水中机动目标,如船舶、潜艇、水下航行器等)辐射噪声中的特征来实现,目标辐射噪声频谱具有特殊的线谱和连续谱,一般通过提取线谱和连续谱特征实现目标检测.线谱是目标辐射噪声谱中的一个重要特征,李启虎等[1,2]从理论方法和数值分析角度分别探讨了自相关检测、快速傅里叶变换方法、自适应线谱增强等几种方法的优劣,相比之下分段快速傅里叶变换线谱检测具有较好的效果,且对频率漂移现象有较好的宽容性.Antoni和Hanson[3]提出利用循环频率分析方法提取线谱频率,并进行了理论推导分析.周关林等[4]研究了在海洋混响背景下利用随机共振原理检测微弱线谱的方法,仿真显示,经随机共振处理后,从信号频谱图可以清晰地看到原本非常微弱的线谱信息.基于传统Duffing振子的一系列目标辐射噪声检测方法研究结果表明,在待测线谱已知的条件下,混沌振子可以实现高斯白噪声背景下信噪比低至−25 dB的微弱线谱检测[5].以上方法均要求线谱频率等参数已知,无此先验信息时,结果会受到很大影响.丛超等[6]利用间歇Duffing混沌振子实现了线谱频率未知的目标辐射噪声微弱线谱的检测,然而其多系统搜索方式导致资源消耗巨大,难以工程实现,同时其最终基于图像变化的判别方式无法实现嵌入式表征.
连续谱是目标辐射噪声频谱的另一重要特征和组成部分,具有单独的谱峰,一般通过检测此谱峰实现检测.张晓勇和罗来源[7]从频率与能量分布的角度出发,利用瞬时频率分析方法,实现了利用舰船辐射噪声连续谱进行目标检测.然而,这种基于能量的检测方法在远距离下结果会受到较大影响.同时,海洋环境噪声也并非一般情况所假设的复高斯随机过程[8,9].
随着人们对水下目标辐射噪声的深入研究,发现目标辐射噪声中含有混沌行为.Hinich等[10]利用双谱对海洋声信号进行特征分析,证实以目标辐射噪声为主的信号中含有环境噪声所不具备的混沌分量.基于目标辐射噪声信号中的特殊混沌成分,可进行目标检测.
在水下目标的线谱频率未知或者目标辐射噪声的连续谱很弱时,上述方法很难实现对水中弱目标的检测.针对这种问题,本文通过对传统周期扰动的Duffing振子信号检测系统进行分析和推广,提出了一种可直接输入非周期、非平稳信号的广义Duffing振子检测系统,目标辐射噪声信号与其他信号输入广义Duffing振子系统后输出相空间存在明显差异.通过一种针对图形的离散分布列计算方法,实现了利用统计复杂度对相空间差异的嵌入式表征,进而实现了无目标辐射噪声线谱频率等先验信息条件下水中目标的低信噪比检测,分析了算法的实时性,得出了系统的最低检测信噪比.
2 常规检测系统与统计复杂度
2.1 Duffing振子检测系统
常规Duffing振子检测系统描述为

式中k为阻尼系数,−αx(t)+βx3(t)为非线性恢复力,rcos(ωt)为内策动力,ω为内策动力频率,r为内策动力幅值,x为振动幅值,y为振动速率.
在稳定内策动力下,取α,β,ω为常数,固定k时,随着r从0逐渐增加,系统输出相空间将依次出现:同宿轨道周期状态、分叉状态、混沌状态和大尺度周期状态.
基于Duffing振子检测系统的信号检测方法的基本思想是:将待测信号作为特定参数输入临界状态下的检测系统,利用系统所拥有的丰富的非线性动力学特点,辨识其运动状态,根据运动状态的变化,最终达到微弱信号检测的目的[11].
由以上表述可知,Duffing振子检测系统会在稳定扰动下发生规律变化.那么,将待测信号以加项形式输入(1)式表征的系统,待测信号中的成分构成决定了系统输出相空间的形态,一般的周期信号(如单频信号等)和随机信号(如高斯白噪声信号、色噪声信号)输入系统总会围绕上述四种状态运动.前期研究表明,特定的复杂待测信号会使得输出相空间脱离以上四种标准形态,本文据此进行目标信号的检测.
2.2 统计复杂度
以输出相空间形态变化为依据进行系统运动状态判断,为实现运动状态判断的嵌入式表述,引入以下统计复杂度的概念.统计复杂度是刻画与系统时间信号相关联的概率分布的函数,通过标准Shannon熵和失衡度表示[12].
Shannon熵是经典信息论中的测度,表示概率分布为P={pi,i=1,···,N}的物理过程的不确定程度:
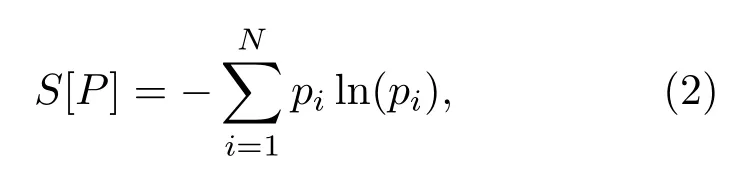
其中,pi为概率值,N为随机变量个数.
系统处于完全随机状态,即概率分布为均匀分布Pe={1/N,···,1/N}时,Shannon熵的值达到最大S[Pe]=lnN.由此,标准Shannon熵为
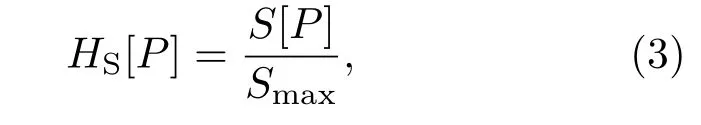
其中Smax=S[Pe]=lnN,显然,0 6 HS[P]6 1.
失衡度K用于度量系统任一状态T时的概率分布P与均匀分布Pe之间的距离DS,表示为
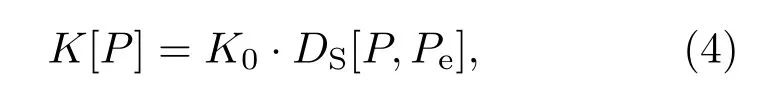
其中K0是归一化常数,则0 6 K 6 1.DS通常选用Jensen-Shannon散度JS进行刻画,对于概率空间中任意两个分布P1和P2,其表示为

那么,失衡度为
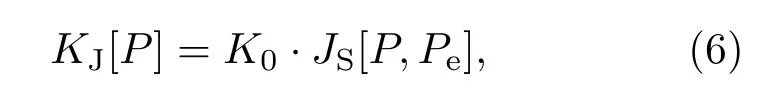
其中,归一化常数K0为JS[P,Pe]取最大值时的倒数.
由(3)式所示的标准Shannon熵和(6)式所示的失衡度,可得下述统计复杂度:
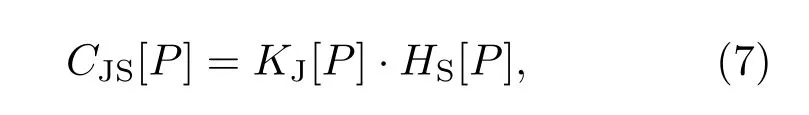
其中P为样本概率分布.
由于标准Shannon熵反映系统的无序性,失衡度描述系统时间信号在概率空间中的结构特性,故(7)式表示的统计复杂度同时反映了系统的这两种性质,其计算关键是找出信号的概率分布P.在计算输出相空间的统计复杂度后,根据相空间的有界性和差异性,提出一种针对图形的离散分布列计算方法.
3 广义Duffing振子检测系统
由于目标辐射噪声为非周期、非平稳信号[13],而常规Duffing振子检测系统输入为周期或平稳随机信号.本文将常规Duffing振子检测系统进行推广,称非周期、非平稳信号输入下的Duffing振子检测系统为广义系统.
将待测信号以加项形式输入到(1)式表示的检测系统,描述为
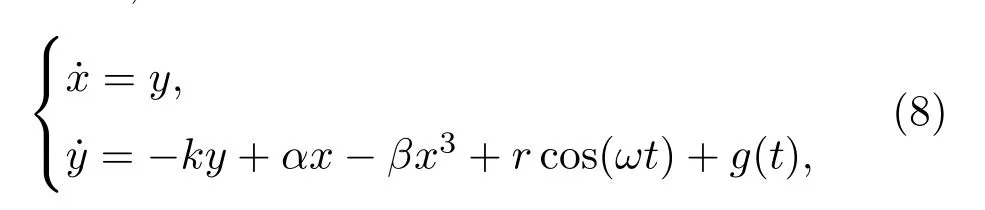
其中g(t)=Acos(ω′t+ φ)+n′(t),n′(t)为高斯白噪声信号,A为目标信号幅值,ω′为目标信号频率,φ为目标信号相位.(8)式表示传统周期扰动下的常规Duffing振子检测系统.
设目标辐射噪声信号为s(t),海洋环境噪声为n(t),检测系统的输入信号(即待测信号)可表示为
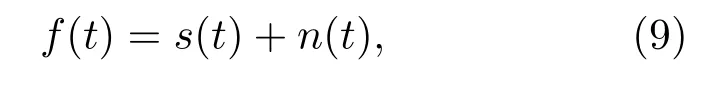
显然,(9)式表示非周期、非平稳信号.
根据(8)式,对此周期信号扰动的检测系统进行推广,将(9)式代入以代替g(t),得到
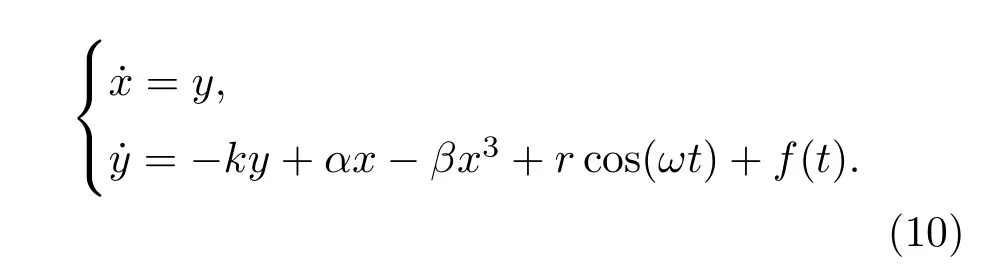
由于(8)式所示系统的检测原理为对周期信号敏感和对平稳噪声信号免疫,当输入非周期、非平稳信号时,其原本具有的一些特殊的性质和限制将发生改变.下面以系统(8)为出发点,分情况讨论推广系统(10)的性质和可行性.
情况1当f(t)=g(t)时,即(10)式表示的检测系统等价于(8)式表示的系统,其特性分析如下.
为了能检测到更低幅值的单频信号,参数r的取值需尽可能精确.采用定步长四阶龙格-库塔方法进行数值计算,步长设定为0.001,取k=0.5,α =1,β =1,ω =1,初值为(1,1). 利用Melnikov方法[14]计算得知,r=0.863时,(1)式所示的Duffing振子系统处于混沌临界状态,分别取不同精度r值,r=0.8,0.86,0.863,得到临界状态系统相空间形态,如图1所示.
由图1所示的系统临界状态相空间形态可以看出,内策动力幅值r取值越精确,相空间显示出的混沌形态越不明显,越趋于大尺度周期状态.在r=0.8和0.863两种参数时分别输入单频信号、高斯白噪声信号及单频+高斯白噪声信号三种情况下的系统相空间如图2和图3所示.由图3(b)和图3(c)可以看出,单频信号加背景噪声的输入系统状态判断非常困难.且由仿真及文献[14]可得结论1:Duffing振子检测系统对高斯白噪声和色噪声信号免疫,仅使得相空间曲线变得不光滑.
仿真结果表明,周期信号加平稳噪声输入下的Duffing振子检测系统存在以下问题:

图1 临界状态下不同内策动力幅值相空间 (a)r=0.8;(b)r=0.86;(c)r=0.863Fig.1.Output phase spaces under critical state with di ff erent amplitude of policy dynamic:(a)r=0.8;(b)r=0.86;(c)r=0.863.
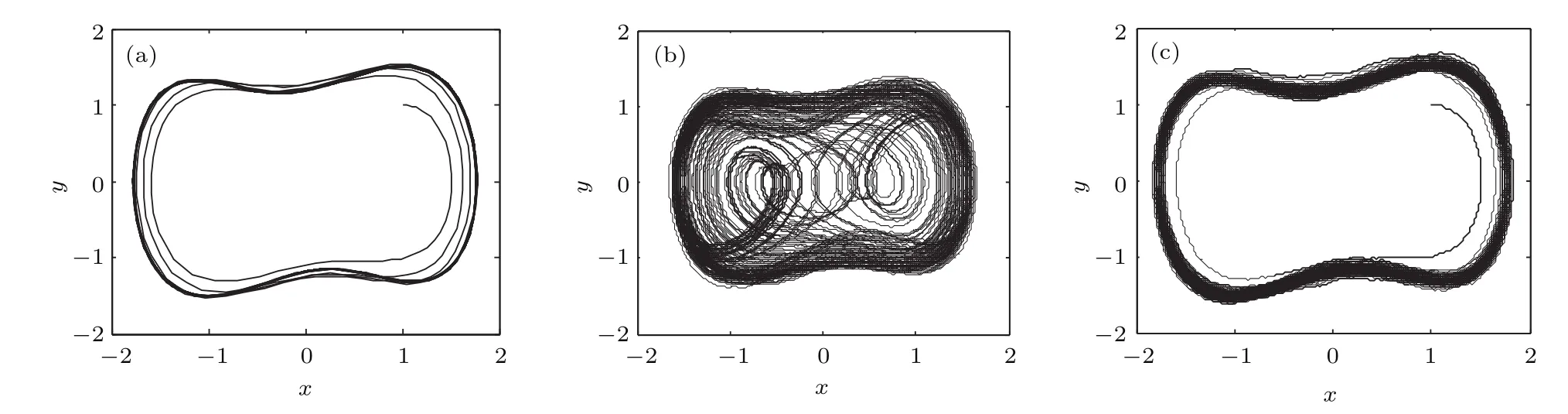
图2 内策动力幅值r=0.8时检测过程相空间 (a)输入单频信号;(b)输入高斯白噪声信号;(c)输入单频信号+高斯白噪声信号Fig.2.Output phase spaces in detection when r=0.8:(a)Single-frequency signal;(b)white Gaussian noise signal;(c)single-frequency signal+white Gaussian noise signal.

图3 参数r=0.863时检测过程相空间 (a)输入单频信号;(b)输入高斯白噪声信号;(c)输入单频信号+高斯白噪声信号Fig.3.Output phase spaces in detection when r=0.863:(a)Single-frequency signal;(b)white Gaussian noise signal;(c)single-frequency signal+white Gaussian noise signal.
1)低信噪比下,对参数r取值越精确系统输出相空间差异越不明显,判断系统运动状态越困难;
2)系统(8)进行单频信号检测时,需满足内策动力rcos(ωt)的频率ω与待测信号g(t)=Acos(ω′t+ φ)+n′(t)的频率ω′很接近,即

其中ε为常数,|ε|<0.03ω;
3)待测信号g(t)需要与内策动力进行相位同步,形成正激励;
4)低信噪比下,随着随机噪声的方差变大,通过输出相空间清晰地进行运动状态判断,定步长四阶龙格-库塔方法的步长需变小,计算量大大增加,检测系统的实时性变差.
以上四个问题为(8)式表示的Duffing振子检测系统所固有的困难,下面将会讨论广义Duffing振子系统是否存在这些问题.
情况2当f(t)=s(t)+n(t)时,(10)式表示广义Duffing振子检测系统,其特性分析如下.
由结论1可知,高斯白噪声和色噪声对相空间形态无影响,于是,令输入为f(t)=s(t).为方便观察,取r=0.8,使得系统进入混沌临界状态,如图1(a)所示.
混沌信号为一类具有代表性的非周期、非平稳信号,对输入混沌信号时的广义Duffing振子检测系统的性质进行分析.令s(t)为混沌特性信号,利用奇异吸引子产生混沌特性信号,Lorenz吸引子表示为[15]

取初值(x0,y0,z0)=(0,0,10−10);σ,b,c均为常系数,σ=10,b=−8/3,c=28.利用定步长四阶龙格-库塔方法进行计算,取步长为0.001,得到Lorenz吸引子信号W=(x,y,z),其中x,y,z均为一维向量.
由于Duffing振子输入初值不能为零,取sL(t)=z,令f(t)=sL(t).同时,为观察改变输入信号相位时系统输出相空间的变化,对输入信号进行平移.分别输入

其中m为远小于n的整数.广义Duffing振子系统输出相空间形态如图4所示.

图4 输入Lorenz信号后系统输出相空间 (a)相空间1;(b)相空间2Fig.4.Output phase spaces when the input is Lorenz signal:(a)Phase space one;(b)phase space two.
输入不同相位的Lorenz信号,广义Duffing振子系统输出相空间具有两种形态:一种是相空间内部向焦点运动轨迹发生变化,如图4(a)所示;另一种是相空间左右鞍点轨道数比重发生变化,如图4(b)所示.两种相空间形态无固定规律,系统运动状态没有发生变化,仍为混沌状态.同时,将2倍、1.5倍、1/2、1/10的原信号能量的信号输入,得到的相空间依然如图4所示.于是得到结论2:Lorenz吸引子产生的混沌特性信号输入广义Du ffing振子系统时,相空间形态变化,系统运动状态不发生改变,且不受能量变化影响.
推广结论2到任意混沌信号,分别考察与Lorenz系统相空间运动方式不同的Henon吸引子[16]和与Lorenz系统不拓扑等价的Chen吸引子[17]产生的信号输入广义Duffing振子系统时输出相空间的变化.仿真显示,Henon吸引子信号和Chen吸引子信号输入广义Duffing系统后,输出相空间与如图4所示的Lorenz吸引子信号的输出相空间形态相似,仅左右鞍点轨道占比不同.
故而,非平稳的混沌特性信号输入广义Du ffing振子系统可以得到有效的相空间输出,且可能会使得左右鞍点轨道运动发生变化,系统运动状态不变.
情况3当f(t)=s(t)+n(t)时,(10)式表示广义Duffing振子检测系统,为了解更加复杂的非周期、非平稳信号输入系统后的运动状态变化,设计以下四种输入形式:
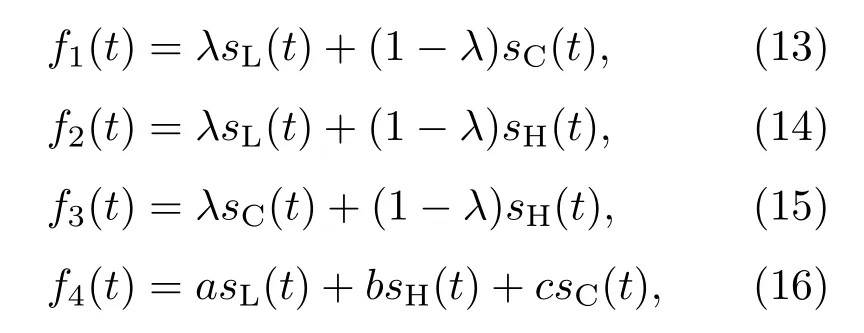
其中sL(t),sH(t),sC(t)分别表示Lorenz吸引子信号、Henon吸引子信号和Chen吸引子信号;λ,a,b,c为常数,0 6 λ 6 1,a+b+c=1.此种情况下输出相空间形态依然如图4所示.
情况4当f(t)=s(t)+n(t)时,(10)式表示广义Duffing振子检测系统,综合分析如下.
若输入信号同时含有单频信号、混沌特性信号和随机噪声信号,即

其 中s1(t)= Acos(ωt);s2(t)为 形 式 如(13)—(16)式的混沌特性信号;s3(t)为随机噪声信号;,,是值为0或1的常数, 且,不同时为零.此种情况下输出相空间形态依然如图4所示,若存在s3(t)则会使得相空间变得粗糙.
因此,非周期、非平稳信号输入广义Duffing振子检测系统可以得到有效相空间输出,并且对临界状态下的系统运动状态没有产生如单频信号的扰动.
综合以上分析可知,改变输入信号组成模式有可能使得相空间形态发生一些改变,但一般的加性非周期、非平稳信号不会对运动状态产生影响.试验证明,目标辐射噪声输入系统时,会产生如图5所示的特殊输出相空间,依据如图1(a)、图4所示相空间与如图5所示相空间差异可实现目标检测.

图5 特殊输出相空间 (a)相空间1;(b)相空间2Fig.5.Special output phase spaces:(a)Phase space one;(b)phase space two.
非周期、非平稳信号输入广义Duffing振子系统时,情况1中所述常规系统(8)存在的四种问题均可进行推广.
1)相空间形态发生巨大变化,不再是密闭的椭圆形态,更易判断系统运动状态,且由于不涉及单频扰动,检测精度与参数r设置无关,而取决于系统对目标信号复杂度的敏感度,可设临界参数为r=0.8.
2)输入信号改变,广义Duffing振子系统相空间变化主要依赖于输入信号中的复杂的非线性成分,故而不存在频率接近的问题.
3)输入信号发生变化,无需使得输入信号对策动力产生正激励,故而无需进行相位同步.
4)检测系统的实时性将在下面一节给出.
综上所述,广义Duffing振子系统是可行的,并且可以实现对水下目标辐射噪声的有效检测.
4 相图离散分布列计算方法
为实现嵌入式检测,需借助2.2节中所述的统计复杂度,计算系统输出的统计复杂度需要得到输出时间序列的概率分布.从已知时间信号中提取概率分布的一种有效方法为Bandt-Pompe算法[18],然而Bandt-Pompe算法针对时间序列进行重排列时,由于嵌入维数DM是确定的,无法灵活调整计算精度,一些情况下过于精确的计算会使得实时性降低,影响检测性能.
本文直接针对输出相空间提出一种基于类网格函数的相图离散分布列计算方法,可达到相空间离散分布列提取的目的,并可以通过控制类网格函数进行精度控制.
通过搜索检测系统输出(x,y),分别得到x的最大值xmax与最小值xmin,y的最大值ymax与最小值ymin,则

其中xscale为相空间x轴方向上的相图范围,yscale为相空间y轴方向上的相图范围.
根据(18)和(19)式可计算输出相空间的网格步长:
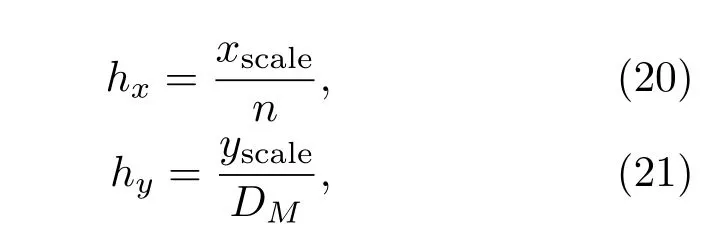
其中hx为x轴上的步长,hy为y轴上的步长,n为精度控制参数即x轴划分网格数,DM为重构维数(Duffing振子重构维数为2).
由(20)和(21)式所示步长,分别以x=xmin,y=ymin为初值,可得到以下分段区间:
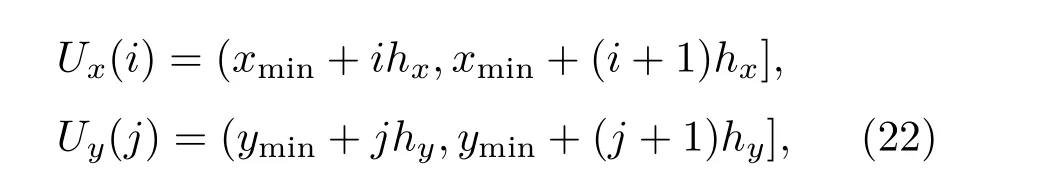
其中i=0,···,n − 1;j=0,···,DM− 1.
本文对类网格函数定义为
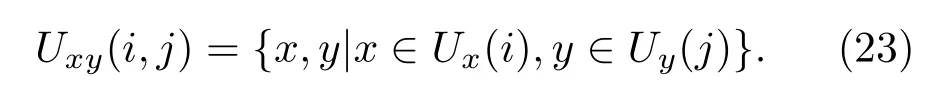
根据本文研究的非周期、非平稳信号的相空间特性,建立基于类网格函数的输出相空间图形的分布列计算公式:
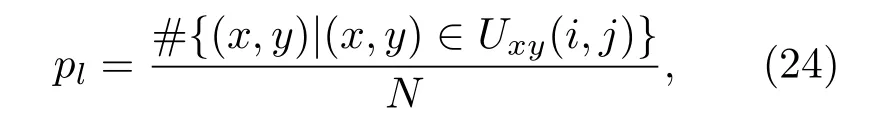
其中pl为时间序列的分布列,#表示{}中对应数对的数量,N为数对(x,y)的总个数,l=1,···,n × DM.
依据概率统计理论,显然,该算法需满足n×DM≪N,利用Grassberger-Procaccia(G-P)算法[19]得到嵌入维数DM.由于引入了嵌入维数DM,本方法也适用于其他类型的混沌系统输出分布列计算.
本方法利用类网格函数,推导出了输出相空间图形的分布列计算公式,可计算出系统输出相空间图形的离散分布列,其中n的取值决定了分布的准确性,取值越大,划分的网格越多,越接近真实分布.进而可以计算出Shannon熵和统计复杂度,对系统输出相空间进行量化描述,实现了目标的嵌入式检测.
5 实验验证
5.1 检测方法海上实验分析
为了验证以上检测方法的可行性,以四种舰船作为目标(记为1—4型目标),1型和2型为以不同航速航行的300吨级舰船,3型和4型为同航速3000吨级和万吨级舰船,声呐收集信号时的采样频率fs为48000 Hz,降采样获取100—8000 Hz的目标辐射噪声,样本长度N=5000,1型舰船辐射噪声时域波形如图6所示.将信号归一化,记为sJ(t),分别取

即将信号进行连续三点平移(取n=5000,即截取t=n/fs=0.104 s长度的信号),得到的平移后的信号分别输入(10)式所示的广义Duffing振子检测系统,得到目标存在时广义Duffing振子检测系统输出相空间形态如图7所示(仅显示1型辐射噪声输出形态).

图6 1型舰船辐射噪声时域形态Fig.6.Time domain waveform of ship-radiated signal type one.
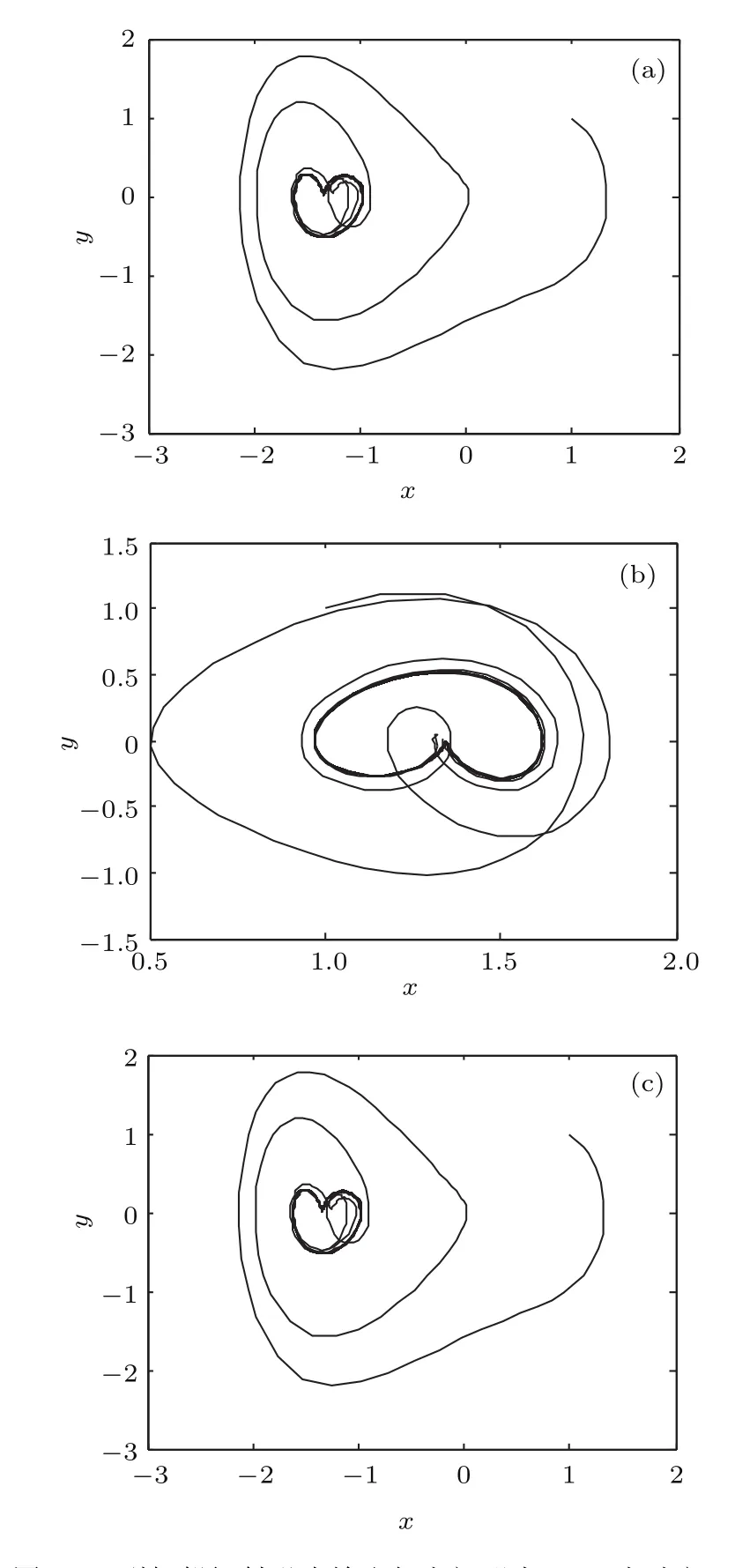
图7 1型舰船辐射噪声输出相空间形态 (a)相空间1;(b)相空间2;(c)相空间3Fig.7. Output phase spaces when the input is ship-radiated signal type one:(a)Phase space one;(b)phase space two;(c)phase space three.
其他三种舰船的输出相空间也均为如图7所示的特殊形态,只是两种特殊形态出现的次数和排列顺序不同.
由以上广义Duffing振子系统输出相空间可知,连续相移的舰船辐射噪声信号输入后,所有输出相空间均呈特殊形态.为增加检测准确性,本文采用连续三点相移输入的策略进行目标检测.
一定范围(方圆5 km)内无目标经过时,采集到如图8所示的未经归一化的海洋环境噪声时域波形.
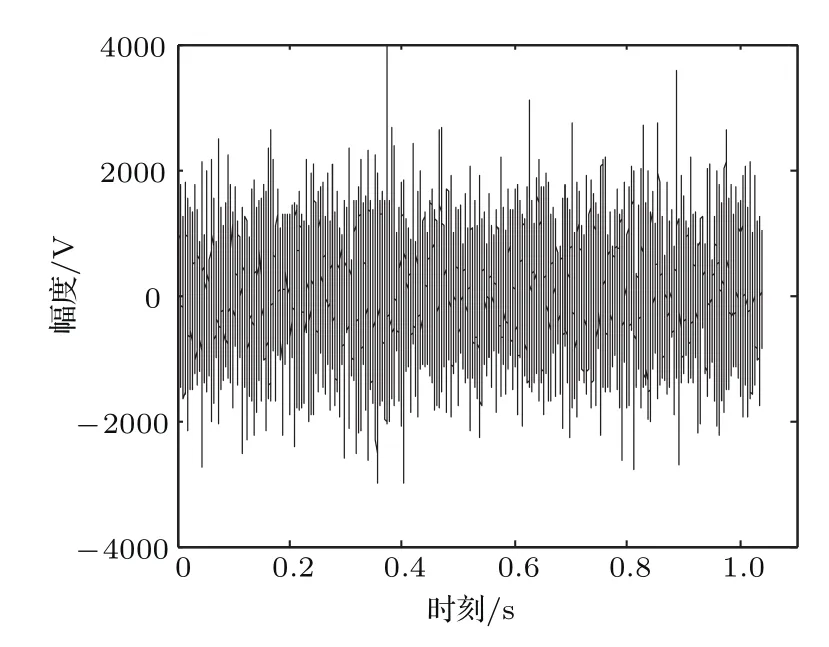
图8 海洋环境噪声时域波形Fig.8.Time domain waveform of ocean ambient noise.
海洋环境噪声输入后的系统输出相空间如图9所示.
由图9可知,此段海洋环境噪声信号输入广义Duffing振子检测系统之后,不改变系统运动状态,仅对左右鞍点运动偏重有影响.同时,在后续仿真中,设计如下试验:
试验1输入2倍、1.5倍、1/2、1/10的原海洋环境噪声能量的信号;
试验2取原海洋环境噪声信号中不同时段部分分别输入;
试验3对其他海域3—5级海况下收集到的环境噪声数据分别做如试验1和2的处理.
上述三种试验均得到类似图9所示的相空间形态,只是左右鞍点运动高度略有差别.
从以上结果可知,利用这种相空间形态的区别进行海洋环境噪声背景下舰船辐射噪声的检测具有一定的普适性.
根据2.2节所述过程及第4节的算法,可得到如图1(a)所示的混沌临界状态和如图2(a)所示的大尺度周期状态相空间形态的统计复杂度.由G-P算法[19]得到Duffing振子重构维数为2,即DM=2,取精度参数n=5,即将相空间分割为2×5的小块(有限个数分割的前提下,均为离散型随机变量,分割块数越多,对应的分布越精确,分割块数为无穷时,得到概率密度曲线).进一步得到图1(a)和图2(a)对应的分布列.根据表1和表2所列分布列,由2.2节可得混沌临界状态统计复杂度为0.0169,大尺度周期状态统计复杂度为0.0349.
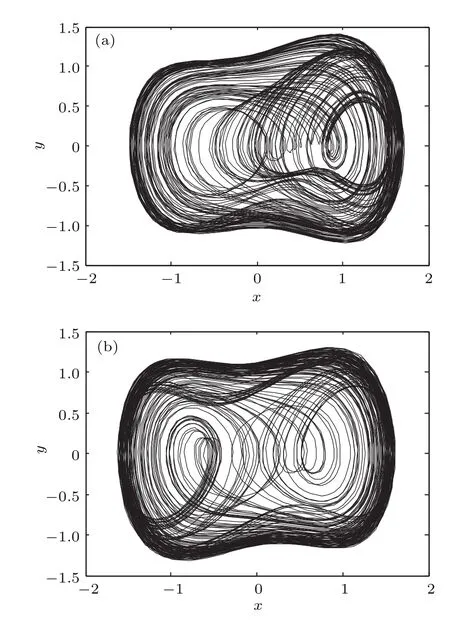
图9 海洋环境噪声输入时系统输出相空间 (a)相空间1;(b)相空间2Fig.9.Output phase spaces when the input is ocean ambient noise:(a)Phase space one;(b)phase space two.

表1 混沌临界状态相空间分布列Table 1.Phase space distribution sequence in the chaotic critical state.

表2 大尺度周期状态相空间分布列Table 2.Phase space distribution sequence in the large-scale periodic state.

表3 特殊相空间1分布列Table 3.Phase space distribution sequence of special phase space type one.

表4 特殊相空间2分布列Table 4.Phase space distribution sequence of special phase space type two.
同理可得出图7所示的两种特殊形态相空间的分布列.根据表3和表4所列分布列,可得两种分布的统计复杂度分别为0.1907和0.2800.
由以上计算可知,特殊相空间统计复杂度值与常规相空间值差别较大,将阈值定为0.05,得到输入不同信号时的检测效果示意,如图10所示.

图10 目标检测效果Fig.10.Results of target detection.
图10中,虚线为阈值大小,圈为检测值即统计复杂度值.图中1,2检测点系统处于临界状态为检测准备时刻;3—5检测点为第一个检测时段,第3检测点存在单频干扰信号进入系统,使得系统进入了大尺度周期状态且于第5检测点干扰消失(此处假设单频信号内策动力同步等理想情况,否则依然为混沌状态);6,7检测点为检测间隔时段(同11,12与16,17),可调节;8—10检测点为第二个检测时段,检测结果为存在目标;13—15时刻为第三个检测时段,检测结果为存在目标;18—20时刻为第四个检测时段,检测结果为无目标.
由1—4型目标辐射噪声特殊输出相空间可以看出,不同目标辐射噪声两种特殊输出相空间排列次序不同、出现次数不同,由于两种特殊相空间统计复杂度值不一样,导致检测点起伏变化不同,通过增加输入信号平移次数,突出这种区别,可实现目标识别.
5.2 检测性能分析
根据以下信噪比的计算公式,可得利用广义Duffing振子检测目标辐射噪声的最低检测信噪比:

其中Psignal为信号的平均功率,Pnoise为噪声的平均功率.当舰船辐射噪声信号能量过低时,将无法对广义Duffing振子系统形成扰动,产生如图7所示的特殊相空间,按(25)式可得到最低检测信噪比为−9.133 dB.考虑到Duffing振子检测系统对高斯白噪声的免疫性,若将海洋环境噪声假定为高斯白噪声,则基于广义Duffing振子系统的检测方法可得到最低检测信噪比为−27.55 dB.由于本文提出的方法并非以统计理论为基础得出的,故而无法得出在不同虚警概率下的检测概率曲线.
利用能量方法,依据奈曼-皮尔逊准则,分别取虚警概率Pf为0.1,0.01,0.001,0.0001时,得到其检测概率与信噪比关系如图11所示.由计算可知,能量检测在虚警概率0.1、检测概率PD>98%时,检测信噪比为−11 dB左右.
在高斯白噪声背景下基于广义Duffing振子系统的最低检测信噪比(−27.55 dB)远低于能量检测的信噪比(−11 dB).然而,由于四阶龙格-库塔方法的计算方式等的影响,广义Duffing振子检测方法并非很好地适用于背景噪声为高斯白噪声的情况,而更适用于上述海洋环境噪声下的目标检测.

图11 (网刊彩色)能量检测方法检测概率曲线Fig.11.(color online)Detection probability curves of energy detection method.
需要说明的是,声纳接收到的目标辐射噪声是宽带信号,且含有海洋环境噪声成分,故而实际最低检测信噪比通过实验计算得到的还要低一些.
下面分析广义Duffing振子检测方法的实时性.上述方法主要涉及的计算包括归一化、四阶龙格-库塔方法解广义Duffing振子方程、相图离散分布列方法和统计复杂度的计算.其中,归一化和统计复杂度涉及简单的乘法和除法,相图离散分布列方法主要为分段、搜索和除法,而龙格-库塔方法比较复杂,占据了主要的运算时间.将实时性以运算时间衡量,分别输入样本点数为3000—5000时,运算量如表5所列.
计算机配置不同、数据不同等会得到不同的运算时间,因而仅利用表5观察实时性趋势.首先,由表5可以看出总体耗时均在10 s以下,对于水中目标航行速度不可能高的实际情况,算法耗时基本达到水中检测的实时性要求.其次,输入信号点数对耗时没有很大影响,主要取决于龙格-库塔方法步长的选择,考虑到相空间的完整性,选取步长为0.001.最后,表5也验证了广义Duffing振子方法的计算量主要集中于龙格-库塔方法.
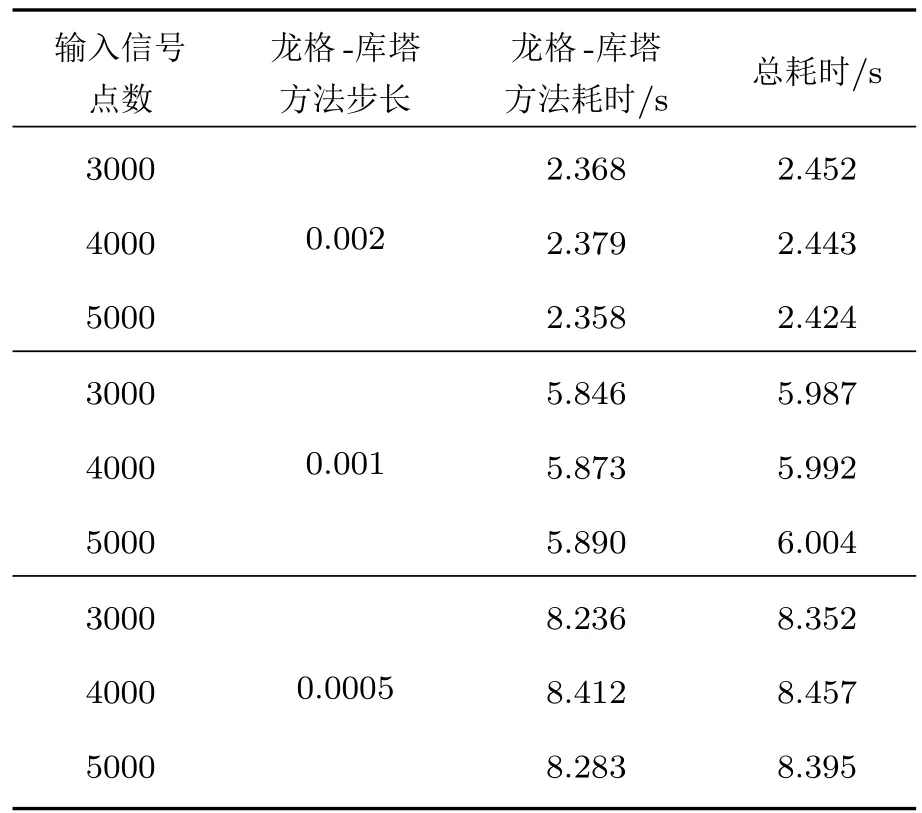
表5 广义Duffing振子检测方法实时性Table 5.Real-time analysis of generalized Duffing oscillation detection method.
6 结 论
本文提出了一种基于广义Duffing振子检测系统的真实海洋环境噪声背景下目标辐射噪声检测方法,利用相图离散分布列方法计算统计复杂度对相空间进行表征,实现了线谱频率未知或者目标辐射噪声的连续谱很弱时的目标检测,给出了检测系统的最低检测信噪比,算法的实时性可满足实际要求.与常规能量方法对比可知,广义Duffing振子检测方法可以检测到更低信噪比下的目标辐射噪声信号.本文方法的特点如下:
1)通过对传统周期扰动的Duffing振子信号检测系统进行分析和推广,提出一种针对非周期、非平稳输入的广义Duffing振子检测系统,可将无先验信息的复杂接收信号直接输入系统;
2)发现了一种目标辐射噪声输入广义Duffing振子系统后的特殊形态相空间,并分析了不同信号输入后的相空间差异,通过表征特殊相空间和一般相空间差异可实现目标检测和识别;
3)提出了一种相空间图形的离散分布列计算方法,利用类网格函数推导出了相空间分布列计算公式,得到了系统输出相空间的分布列,实现了利用统计复杂度对相空间的嵌入式表征,从而实现了水下真实环境下线谱频率未知或者接收的目标辐射信号的连续谱很弱时目标的嵌入式检测.
[1]Li Q H,Li M,Yang X T 2008 Acta Acoust.33 193(in Chinese)[李启虎,李敏,杨秀庭 2008声学学报 33 193]
[2]Li Q H,Li M,Yang X T 2008 Acta Acoust.33 289(in Chinese)[李启虎,李敏,杨秀庭 2008声学学报 33 289]
[3]Antoni J,Hanson D 2012 IEEE J.Ocean.Eng.37 478
[4]Zhou G L,Li G H,Cheng J 2009 Comput.Simulat.7 337(in Chinese)[周关林,李钢虎,成静 2009计算机仿真7 337]
[5]Liu H B,Wu D W,Jin W,Wang Y Q 2013 Acta Phys.Sin.62 050501(in Chinese)[刘海波,吴德伟,金伟,王永庆2013物理学报62 050501]
[6]Cong C,Li X K,Song Y 2014 Acta Phys.Sin.63 064301(in Chinese)[丛超,李秀坤,宋扬 2014物理学报63 064301]
[7]Zhang X Y,Luo L Y 2015 Acta Acoust.40 511(in Chinese)[张晓勇,罗来源 2015声学学报 40 511]
[8]Kedar S 2011 Comptes Rendus Geosci.343 548
[9]Cato D H 2012 AIP Conf.Proc.1495 242
[10]Hinich M J,Marandino D,Sullivan E J 1989 J.Acoust.Soc.Am.85 1512
[11]Lai Z H,Leng Y G,Sun J Q,Fan S B 2012 Acta Phys.Sin.61 050503(in Chinese)[赖志慧,冷永刚,孙建桥,范胜波2012物理学报61 050503]
[12]He M J,Xu W,Sun Z K 2014 Sci.Sin.:Phys.Mech.Astron.44 981(in Chinese)[何美娟,徐伟,孙中奎 2014中国科学:物理学力学天文学44 981]
[13]Bao F,Li C,Wang X,Wang Q,Du S 2010 J.Acoust.Soc.Am.128 206
[14]Li Y,Shi Y W,Ma H T,Yang B J 2004 Acta Electron.Sin.32 87(in Chinese)[李月,石要武,马海涛,杨宝俊2004电子学报32 87]
[15]Lorenz E N 1995 The Essence of Chaos(Seattle:University of Washington Press)p186
[16]Chen G,Lai D 1998 Int.J.Bifurcat.Chaos 8 1585
[17]Xue Y J,Yang S Y 2003 Chaos Soliton.Fract.17 717
[18]Bandt C,Pompe B 2002 Phys.Rev.Lett.88 174102
[19]Grassberger P,Procaccia I 2004 The Theory of Chaotic Attractors(New York:Springer)pp189–208
PACS:43.60.–c,05.45.–aDOI:10.7498/aps.66.124302
A method of detecting underwater weak target based on generalized Duffing oscillator∗
Yao Hai-Yang1)2)Wang Hai-Yan1)2)†Zhang Zhi-Chen1)2)Shen Xiao-Hong1)2)
1)(Key Laboratory of Ocean Acoustics and Sensing(Northwestern Polytechnical University),Ministry of Industry and Information Technology,Xi’an 710072,China)
2)(School of Marine Science and Technology,Northwestern Polytechnical University,Xi’an 710072,China)
24 November 2016;revised manuscript
26 March 2017)
In the marine environment,when the line spectra of underwater target radiated signal are unknown or the continuous spectra are weak,it is extremely hard to accurately detect the underwater weak target.The line spectrum based method commonly requires spectrum information for detection,and the continuous spectrum based energy method is hard to achieve accurate detection in long distance.In this paper,an underwater radiated noise detection method based on generalized Duffing oscillator detection system is proposed.Firstly,a generalized Duffing oscillator detection system for non-periodic and non-stationary input signal is proposed through deducing the traditional Duffing oscillator detection system that is perturbed by periodic signal.And the proposed generalized Duffing oscillator detection system is able to detect the signals of targets without needing prior information.Secondly,when the target radiated signal(nonperiodic and non-stationary signal)is input into the generalized Duffing oscillator,a special form of output phase space(a special state of motion)is discovered and the di ff erences in output phase space among di ff erent input signals(periodic stationary signals,nonperiodic non-stationary signals and the target radiated signals)are analyzed.It is found that the special phase space has di ff erent form from the output phase spaces of other kinds of signals;accordingly the underwater targets can be detected through the representation of the di ff erence between special phase space and ordinary phase space.Thirdly,a discrete distribution sequence calculation method based on phase space is proposed for the precise and efficient judgment of system motion.The proposed calculation method de fi nes a similar-grid function,based on which,the distribution sequence calculation method of output phase space is deduced,and the distribution sequences of di ff erent kinds of output phase spaces are calculated.The method realizes an embedded expression of system output by using the statistical complexity,therefore achieving the embedded underwater target detection when the line spectra of underwater target radiated signal are unknown or the continuous spectra are weak.The analysis result indicates that the method is of low-computation.Finally,the experimental results in the sea are described and the lowest signalto-noise ratio(SNR)of the method is calculated to be−9.133 dB.Simulation and experimental results have shown that the proposed method can detect target successfully in a lower SNR than traditional detection method,and the real-time performance can meet the demand for underwater detection.The method in this paper provides new ideas and ways of thinking for underwater target detection,and has very important reference value for low SNR long-distance target detection under real condition.
underwater target detection,generalized Duffing oscillator system,statistical complexity,phase space
10.7498/aps.66.124302
∗国家自然科学基金(批准号:61571365)资助的课题.
†通信作者.E-mail:hyang@mail.nwpu.edu.cn
©2017中国物理学会Chinese Physical Society
http://wulixb.iphy.ac.cn
*Project supported by the National Natural Science Foundation of China(Grant No.61571365).
†Corresponding author.E-mail:hyang@mail.nwpu.edu.cn
